2D／3D图像配准中的相似性测度和优化算法

张 冉，王 雷，夏 威，高 欣

（1.中国科学院长春光学精密机械与物理研究所，吉林长春130033；2.中国科学院苏州生物医学工程技术研究所医学影像室，江苏苏州215163；3.中国科学院大学，北京100049）

2D／3D图像配准中的相似性测度和优化算法

张 冉1，2，3，王 雷1，2，3，夏 威1，2，3，高 欣2

（1.中国科学院长春光学精密机械与物理研究所，吉林长春130033；2.中国科学院苏州生物医学工程技术研究所医学影像室，江苏苏州215163；3.中国科学院大学，北京100049）

在手术引导治疗中，2D／3D图像配准能辅助医生准确定位病人病灶，而准确的配准涉及相似性测度和优化算法等众多方面。为了研究相似性测度和优化算法对2D／3D图像刚性配准的影响，本文结合6种相似性测度和4种优化方法在配准“金标准”数据上进行了2D／3D图像配准实验，并从配准成功率、平均迭代次数和平均配准时间三个方面对配准结果进行了对比研究。实验结果表明，以模式强度为相似性测度，用Powell方法进行优化搜索是最佳配准组合。并且，在不改变相似性测度条件下，Powell方法是所用优化方法中配准效果最好的优化方法。

2D／3D图像配准；刚性配准；相似性测度；优化方法；配准评估

1 引 言

在手术引导治疗中，2D／3D图像配准在辅助医生准确定位病人病灶上是一种重要技术［1－3］，被广泛的应用在图像引导的微创手术、放射治疗的计划制定、术后治疗的效果检验等介入手术方面。2D／3D图像配准的引入可降低上述医疗技术的实现难度，减少介入性治疗的创伤并提高手术精度。为了实现准确配准，科研工作者提出了大量的配准算法，基本可以分为基于特征［4－5］、基于灰度［4－7］和基于梯度［3］三类方法。其中，基于灰度的配准算法直接利用图像的灰度值进行配准，无需进行分割处理和人工介入，可实现全自动配准且精度较高，因而成为2D／3D医学图像刚性配准的主要研究方向。该算法基于数字重建影像（Digitally Reconstructed Radiographs，DRR）技术，首先采用Ray casting算法［4］将变换后的3D图像投影为2D图像即DRR图像，选取适当的相似性测度作为目标函数来衡量DRR图像与X-ray图像之间的相似程度，然后对目标函数进行优化，当函数达到最优时即代表获得最佳配准。

近年来，在基于灰度的配准算法中，科研人员对相似性测度和优化方法做了一定的对比研究［4－5，8］，以评定相似性测度和优化算法对配准精度和鲁棒性的影响。Penney等人［4］对归一化相关（Normalized Cross Correlation，NCC）、互信息（Mutual Information，MI）、差值图像的熵（Entropy of the Difference Image，EDI）、梯度相关（Gradient Correlation，GC）、梯度差分（Gradient Difference，GD）和模式强度（Pattern Intensity，PI）6种相似性测度进行了对比分析；Maes等人［5］研究了Powell方法、单纯形法（Simplex，SMP）、梯度下降法（Steepest Gradient Descent，STD）、共轭梯度法（Conjugate Gradient，CJG）、拟牛顿法（Quasi Newton，QSN）和列文伯格－马夸尔特法（Levenberg Marquardt，LVM）6种优化算法对基于互信息的2D／3D图像配准的影响，然而在2D／3D图像配准中，仅仅考虑相似性测度或者优化方法对配准结果的影响是不够的，因此，本文结合6种相似性测度和4种优化方法在公开发表的“金标准”数据［2］上进行2D／3D图像刚性配准实验，并利用Kraats等人［6］提出的方法从配准成功率、平均迭代次数和平均配准时间三个方面对配准结果进行评估，分析不同的相似性测度和优化方法对图像配准的影响，并给出通用性最好的组合，为2D／3D图像刚性配准在临床中的应用提供理论基础。

2 相似性测度

在2D／3D图像刚性配准中，相似性测度是用来度量两幅图像配准程度的一个重要指标，可以衡量经过空间变换后浮动图像（DRR）与参考图像（X-ray）在空间上的一致性程度。因此，相似性测度的选择是否合理，直接影响到图像配准的准确性和稳定性。本文选取比较常用的6种相似性测度进行对比研究，它们是归一化相关、互信息、归一化互信息、梯度相关、梯度差分以及模式强度［4，7－10］。为了便于统一标识，定义IX( i，j)和IDRR( i，j)分别为X-ray图像和DRR图像中像素(i，j)处的灰度值。

2.1 归一化互相关（NCC）

在2D／3D图像刚性配准中，归一化互相关测度是通过求两幅图像的相关系数来表征二者间的相关程度，用公式可表示为：

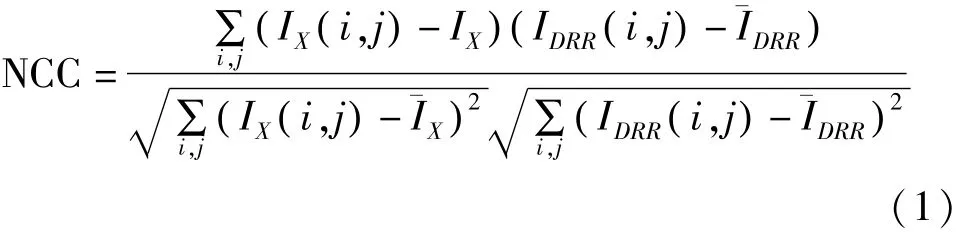
其中，IX，IDRR分别表示X－ray图像和DRR图像像素灰度的平均值。两幅图像越相似，该测度的值越接近1。

2.2 互信息（MI）

互信息是信息论里一种有用的信息度量，是指两个事件集合之间的相关性，一般用熵来表示。图像X的熵和图像X，Y的联合熵分别定义为：

其中，联合概率分布p( x，y)用归一化的联合直方图表示，p( x)、p( y)是p( x，y)的边缘分布概率。

因此，两幅图像之间的互信息可定义为：

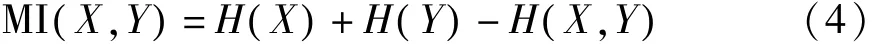
其中，()H X，()H Y分别是图像X，Y的熵；H X，()Y是它们的联合熵。在2D／3D图像刚性配准中，互信息的值越大，两幅图像的相似性程度越高；当互信息达到最大值时，表示两幅图像达到最佳配准。

2.3 归一化互信息（NMI）

由于互信息测度对配准图像间的重叠程度较为敏感，研究人员提出了归一化互信息的概念，其中Sthdholme等人［10］给出了其中一种形式，可表示为：

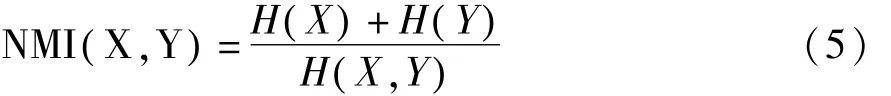
2.4 梯度相关（GC）

基于梯度的相似性测度首先要计算出两幅图像的梯度图像（本文采用Sobel算子），然后根据公式（1）分别计算出梯度图像在水平和竖直两个方向的归一化互相关，它们的和就是两幅图像的梯度相关，可表示为：

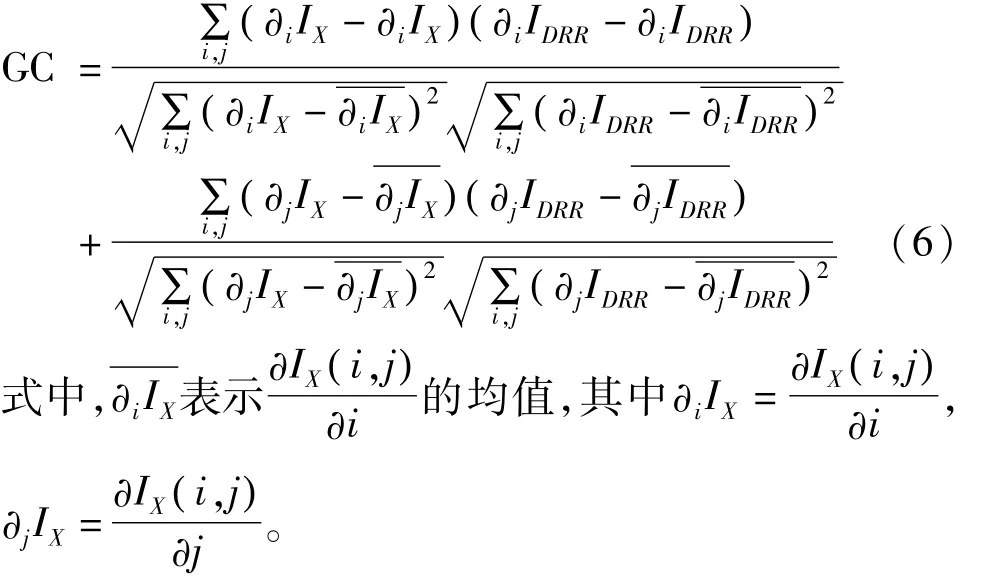
2.5 梯度差分（GD）

这种测度也是基于梯度图像，在得到各向梯度图像的基础上，比较两幅梯度图像间的差异，实际上是比较两幅图像的边缘方向信息。其计算公式如下：

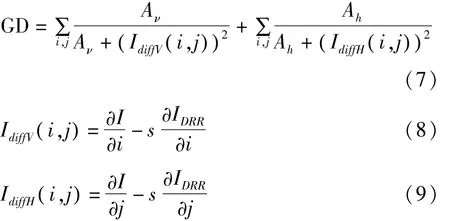
其中，Aν和Ah是X-ray图像分别在竖直和水平方向上的方差；s是衰减因子。IdiffV和IdiffH分别表示待配准图像在竖直方向和水平方向上的梯度差值图像。梯度差分测度通过使用1／（1＋x2）的形式增强了对细线结构的鲁棒性［9］，通过调整s，Aν和Ah的值可以使该测度更加平滑。

2.6 模式强度（PI）

该测度通过测量差值图像（两幅图像的灰度差）中所存在的模式是否降到最低来判断配准是否成功，其数学表达式为：

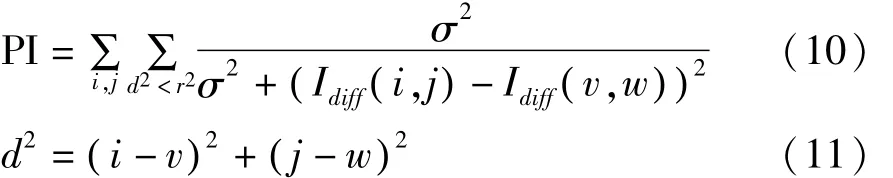
其中，σ，r是常量；Idiff( v，w)表示差值图像中(v，w)处的灰度值。模式强度认为，当一个像素与其临近的像素的值的差异显著时，该像素便属于一个模式，图像配准的过程就是要尽量消除这种差异［7，9］。图像达到最佳配准时，Idiff中待配准的模式会消失，其模式强度会最小，该测度的值最大。

3 优化方法

除了相似性测度以外，优化算法也会影响2D／ 3D图像配准的精度。医学图像刚性配准在本质上是一个多参数的最优化问题，即寻找相似性测度达到最大时所对应的6个空间变换参数的值，可由下式表示：

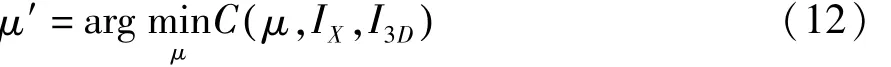
式中，C是由相似性测度构成的目标函数；IX和I3D分别是2D X-ray图像和3D体数据；μ是作用于体数据上的变换参数，μ′是图像配准时算法搜索到的最优参数。

最优化是一个迭代寻优的过程，可以采用如下迭代格式［11］表示：

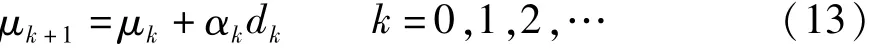
其中，dk表示第k次迭代时的搜索方向；αk是迭代步长。不同的优化算法对应着不同的搜索方向和搜索步长。文中选取4种优化方法用于搜索图像配准的最优空间变换参数，优化方法具体如下［5，8，11－13］。

3.1 梯度下降法（GRadient Descent，GRD）

梯度下降法又称最速下降法，其搜索方向沿着负梯度方向，目标函数可以最快的达到极小值，迭代格式可表示为：

3.2 非线性共轭梯度（Nonlinear Conjugate Gradient，NCG）

对于非线性共轭梯度，公式（13）中搜索方向dk可以表示为：

其中，βk公式有多种，Y H DAI，Y YUAN［12］给出βDYk的公式，Hestenes和Stiefel［8，12］给出βHSk的公式。本文采用的βk公式是二者的混合，即βk＝分别由下面两个公式求得：

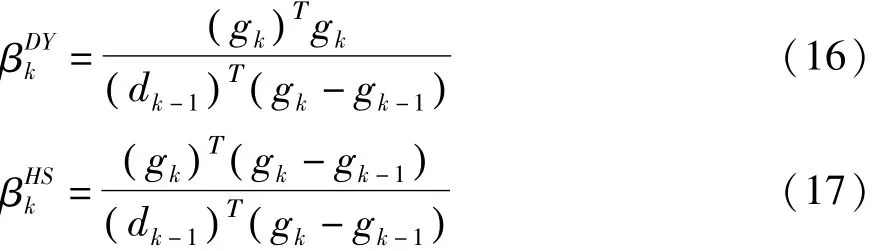
3.3 Powell算法

Powell算法［11］是直接搜索法中一种比较有效的方法，它不需要目标函数的导数信息，只要求目标函数连续即可。由于原始Powell算法中无法保证搜索方向是线性无关的，因此本文中采用的是改进后的Powell算法［11］。

3.4 拟牛顿法（Quasi Newton，QN）

拟牛顿法是牛顿法的直接推广，基本思想是构造海森矩阵的近似矩阵Bk或逆海森矩阵的近似矩阵Hk，通过在试探点附近的二次逼近引导拟牛顿方程来确定搜索方向。拟牛顿方程主要有两种形式：Hk＋1yk＝sk和Bk＋1sk＝yk，本文采用后者，其公式为：

其中，sk＝xk＋1－xk，yk＝gk＋1－gk，gk和gk＋1分别表示x在第k和第（k＋1）次的导数。

4 实验结果

本文实验采用MATLAB软件平台编程实现配准过程，同时结合CUDA技术，电脑配置为Intel Xeon E5645，2.4 GHz处理器，内存为48 GB，NVIDIA Tesla C2050显卡，显存为4 GB。

4.1 实验数据

在配准实验中，我们采用公开发表的2D／3D配准“金标准”数据［2］，该数据是对猪的颅骨进行成像得到的，包含3D的CT体数据和2D的X-ray图像。高斯滤波及各向同性采样到1mm后，CT数据的大小为326×326×330，X-ray图像尺度为410×410，如图1（a）所示。由于配准数据同时包含大量的软组织和硬组织，为提高配准精度，避免软组织对刚性配准的影响，同时缩短配准时间，实验选取包含软组织较少的圆形区域作为目标区域，其直径为200个像素。图1（b）是去除标记点的X-ray图像的兴趣区。

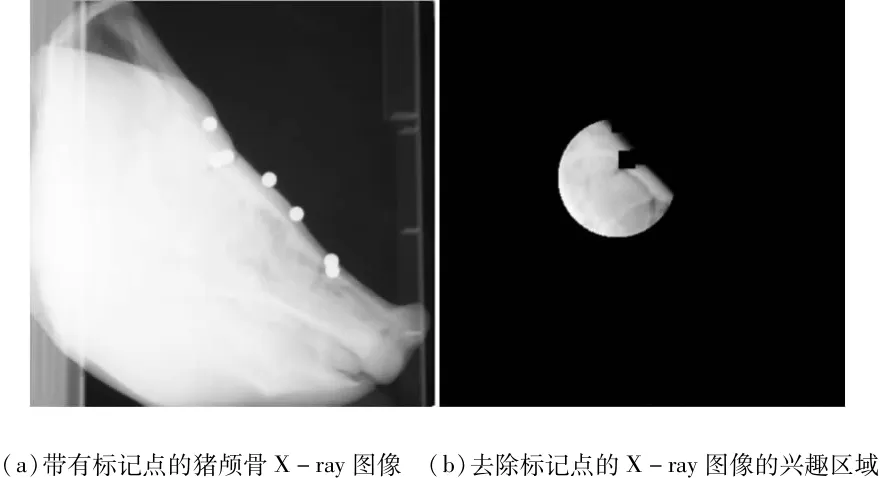
图1 猪颅骨X－ray图像

4.2 配准评估

根据Kraats等人提出的2D／3D配准评估准则［6］，本文从配准成功率（Success Rate，SR）、平均迭代次数以及平均配准时间三个方面对配准结果进行评估。配准成功率可以用平均目标配准误差（mean target registration error，mTRE）来计算，mTRE公式如下：

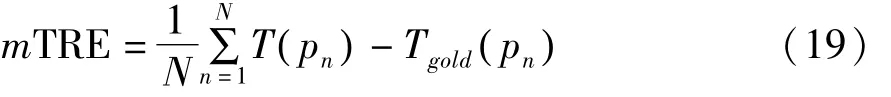
其中，T和Tgold分别表示配准后计算得到的变换矩阵T（由配准算法决定）和金标准变换矩阵Tgold，pn为在CT体数据中随机选取的目标点集。对“金标准”变换参数进行随机扰动后得到初始变换参数，使得初始mTRE分布在0～10 mm之间，并在每1 mm的间隔内再随机选取10个初始位置，这样就产生了总共100次初始变换。

4.3 参数设置

本文中所有参数均是参照以往的文献设置，对于梯度差分（GD），公式（7）中参数Aν和Ah均设为10，公式（8）和公式（9）中参数s均设为0.2。模式强度（PI）中参数σ设为10，r设为3，s设为0.2。

4.4 实验结果

文中对6种相似性测度和4种优化算法的不同组合进行配准对比，结果如表1和表2所示。由于“金标准”数据含有大量的软组织并且在使用Ray Casting时没进行优化处理来生成DRR图像，因此本文选取的配准成功阈值为8 mm，即最终目标配准误差（mTRE）小于8 mm视为配准成功。

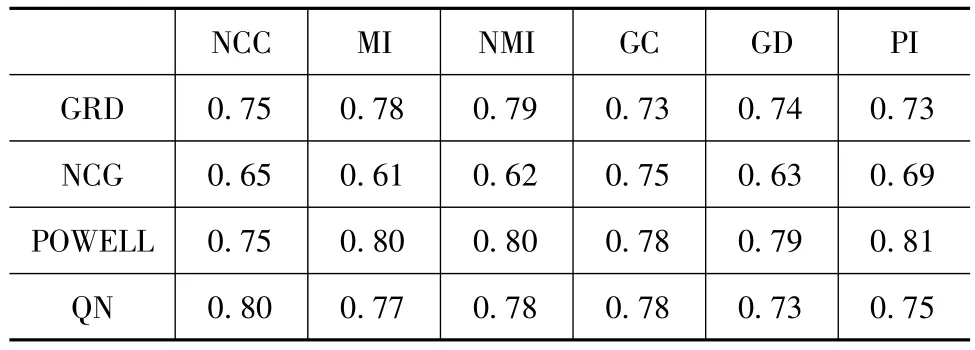
表1 所有相似性测度和优化算法所进行配准组合的成功配准率

由表1可以看出，配准成功率范围为0.61～0.81，最高成功率（0.81）的配准组合是PI和Powell组合，而最低成功率（0.61）的配准组合是MI和NCG组合。从结果中还可以看出，相同的相似性测度，Powell是成功率最高的优化方法，而NCG的成功率最低。

除了配准成功率，本文还从平均配准时间和平均迭代次数上对2D／3D刚性配准进行了评估，其中，平均配准时间是指一次完整配准所需的平均时间，平均迭代次数是指一次完整配准所需的平均迭代次数。

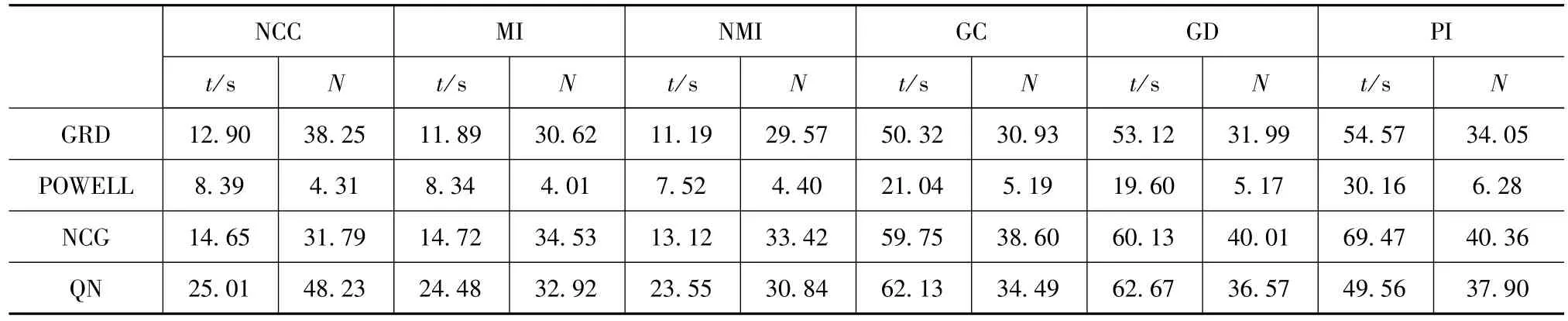
表2 所有配准组合的平均配准时间（t）和平均迭代次数（N）

从表2可以看出，后三种相似性测度（GC、GD以及PI）无论用什么优化策略进行配准所需时间都大于前面三种（NCC、MI以及NMI）。在所有的优化方法中，Powell所需的平均配准时间和平均迭代次数都是最少的。因此，在2D／3D图像刚性配准中，Powell成了最好的优化方法。

5 结 论

本文对6种相似性测度和4种优化方法的不同组合进行了2D／3D刚性配准对比研究，并从配准成功率、平均配准时间和平均迭代次数上进行了配准评估。结果表明，除了相似性测度会对2D／3D刚性配准产生影响外，优化方法的选择同样会影响配准效果。就本文而言，以PI（模式强度）作为相似性测度，用Powell进行优化搜索是最好的配准组合。此外，结果还表明Powell方法是2D／3D图像刚性配准最好的优化方法。

［1］ PMarkelj，D Tomaževiĉ，B Likar，etal.A review of3D-2D registration methods for image-guided interventions［J］. Medical Image Analysis，2012，16（3）：642－661.

［2］ PMarkelj，F Pernuš，SA Pawiro，et al.Validation for 2D／3D registration I：a new gold standard data set［J］.Medical physics，2011，38（3）：1481－1490.

［3］ Barbara Röper，Nassir Navab，Wolfgang Wein.2D／3D registration based on volume gradients［C］／／Medical Imaging International Society for Optics and Photonics，2005：144－150.

［4］ Jürgen Weese，Graeme P Penney，John A Little，et al.A comparison of similaritymeasures for use in 2D3D medical image registration［J］.IEEE Transactions on Medical Imaging，1998，17（4）：586－595.

［5］ FMaes，Dirk Vandermeulen，Paul Suetens.Comparative evaluation ofmultiresolution optimization strategies formultimodality image registration bymaximization ofmutual information［J］.Medical Image Analysis，1999，3（4）：373－386.

［6］ Graeme P Penney，Everine B van de Kraats，Dejan Tomaževiĉ.Standardized evaluationmethodology for 2D－3D registration［J］.IEEE Transactions on Medical Imaging，2005，24（9）：1177－1189.

［7］ Liang Wei.2D－3D registration ofmedical image［D］. Nanjing：Southeast University，2004.（in Chinese）梁玮.2D－3D医学图像配准研究［D］.南京：东南大学，2004.

［8］ IM Jvan der Bom，SKlein，M Staring.Evaluation of optimizationmethods for intensity-based 2D－3D registration in x-ray guided interventions［C］／／SPIEMedical Imaging International Society for Optics and Photonics，2001，7962（23）：1－15.

［9］ Wang Kai.The study ofmultimodality medical image regitration［D］.Changsha：Central South University，2008.（in Chinese）王凯.多模态医学图像配准研究［D］.长沙：中南大学，2008.

［10］D L G Hill，C Studholme，D JHawkes.An overlap invariant entropymeasure of 3D medical image alignment［J］. Pattern Recognition，1999.

［11］Sun Jingming，Ling Yingchun.Optimal design ofmachine［M］.Beijing：China Machine Press，2006.（in Chinese）孙靖明，梁迎春.机械优化设计［M］.北京：机械工业出版社，2006.

［12］Y H DAI，Y YUAN.An efficienthybrid conjugate gradient method for unconstrained optimization［J］.Annals of Operations Research，2001，103（1）：33－47.

［13］Ma Changfeng.Optimizationmethods and the design of its matlab program［M］.Beijing：Science Press，2010.（in Chinese）马昌凤.最优化方法及其Matlab程序设计［M］.北京：科学出版社，2010.

Comparison of sim ilarity measurement and optim ization methods in 2D／3D image registration

ZHANG Ran1，2，3，WANG Lei1，2，3，XIAWei1，2，3，GAO Xin2
（1.Changchun Institute of Optics，Fine Mechanics and Physics，Chinese Academy of Sciences，Changchun 130033，China；2.Medical Imaging Department，Suzhou Institute of Biomedical Engineering and Technology，Chinese Academy of Sciences，Suzhou 215163，China；3.University of the Chinese Academy of Sciences，Beijing 100049，China）

In surgical guide treatment，2D／3Dmedical image registration can provide the precise position of patient for surgeon.Accurate registration involvesmany aspects，such as similaritymeasurements and optimizationmethods.In order to investigate the influence of similarity measurements and optimization methods on 2D／3D image registration，a comparison of six similaritymeasurements in combination with four optimizationmethods is performed using the public and available porcine skull phantom datasets from Medical University Vienna.Comparison is performed for the registration results based on success rate，the number of iterations and execution time.The results show that themost accuracy registration is obtained by pattern intensity combined with Powell.Furthermore，the best 2D／3D registration results are obtained by Powell search strategy with fixed similaritymeasurement.

2D／3D image registration；rigid registration；similaritymeasures；optimization；registration evaluation

TP391

A

10.3969／j.issn.1001-5078.2014.01.022

1001-5078（2014）01-0098-05

国家自然科学基金项目（No.81000651）；苏州市科技计划项目（No.SH201210）；江苏省科技计划项目（No.BL2012049）资助。

张 冉（1988－），女，硕士研究生，研究方向为医学图像处理。

2013-05-20