基于Logistic映射和z－映射的图像分组加密算法

杨凤霞

（沧州师范学院计算机系，河北沧州061000）

基于Logistic映射和z－映射的图像分组加密算法

杨凤霞

（沧州师范学院计算机系，河北沧州061000）

针对图像加密，提出了一种基于Logistic映射和z－映射的图像分组加密算法，该算法在每一轮迭代中，交替使用矩阵置乱、非线性数值替换和数值关联混迭三级操作。经大量实验验证，该算法能够有效抵抗明文攻击、差分攻击、统计分析，密钥空间较大，因而安全性较高，并且加解密速度相当快，适用于数据存储。

Logistic映射；混沌序列；图像分组加密

1 引 言

由于图像表达信息直观、形象生动，所以图像的使用越来越广泛，它已经成为一种主流的信息表达方式。但是数字图像的安全保障问题也随之出现，并且已经成为一个备受关注的问题。许多学者就此开展了各种研究工作［1－3］，其中图像加密是保障图像安全的一个重要研究分支。目前，图像加密主要有基于混沌的图像加密，基于神经网络的图像加密以及基于细胞自动机的图像加密等。

近年来，一些学者运用混沌理论构造了密码算法，用于图像分组加密，这类算法的核心是交替地使用置乱和扩散机制，置乱是对图像的像素坐标进行变换，扩散是对图像像素值进行混迭［4－8］。林克正［6］等设计了一种Arnold映射和分段Logistic混沌映射相结合的双混沌系统，算法具有较高的抗攻击能力和初值敏感性。徐刚［7］等基于Logistic映射和Arnold映射设计了图像分组密码算法，通过交替迭代混沌系统实现了像素值的扰乱和位置置乱，迭代次数敏感地依赖于明文分组和密钥，具有可扩展性强和密钥空间大等特点。本文结合对前人分组加密算法的分析比较，提出一种基于一维Logistic混沌映射和z－映射的将置乱、替换和混迭三者结合的数字图像分组加密算法。实验验证，本算法具有较大的密钥空间，安全性较高，并且加解密速度也相当快，因而比较适用于数据存储。

2 算法原理

2.1 一维Logistic映射

一维Logistic映射模型简单，具有确定性，但有极为复杂的动力学行为，其方程定义如下：

其中，r为分支参数，当0≤r≤3.569945972……时，该动力系统因从稳定状态到分叉而产生倍周期，当3.569945972……＜r≤4时，该动力系统进入混沌状态。

2.2 z－映射

文献［9］中给出了一个与k阶Chebyshev映射非常类似的一维非线性动态系统，其定义式为：

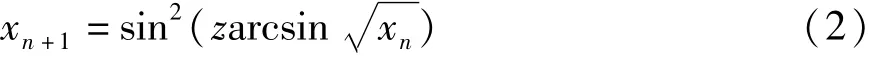
此处z为整型参数，由该式可以看出，此映射与一维Logistic映射具有完全一样的混沌吸引域和值域，但结构却完全不同，且其Lyapunov指数为λ＝ln z，当z＞1时，系统处于混沌状态。本文中将式（2）称为“z－映射”。

3 算法设计

算法设计思想：将整个图像分成或填充成若干256×256大小的数据块，通过多轮迭代完成对各数据块统计特性的改变。在每一轮迭代中，交替使用矩阵置乱、非线性数值替换和数值关联混迭三级操作。

3.1 置乱变换

置乱即对图像的像素坐标进行变换。

算法1 用z－映射序列等间隔调制Logistic混沌序列

Step 1将初值x0带入式（2），迭代生成序列｛yj，j＝1，2，……｝；

Step 2令x0′＝｜x0＋y1｜／2，将新的初值x0′带入式（1），迭代生成相应的混沌序列｛xi，i＝1，2，……｝；

Step 3每间隔n（n∈N）个数据，令x0′＝｜xj＋n＋yj｜／2（j＝1，2，……），不断代入式（1）迭代生成混沌序列Xn；

Step 4对Xn进行2m连续等分，并设定奇偶区间，用Xn落入区间的奇偶性来判定bn的0、1值，按式（3）生成所需长度的二进制序列：

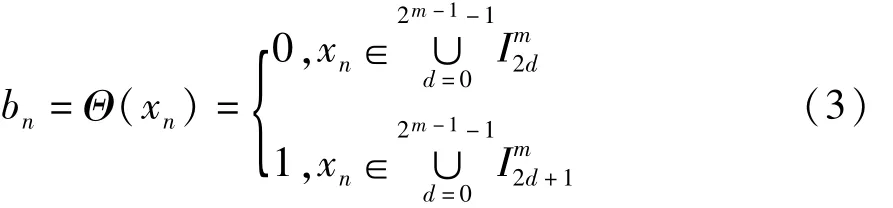
其中，m＞0，为任意的正整数（如m＝1000），Im0， Im1，…，Im2m－1代表Xn上的2m个连续的等分区间。

算法1采用双混沌映射，所得的混沌二进制序列具有非常好的伪随机性，所以克服了离散混沌系统中动力学退化、单个混沌迭代轨迹暴露等问题，提高了算法的安全性。

3.2 数值替换

算法2 排序方式生成替换表

选定Logistic映射进行迭代产生混沌序列，舍弃前200个数值，然后从后续数据中选出256个不重复的数值进行递增或递减排序，则该段数据的原始位置序号与排序后序号构成一个值域为1～256的整数替换表。具体替换算法为：

加密过程：

解密过程：

其中，I（i）为图像的第i个数据（已经一维化）；T为替换表数组；C（i）为经过替换表替换后的第i个图像数据。

算法2生成的替换表是一种非线性替换，为了达到更好的扩散目的，还需结合异或、取模等操作进行混迭。

3.3 混迭变换

算法3 耦合混迭变换

为了将前一点的影响耦合到下一点上，利用式（6）、（7）、（8）、（9）对相邻两点进行异或操作，如此循环，直到将一点的数值扩散到整个图像上。

加密过程：

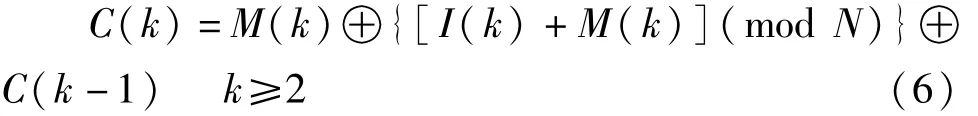
解密过程：

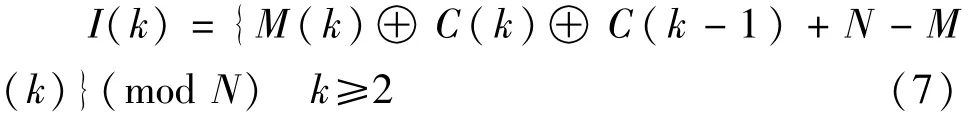
第1点加密：

第1点解密：

其中，I（k）为第k次混迭时的明文数据；C（k）为第k次混迭后的密文数据；M（k）为算法1所得的混沌二进制序列。

算法3将混沌映射得到的整数密钥序列与图像相邻像素按照式（6）到式（9）进行异或和取模运算，由于算法1得到的M（k）分布比较均匀，所以图像得到很好的混迭，从而使得选择明文攻击失效。

3.4 基于Logistic映射和z－映射的数字图像分组加密算法

具体步骤如下：

Step 1 图像预处理。对给定的图像进行分割或填充，使之成为256×256的图像或图像块。

Step 2 产生密钥。初始密钥是一个192比特的序列，分成4组，将这4组比特流分别映射为（0，1）间的浮点数k1，k2，k3，k4，其中k1为置换变换初始密钥，k2为替换操作初始密钥，k3为混迭运算初始密钥，为了使每轮加密的密钥得到更新，设k4为新一轮加密k1，k2，k3的微调增量，计算公式为：k′i＝ki＋（j－1）× k4，i＝1，2，3，…，j为加密轮数，若k′i≥1，k′i＝ki。

Step 3 置乱变换。将k1代入算法1对明文图像进行位置置乱。

Step 4 数值替换。将k2代入算法2生成排序替换表，依据此表对置乱后的图像像素值进行数值替换。

Step 5 混迭运算。以k3为初始密钥，按算法3中式（6）和（8）对置乱替换后的数据进行混迭加密。

重复步骤3、4、5，直至完成L轮加密，每轮加密前用微调增量k4更新密钥。随着加密轮数的增加，算法加密强度越来越大。

3.5 解密流程

解密流程与加密流程对称，先用式（7）和式（9）进行反混迭，再用式（5）进行反替换，最后进行逆矩阵置乱变换，重复L轮即得解密图像。

4 算法仿真及测试分析

4.1 仿真实验

在PIII－1G CPU，256M内存和MATLAB 7.0软件平台下对本算法进行仿真实验。选定192比特数据“564328857649247568000100”为初始密钥，将其映射为4个浮点数密钥k1＝0.564328，k2＝0.857649，k3＝0.247568，k4＝0.000100，对一幅256×256大小的灰度图像Lena进行仿真实验，其加解密效果如图1所示。由该图可知，本算法仅加密1轮即可取得良好的加密效果。

4.2 测试分析

4.2.1 密钥空间分析

本算法的密钥空间为2192≈6.2771×1057，同时生成混沌置乱矩阵和整数序列时多次用到Logistic映射、z－映射，控制参数和加密轮数均可算入密钥空间，因而本算法的密钥空间相当庞大，能有效阻止攻击者通过穷举法来解密图像。

图1 基于Logistic映射和z－映射的数字图像分组加密算法的加解密图

密钥敏感性测试：

测试一：对原图像用密钥“56432885764924756 8000100”进行5轮加密，然后任意改变1位密钥，如改变密钥k4的最低位，即用“564328857649247568000101”再对原图像进行5轮加密，比较两幅加密图像对应的不同像素的个数，图2给出了两幅加密图像及其差值，测试结果表明，两幅图像共有252个相同像素点，不同像素点所占比例达到了99.62%。

图2 密钥敏感性测试一

测试二：采用密钥“56432885764924756 8000100”对原图进行5轮加密，然后任意改变1位密钥，如改变密钥k3的最低位，即用“564328857649247568000100”进行解密，实验结果如图3所示。

测试表明，加密图像对密钥非常敏感，可以有效抵抗差分攻击。

4.2.2 统计攻击

加密图像的统计直方图：图4示出了对原始图像进行1轮加密过程中置乱、替换和混迭各个阶段所对应的直方图。

图4 1轮加密过程中各阶段对应的直方图

由图4看出，加密后图像的直方图与原始图像的直方图有很大的不同，且非常均匀。说明本算法仅加密1轮即可取得较好的效果，随着加密轮数的增加，安全性将逐渐加强。

相邻像素的相关性：一般原始图像中相邻两像素的相关性很大，为了阻止统计攻击，必须降低相邻两像素的相关性。随机选择5轮加密图像和原始图像中各2000对像素对，10次测算的平均值，观测其水平、垂直和对角方向的像素相关性，结果如表1所列。

从表1可以看出，加密前的图像像素之间具有较强的相关性，经过加密后，这种相关性基本被破坏了。

表1 原始图像和5轮加密图像相邻像素对之间的相关性

4.2.3 与DES算法的性能比较

本算法是一种典型的分组加密算法，包含了置乱、替代和混迭运算，加密强度与加密轮数有关。现代密码学中典型的分组加密算法（如DES、FEAL、LOKI、GOST、Lucifer、Blowfish、Khufu）的核心也是基于替换－置乱运算。以DES算法为例，将基于Logistic映射和z－映射的数字图像分组加密算法与经典加密算法在性能上进行简单的对比，结果如表2所列。

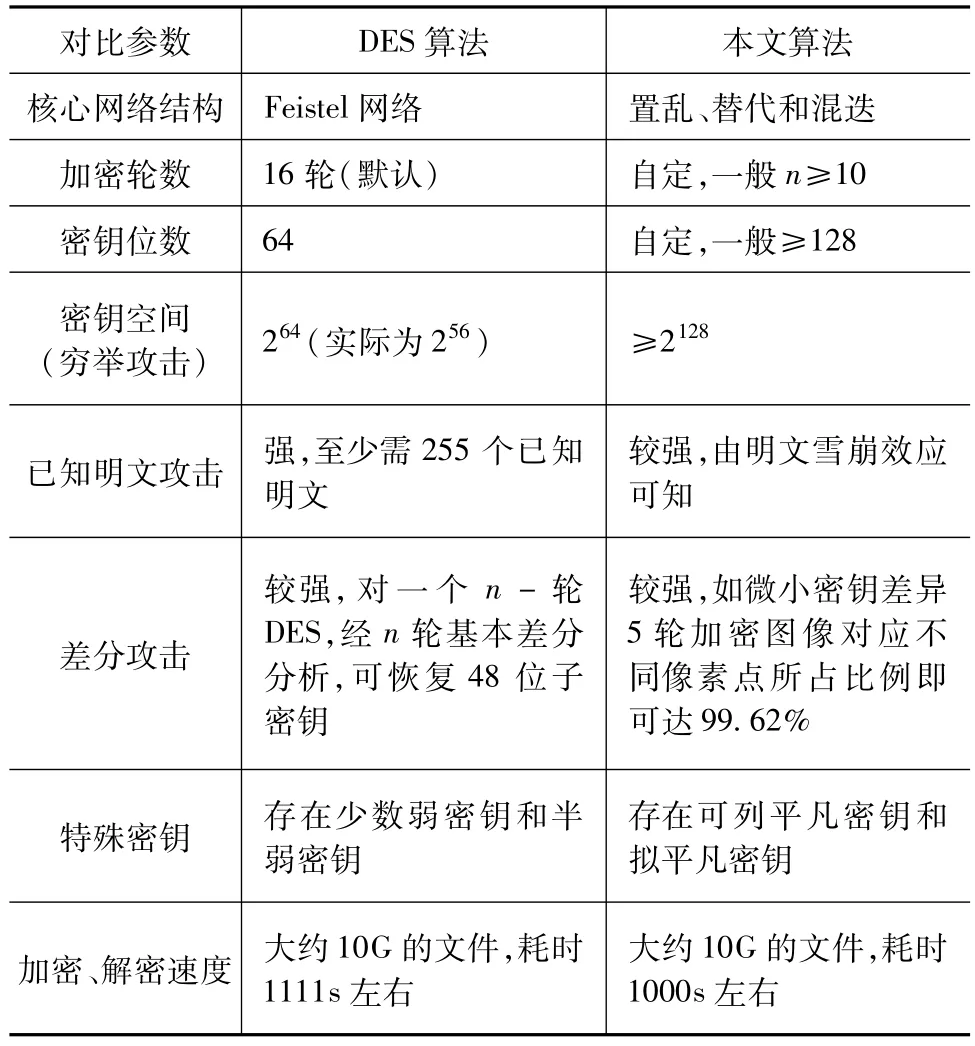
表2 本文算法与DES算法性能的简单对比

5 结束语

本文结合对前人分组加密算法的分析比较，提出一种基于一维Logistic混沌映射和z－映射的将置乱、替换和混迭三者结合的数字图像分组加密算法。本算法与其他分组加密算法相比，能够有效抵抗明文攻击、差分攻击、统计分析，密钥空间较大，因而安全性较高。数字化后的混沌系统只涉及整数运算，置乱变换与扩散变换的运行速度都比较快，因此该算法的加解密速度也相当快。但是本算法对诸如加噪、滤波、压缩等操作鲁棒性较差，因而较适用数据的存储。

参考文献：

［1］ Patidar V，Pareek N K，Sud K K.A new substitution-diffusionbased image cipher using chaotic standard and logistic maps［J］.Com mun Nonlinear Sci Numer Simul，2009，14（7）：3056－3061.

［2］ Hu Chunqiang，Deng Shaojiang，Qin Mingfu，et al..Image encryption algorithm based on logistic and standard map［J］.Computer Science，2010，37（12）：57－59.（in Chinese）胡春强，邓绍江，秦明甫，等.基于Logistic与标准映射的数字图像加密算法［J］.计算机科学，2010，37（12）：57－59.

［3］ Zhu Zhiyu，Zhang Daihua.Watermarking algorithm based on DWT and chaotic encryption［J］.Laser＆Infrared，2006，36（5）：417－420.（in Chinese）朱志宇，张代华.基于离散小波变换和混沌加密的图像水印算法［J］.激光与红外，2006，36（5）：417－420.

［4］ Chen Yanfeng，Li Yifang.Image encryption algorithm based on recipro-cally-disordered diploid chaotic sequences alternated in subsec-tion［J］.Journal of South China University of Technology：Natural Science Edition，2010，38（5）：27－33.（in Chinese）陈艳峰，李义方.交替分段相互置乱的双混沌序列图像加密算法［J］.华南理工大学学报：自然科学版，2010，38（5）：27－33.

［5］ Wang Qingsong，Fan Tiesheng.Chaotic image scrambling algorithm based on location and gray transformation［J］. Journal of Chinese Computer Systems，2012，33（6）：1284－1287.（in Chinese）王青松，范铁生.基于位置和灰度变换的混沌图像置乱算法［J］.小型微型计算机系统，2012，33（6）：1284－1287.

［6］ Lin Kezheng，Zhong Yuan.Image encryption technology based on dual chaotic maps［J］.Computer Engineering and Applications，2010，46（36）：195－197.（in Chinese）林克正，钟媛.双混沌映射的图像加密技术［J］.计算机工程与应用，2010，46（36）：195－197.

［7］ Xu Gang，Zhang Yadong，Zhang Xinxiang，et al.Digital image encryption algorithm based on an alternating iterative chaotic system［J］.Journal of University of Science and Technology Beijing，2012，34（4）：464－470.（in Chinese）徐刚，张亚东，张新祥，等.基于交替迭代混沌系统的图像加密算法［J］.北京科技大学学报，2012，34（4）：464－470.

［8］ Zhang Hualin.Research on applications of chaos-based encryptions［D］.Chongqing：Chongqing University，2006.（in Chinese）张林华.基于混沌的密码技术应用研究［D］.重庆：重庆大学，2006.

［9］ Mao Yaobin.Research on chaos based image encryption and watermarking technology［D］.Nanjing：Nanjing University of Science and Technology，2003.（in Chinese）茅耀斌.基于混沌的图像加密与数字水印技术研究［D］.南京：南京理工大学，2003.

Image grouping encryption algorithm based on Logistic mapping and z-mapping

YANG Feng-xia
（Computer Department of Cangzhou Normal University，Cangzhou 061000，China）

Aiming at the image encryption，a kind of image grouping encryption algorithm based on logistic mapping and z-mapping is put forward.In each iteration of this algorithm，the matrix scrambling，the nonlinear numerical replacement and the numeral value iteration are alternately used.By a large number of experimental verification，this algorithm can effectively resistplaintextattack，differentialattack and statisticalanalysis，and ithas larger key space and higher security，and the speed of encryption and decryption is quite fast，which is suitable for data storage.

Logistic mapping；chaotic sequence；image grouping encryption

TN918

A

10.3969／j.issn.1001-5078.2014.01.023

1001-5078（2014）01-0103-05

杨凤霞（1971－），女，硕士，讲师，研究方向为数据挖掘。E-mail：szyfx＠163.com

2013-05-22；

2013-06-26