基于季节ARIMA模型的地下水位动态预测

黎 广，黎 亮，韩慧平

（1.江西省水利规划设计院，江西 南昌 330029）

基于季节ARIMA模型的地下水位动态预测

黎 广1，黎 亮1，韩慧平1

（1.江西省水利规划设计院，江西 南昌 330029）

通过分析1996～2004年测井实测逐月地下水埋深序列的趋势性和周期性，建立了合适的季节ARIMA模型，并运用该模型对2005年逐月地下水埋深进行预测，预测值与实测值变化趋势一致，平均相对误差为2．5%，证明该模型用于地下水水位预报是可行的。

地下水位动态；季节ARIMA模型；预测

对地下水位动态进行微观预测与宏观分析是城市供水调度、地面沉降防治策略设计、工程施工降水方案设计等领域不可缺少的重要环节[1]。由于受自然因素（气候、水文、降雨等）及人为因素（排水、人工回灌等）影响，地下水动态的变化是非常复杂的非线性系统[2]。目前，可通过确定性数学模型和随机性数学模型研究和预测地下水位动态变化[3]。由于需要大量实测数据和水文地质参数，确定性方法的适用性较差，而随机性方法是通过挖掘原始数据资料本身所蕴含的信息建立系统模型来进行预测，则更加灵活。时间序列分析作为一种数据驱动分析技术，因其避免了序列变量诸多影响因素之间的复杂关系，使序列的分析和模拟过程大大简化，已被广泛用于地下水资源评价和预报[4-6]。

地下水动态变化常有昼夜的、季节的及多年的周期性变化特征。平稳时间序列模型，如自回归(AR)模型、滑动平均（MA）模型、自回归滑动平均模型(ARMA)等无法处理可能存在非平稳趋势的序列，ARIMA模型则未考虑时间序列中可能存在的周期性特征。季节时间序列（SARIMA）模型可综合考虑序列的趋势变化、周期变化和随机干扰，并借助模型参数进行量化表达，是描述具有周期变动特征的时间序列的有效建模方法。本文尝试运用SARIMA时间序列模型对逐月地下水埋深序列进行分析，揭示地下水动态变化规律，为地下水规划和管理提供依据。

1 季节ARIMA模型

设{xt, t=0,1,…}是一随机序列，L表示时间滞后的算子，即Lxt= xt-1。Δ表示差分运算的差分算子。如果存在非负整数d，Δd=(1-B)d，得：

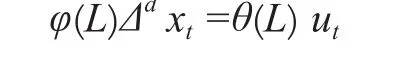
式中，φ(L) =1 -φ1L-φ2L2-…-φpLp；θ(L)=1-θ1L-θ2L2-…-θqLq；ut为白噪声序列；则称{xt}为求和自回归滑动平均序列[7]，记为ARIMA(p,d,q)，其中d为差分阶数，p为自回归阶数，q为滑动平均阶数。

在实际问题中，一些随时间递增而呈周期性变化的随机序列往往是不平稳的，只用平稳时间序列模型或求和自回归滑动平均模型进行处理是不够的[8]。描述这类序列的模型之一是SARIMA模型。该模型首先用季节差分消除周期性变化。季节差分算子定义为：Δs=1-Ls。序列xt一次季节差分表示为：

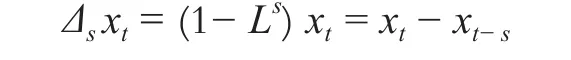
对于非平稳季节性时间序列，有时需进行D次季节差分之后才能转换为平稳序列。在此基础上可建立关于周期为s的P阶自回归Q阶移动平均季节时间序列模型：

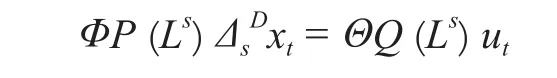
当ut非平稳且存在ARMA成分时，SARIMA (p, d, q) × (P, D, Q)s的一般表达式为：

式中，下标P、Q、p、q分别表示季节与非季节自回归、移动平均算子的最大滞后阶数；d、D分别表示非季节和季节性差分次数。当P = D = Q =0时，SARIMA模型退化为ARIMA模型；当P = D = Q = p = q = d =0时，SARIMA模型退化为白噪声模型。

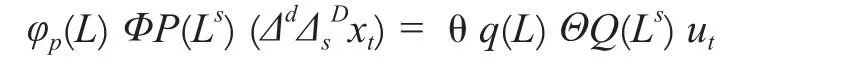
2 SARIMA预测模型建立与预测

对于SARIMA模型的建立，可通过差分处理将序列平稳化，即转化为ARMA模型来解决，其建模过程如下[9]：

1）根据序列的自相关性分析得出序列的季节性周期s。

2） 根据对序列的趋势分析分别得到d和D的估计，对序列进行差分处理，消除趋势性和周期性，得到新的平稳序列。

3）模型识别，根据序列的相关性确定相应的模型阶数的初始范围。

4）模型参数估计，用极大似然估计得到模型中所有参数的估计值，并根据信息准则来判定模型的拟合优度和模型残差的白噪声检验，确定最优模型。

5）运用最优模型进行预测。

6）精度评定。为评价模型的预测性能，本文采用相对误差Pe和平均绝对误差百分比MAPE对模型进行评价，表达式分别为：

3 应用实例

图1为南昌市某地下水观测井1996～2005年的实测月度地下水埋深序列，可以看出，多年来该地区地下水变化复杂，动态曲线表现出明显周期性变化的非平稳特征，周期为12个月。本文使用1996～2004年108个月度地下水动态的历史序列对2005年12个月水位动态进行预测，并将预测结果与相应的实测数据进行比较。

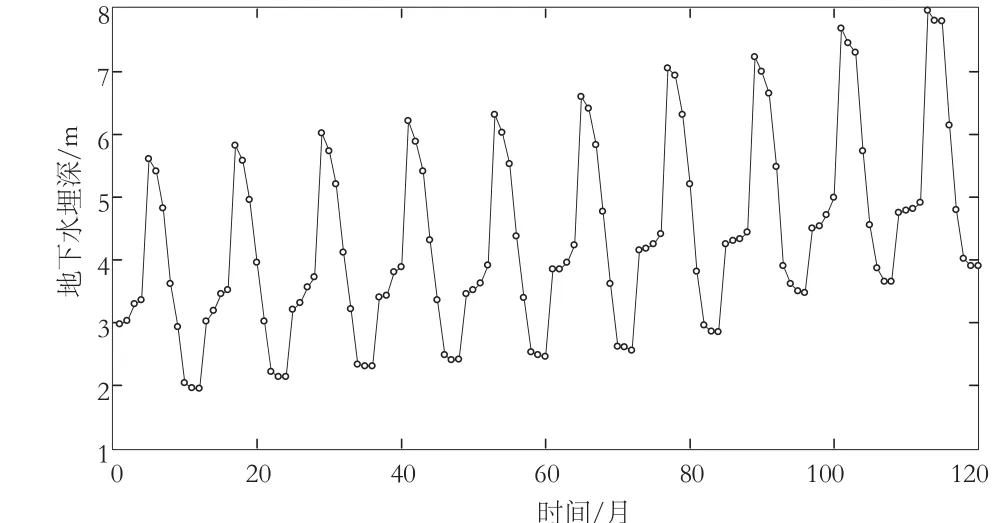
图1 地下水位动态序列图

由于原始序列具有周期变化特点和上升趋势，因此无法直接采用平稳时间序列方法对其建模，应首先对序列进行平稳化处理。由近似信号序列经一阶差分和季节差分后自相关系数图（如图2所示）可知，当P＞2之后时间序列的自相关系数都落入置信区间，则可认为经差分处理的序列是平稳的。

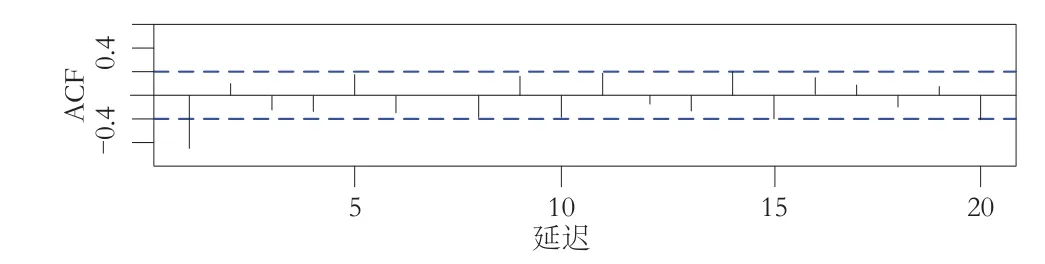
图2 一阶差分和季节差分后序列自相关系数

根据差分变换的次数，可初步确定模型是以12个月为周期的SARIMA(p,1,q)(P,1,Q)模型，其中p、q和P、Q是待定参数。由自相关系数可知，平稳化处理后的数据不含有季节相关项，故P = Q =0。选取不同的p,q(0≤p,q≤2)值，根据AIC准则对模型进行诊断，得出当p =1,q =1时，AIC值较小，且对模型拟合残差进行χ2检验。诊断结果表明，残差不存在相关性，可接受SARIMA(1,1,1)(0,1,0)模型最优。根据极大似然方法进行参数估计，估计结果分别为：φ1=0.436 1和θ1=-0.919 0，模型的数学表达式为：运用模型ARIMA(1,1,1)(0,1,0)12对2005年1～12月的地下水位埋深进行预测，预测结果如图3所示。除3、4月份的实测值落在预测值95%置信度区间之外，其余月份预测值均与实测值符合较好。表1为采用ARIMA(1,1,1)(0,1,0)12模型1～12月份的实测值与预测值的对比，由表可知，平均相对误差最大为8%，最小可达0．3%。再选用平均绝对误差百分比MAPE评价精度，求得MAPE=2．425%，可认为季节ARIMA模型对地下水埋深预报的结果是可靠的。

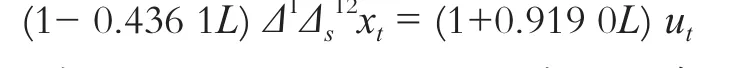
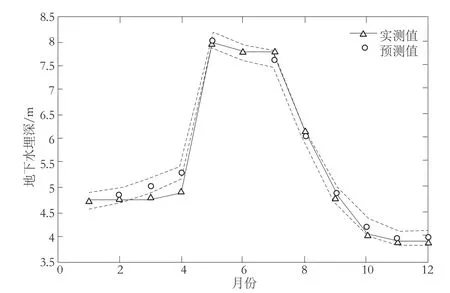
图3 2005年地下水位埋深的实际观测值与预测值比较图

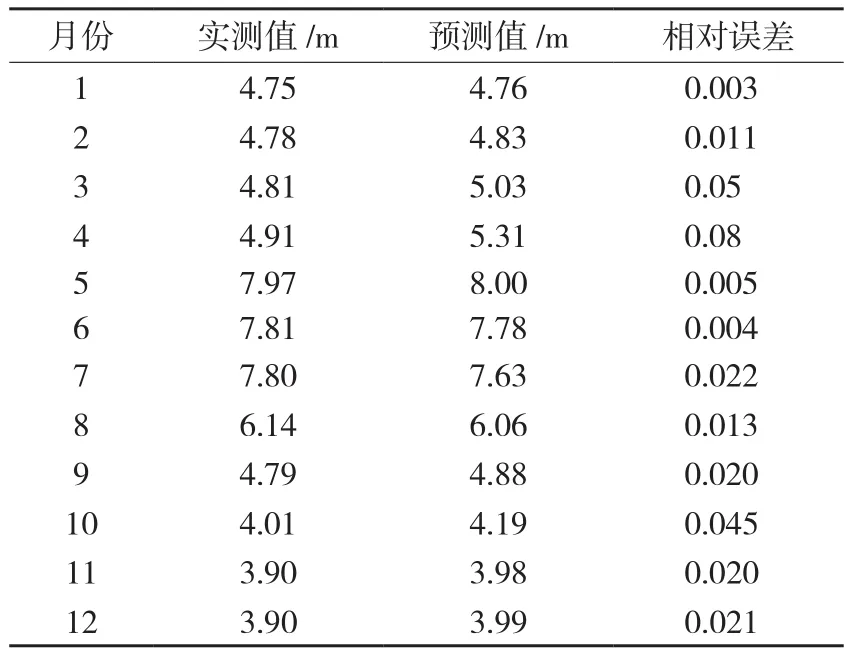
表1 2005年1～12月地下水埋深实测值与预测值表

4 结 语

地下水水位的变化可反映该地区地下水系统内部的变化规律，通过对地下水动态的预测，能有效实现对该地区水位的调控，对合理利用和管理地下水资源有重要意义。本文运用SARIMA模型对1996～2004年实测逐月地下水位动态序列进行了分析，建立ARIMA(1,1,1)(0,1,0)12模型，并应用该模型对2005年1～12月的地下水位埋深进行了预测，预测结果与实测变化符合较好，平均相对误差为2．5%，表明该模型可用于地下水位动态预测，为地下水资源评价和管理提供了依据。

[1] 吴东杰,王金生, 滕彦国． 小波分解与变换法预测地下水位动态[J]．水利学报,2004(5):1-8

[2] 杨建强,罗先香．地下水动态预测的径向基函数法[J]．工程勘察,2001(5):35-37

[3] 王新民,崔巍．变权组合预测模型在地下水水位预测中的应用[J]．吉林大学学报：地球科学版,2009,39(6):1 101-1 105

[4] 杨忠平,卢文喜,李平． 时间序列模型在吉林西部地下水动态变化预测中的应用[J]．水利学报,2005,36(12):1 475-1 479

[5] 栗现文,向东进,周金龙, 等． 时间序列分析方法在干旱区地下水位动态预测中的应用[J]．工程勘察,2011(12):28-32

[6] 卢文喜,杨磊磊,龚磊,等． 基于时间序列分析改进法的地下水位动态预报——以吉林省桦甸市为例[J] ．吉林大学学报：地球科学版,2012,42(增刊):367-372

[7] 杨建萍．基于ARIMA模型的用电量时间序列建模和预报[J]．工程数学学报,2008,25(4):612-615

[8] 刘付程,刘吉堂,苏伟,等．基于季节ARIMA模型的近海表层水温时间序列模拟与预测[J]．淮海工学院学报：自然科学版,2009,18(4):77-80

[9] 张辉,刘嘉焜,柳湘月,等．交通流的季节ARIMA模型与预报[J]．天津大学学报,2005,38(9):838-841

P208

B

1672-4623（2014）01-0149-02

10.11709/j.issn.1672-4623.2014.01.052

黎广，主要从事水利工程测量工作。

2013-04-17。

项目来源：国家自然科学青年基金资助项目(41204002)；民政部减灾和应急工程实验室开放基金资助项目（LDRERE20120102）。