基于主方向的SIFT误匹配点剔除方法

谭仁龙,万幼川

（1.武汉大学 遥感信息工程学院，湖北 武汉 430079）

基于主方向的SIFT误匹配点剔除方法

谭仁龙1,万幼川1

（1.武汉大学 遥感信息工程学院，湖北 武汉 430079）

针对RANSAC方法在剔除SIFT误匹配点方面的不足，提出了一种基于主方向的SIFT误匹配点剔除方法。结果表明，该算法与RANSAC相比，耗时较少，剔除效果更好，保留的正确匹配点数更多，且当误匹配点数量多于正确匹配点时也能得到很好的剔除效果。

影像匹配；SIFT算法；主方向；最小二乘；误匹配剔除

影像匹配即通过一定的匹配算法在2幅或多幅影像之间识别同名点的过程，是计算机视觉及数字摄影测量的核心问题[1]。大多数情况下，基于特征的SIFT[2]匹配算法能取得较好的结果，但当图像中存在大量相似结构时，匹配结果中会出现大量的误匹配。目前国内学者对于误匹配点的剔除提出了许多算法[3-6]，较常用的方法是用随机抽样一致性（RANSAC）随机选择样本点反复迭代计算来剔除误匹配点，但此方法在剔除误匹配点的同时也剔除了大量正确匹配点，且在初始匹配的内点少于50%时这种方法就会失效[2]。鉴于此，本文利用特征点间的主方向夹角近似相等作为初始约束条件，迭代使用最小二乘增加正确匹配点，最后实现误匹配点的剔除，以此提高SIFT匹配算法的可靠性和准确性。

1 SIFT影像匹配

SIFT算法主要包括尺度空间的极值探测、关键点的精确定位、确定关键点的主方向和生成关键点的描述子及匹配等内容。

在建立多尺度空间时，高斯卷积核已被证明是唯一的线性核[7]。为了有效提取稳定的关键点，Lowe提出了利用高斯差分函数对原始影像进行卷积，在高斯差分金字塔影像中将每个采样点与它所在的同一层比例尺空间的周围8个相邻点和相邻上、下比例尺空间中相应位置上的9×2个相邻点进行比较，如果该点是所有点中的极值，则作为一个候选点。通过拟合三维二次函数以精确确定关键点的位置，同时需要剔除低对比度的特征点和不稳定的边缘响应点，以保证特征点的稳健性。

在以关键点为中心的16像素×16像素邻域窗口内，利用高斯函数对各像素的梯度大小进行加权，用直方图统计窗口内的梯度方向，将直方图的主峰值方向设为关键点的主方向；然后以特征点为中心，在邻域内计算生成128维特征描述符；提取SIFT描述子之后，采用欧氏距离来计算描述子之间的相似度，对于参考图像中的某个关键点，找到其与待匹配图像中欧氏距离最近的前2个点，若最近距离除以次近距离小于某个设定的阈值，则认为这是一对正确匹配点。

2 基于主方向的误匹配点剔除

目前，影像误匹配点剔除算法主要是利用特征点的邻域灰度信息，而很少考虑特征点的主方向性质。如果任意2对特征点是正确匹配点，那么不仅对应正确匹配点对的邻域灰度信息类似，2个特征点的主方向的夹角也应是近似相等的。而错误匹配点对间虽然描述子的欧氏距离相隔很近，但是主方向的夹角一般偏差较大，因此，正确匹配点对间必须满足约束条件：

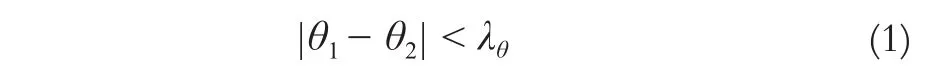
式中，θ1和θ2分别为参考影像和待匹配影像上两对应匹配点间主方向的夹角；λθ为单角度差阈值，这个性质对影像的平移、旋转、缩放甚至仿射变换都具有稳定性。影像之间的仿射变换满足公式：

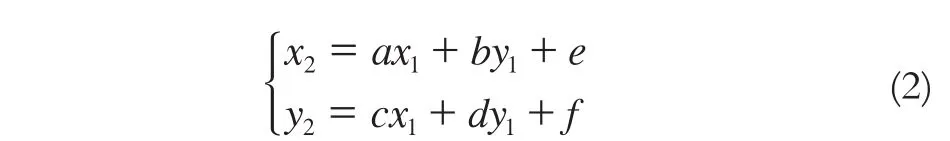
为求解6个位置参数，方程变形为：

求解此方程至少需要3对匹配点，因此遍历所有匹配点每次挑选3对匹配点，计算2幅影像对应匹配点两两主方向夹角差值的绝对值和f（θ）,当满足条件：式中，θ1、θ2、θ3为参考影像3个主方向夹角；θ1′、θ2′、θ3′为待匹配影像对应3个主方向夹角；σθ为三角差值和阈值。

为减少运算时间，对3个夹角差分别设置阈值，任意一个超过阈值则停止计算，寻找下一个匹配点。实际计算中由于阈值设定的差异，可能找不到不止3个最初匹配点，将这些初始点代入式（3）用最小二乘解算6个参数的初始值，再遍历所有匹配点，根据仿射变换方程计算出变换后每点坐标，与实际对应匹配点计算坐标差绝对值|Δ x|和|Δ y|，当两者同时小于设定阈值时认为其为正确匹配点，加入到正确匹配点集中，一次遍历完成后重新利用最小二乘计算6个参数，不断重复上述迭代计算过程，直到没有新的正确匹配点加入点集时停止计算。

3 实验结果与分析

为了验证方法的有效性，将本方法与RANSAC方法在不同数据下进行对比实验与分析。

实验1：实验数据包括近景影像和SPOT卫星影像，近景影像存在着旋转和缩放变化，卫星影像则存在平移变化。影像大小为：425像素×340像素、400像素× 300像素，实验中最近距离和次近距离的比例阈值设为0．4，单角差阈值设为0．05，三角差值和阈值设为0．003。实验结果如图1、图2所示。

从图1、图2可以看出，2种方法在剔除误匹配点的同时都剔除了一些正确匹配点，但本文方法保留的正确匹配点更多。图1a中SIFT匹配后船体右上角附近有一些正确点，但是经过RANSAC方法处理后均被剔除，本文方法处理后则大部分得到了保留，同时在船体其他部分的匹配点也比RANSAC方法留下的点要密集，图1d中RANSAC处理后左影像一匹配点在门内，而右影像上相对应的匹配点却在门外，明显是一对误匹配点却没有被剔除，而本文方法在相同位置附近则找到了2对正确匹配点，如图1e所示。对比图2a和b卫星影像可以发现，RANSAC处理后左片右侧部分损失了大量的正确匹配点，而左侧部分残留的点较原始SIFT匹配结果也稀疏了很多。经本文方法处理后，左侧残留点更加密集，右侧大多数点也得到了很好的保存，同时可在图2d中看到RANSAC处理后在道路上的匹配点位置存在明显偏差，本文方法则在相同位置附近找到了3对正确匹配点。2种方法处理的结果如表1所示，可以看到本文方法能剔除更多的误匹配点，同时能留下更多的正确匹配点，使得误匹配率大大降低，且对比实验1和实验2可知，处理速度相比RANSAC也有一定的优势。

图1 近景影像处理结果图

图2 卫星影像处理结果图

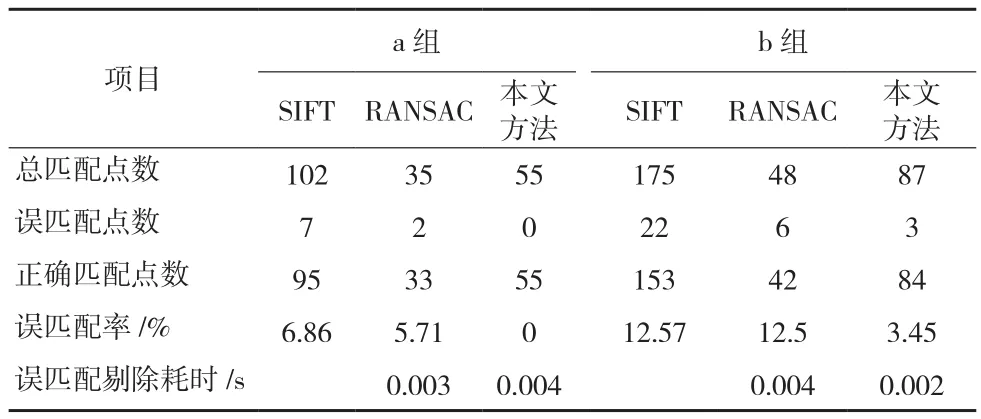
表1 2种方法剔除误匹配点结果比较表

实验2：所用的航空影像纹理比较均匀，且有较多的相似结构，影像间只存在上下平移的变化，影像大小为400像素×300像素，实验中最近距离和次近距离的比例阈值设为0．8。由于特征点周围影像纹理较均匀，一定程度上对主方向的生成精度造成了影响，考虑到可能存在的角度偏差，将角度差阈值设置较为宽松，单角差阈值设为0．1，三角差值和阈值设为0．15。用SIFT原始匹配结果及用RANSAC和本文方法分别处理的结果如图3所示，实验对比数据如表2所示。

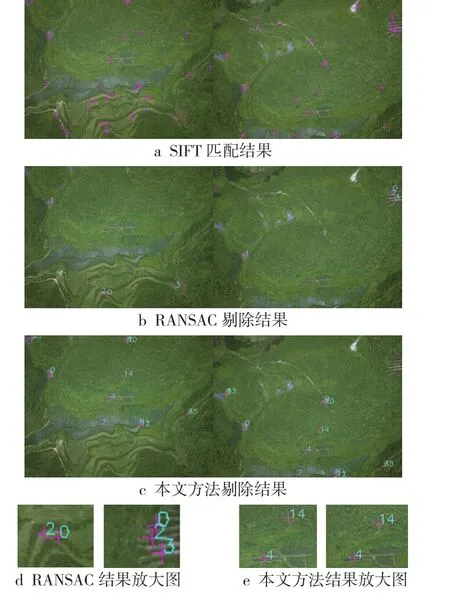
图3 航空影像处理结果

表2 实验2处理结果对比数据表

从SIFT匹配结果可知，影像中存在大量的误匹配点，数量超过了正确匹配点。由于RANSAC方法是按照不断随机选取样本点计算模型参数，用模型来确认内点，以得到内点数最多的模型作为正确模型，然后用内点重新修改模型的方法来剔除误匹配的，当正确匹配点数量少于误匹配点时，RANSAC随机选取的样本中正确匹配点的比例会变得很低甚至没有正确匹配点，这样计算出的模型参数往往不准确，难以用得到的模型区分正确点和错误点，因此该方法不再有效。由图3 b、图3 d可知，RANSAC处理后得到的4对匹配点只有1号点是正确点，其余3对点全是错误匹配点，而本文方法却可很好利用主方向夹角差几乎相等这一条件稳定地找到最初的几对正确匹配点，然后计算仿射模型参数，通过迭代使用最小二乘不断添加正确匹配点，最后实现误匹配点的剔除。从图3 c、图3 e中可知，本文方法找到了13对正确匹配中的12对，完全剔除了误匹配点，体现出了优势之处。

4 结 语

通过对基于主方向的误匹配点剔除方法和传统RANSAC方法在不同数据下进行实验，得出如下主要结论：

1）影像中正确匹配点多于误匹配点时，2种方法都能得到较好的剔除效果，相比于RANSAC方法，本文算法处理过后残留的误匹配点更少，保留的正确匹配点更多，耗时更少，因此效果更好。

2）影像中误匹配点多于正确匹配点时，RANSAC方法不再适用，而本文算法依然能够得到较好的剔除效果，弥补了RANSAC方法的不足。

3）本文算法中所涉及到的阈值参数均为人工设定，不同的影像需要不同的参数才能得到较好的剔除效果，如何能找到一种根据不同影像自适应计算最佳阈值的算法，是进一步的研究方向。

[1] 张剑清，潘励，王树根．摄影测量学[M]．武汉：武汉大学出版社，2002

[2] Lowe D G． Distinctive Image Features from Scale-Invariant Key Points[J]．International Journal of Computer Vision, 2004,60(2):91-110

[3] 张洁玉，白小晶，徐丽燕，等．基于空间描述符的SIFT误匹配校正方法[J]．中国图像图形学报,2009,14(7):1 369-1 377

[4] 陈敏，邵振峰，慎于蓝．基于基准点和基准方向的SIFT误匹配校正方法[J]．测绘通报，2012(3):16-18

[5] 张东兴，祝明波，邹建武，等．基于相似三角形的SIFT错误匹配点剔除算法研究[J]．计算机工程与科学，2012，34(4):66-70

[6] 李参海，王光辉．多源遥感影像误匹配点剔除的粗糙模糊C-均值方法[J]．测绘与空间地理信息，2008，31(5)：47-51

[7] Lindeberg T． Scale-Space Theory: A Basic Tool Analyzing Structures at Different Scales[J]．Journal of Applied Statistics,1994,21(2):224-270

P231.5

B

1672-4623（2014）01-0101-03

10.11709/j.issn.1672-4623.2014.01.035

谭仁龙，硕士，主要从事数字摄影测量与遥感方面的研究。

2013-05-27。

项目来源：国家科技支撑计划资助项目(2012BAH34B02、2012BAJ15B04、2011BAH12B03)。