基于GIS的东北三省气温降水空间自相关性分析

郑兴文，舒 红，许剑辉

（1．武汉大学 测绘遥感信息工程国家重点实验室，湖北 武汉 430079）

基于GIS的东北三省气温降水空间自相关性分析

郑兴文1，舒 红1，许剑辉1

（1．武汉大学 测绘遥感信息工程国家重点实验室，湖北 武汉 430079）

创新性地提出了基于两观测站点连线的垂直平分线构建空间连接矩阵，进一步计算空间自相关指数Moran′sI来分析气象数据的空间分布模式。利用Moran’sI分析探讨了东北地区86个气象站1951～2011年气温降水数据的空间自相关。结果表明，东北三省气温降水存在显著的空间聚集现象，降水表现为吉林省北部显著低低聚集，吉林辽宁省东部显著高高聚集，气温表现为东北三省南北区域显著聚集；1960～2011年气温分布较降水表现出更强的空间自相关性，且随年份变化自相关性稳定程度比降水好；气温分布空间自相关性随时间有减弱趋势,但仍表现出区域显著聚集强相关现象。

东北三省；气温；降水；Moran′sI；空间自相关

东北地区是我国重要的粮食生产基地，研究东北三省气候特性对东北农业生产具有重要意义。国内诸多学者深入分析了东北气候长期演变形态[1,2]和对农业、经济等方面的影响[3,4]，但较少研究东北三省气象的空间自相关性。研究气象空间分布相关性有利于分析气象地区间影响关系，便于获得哪些地区气候特性类似，从而对地区农业整体规划等提供指导。用Moran′sI指数来研究空间数据的相关性，分析数据区域聚集现象是地理信息分析中的一种重要功能。随着Moran函数的逐步完善[5-9]，特别是Moran散点图的诞生，代表Moran函数在空间自相关分析显著进步[10,11]。本文结合ArcGIS软件中Moran′s I功能分析了东北三省气温降水空间自相关性，试图从不同时间尺度的气温降水地区差异特性研究提供一种新的气象研究思路。通过分析气温降水空间效应，为东北三省气象研究提供参考。

1 研究区域概况及数据预处理

实验数据从中国气象科学数据共享服务网获取，经过处理加工获得东北三省区域降水观测站站点数据（共86个站点），站点地处东经119．7°～132．97°，北纬38．9°～52．97°之间，地区广阔，气候类型多样，冬季时间长，雨量主要集中在夏季。东北三省属于寒带大陆性季风气候，四季都是寒冰时期；地形以山地、平原、河流为主。站点数据包含1951年1月～2011年12月的日气温降水数据，通过计算获得各月份的平均气温降水值，其中少数测站的部分数据缺失，缺失月份平均气温降水值用相同月份总体均值代替。各测站点的分布如图1所示。

2 空间自相关分析

对于样本数据资料，大部分存在时间和空间上的自相关性，除了要计算其均值、方差外还要计算空间变异结构，这样才可以分析出空间（或时间）位置是否包含必要信息，才可揭示变量的空间（或时间）连续性[12]。空间自相关分析方法有全局Moran指数、全局G系数和Geary C系数，此外还有CliffOrd statistic、Join-count statistic 等国内统计界不常用的指标[13,14]。本实验主要运用Moran指数进行分析。

2.1 空间权重分析

空间权重用来表达不同位置空间区域的邻近关系，其确定规则一般分为4种：局域性关联、准局域性关联、准长程关联和长程关联。其表达形式如下：

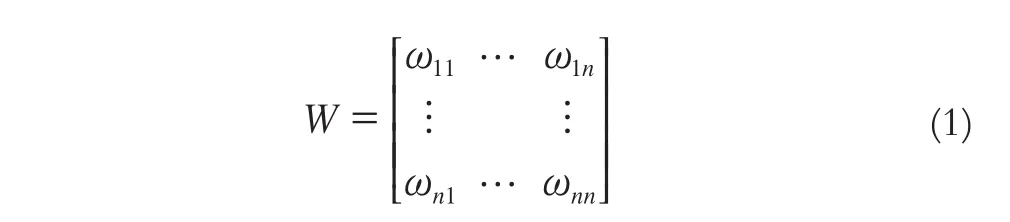
1）局域性关联：

其中区域相邻接也有广泛的定义，取决于所研究的问题。然而，大多数的空间自相关分析遵守一个共同的邻近关系定义。邻近关系表现为直接4邻域邻近、对角线方向4邻域邻近和8邻域邻近。区域邻近权重取1，否则取0。

2）准局域性关联：

式中，rij为i与j的距离；r为平均距离。

式中，b为距离摩擦系数（通常取b=1）。地理学家Cliff和Ord主要采用这个公式计算权重矩阵，故有时人们称之为Cliff-Ord权重。

本文根据泰森多边形代替站点数据方式选用第一种局域性关联直接4邻域邻接方式确定空间权重矩阵，进行空间相关性分析，即泰森多边形相邻时空间权重为1，不相邻时空间权重为0。

2.2 Moran模型

Moran指数I分为全局和局部2种[15]。全局空间自相关分析用来分析在整个研究范围内指定的属性是否具有自相关性，从而反映空间邻接或空间邻近的区域单元属性值的相似程度，即

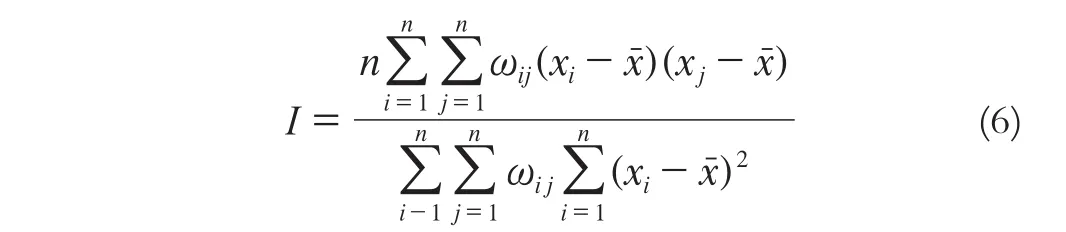
式中，Moran指数I取值在[-1,1]，当I＜0时，属性表示空间负相关，属性空间分布表现为离散特性；I=0时属性表示空间不相关，表现为随机特性；I＞0表示正相关，表现为聚集特性。

空间自相关的局部指标用来分析计算每一个空间单元与邻近单元就某一属性的相关程度。局部Moran指数被定义为：

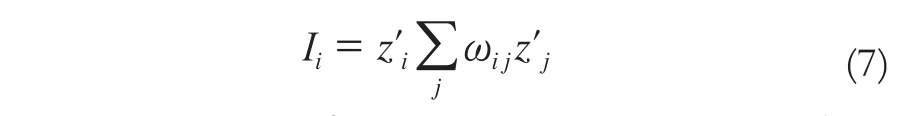
式中，Ii是Moran的局部指数；zi′和zj′是经过标准差标准化的值。当Ii显著大于0时，表明该i单元与其周围单元的属性值相似（高高聚集或低低聚集）；当Ii显著小于0时，表明该i单元与周围单元属性值不相似（高低聚集或低高聚集），即测值高（低）的区域被周围测值低（高）的区域包围。当Ii接近0时，表明该单元属性值与周围单元属性值无相关性。相关性的显著水平可通过z值和伪p值[7]（显著性水平）确定，z值越大，p值越小，相关性越显著。

3 结果与讨论

3.1 泰森多边形法分析区域聚类

泰森多边形最早用来解决气象站的降水量数据代替某地平均降水量的问题，因此首先利用ArcGIS构建泰森多边形[16]。采用相连气象台站点连接成Delaunay三角形，三角形各边垂直平分线围成一个多边形，用多边形中气象观测站的气温、降水值来代表这个多边形区域内其他未观测点的气温、降水值。构造泰森多边形可将点数据拓展成面数据，有利于空间自相关分析和表达。

3.2 Moran'sI对东北三省气温降水总体分析

通过对东北三省86个气象站1951～2011年气温、降水的月平均值进行全局Moran′sI分析，结果见表1。

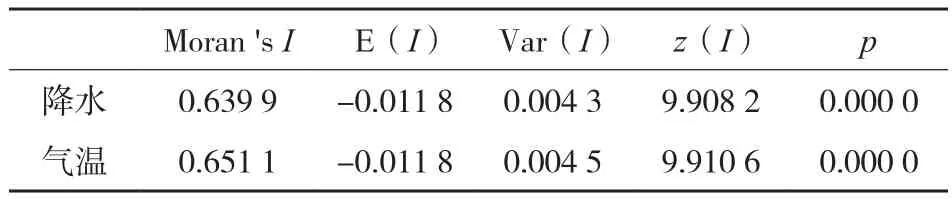
表1 东北三省气温降水全局Moran'sI指数

计算获得的东北三省气温、降水全局Moran′sI指数都大于0．6，且z值接近10，p值为0．000 0低于0．001的显著性水平。说明东北三省气温、降水存在显著的空间正相关性，即东北三省气温、降水具有显著聚集现象。用局部Moran′sI（见图2）分析具体聚集区域。

图2 a中红色区域表现为高高聚集模式，即降水多的区域被周围降水多的区域包围；蓝色区域表现为低低聚集模式，即降水少的区域被周围降水少的区域包围；高低聚集和低高聚集模式在图中不存在，即不存在降水多（少）区域被降水少（多）的区域包围的现象。图2 b温度的聚集模式解释类似降水。这说明，气温、降水表现为区域变化渐进过程。同时从图中可知，东北三省降水高高聚集区域为辽宁省东部和吉林省东南部，低低聚集区域为吉林省西部和黑龙江省西南区域，这是因为东北三省东部距黄海、日本海较近，气候湿润多雨，西部远离海洋而接近干燥的蒙古高原，气候干燥。气温的空间聚集现象表现为明显的南北差异性，黑龙江北部气温表现为显著低低聚集，而辽宁南部表现为显著高高聚集特性，说明气温聚集现象受纬度变化的影响。

图2 东北三省降水气温局部Moran'sI分析图

3.3 气温降水空间聚集现象随时间变化分析

通过研究1960～2011年东北三省的年平均气温降水Moran′sI（见图3），分析了气温、降水空间相关性在这52 a的变化特征。

图3 东北三省气温降水1960～2011年全局Moan'sI变化图

由图3可知，东北三省气温空间聚集程度随时间有下降趋势，但Moran′sI值仍显著大于0，表现出气温空间强聚集特性。而降水空间聚集程度随年份变化波动较大，但各年份均呈现出空间聚集现象。气温的空间聚集特性较降水空间聚集特性随时间变化波动小且空间聚集性明显比降水强，这说明东北三省气温空间聚集现象稳定而降水空间聚集性强度随年份变化表现出明显波动性。

4 结 语

自20世纪中叶至今，东北三省气温降水存在显著的空间聚集现象，气温以南北差异为主旋律，降水表现为吉林北部和辽宁东部、吉林东南部差异为主旋律。东北三省气温降水随年份不同，空间聚集特性表现不同。本文基于泰森多边形分区，区域数值用气象站点观测数据代替，多边形内部均质无变化，只是在边界上突变。而实际上气温和降水往往随距离的变化而表现为空间异质，要想获得更加具体的空间相关性分析，需要进一步对分区进行研究。同时气温降水不仅存在空间上的相关性，而且存在时间上的相关性，建立时空模型进行相关性分析是一个很有价值的方向。

[1] 娄德君,周秀骥．近50年来黑龙江省的冷暖和旱涝变化[D]．南京：南京气象学院,2003

[2] 于跃飞,谭秀青．东北地区平均温度和降水的时空演变[J]．科技通报，2006，22 (6):743-746

[3] 符琳． 东北三省农业气候年景评估研究[D]．北京：中国气象科学研究院，2011

[4] 刘志娟，杨晓光，王文峰，等．气候变化背景下我国东北三省农业气候资源变化特征[J]．应用生态学报，2009，20(9)： 2 199-2 206

[5] Moran P A P． The Interpretation of Statistical Maps[J]． Journal of the Royal Statistical Society B,1948, 37: 243-251

[6] Moran P A P． Notes on Continuous Stochastic Phenomena[J]．Biometrika,1950,37: 17-33

[7] Anselin L． Local Indicators of Spatial Association-LISA[J]．Geographical Analysis, 1995, 27(2) : 93-115

[8] Anselin L． The Moran Scatterplot as an ESDA Tool to Assess Local Instability in Spatial Association[C]． Spatial Analytical Perspectives on GIS, London: Taylor & Francis, 1996

[9] Getis A, Ord J K． An Analysis of Spatial Association by Use of Distance Statistic Geographical Analysis[J]．Geographical Analysis,1992, 24(3) : 189-206

[10] 陈小勇，林鹏．我国红树植物分布的空间自相关分析[J]．华东师范大学学报，2000，9(3) : 104-109

[11] Li Fei，Zhou Chenghu．Spatial Autocorrelation Analysis on Regional Economic Disparity of Northeast Economic Region in China[J]．Chinese Journal of Population，Resources and Environment，2009，7(2) : 27-31

[12] 张仁铎．空间变异理论及应用[M]．北京：科学出版社，2005

[13] Goodchild M F． Concepts and Techniques in Modern Geography[M]．UK: Geo Books, 1986

[14] Sawada M． Global Spatial Autocorrelation Indices-Moran′s I, Geary′s C and the General Cross-Product Statistic[EB/OL]．http://www．lpc．uottawa．ca/publications/moransi/moran．htm．2007-06-16

[15] 刘湘南,黄方,王平． GIS空间分析原理与方法[M]． 北京：科学出版社，2008

[16] 吴立新,史文中． 地理信息系统原理与算法[M]． 北京：科学出版社，2003

P208

B

1672-4623（2014）01-0049-03

10.11709/j.issn.1672-4623.2014.01.018

郑兴文，硕士，研究方向为时空统计分析。

2013-05-08。

项目来源：国家自然科学基金资助项目(41171313)；国家863计划重点资助项目(2011AA010502)；地理空间信息工程国家测绘地理信息局重点实验室开放研究基金资助项目(201329)；民政部减灾和应急工程重点实验室开放基金资助项目( LDRERE20120203)。