拓扑环小生境粒子群算法在无功优化中的应用
姜平,王昕,李立学,周荔丹,姚钢,陈洪涛
(1.上海交通大学电工与电子技术中心,上海 200240;2.上海交通大学电气系,上海 200240 3.吉林省电力有限公司松原供电公司,松原 138000)
电压质量对保证电力系统的安全稳定起着重要的作用,电力系统的无功规划[1]和无功平衡是保证电压质量的基本条件。合理地规划无功电源,控制无功的合理流动能有效地降低系统的有功损耗,从而获得不错的经济效益[2]。
无功规划是电力系统安全运行的一个重要组成部分,通过对电力系统的无功电源进行合理的配置,维持电网电压水平,改善电网稳定性,减少有功网络损耗[3]及保证有较宽的运行裕度。对于无功配置进行优化,传统的方法有线性优化方法中的内点法[4]和非线性优化方法中的混合整数规划法等。近年来又相继提出了遗传算法、Tabu搜索法、启发式算法、模拟退火算法、粒子群优化等智能优化算法[5]。与传统的优化方法相比较,遗传算法以生物进化为原型,具有收敛性好[6]、计算时间少、鲁棒性高等优点[7],但其计算量较大。文献[8]提出的粒子群算法PSO(paticle swarm optimization)从随机解出发,通过简单的迭代寻找最优解,通过对粒子适应度的计算来评判粒子的优劣。与遗传算法相比,实现上更加简单,收敛速度也有了明显的提升。但常规粒子群算法的重大缺陷可能会陷入局部最优[9];文献[10]提出了基于自适应小生境粒子群算法,根据各粒子之间的距离,利用共享机制改变粒子的适应度,提高了整个群体的全局优化能力。但其计算复杂度较基本粒子群算法有明显的增加,且必须具有一定的先验知识才能确定小生境参数[11],因而难以在实际中得到广泛应用。
本文提出了基于拓扑环的小生境粒子群算法TRNLPSO(topology ring niche particle swarm optimization)来进行配电网的无功优化。该算法在局部粒子群算法的基础上添加拓扑环,可以有效地控制粒子的收敛速度,更利于获得全局最优解。该算法首先对所有粒子进行编号,构成一个拓扑环;然后在该拓扑环上,选取相邻几个粒子构成局部粒子群,通过控制信息使其仅在局部粒子群中进行传播,不但可以实现对粒子收敛速度的有效控制,而且可以在局部进行更详尽地搜索,从而更利于获得全局最优解。相对于其他小生境粒子群算法,该算法仅在基本粒子群算法上引入拓扑环,其计算复杂度与基本粒子群算法相当,但该算法无需任何小生境参数即可自动形成小生境。最后以某配电网的有功网损作为优化目标,进行补偿容量的确定,仿真结果证明了该方法的有效性。
1 无功规划数学模型
电力系统中无功规划的作用是降低全网的无功损耗,同时使得节点电压保持稳定,从而达到减少费用和提高电网安全稳定运行系数的效果。
1.1 目标函数
本文选取系统有功网损(简称网损)和无功设备投资的综合费用作为目标函数,通过调整变压器电压变比、调节发电机端电压和投切补偿电容器等控制变量达到减少费用的目的。其全网综合费用的数学模型为

式中:Ploss为全网的有功网损;B为修正后的有功电价;Tmax为全网年最大负荷利用小时数;SB为基准功率;Y为补偿设备使用年限;r为无功补偿设备的数目;Ci为第i个补偿点的补偿设备经过修正后的单位容量的价格;Qc,i为第i个补偿点的补偿设备的容量,为控制变量。
考虑到实际计算中可能出现节点电压越限及发电机无功出力越限的情况,现将这些状态变量以罚函数即节点电压越限的惩罚项费用和发电机无功出力越限的惩罚项费用的形式来表达。添加到综合费用的数学模型中,得

式中:λV,j为节点电压越限惩罚因子;λG,i为发电机无功出力越限惩罚因子;coV为越界负荷节点电压下标的集合;coG为越界负荷发电机无功出力下标的集合;Vj,max、Vj,min分别为节点j的电压上限和下限;QG,imax、QG,imin分别为发电机i无功出力的上限和下限。其中

由式(3)可见,惩罚项只有在状态变量越限的时候才起作用。这样可以有效防止不合理的情况发生,因此,比仅以综合费用作为目标函数更合适。
1.2 等式约束方程
等式约束为
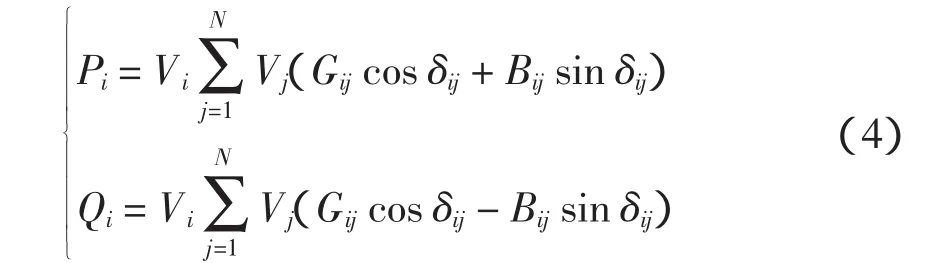
式中:Pi、Qi分别为节点i注入的有功、无功功率;Vi、Vj分别为节点i、j的电压幅值;Bij为节点i、j之间的电纳;N为与节点i直接相连的节点集合;Gij、δij分别为节点i、j之间的电导和电压相角差。
1.3 不等式约束方程
不等式约束方程为

式中:VG,imax、VG,imin为发电机机端电压的上下限;Tk,max、Tk,min为可调变压器变比的上下限;QC,imax、QC,imin为节点i上补偿容量的上下限;Vi,max、Vi,min为节点i电压幅值的上下限。
2 基于拓扑环的小生境粒子群算法
2.1 粒子群算法
粒子群优化算法[12]PSO是近年来发展起来的最主要的群智能算法之一,起源于生物学家对鸟群捕食行为的研究。Kennedy和Eberhart于1995年提出了粒子群算法,该算法是模拟鸟群群体觅食和迁徙行为的一种群体智能演化算法,较之其他智能算法具有一些很好的特点,如采用分散式搜索,具有并行处理及鲁棒性好的特点;具有记忆性,所需元件较少易于实现,并能以较大概率找到最优解。
针对具体问题,每个寻优问题的解都被想象成一只鸟,也即粒子群算法中的一个粒子。每个粒子包含一个速度矢量,以决定其飞行的方向和距离。所有的粒子都有与其对应的适应值,该适应值用来评判每个粒子的优劣。同时每个粒子都具有记忆性,能够记住历史中找到的最佳位置,即所求问题最优解。
为加快PSO的收敛速度,通常会在速度迭代公式中加入惯性因子对其进行修正,修正后的粒子速度和位移公式分别为

式中:ω为惯性因子;Xid为粒子位置;Vid为粒子速度;C1、C2均为加速系数;rand()为[0,1]之间的随机数;pBestid为个体最优,是当前找到每个粒子自身的最优值;gBestid为群体最优,是当前找到所有粒子的最优解。
通过式(6)、式(7)可以看出,粒子参考其个体最优及所有粒子的群体最优,对其速度和位置进行更新,使得粒子向个体最优及群体最优靠拢,以达到最优解。
2.2 基于拓扑环的小生境粒子群算法
在PSO中,粒子间相互作用起着关键的作用。在基本PSO中,所有粒子通过gBestid来进行信息的直接交流,实现最优信息的传播。这种方式虽然使信息得到了共享,但信息传播速度过快,当传播速度大于所需传播速度时,会导致陷入局部最优。
本文提出的基于拓扑环[13]的小生境算法是在局部PSO基础上加上拓扑环。以一个8粒子种群为例,通过对每个粒子进行编号,可使得8粒子种群在逻辑上形成一个拓扑环,如图1所示。在拓扑环中,每个粒子只与邻近的2个粒子有直接的交流,而与其他粒子只存在间接交流的关系。这样构成的拓扑环可以起到降低信息传播速度的作用,从而避免了由于信息传播速度过快而导致陷入局部最优。

图1 8粒子种群Fig.1 Population of eight particles
粒子群算法中,每个粒子都会记录自己所经历的最优解,因此可将粒子群看成2个群体的总和。第1个群体为开拓群,由粒子群的各个粒子组成,在求解空间中不断地更新迭代,变换十分频繁;第2个群体为记忆群,由每个粒子的历史最优解组成,相对于开拓群而言记忆群是相当稳定的,只有当当前粒子找到更优解的时候才会发生变化。
针对带有拓扑环的8粒子种群,开拓群由标注为1~8的粒子组成,记忆群由标注为m1~m8的粒子组成,如图2所示。每个粒子有3个消息提供者,其中2个来自临近粒子的记忆,1个来自自己的历史最优解。同样的,每个粒子的记忆也有3个消息提供者,2个来自临近粒子,1个来自粒子本身。
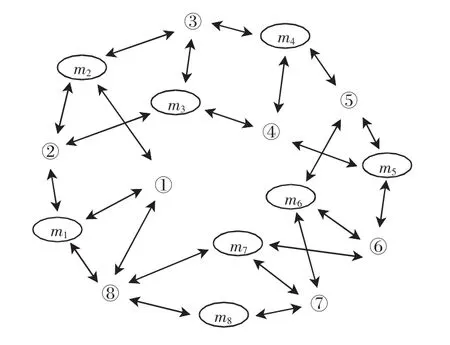
图2 开拓群和记忆群相互作用Fig.2 Interaction between exploit population and memory population
由图2可以看出,在向整个群体传播信息之前,每个粒子都会在其局部领域进行更细致地搜索。小生境粒子群算法的具体实现公式为

式中:pBestn,i为领域内粒子的历史最优解,即pBestn,i-1、pBestn,i和pBestn,i+1三者中的最优解。
拓扑环相邻粒子的相互作用如图3所示。拓扑环中的不同粒子可以拥有不同的pBestn,在这样的情况下,粒子群在计算完毕后分散在不同峰值上。由此可见,拓扑环不仅提供了一种机制来减缓粒子群中信息传播的速度,同时也允许不同邻域最优的共存。随着迭代的进行,粒子群中的粒子会向不同的区域聚集,自发地形成各个小生境。

图3 拓扑环相邻粒子的相互作用Fig.3 Interaction among adjacent particles in topology ring
图4所示为一个多峰值的函数曲线。1个粒子的历史最优解和邻域最优有可能在1个波峰下,也有可能在不同的波峰下。
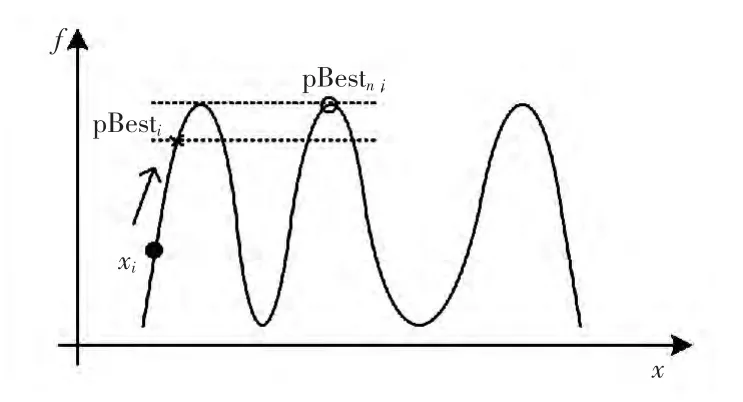
图4 某多峰值函数的函数曲线Fig.4 Function curve of a multi-peak function
(1)当历史最优解和领域最优在同一个波峰下时,粒子本身及粒子的历史最优解很大可能向粒子的邻域最优解靠拢,最终结果为

而粒子的速度vi将会减小,直至为0,粒子最终将会停止运动,粒子群形成了稳定的小生境,得到了邻域最优解,进而得到全局最优解。
(2)当粒子的历史最优和邻域最优不在同一个波峰下时,粒子xi进入pBesti所在波峰的“间距”内会导致这个“间距”(图4中2条虚线之间)变小,这样pBesti跳到pBestn,i所在波峰的概率会更小。在多步迭代后,pBesti和pBestn,i将会区分开来,vi将不会降为0,导致粒子xi永远振荡。然而,pBesti形成的群体和pBestn,i形成的群体将会趋于平衡,从而达到稳定的状态。pBestn,i形成的群体将会形成稳定的小生境,从而得到了全局最优解。
由上述讨论可知,该算法能促使粒子分布在多模问题的不同峰值上形成稳定的小生境。因此,相对于普通PSO,其得到全局最优解的概率更大。
2.3 TRNLPSO算法流程
TRNLPSO算法求解电力系统无功优化问题的流程如图5所示。

图5 TRNLPSO算法流程Fig.5 Flow chart of TRNLPSO
3 系统算例
国内某配电网系统如图6所示。该配电网有17个节点,其中节点1为发电机,(2,3)、(6,7)、(11,12)为变压器支路。4个无功补偿节点分别为节点2、3、7和节点11。设出线首端根节点的电压为恒定值1.0 kV。PV节点和平衡节点的电压上下限设置为1.1 kV及0.9 kV。PQ节点的电压上下限设置为1.05 kV及0.95 kV。4个无功补偿设备的上限分别为0.05、0.09、0.20、0.08,下限都为0,选取基准值为100 kvar。取系统的负荷水平,运行时间为3 600 h。选取SB=100MVA,系统运行时间以1 a计算,粒子群规模为20,最大迭代次数为600,C1与C2都为1.496 2,ω的初值取0.9。
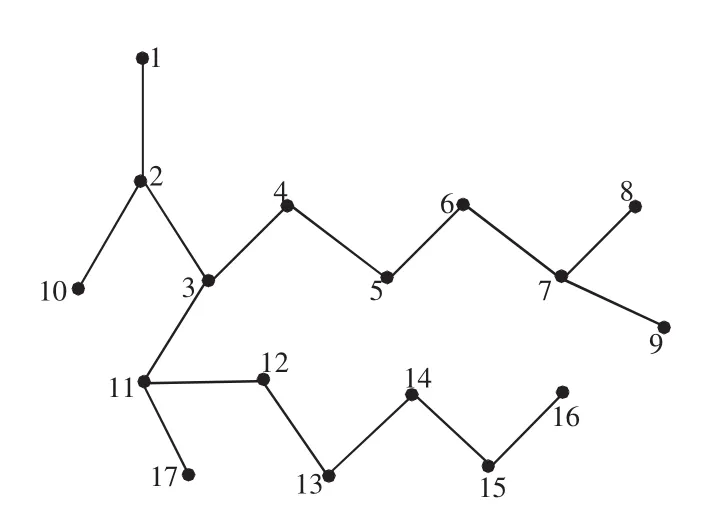
图6 某17节点系统Fig.6 System of 17-node
与运用PSO算法的系统相比较,运用TRNLPSO算法补偿后系统各个节点的电压水平有了明显的改善,如表1所示。

表1 PSO和TRNLPSO补偿后的各节点电压Tab.1 Node voltages after the compensation of PSO and TRNLPSOkV
PSO与TRNLPSO在电容的补偿容量上有着明显的区别,通过节点电压的对比可以看出,TRNLPSO在电容容量的取值上更具合理性。新增无功补偿方案如表2所示。

表2 新增无功补偿方案Tab.2 New reactive compensation program kvar
修正后系统的电价为600元/(MW·h),电容器的使用年限为10 a,电容器的价格为20 000元/Mvar。PSO与TRNLPSO补偿后的网损及综合费用如表3所示,由表3可以看出,经过TRNLPSO算法补偿后的综合费用和系统网损都明显低于经PSO算法补偿优化后的系统。

表3 不同算法优化结果比较Tab.3 Results of different algorithms
综上所述,在系统中加入补偿电容后,系统的节点电压、网损及综合费用都会有所改善。相对PSO算法而言,TPNLPSO算法优化效果更好。
4 结语
本文以系统的有功网损及投资设备的综合费用为优化目标,将节点电压越限和发电机无功出力越限采用罚函数的方式进行处理。对于已经建立的数学模型,本文采用基于拓扑环的小生境粒子群算法TRNLPSO进行补偿电容容量的选取优化。该算法无需任何小生境参数的先验知识,不但能够有效地提高算法的收敛精度,而且具有低计算复杂度的优点。同时可形成稳定的小生境,提高了获得最优解的概率。仿真实验表明,经过TRNLPSO优化算法优化后,系统的电压安全性得到了明显的提高。
[1]Dai Chaohua,Chen Weirong,Zhu Yunfang,et al.Seeker optimization algorithm for optimal reactive power dispatch[J].IEEE Trans on Power Systems,2009,24(3):1218-1231.
[2]何佳,吴耀武,娄素华,等(He Jia,Wu Yaowu,Lou Suhua,et al).基于SA_PSO的电力系统无功优化(Power system reactive power optimization based on simulated annealing particle swarm optimization algorithm)[J].电力系统及其自动化学报(Proceeding of the CSU-EPSA),2007,19(5):114-118.
[3]Venkatesh B,Sadasivam G,Khan M A.A new optimal reactive power scheduling method for loss minimization and voltage stability margin maximization using successive multi-objective fuzzy LP technique[J].IEEE Trans on Power Systems,2000,15(2):844-851.
[4]李滨,韦化,李佩杰(LiBin,WeiHua,LiPeijie).电力系统无功优化的内点非线性互补约束算法(Interior-point nonlinear algorithm with complementary constraints for reactive-power optimization)[J].电力自动化设备(Electric Power Automation Equipment),2010,30(2):53-58.
[5]AlRashidi M R,El-Hawary M E.Applications of computa-tional intelligence techniques for solving the revived optimal power flow problem[J].Electric Power System Research,2009,79(4):694-702.
[6]Liu Mingbo,Tso SK,Cheng Ying.An extended nonlinear primal-dual interior point algorithm for reactive-power optimization of large-scale power systems with discrete control variables[J].IEEE Trans on Power Systems,2002,17(4):982-991.
[7]Mantawy AH,AI-GhamdiM S.A new reactive power optimization algorithm[C]//IEEE Bologna Power Tech Conference,Bologna,Italy:2003.
[8]盛四清,远树平(Sheng Siqing,Yuan Shuping).基于粒子群算法的电力系统无功规划(Power system reactive power programming based on particle swarm algorithm)[J].电力科学与工程(Electric Power Science and Engineering),2009,25(6):16-19,28.
[9]张斌(Zhang Bin).基于粒子群算法的配电网无功补偿优化规划(Reactive power compensation of distribution network based on particle swarm optimization)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA),2010,22(2):157-160.
[10]刘自发,张建华(Liu Zifa,Zhang Jianhua).基于自适应小生境粒子群优化算法的电力系统无功优化(Reactive power optimization based on adaptive niche particle swarm optimization algorithm)[J].电力自动化设备(Electric Power Automation Equipment),2009,29(11):27-30.
[11]李惠玲,盛万兴,孟晓丽(Li Huiling,ShengWanxing,Meng Xiaoli).基于改进小生境遗传算法的配电网全网无功优化(General reactive power optimization of whole distribution network based on improved niche genetic algorithm)[J].电网技术(Power System Technology),2009,33(4):34-37,50.
[12]Kennedy J,Eberhart R.Particle swarm optimization[C]//IEEE International Conference on Neural Networks,Perth,Australia:1995.
[13]Li Xiaodong.Niching without niching parameters:particle swarm optimization using a ring topology[J].IEEE Trans on Evolutionary Computation,2010,14(1):150-169.
——以贵阳花溪公园为例

