风电场短期风速预测的MRA-SVM模型
杨亚兰,徐耀良,钟绍山,谢江媛
(上海电力学院电力与自动化工程学院,上海 200090)
开发和利用风能的主要形式是风力发电[1],随着风电容量占电力系统比重的日益增加,风电的出力预测对电网的影响不容忽视,而出力的预测主要取决于风速的预测。在时间尺度上,风速预测主要分为超短期、短期、中长期。超短期预测一般是30min以内的预测[2],用于对发电机的控制;中长期预测时间主要集中在未来几天至几个月,用于风电场的规划设计;短期预测是30min~72 h的预测,用于电力系统的功率平衡和调度、交易及暂态稳定评估等,其准确性直接影响电力系统在未来一段时间内的调度计划。
有关风速短期预测的问题,国内外学者进行了大量的研究,欧盟国家、美国等风电产业发展较早,大都开发出了专门的风电功率预报系统,预测时长可达到72 h,相应的预测成本也比较高[3]。我国的风力发电还处于初级阶段,预测的时间长度一般集中在30min~3 h时间段,预测误差范围[1~3]为25%~40%,预测方法的选择很大程度上影响着预测结果的精确性。
风速预测方法主要有物理模型法和时间序列模型法。物理模型法基于大量的气象、地表等因素和发电机的性能,其准确度主要依赖于气象模型,准确性的保证就必须在更长时间内不断校正,数据量大且不易获取,计算成本高,不适用于风速的短期预测;时间序列法基于统计学习理论,包括传统的持续预测法、卡尔曼滤波法、随机时间序列法、空间相关性法以及人工神经网络法,这些方法易于建模,并能够及时地预测[4~5]。但是,传统的时间序列法缺乏非线性处理能力,人工神经网络方法过多地强调克服学习错误而泛化能力不强,容易陷入局部最小化,使得预测推广能力较差[6~7];支持向量机SVM(support vector machine)作为继人工神经网络之后的又一种统计学习方法,对于处理具有小样本、非线性、高维数特点的序列有很好的适应性[8]。该算法利用最小化原则,引入了间隔概念,使得所建立的模型只由少数支持向量决定,减小了模型对于全部数据的依耐性[9]。
此外,影响风速变化的气象因素十分复杂,使得风电场风速呈非平稳变化的特点,风速v与风能E呈三次方关系[10],当风速频繁波动时,对风机的保养是极其不利的。然而,从频率特性来看,风速具有特殊的周期性,通过多分辨率分析MRA(multiresolution analysis),可将其看成是不同频率的分量的叠加,每个分量处于平稳变化状态,近似地呈周期变化,从而具有更强的预测性[10~11]。
对华东地区某风场的实际运行情况进行调研,发现预测风速的平均绝对误差高达40%,并且以人工估算为主。当风电容量不断增大时,这个误差会对电网产生不良影响。因此,选择有效的算法模型,提高风速预测的准确率,为调度部门提供可靠的数据基础具有现实的指导意义。本文通过对该风场实测风速数据建立多分辨率分析和支持向量机(MRA-SVM)模型,预测风电场未来4 h的风速值,实现了风速的多步预测,并与SVM方法进行比较,通过均方根误差RMSE(root mean square error)和平均相对误差MAPE(mean absolute percentage error)来评价模型的性能,取得了较好的预测效果。
1 MRA-SVM模型原理
为降低原始风速序列的非平稳性,增强其可预测性,对风速进行n层小波分解,所得细节系数为d1,d2,…,dn,近似系数为a1,a2,…,an,则x=a3+d1+d2+d3。对分解的各系数d1,d2,…,dn及an进行单支重构,得D1,D2,…,Dn及An。通过选择合理的核函数和惩罚因子等参数,对重构的风速序列分别进行SVM回归预测,并将单支预测风速进行叠加,即为原始风速序列的预测数据。模型流程如图1所示。

图1 模型流程Fig.1 Flow chart of the model
2 基于MRA-SVM的风速预测
2.1 模型样本
在模型的训练样本中,合理地选取输入变量对预测的准确度影响非常大。影响风速变化的因素有很多,如温度、气压、地表等大气因素,若选取这些变量作为输入变量,信息的获取不易,数据量大,运算复杂度增加。因此,风速的预测直接用历史风速序列来实现。虽然支持向量机模型的复杂度取决于支持向量的个数,并且输入量的维数越大,预测精度越高,但是输入维数过大会导致计算存储量大,计算时间变慢[12]。对于风速序列{x1,x2,…,xn},令{xi-m,xi-m+1,…,xi-1}为单个的输入变量,则模型的输入输出矩阵为

式中,m为输入变量维数。综合考虑计算时间、存储量、输入与输出之间的相关关系,本文取m=8。
本文采用华东地区某风场70m高空的实测风速数据,单位为m/s,该数据为平均每10min采集并存储1次。选取2012-01-09—2012-01-19期间34号风机的1 448个数据点,即1 440组输入作为模型的训练样本,对未来4 h的24个风速数据进行预测。
2.2 多分辨率分析
多分辨率分析由Mallat引入,从空间概念上形象地说明了小波的多分辨率特性,是信号的塔式多分辨率分析分解与重构的快速算法[13]。
一维情况下离散小波变换的Mallat算法的卷积表达式为

小波分解与重构的迭代过程如图2所示。
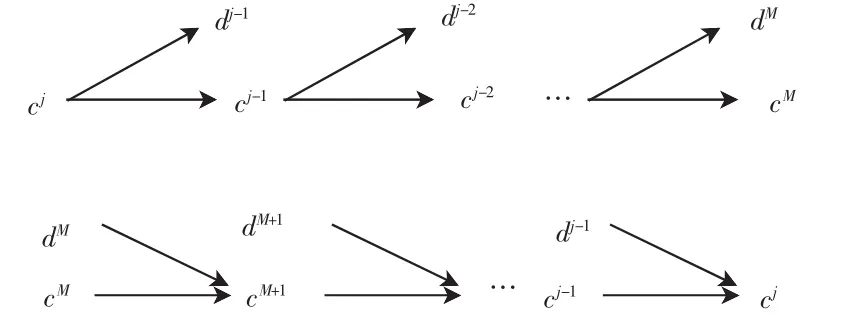
图2 迭代过程Fig.2 Iterative process
在对风速进行多分辨率分析时,要合理地进行小波基以及分解层数的选择。选择不同的小波基将得到不同的分量,而分解的级数过大则需要建立较多的SVM模型对各分量进行预测,各个模型都有一定的误差,导致最大误差变大;分解级数过小则不能将原信号不同频率的信号特征有效地提取出来[5]。因此,从预测计算的时间、算法的复杂度以及误差等方面考虑,并经过多次实验验证后,本文最终选择db3小波基对原始风速进行3层分解和重构,如图3所示。

图3 原始风速序列及小波分解Fig.3 Original wind speed and its wavelet decomposition
2.3 数据归一化处理
对样本进行预处理有利于加快算法的收敛速度,提高预测的精度,对训练集和测试集进行归一化处理[12],将原始数据规整在[0,1]范围内,则有

式中:x、y分别为归一化前、后的风速序列,x,y∈Rn;xmin=min(x);xmax=max(x)。归一化后,yi∈[0,1],i=1,2,…,n。由于多分辨率分解后的高频系数幅值较小,因此本文只对低频部分数据进行归一化,SVM预测后再进行相应的反归一化。
2.4 支持向量机
支持向量机由Vapnik首先提出,其主要思想是建立一个分类超平面作为决策曲面,使得正例和反例之间的隔离边缘被最大化。对于SVM回归预测,算法将实际问题通过非线性映射转换到高维的特殊空间,在高维空间中做线性回归来实现原空间中的非线性回归。SVM能保证机器具有良好的推广能力,同时也很好地解决了维数问题,而且其算法复杂度与样本维数无关。SVM体系结构[7,12]如图4所示。
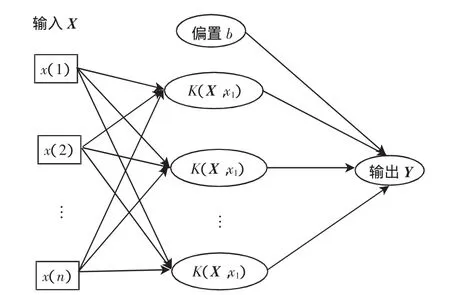
图4 SVM体系结构Fig.4 Structure of SVM system
对于训练样本集{(xi,yi),i=1,2,…,l},其中xi∈Rn为输入量;yi∈R为对应的输出;l为样本数量。SVM的估计函数为

式中:φ(x)为从输入控件到高维特征空间的非线性映射;ω为权向量;b为阈值。由最小化风险泛函得到目标函数,即
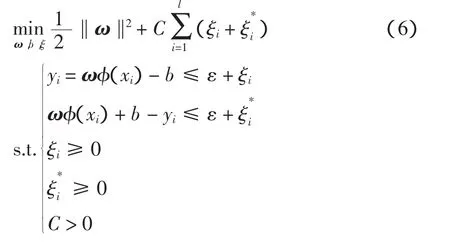
用Lagrange乘子法求解,相应的回归函数可变换为

式中:αi、αi*为Lagrange乘子;K(xi,xj)为核函数,且K(xi,xj)=φ(xi)φ(xj)。因此,不需要知道非线性映射φ的具体形式,只要利用核函数就可以进行非线性处理。对于函数回归问题,其决策函数就是核函数的线性组合,最终问题是寻找一组组合系数(αi-即可[14]。
支持向量机常用的核函数有线性核函数、多项式核函数、径向基核函数以及高斯核函数等。径向基核函数具有参数少、数值限制条件少的优点,可降低模型的复杂性。本文采用径向基RBF核函数,其函数表达式[14]为

对采集的原始风速数据只进行SVM训练,输出回归预测风速。训练集的实际风速与预测风速对比如图5所示。其中,预测均方根误差eMSE=14.34%,平均绝对百分比误差eMAPE=9.60%。对未来24 h的风速预测如图6所示。

图5 SVM回归预测风速Fig.5 Regression forecasting ofw ind speed with SVM

图6 未来4 h预测风速Fig.6 W ind speed in 4 hours
3 实例分析
3.1 MRA-SVM模型预测
对图5的原始风速数据进行MRA-SVM预测,当该模型的优化参数与SVM模型的相同时,用图1的模型结构对风速进行多分辨率分析处理,得到实际数据与回归预测数据的对比,如图7所示。其中,预测均方根误差eMSE=8.46%,平均绝对百分比误差eMAPE=5.85%。

图7 MRA-SVM回归预测风速Fig.7 Regression forecasting ofw ind speed with MRA-SVM
用训练后的MRA-SVM模型进行对未来4 h的风速进行预测。同时对预测数据与SVM方法进行比较,如图8所示。

图8 MRA-SVM与SVM模型的未来24 h风速Fig.8 W ind speed in 24 hours with MRA-SVM and SVM
3.2 评价指标及适应性分析
为了衡量预测风速的精确度,评价MRA-SVM模型的性能,本文采用的均方根相对误差eRMSE和平均绝对百分比误差eMAPE分别表示为式中:n为样本总量;Xi和X^i分别为第i个点的实际风速和预测风速。
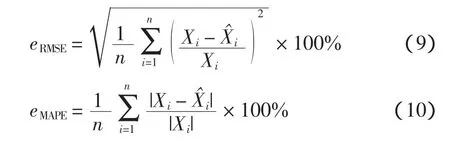
对比2种模型的评价指标,即训练集与预测集的均方根误差和平均绝对误差,结果如表1所示。由表1可知,运用MRA-SVM模型预测风速的eRMSE和eMAPE分别为10.36%、8.81%,与SVM方法的预测指标相比,明显地提高了风速的预测精度。

表1 34号风机的SVM及MRA-SVM模型预测指标Tab.1 Prediction index with SVM and MRA-SVM of generator No.34%
为验证模型是否具有普遍适应性,本文对风场不同的风机在不同时段的风速数据进行实验,证明回归预测模型曲线均能较好地跟踪实际风速曲线。对35号风机的未来4 h的风速进行预测的评价指标如表2所示,由表2可知,用MRA-SVM模型对风速预测的eRMSE和eMAPE分别为16.98%、11.47%,精确度要高于SVM模型的22.18%和17.27%。

表2 35号风机的SVM及MRA-SVM模型预测指标Tab.2 Prediction index with SVM and MRA-SVM of generator No.35%
通过对不同的数据进行多次实验证明,该模型能提高预测的精确性,普遍适用于风电场的短期风速预测。
4 结语
针对风电场随机波动的风速,为提高其预测的准确性,本文运用了MRA-SVM模型对原始风速进行小波分解,降低风速的非平稳性,再运用SVM方法对分解后的近似系数和细节系数分别进行回归预测并叠加,以此来提高模型的预测能力。通过对风速进行多分辨率分析,用平均绝对百分比误差和均方根误差2个指标来评价,预测结果表明,该方法较单独的SVM方法相比预测效果良好。与此同时,本文对不同的采样数据进行仿真,验证了模型的普遍适用性。
[1]杨秀媛,肖洋,陈树勇(Yang Xiuyuan,Xiao Yang,Chen Shuyong).风电场风速和发电功率预测研究(Wind speed and generated power forecasting in wind farm)[J].中国电机工程学报(Proceedings of the CSEE),2005,25(11):1-5.
[2]戴浪,黄守道,黄科元,等(Dai Lang,Huang Shoudao,Huang Keyuan,et al).风电场风速的神经网络组合预测模型(Combination forecasting model based on neural net works for wind speed in wind farm)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA),2011,23(4):27-31.
[3]罗文,王莉娜(LuoWen,Wang Lina).风场短期风速预测研究(Short-term wind speed forecasting for wind farm)[J].电工技术学报(Transactions of China Electrotechnical Society),2011,26(7):68-74.
[4]李元诚,方廷健,于尔铿(LiYuancheng,Fang Tingjian,Yu Erkeng).短期负荷预测的支持向量机方法研究(Study of support vector machines for short-term load forecasting)[J].中国电机工程学报(Proceedings of the CSEE),2003,23(6):55-59.
[5]师洪涛,杨静玲,王金梅,等(Shi Hongtao,Yang Jingling,Wang Jinmei,et al).基于小波-BP神经网络的短期风电功率预测方法(A short-term wind power prediction based on wavelet decomposition and BP neural network)[J].电力系统自动化(Automation of Electric Power Systems),2011,35(16):44-48.
[6]黄文杰,傅砾,肖盛(HuangWenjie,Fu Li,Xiao Sheng).采用改进模糊层次分析法的风速预测模型(A predictive model of wind speed based on improved fuzzy analytical hierarchy process)[J].电网技术(Power System Technology),2010,34(7):164-168.
[7]吴国旸,肖洋,翁莎莎(Wu Guoyang,Xiao Yang,Weng Shasha).风电场短期风速预测探讨(Discussion about short-term forecast of wind speed on wind farm)[J].吉林电力(Jilin Electric Power),2005,(6):21-24.
[8]Sangitab P,Deshmukh SR.Use of support vector machine for wind speed prediction[C]//International Conference on Power and Energy Systems.Chennai,India:2011.
[9]Zeng Deliang,Liu Yu,Liu Jiwei,et al.Short-term wind speed forecasting based on wavelet tree decomposition and support vector machine regression[J].Advances in Automation and Robotics,2011,123(2):373-379.
[10]张彦宁,康龙云,周世琼,等(Zhang Yanning,Kang Longyun,Zhou Shiqiong,et al).小波分析应用于风力发电预测控制系统中的风速预测(Wavelet analysis applied to wind speed prediction in predicate control system of wind turbine)[J].太阳能学报(Acta Energiae Solaris Sinica),2008,29(5):520-524.
[11]王晓兰,王明伟(Wang Xiaolan,WangMingwei).基于小波分解和最小二乘支持向量机的短期风速预测(Short-term wind speed forecasting based on wavelet decomposition and least square support vector machine)[J].电网技术(Power System Technology),2010,34(1):179-184.
[12]彭春华,刘刚,孙惠娟(Peng Chunhua,Liu Gang,Sun Huijuan).基于小波分解和微分进化支持向量机的风电场风速预测(Wind speed forecasting based on wavelet decomposition and differential evolution-support vector machine for wind farms)[J].电力自动化设备(Electric Power Automation Equipment),2012,32(1):9-13.
[13]刘辉,田红旗,李燕飞,等(Liu Hui,Tian Hongqi,LiYanfei,et al).基于小波分析法与滚动式时间序列法的风电场风速短期预测优化算法(Short-term forecasting optimization algorithm for wind speed from wind farms based on wavelet analysis method and rolling time series method)[J].中南大学学报:自然科学版(Journal of Central South University:Science and Technology),2010,41(1):370-375.
[14]Zhang Huaqiang,Wang Xinsheng,Wu Yinxiao.Application of an improved SVM algorithm for wind speed forecasting[J].Future Intelligent Information Systems,2011,86(1):333-340.

