实际负荷变化模式下的静态电压稳定分析

伍利，南海鹏，姚李孝

（西安理工大学水利水电学院，西安 710048）

由于环境和经济的因素，电力系统运行越来越靠近其稳定极限[1～4]。对于一个实际系统而言，负荷增长受很多因素的影响，通常在电力系统分析中，可以将负荷的变化看作不确定的扰动。在计算静态电压稳定裕度指标的过程中，选择负荷增长的模式是一个难点，不同的负荷增长模式对静态电压稳定裕指标大小的影响很大。在采用负荷等比例等功率因数增长的模式下，整个系统的静态电压稳定裕度可能受制于这些电压稳定弱节点集。这一方面反映了真实系统中的薄弱母线和薄弱区域，另一方面，这样的结果还不能给出一个完全贴近系统真实情形的裕度值，因为在实际系统中，负荷往往并非按等比例等功率因数方式增长。更合理的模式应参考实际电网的负荷预测数据，由负荷预测数据给出一个合理的负荷增长方向，根据负荷预测增长方向计算的负荷裕度应该比等比例负荷增长模式下的负荷裕度更加贴近电网运行实际情况[4～8]。

系统的负荷裕度为当前运行点的负荷水平和电压稳定极限点的负荷水平之间的差值，即系统所处的运行状态不同，系统的负荷裕度不同。从基值开始的不同负荷增长率叫做负荷增长模式或负荷变化方向LD（load direction），负荷增长模式是不可控制的。已有的研究成果大多只是简单分析了负荷增长对电压稳定的影响，没有对负荷增长模式对电压稳定裕度的影响进行细化研究。根据系统当前的运行状态及该地区负荷的增长模式分析的电压稳定才能对系统的实际运行作指导。通常一天的负荷变化由日负荷曲线表示，在静态电压稳定分析中用日负荷曲线识别负荷的增长模式，就能预测当前系统运行状态下的负荷裕度。

本文以历史负荷数据为依据，对负荷数据进行模糊聚类分析，然后用改进的BP神经网络进行负荷预测，确定负荷的增长模式及负荷的变化方向，在此基础上用连续潮流法对IEEE30进行电压稳定研究分析，获得系统在当前运行状态及一定负荷增长模式下的系统电压稳定裕度。

1 负荷增长

负荷增长模式或“方向”定义为系统中每个节点负荷增长的方式，即

式中：PDi0、QDi0分别为节点i（i=1，2，…，n）的有功、无功基础负荷；PDi、QDi分别为节点i的有功、无功负荷；λ为负荷增长因子，表示有功和无功以相同比率增长，也就是负荷在相同的功率因数下增长；KDi为节点有功和无功负荷增长的方向标量，并且对电压稳定有影响。

传统方法算法中，负荷以相同的比例增长[7～10]。在考虑负荷增长模式的电压稳定研究中，潮流等式被修正为含有负荷增长因子及负荷方向的标量，即

式中：KD为负荷变化方向矢量，在文献[3]中，节点2和节点3的基础负荷分别为21.70+j12.7MV和94.2+j19.00MV。在节点2取KD2=0.217+j0.127；在节点3取KD3=0.942+j0.19。也就是对于一个负荷因子λ，负荷节点将以相同的百分数从基值增长，但各节点的负荷增长模式不同。文中对以相同负荷增长率的称其为相同的负荷方向或传统的负荷方向。

2 预测模型及算法

2.1 形成预测样本

计算静态电压稳定裕度指标的短期负荷预测是电力系统安全经济运行的基础，负荷预测受到各种因素的影响，如气象因素、日类型和突发事件等。气象因素有气温、湿度、降雨量和风速等，日类型包含有一般工作日、双休日和特殊节假日。对这些相关因素的规范处理，可提高短期负荷预测的精度。

设预测日的n个样本集为X=[x1，x2，…，xn]T，每个样本xj有m个特征指标xj=[xj1，xj2，…，xjm]T（j=1，2，…，n），则n个样本的特征指标为

样本与样本之间的模糊相似关系矩阵为

在一定条件下样本集X通过模糊关系矩阵R进行分类。对X=[x1，x2，…，xn]T分成c类（2≤c≤n），则c个聚类中心向量为

vi（i=1，2，…，c）对应的m个指标是该类元素所对应的平均值，vi=（vi1，vi2，…，vim]，则

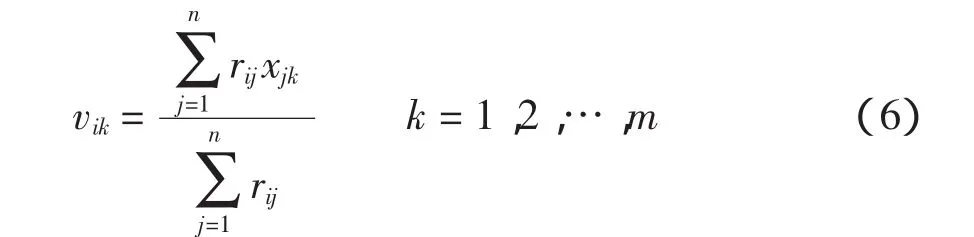
式（6）的分母相当于第i类的元素个数，而分子为第类的所有元素第k个指标和。为了获得一个最佳的模糊分类，可通过模糊聚类算法迭代运算，优选一个最好的模糊分类，即

式中：q=2；‖xj－vi‖为Euclid距离。

2.2 预测日归类

样本进行分类后，对预测日进行归类，归类时需计算预测日与样本类别的欧氏距离，即

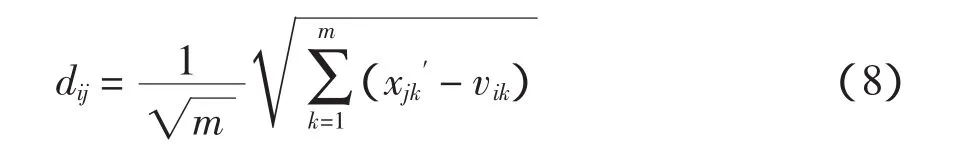
式中，xjk′为预测日的特性指标，以最短欧氏距离作为预测日的归类判别，然后以BP网络进行预测。

2.3 改进BP神经网络预测模型

BP算法是一个非线性梯度最优问题，存在收敛速度慢和易陷入局部极小值。改进的BP神经网络[6]采用附加动量法以改变每次迭代的前进方式来提高收敛速度。附加动量算法是在梯度下降的基础上，引入动量因子η（0＜η＜1）能使网络收敛得更快，并且可避免局部极小值的出现。

式中：x（k+1）、x（k）分别为第k+1、k次迭代时的权值向量；α为学习速率。

该方法所加入的动量项是指在网络每次的权值和阈值改变量中加入前一次的改变量，并且动量因子η越大，同一梯度方向上的动量也越大。实质上动量项相当于阻尼项，它减少了学习过程的振荡趋势，改善了收敛性。上述表明在保证算法稳定的同时，附加动量法的收敛速率较快，学习时间较短。

3 电力系统日负荷曲线及负荷预测

3.1 日负荷曲线

实际的系统负荷是随时间变化的，其规律可用负荷曲线来描述。常用的负荷曲线有日负荷曲线和年负荷曲线。日负荷曲线是以1 d（24 h）为周期的负荷变化。随着我国电力市场的进一步发展，日负荷曲线对电力系统的运行非常重要，它是安排日发电计划和确定系统运行方式的重要依据。从负荷曲线可知，日负荷会出现早高峰和晚高峰，冬季的早高峰出现在10：00左右，晚高峰出现在19：00左右。而夏季的早高峰略有提前，出现在9：00左右，午后的负荷高峰在16：00左右，晚高峰略有推迟，出现在21：00左右。早高峰低于午后高峰和晚高峰，最大负荷出现在晚高峰时段。各高峰之间负荷变化有明显的波动，在早、晚高峰之间负荷持续在高峰。

3.2 负荷预测

一个地区的负荷变化取决于多种因素，如气温、人的行为、负荷类型、关税等等，这可从不同地区的实际日负荷需要反映出来。在这些因素的影响下，不同地区的电力系统的短期负荷会出现较大的差异[6～11]。本文先将影响负荷变化的主导因素进行分析，也就是对气象因素和日类型与负荷之间的关系进行量化处理，建立模糊相似矩阵。采用模糊聚类方法对夏季负荷类型进行分析并形成预测样本，然后对预测日以最短欧氏距离进行归类，再对1 d的24点负荷逐点建立BP神经网络预测模型，用附加动量和变学习速率的BP算法训练样本，最终得到预测日24点的负荷值，预测结果如表1所示。

表1 负荷预测结果Tab.1 Resultsof load forecasting

从表1可知，所有的相对误差小于3%。相对误差小于2%的点有23个，最大相对误差为2.412%，最小相对误差为－0.058%，平均相对误差0.317%，预测值符合实际负荷变化。

在经典的电压稳定研究中，应用相同的负荷方向不符合实际的电力系统，在日负荷的不同时间每一节点的负荷增长模式由日负荷曲线确定，即

式中：Pm，t+1为t+1时刻的负荷预测数据；Pm，t为t时刻的负荷预测数据。不同时段的负荷变化如表2所示，Pm，max为Pm，t的最大值。

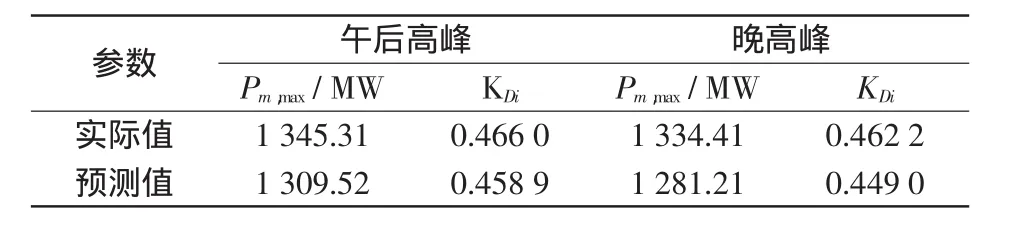
表2 不同时段负荷变化方向Tab.2 Load variation direction in different time

由于负荷预测只提供有功功率预测，以维持功率因数恒定，在计算中假定无功功率也以相同的系数增加。因此，在连续潮流等式（2）中系统负荷节点的无功率负荷增量由式（1）获得。

4 结果分析

本文以IEEE30系统为例，如图1所示，分别以传统负荷增长模式和预测负荷增长模式将增长负荷在可利用的发电机间进行分配，以CPF进行潮流分析，计算系统的负荷裕度，获得各节点的PV曲线。选取在负荷增加时节点电压较弱并对负荷变化敏感的节点3、4、6、7、9和节点10进行比较[11～16]，如图2和图3所示。

图1 IEEE30测试系统Fig.1 IEEE30 test system

图2 传统负荷增长时较弱节点的电压Fig.2 Bus voltage of weak nodes with conventional load grow th

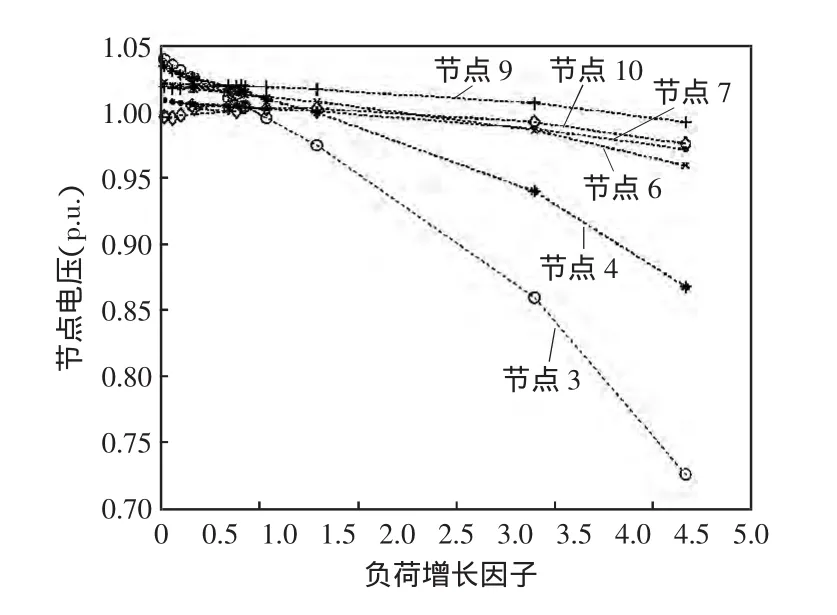
图3 基于预测负荷增长时较弱节点的电压Fig.3 Bus voltage of weak nodes based on forecasted load grow th

由图2和图3可知负荷增长模式不同对较弱节点的电压及系统负荷裕度的不同影响，节点6、7、9、10电压轨迹变化显著。在图2中传统相同负荷增长模式下负荷增值较大，负荷增长因子小，潮流结果变化显著，在PV曲线接近鼻型区域损耗增加较快，因此负荷裕度小。在图3中预测负荷增长模式负荷增值相对较小，负荷增长因子大，潮流结果开始变化较小，在接近其裕度极限时，电压下降加快，电压下降了8.2%，但负荷裕度相比提高了55%。

表3给出了系统不同运行阶段的LD及其负荷裕度，可知在晚高峰时，负荷裕度高于在午后高峰，主要是由于晚高峰时段各负荷节点的负荷功率已经处于高峰，系统再能承受的的负荷增长很有限。

表3 不同LD的负荷裕度比较Tab.3 Load margin comparison of different LD（p.u.）

5 结论

本文以采集的典型日负荷曲线预测未来时段内负荷的变化，应用CPF对以此确定的负荷增长模式进行电压稳定分析。以实际负荷增长模式评估静态电压稳定的特点。

（1）以实际历史负荷样本预测负荷增长模式能真实反映电力系统负荷增长方式。

（2）采用模糊聚类和改进的BP神经网络模型预测的负荷增长相对误差小于3%，符合实际的负荷增长规律。

（3）与传统分析静态电压稳定分析相比，系统所处的运行状态不同，系统可承受的负荷增长不同，因而系统的负荷裕度不同；不同负荷增长模式使系统各节点的PV曲线呈现不同的变化。在系统的峰荷时段，系统能承担的负荷增长是有限的。以本文方法对系统的不同运行状态的电压稳定分析，对电力系统调度有一定的实际指导意义。

[1]Nagao T，Tanaka K，Takenaka K．Development of static and simulation programs for voltage stability studies of bulk power system[J]．IEEE Trans on Power Systems，1997，12（1）：273－281．

[2]Sode Y A，Mithulananthan N，Lee K Y．Effect of realistic load direction in static voltage stability study[C]//IEEE/PES Transmission and Distribution Conference and Exhibition.Dalian，China：2005．

[3]Green S，Dobson I，Alvarado F L．Sensitivity of loading margin to voltage collapse with respect to arbitrary parameters[J]．IEEE Trans on Power Systems，1997，12（1）：262-272．

[4]Sode Y A，Mithulananthan N．Maximizing static voltage stability margin in power systems using a new generation pattern[J].Australian Journal of Electrical&Electronics Engineering，2005，2（3）：255-261．

[5]栗然，曹磊，李莉，等（LiRan，Cao Lei，Li Li，et al）.影响电力系统短期负荷预测因素的权重分析方法（Analysis for weights allocation with influence factors in power system short-term load forecasting）[J].华北电力大学学报（Journal of North China Electric Power University），2007，34（5）：32-37．

[6]姚李孝，宋玲芳，李庆宇，等（Yao Lixiao，Song Lingfang，LiQingyu，et al）．基于模糊聚类分析与BP网络的电力系统短期负荷预测（Power system short-term load forecasting based on fuzzy clustering analysis and BP neural network）[J].电网技术（Power System Technology），2005，29（1）：20-23．

[7]黎灿兵，李晓辉，赵瑞，等（LiCanbing，LiXiaohui，Zhao Rui，et al）．电力短期负荷预测相似日选取算法（A novel algorithm of selecting similar days for short-term power load forecasting）[J]．电力系统自动化（Automation of Electic Power Systems），2008，32（9）：69-73．

[8]黎灿兵，杨朋，刘玮，等（LiCanbing，Yang Peng，Liu Wei，et al）．短期负荷预测中考虑夏季气温累积效应的方法（An analysis of accumulative effect of temperature in short-term load forecasting）[J]．电力系统自动化（Automation of Electric Power Systems），2009，33（9）：96-99．

[9]高新波．模糊聚类分析及其应用[M].西安：西安电子科技大学出版社，2004.

[10]陈得治，张伯明，方兴（Chen Dezhi，Zhang Boming，Fang Xing）．节点注入功率模式对电压稳定裕度的影响（Effect nodal injection power mode on voltage stability margin）[J]．电网技术（Power System Technology），2009，33（2）：62-67，72.

[11]随慧斌，赵建国，李可军，等（SuiHuibin，Zhao Jianguo，LiKejun，et al）．考虑不均衡区域负荷增长的在线电压稳定评估（On-line voltage stability assessment considering uneven growth of regional load）[J]．电力自动化设备（Electric Power Automation Equipment），2011，31（3）：57-61．

[12]赵晋泉，张伯明（Zhao Jinquan，Zhang Boming）．连续潮流及其在电力系统静态稳定分析中的应用（Summarization of continuation power flow and its application in static stability analysis of power system）[J]．电力系统自动化（Automation of Electric Power Systems），2005，29（11）：91-97．

[13]熊宁，程浩忠，李曼丽，等（Xiong Ning，Cheng Haozhong，LiManli，et al）．基于可信度区间的静态电压稳定性评价（A static voltage stability evaluation method based on confidence intervals）[J]．电力系统自动化（Automation of Electric Power Systems），2009，33（9）：16-19．

[14]顾伟，蒋平，唐国庆（GuWei，Jiang Ping，Tang Guoqing）．提高电力系统小扰动稳定性的最优分岔控制策略（Optimal bifurcation control to improve small-signal stability of power systems）[J]．电力自动化设备（Electric Power Automation Equipment），2007，27（10）：29-33．

[15]伍利，古婷婷，姚李孝（Wu Li，Gu Tingting，Yao Lixiao）．基于改进连续潮流法的静态电压稳定分析（Static voltage stability analysis based on improved continuation power flow）[J]．电网技术（Power System Technology），2011，35（10）：99-103．

[16]张尧，张建设，袁世强（Zhang Yao，Zhang Jianshe，Yuan Shiqiang）．求取静态电压稳定极限的改进连续潮流法（Improved continuation power flow algorithm for obtaining the limit of static voltage stability）[J]．电力系统及其自动化学报（Proceedings of the CSU-EPSA），2005，17（2）：21-25．