基于人工蜂群算法的分布式电源规划

周文越，吕飞鹏，廖小君

（1.四川大学电气信息学院，成都 610065；2.四川省电力职业技术学院，成都 610072）

随着社会不断进步，传统能源逐渐枯竭，世界各国对环保问题日益重视，因此需要一种环保、灵活的方式来解决能源问题[1]。在这些背景下，分布式电源应运而生。目前，大电网与分布式电源相结合的方式被世界许多电力专家公认为是能够降低能耗、节省投资、提高电力系统灵活性和可靠性的主要方式，这也是21世纪电力工业的主要发展方向。

分布式电源DG（distributed generation）指的是为了满足一些特殊用户的需求，在确保已有的配电网的安全和经济运行的前提下设计和安装的在用户处或其附近的小型发电机组（一般小于30 MW）、或安装在用户附近以使得负荷的供电可靠性以及电能质量都得到增强、或者由于就地应用热电联产使得效率得到提高的发电形式[2]。

当规划方案中出现大量的分布式电源时，随机变量会大大加大电力系统的复杂性。传统的规划方法很难解决包含分布式电源的配电网规划问题。近年来，国内外学者对分布式电源的规划研究取得了一定的成果。在模型方面，文献[3]以利益/成本比最大为目标函数，利用遗传算法对分布式电源的位置和容量进行了优化；文献[4]在考虑多个目标（损耗成本、缺电成本、网络升级成本、电能质量成本和电能成本）的前提下进行规划；文献[5]以电网稳定为目标建立规划模型，在算法方面，分布式电源的选址和定容是一个具有不确定性、非线性等特点的组合优化问题；文献[6]在给定分布式电源容量情况下，采用解析法研究了配电网中辐射线路上分布式电源的最优安装位置；文献[7]基于改进的免疫克隆选择算法进行模型求解；文献[8]采用自适应变异粒子群算法对分布式电源选址和定容的模型进行计算。

本文以分布式电源投资商收益最大为目标，建立了规划模型。针对分布式电源规划模型离散、非线性的特点，采用人工蜂群算法进行模型求解，并根据模型要求适当改进了算法。

1 分布式电源规划模型

本文考虑分布式电源投资商收益最大建立目标函数。归一化目标函数具体描述为

式中，Cp为折算到每年的售电费用，是分布式电源发出的电能卖给电网公司所赚取的费用，即

CDG为折算到每年分布式电源的安装、运行、维护费用，即

式中：n为分布式电源数量；Ce为单位电价，元/（kW·h）；Tmax为年最大负荷利用小时数，根据分布式电源的类型以及实际运行状态，取不同的值，并保持恒定；lj为对应分布式电源的容量系数；Pj，DG为对应分布式电源额定有功功率；r为固定年利率；m为规划年限；Cj，DG为第j个分布式电源的安装成本，元/kW，包括原动机成本、发电机成本和无功补偿设备成本；Cj，DM为分布式电源的固定维护成本，元/（kW·h）。式（3）括号中的第1项将分布式电源的固定成本按规划年限折算到规划年限内每年等额支付金额。

约束条件如下。

（1）潮流约束为

式中：i和j为节点编号；PDG，i为节点i安装的分布式电源有功功率；n1为节点数；PL，i为节点i负荷有功功率；QDG，i为节点i安装的分布式电源无功功率；QL，i为节点i负荷无功功率；Ui和Uj为节点电压；Gij和Bij为相应支路的电导和电纳；δij为节点i和节点j电压的相角差。

（2）节点电压约束为

（3）支路功率约束为

式中：Pij为ij支路传输功率为ij支路传输功率上限。

（4）分布式电源安装台数约束为

2 人工蜂群算法

2.1 算法原理

2005年Karaboga成功地将蜜蜂觅食原理运用于数值优化问题上，提出了人工蜂群算法[9]。作为一种典型的群居生物，单个蜜蜂的智慧是有限的，但是当一群蜜蜂聚在一起时，就会表现出惊人的智慧。不管在什么环境下，蜜蜂总是可以在蜂巢周围找到食物最丰富的食物源。

在人工蜂群算法中，每个食物源对应优化问题的一个可行解，食物源的丰富程度对应可行解的适应度值。在算法开始阶段，所有的蜜蜂皆为侦察蜂，在蜂巢附近寻找食物源，之后，引领蜂会对食物源领域进行搜索，并比较搜索前后食物源的丰富程度，选择较丰富的食物源作为采集目标。当引领蜂完成搜索后，它们会回到蜂巢，并在舞蹈区将自己掌握的食物源信息与其他蜜蜂分享，跟随蜂会根据食物源的丰富程度以一定概率选择引领蜂进行跟随。当然，食物源越丰富，被选择的概率也就越大。

2.2 算法步骤

在人工蜂群算法中，蜂群的觅食行为与优化问题之间存在的关系如表1所示。

表1 蜂群的觅食行为与优化问题对应关系Tab.1 Relationship between bee colony foraging behavior and function optimization

将可行解表示为一维向量，即

式中，N为解向量的维数，j∈{1，2，…，D}，D为种群数量。初始化时，随机产生可行解的公式为

蜜蜂对每一个蜜源进行领域搜索，产生一个新的位置，其公式为

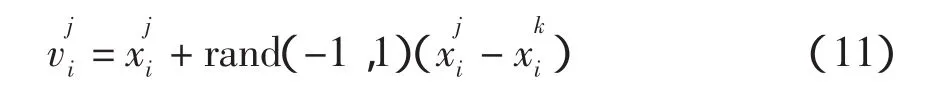
式中，fitj为第j个解的适应度，也即第j个蜜源的丰富度。

跟随蜂根据转移概率选择引领蜂进行跟随，并进行领域搜索，选择较为丰富的蜜源作为采集目标。舍去那些超过搜索次数而没有更新的蜜源，侦察蜂重新进行搜寻。重复上述过程直到达到最大循环次数。

2.3 人工蜂群算法下的分布式电源规划

为了将人工蜂群算法运用于分布式电源规划，首先需要对分布式电源安装信息进行编码，蜂群算法中的各种操作将围绕编码进行。此次算例只考虑微型燃气轮机和风力发电2种分布式电源，且风力发电要求集中接入，因此只有一个节点可安装风力发电机，可用2个编码表示其安装信息，即

式中：a1为安装位置信息，其大小为风力发电机安装节点的编号；a2为风力发电机容量信息，其大小为风力发电机的安装台数。对于微型燃气轮机，用n个编码表示安装信息，即

式中：e为微型燃气轮机待安装节点的数量，每一个bi对应一个网络节点上微型燃气轮机的安装台数。将C1、C2组合便可得到总的编码为

式（11）是对于控制变量取实数编码时的一般形式，如果采用式（11）进行领域搜索，则将大量进行取整操作，且搜索易超出范围，搜索效率不高。而本文采用整数编码，考虑到编码都为整数，且数值不大，进行领域搜索时可以保证搜索结果依旧为整数，且不易超出范围。搜索公式为

例如，在给学生讲解《妈妈的爱》这篇诗歌的时候，教师可以让学生有感情地朗读，读出妈妈对孩子无私的关爱以及孩子对妈妈的感恩之情。然后，教师可以对学生进行启发，引导学生理解诗歌的具体内容，感受修辞手法的运用，激发学生对母亲的感恩之情。最后，教师可让学生进行写作练习，自己创作简单朴实的诗歌来表达对母亲的爱，以此来培养学生的写作能力，达到促进学生的阅读和写作能力双向提高的目的。

式中：i随机生成；t为1或－1，且随机生成。

另外，在进行侦察操作时，对那些即使达到最大搜索次数的最优可行解不进行更新。

运用人工蜂群算法解决分布式电源规划的具体步骤如下。

步骤1运用式（10）产生D个初始解，且取整，对每个初始解进行校验，如果解不满足约束条件式（6）～式（8）中任意一个，则舍去并重新产生一个直到满足约束条件。

步骤2计算每个可行解的适应度，运用式（16）对每一个可行解进行领域搜索。如果搜索到的可行解满足约束条件且其适应度的值大于原始可行解的适应度值，则替换原始可行解；反之则保持原始解不变。

步骤3按适应度大小，从大到小，用轮盘赌方法选择可行解，并对每个被选中的可行解进行领域搜索，选取适应度值较大的解。

步骤4放弃超过n次迭代而没有更新的解，并产生新解。

步骤5重复上述步骤，直到达到迭代次数。

3 算例分析

本文所选的算例是一个具有69个节点、68条支路的10 kV配电网，如图1所示。节点0为变电站节点，其电压恒定为12.66 kV，其余均为负荷节点。本次规划只考虑风力发电机和微型燃气轮机两种分布式电源，具体成本参数见表2。在配电网中，圆圈表示微型燃气轮机待安装位置，方形表示风力发电机待安装位置，为维持风电场一定的规模，风电机组只允许从单节点集中接入。微型燃气轮机单机额定功率为100 kW，每个节点允许安装的最大台数为10台。风力发电机的单机额定功率为600 kW。

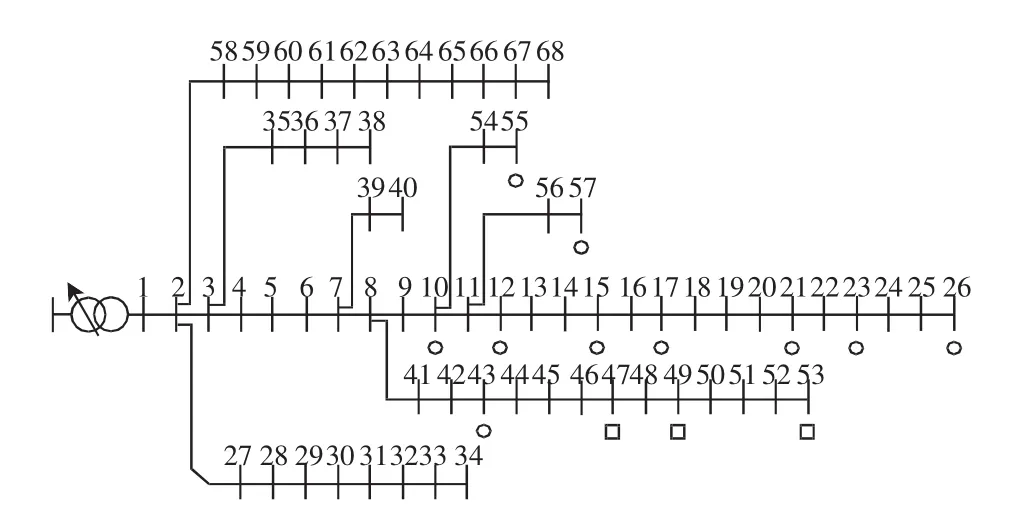
图1 配电网示意Fig.1 Schematic diagram of distribution system

表2 各类型分布式电源参数Tab.2 Parameters of distributed generators

电网规划期限为10 a，忽略负荷增长，风力发电机容量系数为0.5，微型燃气轮机容量系数为1，最大负荷利用小时数Tmax为4 600 h。蜂群群体大小为100，侦察蜂的数量为10个，最大迭代次数为100次。人工峰群算法的进化过程如图2所示，其最优方案的结果如表3和表4所示。

图2 人工蜂群算法进化过程Fig.2 Convergence curve of artificial bee colony algorithm

表3 最优方案的费用Tab.3 Cost of the optimal case 万元

表4 最优分布式电源的安装方案Tab.4 Optimal case of the allocation and siting of distributed generators 台

从图2中可以看出，算法的速度非常快，在第40次迭代左右达到最优值。

在约束条件中，分布式电源的最大安装台数为30台。在最终方案中，分布式电源的安装台数为24台，接近最大允许安装台数，这是因为，当分布式电源的安装台数达到一定数量时，其带来的收益要大于分布式电源的投资运行成本。此外，虽然分布式风力发电机的安装容量较大，投资费用较高，但运行维护费用远远低于微型燃气轮机。

4 结语

本文采用了人工蜂群算法，对69节点的配电网络进行了基于独立发电商收益最大的优化规划。所采取的算法收敛性好，编程简单，计算速度快，提出的模型对分布式电源的规划问题有一定的参考价值。但本文所考虑的规划模型缺少对配网升级的考虑，且对于风力发电出力，按恒定出力计算，给出容量系数，未考虑其随机特性，这些将在后续研究中进行完善。

[1]于建成，迟福建，徐科，等（Yu Jiancheng，Chi Fujian，Xu Ke，et al）.分布式电源接入对电网的影响分析（Analysis of the impact of distributed generation on power grid）[J].电力系统及其自动化学报（Proceedings of the CSUEPSA），2012，24（1）：138-141.

[2]王敏，丁明（WangMin，DingMing）.含分布式电源的配电系统规划（Distribution network planning including distributed generation）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2004，16（6）：5-8，23.

[3]Teng Jen-Hao，Luor Tain-Syh，Liu Yi-Hwa.Strategic distributed generator placements for service reliability improvements[C]//IEEE Power Engineering Society Summer Meeting，Chicago，USA：2002.

[4]CelliG，Ghiani E，Mocci S，et al.A multi-objective formulation for the optimal sizing and siting of embedded generation in distribution networks[C]//IEEE Power Tech Conference Proceedings，Bologna，Italy：2003.

[5]刘智昱，黄伟（Liu Zhiyu，HuangWei）.基于稳态分析和区间层次分析法的分布式电源最佳位置确定方法（A method for optimal layout of distributed generations based on steady-state analysis and interval analytic hierarchy process）[J].电网技术（Power System Technology），2011，35（11）：57-61.

[6]Wang Caisheng，Nehrir M H.Analytical approaches for optimal placement of distributed generation sources in power systems[J].IEEE Trans on Power Systems，2004，19（4）：2068-2076.

[7]徐玉琴，李雪冬（Xu Yuqin，LiXuedong）.基于改进免疫克隆选择算法的含分布式电源配电网规划方法（An improved immune clonal selection algorithm based planning method for distribution network with distributed generators）[J].电网技术（Power System Technology），2010，34（8）：97-101.

[8]叶德意，何正友，臧天磊（Ye Deyi，He Zhengyou，Zang Tianlei）.基于自适应变异粒子群算法的分布式电源选址与容量确定（Siting and sizing of distributed generation planning based on adaptive mutation particle swarm optimization algorithm）[J].电网技术（Power System Technology），2011，35（6）：155-160.

[9]Karaboga D.An idea based on honey bee swarm for numerical optimization[R].Kayseri，Turkey：Erciyes University，2005.