基于LCC理论的变电站主变容量及台数选择

邓道福，姚建刚，赵军毅，毛田，康童，孔奎

（1.湖南大学电气与信息工程学院，长沙 410082；2．湖南湖大华龙电气与信息技术有限公司，长沙 410082；3．长沙电业局，长沙 410015）

变电站主变容量及台数的确定是电网规划和变电工程中主要的工作之一，关系到其所在的整个电力网络的安全、经济、可靠性。主变容量过大或者偏小都将给电力企业带来负面影响。如果主变装机容量过大，多台主变提前上马，就会出现“大马拉小车”的现象，造成资源浪费；如果主变容量过小，或者台数偏少，短时间内就面临负载率过高或者超载现象，变电站的可转供能力就下降，从电力系统供电可靠性考虑，必然扩容和更换，造成重复投资和建设。目前在编制电网规划或者建设变电工程项目确定主变容量和台数时，普遍是根据从业人员的设计经验结合规划区的负荷水平进行主观判断，缺乏一个系统化的决策流程和一组客观、合理的量化数据支撑。

近年来，随着国家节能减排政策的大力推行以及电力工业节能意识的提高，已经有不少电力系统专家及学者对变电站的经济容量方面做了相关研究。文献[1～3]从经济性与可靠性出发，从整体上对关系主变容量的电网规划进行决策优化；文献[4～7]单独把变电站作为一个孤立的研究对象，进行选址定容的优化研究；文献[8～9]以年费用为计算口径，按供电范围内单位容量所承担的年总费用最小为原则，对变电站经济容量和经济供电半径进行探讨，提出了相应的计算模型。这些模型短期内具有较好的实际效果，但没有考虑主变压器的维护费用以及更换或者退役时的回收费用，计算的年均费用没有考虑远景年的折现问题。

本文提出了一种基于全寿命周期成本管理的思想来确定主变容量及其台数的新方法。该方法着眼于变电站相关联的整个电力网络，以变电站全寿命周期费用LCC（life cycle costs）最小为原则，在保证可靠性的约束条件下构建一个计算模型，再用不可量化的约束条件对模型的计算结果进行优化，最终得到变电站的主变容量及台数。

1 方法概述

变电工程项目的全寿命周期成本LCC管理是站在全系统的高度，着眼于整个变电工程的生命周期，从项目立项、决策、设计、施工、运行维护、收尾等各阶段的全过程进行造价监控，从而使得变电站LCC最小[10～13]。主变的容量和台数直接决定了变电站的占地面积、总平面布置、出线回路数、主设备选择、开关的数量和费用，其确定方法是指在保证变电站所在的整个电力网络的供电可靠性的前提下，建立一个科学合理的数学模型，计算出变电站在整个经济运行年限内的LCC费用最小时的主变容量及台数。其中，LCC费用包括变电站以及与其关联的上下级网络建设的初始投资费用、运行维护费用、更换或者扩容的再次投资费用、报废回收费用等。基于LCC费用最小的主变容量及台数的决策过程的整体流程如图1所示。

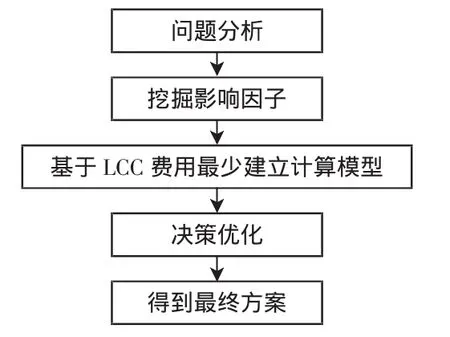
图1 容量及台数决策流程Fig.1 Flow chart of capacity and numbers decision

2 计算模型

2.1 基本的假设条件

本文所建立的模型，基于以下9个假设。

（1）变电站所在规划区内中压配电网覆盖面的电力负荷密度均匀。

（2）变电站的供电区域为圆形，变电站置于圆心位置，中压配电网为辐射网络结构。

（3）配电网主干线的导线截面按经济电流密度选择。

（4）变电站进线的平均长度与接线方式相关。

（5）以变电站全寿命周期单位变电容量成本最小为最终的目标函数，将扩建费用归算至变电站的运行维护费用中。

（6）在变电站全寿命周期内，规划区的负荷满足指数增长。

（7）考虑资金动态性（即需要费用折现）时，对变电站全寿命周期内的折现率统一取值。

（8）变电站LCC模型应该包括电气二次部分，但对于不同的主变容量方案所装配的二次设备差别不大，根据LCC模型中相同部分可以省略比较的原则，省略电气二次部分LCC分析。

（9）假设所有变电站为户外变电站，变电站寿命以其经济使用年限为20 a。

2.2 模型建立

从变电站所在的整个电网角度考虑，计算变电站LCC费用时考虑的关联网络如图2所示。

图2 系统关联网络Fig.2 Network of system correlation

2.2.1 初始投资的费用模型

由图2可知，新建一个变电站的初期投资费用包括变电站主体、高压侧进线、中压配电侧出线以及低压侧开关站的建设费用。其数学模型为

1）变电站主体的初期投资成本

整个变电站主体的初期投资建设费为

式中：a0为建设单台主变的投资中与变电站容量无关部分的系数，万元；b0为建设单台主变的投资中与变电站容量有关部分的系数，万元/MVA；S为单台主变容量；n为变电站初期投入的主变台数。

2）高压侧初期投资成本

变电站高压侧进线建设投资费用为

式中：al为与容量无关的单位长度进线总投资，万元/km；bl为与容量有关的单位长度、单位容量进线投资值，万元/（km·MVA）；L为N个变电站手拉手的平均长度，L的计算模型[14]为

3）中压配电侧初期投资成本

变电站中压出线建设投资费用为

式中：L′为中压配电网出线每回线路长度，L′=DR；M为中压配电网出线回路数，M=S cosφ/PAV，其中cosφ为线路上的平均功率因数，PAV为每回线路的平均负荷；AL为变电站配电网主干线导线总截面积，AL=S（/UNJ），其中J为导线的经济电流密度，UN为配电网额定电压；a2为反映中压出线投资中与导线截面积无关的部分的系数，元/km；b2为投资中与导线截面积成线性关系的系数，元（/km·mm2）。

4）低压侧初期投资成本

低压侧中压开关站的建设投资费用为

式中：FK为每个开关站的造价费用；NK为低压侧所需的开关站的个数，由文献[15]可知

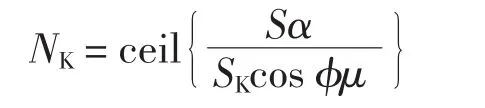
其中：SK为单个开闭所的总容量；α为区域负荷分配比例；μ为利用率。

2.2.2 运行与维护成本计算模型

1）变电站主体的运行与维护成本

变电站主体的运营成本由运行损耗费用和维护费用组成。其中的运行损耗费主要考虑变压器的电能损耗，即空载损耗和负载损耗。所以变电站的年电能损失费为

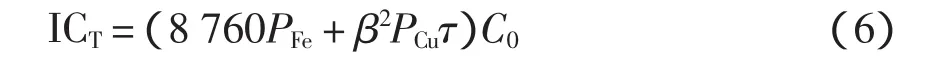
式中：PFe为单台变压器的空载损耗；PCu为单台变压器的短路损耗；β为变压器的负载率；τ为年平均最大负荷损耗小时数；C0为每度电的成本费用。

由于变压器的可用率很高，除了大修之外，每年的维护费用基本相同，可用典型的参数法进行估算，即

式中：θ为变电设备的可用率；b为设备的维护难度，即维护某种设备每小时所需费用。

变电站主体全寿命周期中发生的运行维护费用为

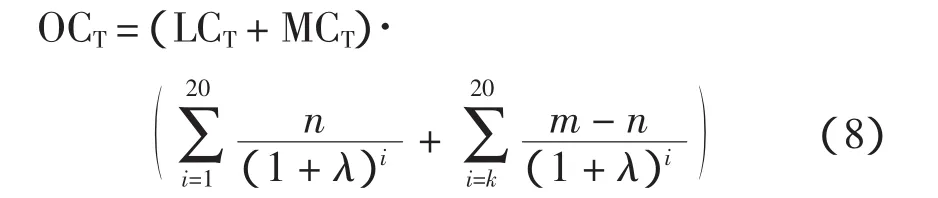
式中：m为终期主变台数；k为扩建年份；λ为折现率。

2）高压侧运行与维护成本

高压侧进线的运行和维护费用按照与初期总投资成正比例进行估算，即

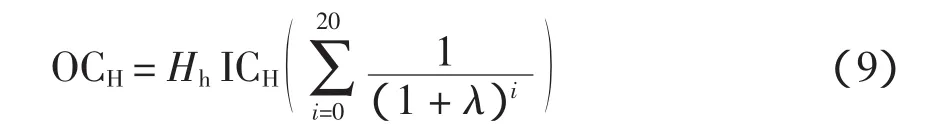
3）中压配电侧运行与维护成本

中压配电网络的运行和维护费用的计算可通过线损耗进行估算。不妨假设由等值线路代替变电站的中压出线，在最大负荷下，且与变电站的距离为l时，通过等值导线的电流为

因为d L=D d l，所以距离为d l的功率损耗为

配电网总的有功损耗为

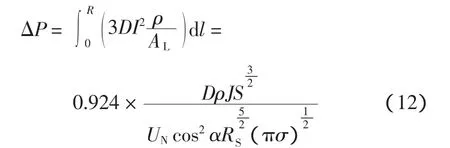
式中：ρ为导线电阻率；J为导线经济电流密度；σ为平均负荷密度；RS为容载比。

所以中压配电网的全周期线损费为

OCM=ΔPτC0=

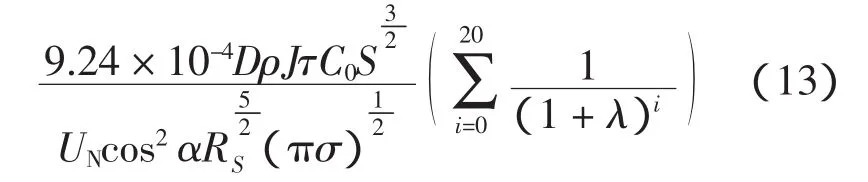
4）低压侧运行与维护成本

由于低压侧开关站的运行维护费用于变电站的容量关系不大，可按照与初期总投资成正比例进行估算，即

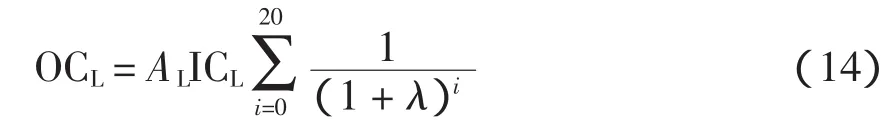
5）变电站增容扩建成本

通常新建一个变电站所支付的成本大约是对一个变电站进行扩容升级成本的2.3～3.5倍。因此，在变电容量跟不上负荷增长时，优先考虑对原有的变电站进行扩建，增加主变台数，以满足负荷需求，但终期主变台数不超过4台。其中，扩建年份的计算公式为

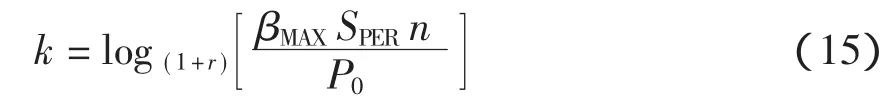
式中：SPER为单台主变压器的容量；r为变电站所在区域的平均负荷增长率；βMAX为按要求必须扩建的负载率的上限值。

在不新建变电站的情况下，当变电站的变电容量满足不了负荷需求时，就需要增加原有变电站的主变台数，对其进行扩容升级改造。相对于日常的运行维护费用而言，变电站的升级改造需要一笔较大的投资，所以在估算一个变电站的全寿命周期费用时，应该对扩容升级费用给以考虑。由以往的变电工程概算统计可知，折现之后，变电站扩建费用的数学模型为

式中：ω为扩容时增加1台主变的费用与初期投资1台主变的费用比值；ICPER为新建变电站时平均每台主变压器的投资费用；n′为扩建的次数；ki为第i次扩建的年份。

综上所述，整个变电站的运行维护费用为

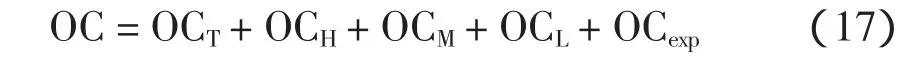
2.2.3 报废回收成本计算模型

由于变电设备含有大量的钢和铜，其退役之后的变压器和电线电缆仍然具有较高的残余回收价值，所以这部分价值也应该作为负值计算在全寿命周期成本之中，其数学模型为

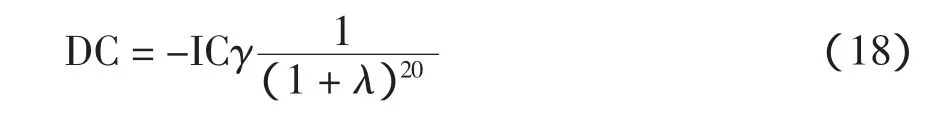
式中，γ为设备回收率，根据电力行业变电设备的特征，0～10 a内取35%，10～20 a内取27%。

2.2.4 目标函数

根据全寿命周期思想，以变电站全寿命周期内单位变电容量成本LCC最小为最终目标，选取费用折现值最小的方案为最优方案，即变电站主变容量及台数经济优化的目标函数为

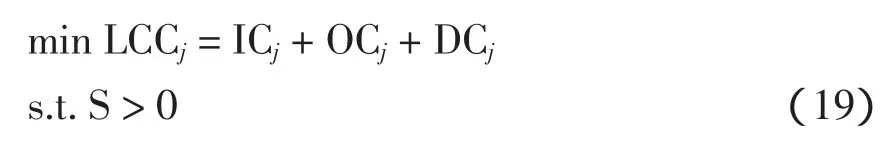
式中，LCCj为方案j的全寿命周期费用折现值。

3 算例

根据某省某地区配电网“十一五”发展规划，目前需要新建1个110 kV变电站，已知该站的进线220 kV变电站的变电容量配置为3×240 MVA。现取110/10 kV双绕组配电变压器为研究对象，根据文献[16～17]，结合当前国内电力市场现行电价以及配电网的一般情况，可设定一组基本参数：λ=0.1；P=2.1；D=1.3；R=1.376；H=6%；RS=2.0；PAV=4.5MW；UN=10 kv；μ=0.9；J=1.15 A/mm2；ρ=31.5Ω·mm2/km；τ=3 000 h；C0=0.5元/（kW·h）；SK=6 000MW；θ=99.5%；b=0.22万元/h；β=80%；ω=0.45。其余造价统计参数由设计院技经专业和高压建设部门提供的取值设定，如表1所示。

表1 变电工程费用参数表Tab.1 Parametersof substation engineering costs

3.1 选型方案比较

已知当前该地区的基础负荷为23MW，按当地的年平均负荷增长率计算，现阶段可供选择的主变容量及台数的配置方案如表2所示。

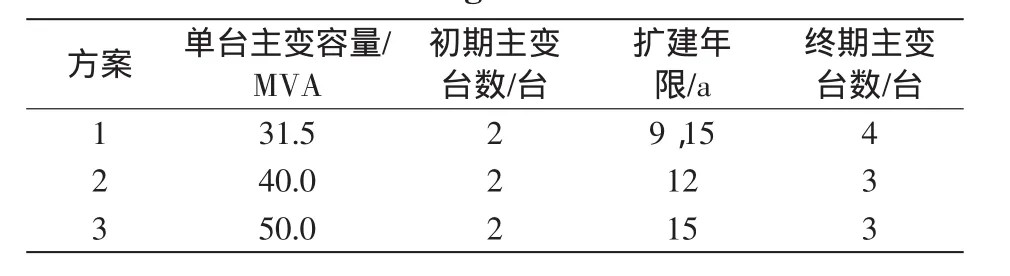
表2 各方案设置Tab.2 Setting of each schemes

由表2可知，方案1在变电站投运周期内需要扩容2次；方案2与方案3都只扩建1次，不同之处在于方案3初期主变容量较大，其扩建年份的时间比方案2晚。

将上述参数值代人式（19）中的模型计算，应用Matlab计算工具，可得到各方案的LCC费用，如表3所示。

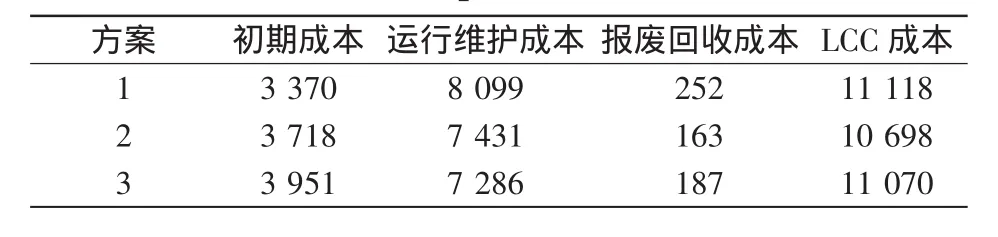
表3 各方案LCC比较Tab.3 LCC com parison of each scheme 万元

由表3可知，方案1由于初期配置的单台主变容量只有31.5MVA，导致变电站的全寿命周期内2次增容扩建，投资成本较大；方案3初期配置的单台主变容量为50.0MVA，初期台数为2台，在整个寿命周期内进行1次扩容，但与方案2相比，其提前上马的大容量主变增加了初期的投资费用，所以其综合费用比方案2略高。综上所述，方案2的全寿命周期成本LCC最低，因此该方案在给定的条件下最优。实际上，当前该地区实际的电网规划建设情况也确实是按本期2×40.0MVA、终期3×40.0MVA部署，结果与实际相符。

由上述算例结果可以看出，变电站LCC费用模型是立足于全周期的费用估算，综合考虑了建设初期的投入成本、投运之后的运行维护成本和退役之后的报废回收价值。建设初期投入费用的高低，并不能作为判别一个配置方案的优劣的标准，而只是作为一个最终评价值的组成部分，因为初期投入成本较低的方案可能后期的运行维护费用比其他方案高，例如方案1与方案2之间的关系。此外，由于变电站的运行维护费用占其总费用的比例最大，任何导致变电站更换主变、扩容升级改造的因素都会对变电站最终LCC费用造成影响。

3.2 负荷增长率影响分析

变电站供电区域的负荷增长率对该地区变电站规模配置影响很大，为了避免在较短年限内造成主变重载或者过载、转供能力和可靠性下降，导致重复建设和资源浪费。需要对主变容量的选择与负荷增长率之间的关系进行研究分析。

结合城市配网规划导则中主变台数不超过4台的原则，根据目标函数式（19）中的模型，代入第3.1节中的参数，设定不同的区域负荷增长率，可得不同额定容量的主变压器在不同的年平均负荷增长率下的最佳配置，如表4所示。

因为变电站实际的额定容量都是离散值，所以只有接近单台主变压器额定容量整数倍的配置方案才有意义。由表4可推得不同额定容量的主变压器在不同负荷增长率下的投运数量。表4是基于容载比RS为2.0的情况下得出的，而实际容载比为一个区间值，一般为1.8～2.3。因此在容载比允许的取值范围内，可以得出不同负荷增长率区间下的最佳主变容量配置规模，如表5所示。

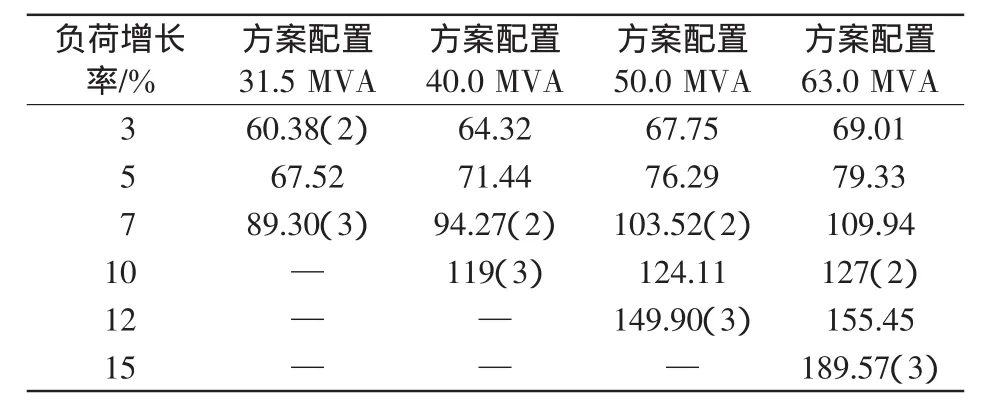
表4 不同负荷增长率下110 kV变电站的最佳容量配置Tab.4 Best capacity configuration of110 kV substations under different load grow th rate

表5 不同负荷增长率区间下的最佳主变容量配置规模Tab.5 Best capacity configuration of main transformer under different load grow th rate intervals

由表5可以看出，不同容量配置的变电站，在满足供电可靠性的前提下，通过计算所得的年平均负荷增长率是一个区间值，在这个负荷增长区间内变电站LCC才能取到最小值。

4 结论

（1）在配网规划决策中，变电站的主变容量及台数选择可采用LCC最小法进行分析与优化，以追求在全寿命周期内该变电站的综合成本最低。

（2）主变容量及台数的选择不能盲目追求初期投入成本的最低，而应该综合权衡初期投资成本、运营成本以及终期报废回收效益，使整个变电站LCC最低，这样决策将更加合理。

（3）应根据规划区的地域性质适当调整主变容量及台数。若是城区，则根据其中心城区的范围相对固定与否、各区域的功能和定位基本明确与否、其电网结构、电量需求饱和与否的实际情况，调整相应的主变容量及台数，使整个变电站在其寿命周期内成本最小。

（4）应加强各级电网长期规划研究，并不断滚动修编，为变电工程决策阶段采用LCC方法分析研究提供负荷预测、网架结构等基础数据。

[1]陈大宇，肖峻，王成山，等（Chen Dayu，Xiao Jun，Wang Chengshan，et al）.基于模糊层次分析法的城市电网规划决策综合评判（A FAHP-based MADM method in urban power system planning）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2003，15（4）：83-88.

[2]程浩忠，高赐威，马则良，等（Cheng Haozhong，Gao Ciwei，Ma Zeliang，et al）.多目标电网规划的分层最优化方法（The lexicographically stratified method for multiobject optimal electric power network planning）[J].中国电机工程学报（Proceedings of the CSEE），2003，23（10）：11-16.

[3]章文俊，程浩忠，程正敏，等（ZhangWenjun，Cheng Haozhong，Cheng Zhengmin，et al）.配电网优化规划研究综述（Review of distribution network optimal planning）[J].电力系统及其自动化学报（Proceedings of the CSUEPSA），2008，20（5）：16-23，55.

[4]李鑫滨，朱庆军（Li Xinbin，Zhu Qingjun）.变电站选址定容新模型及其遗传算法优化（New model optimized by genetic algorithm for distribution substation locating and sizing）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2009，21（3）：32-35，62.

[5]陶青松，肖峻，王笑一（TaoQingsong，Xiao Jun，Wang Xiaoyi）.基于地理信息的变电站选址定容模型与算法（Geographic information based substation locating and sizing model and algorithm）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2010，22（6）：32-37.

[6]刘自发，张建华（Liu Zifa，Zhang Jianhua）.基于改进多组织粒子群体优化算法的配电网络变电站选址定容（Optimal planning of substation locating and sizing based on refined multi-team PSO algorithm）[J].中国电机工程学报（Proceedings of the CSEE），2007，27（1）：105-111.

[7]杜茵，黄民翔（Du Yin，Huang Minxiang）.变电所投资风险决策模型及其应用（Risk decision model for substation investment projects and its application）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2006，18（4）：82-86，90.

[8]刘友强，李欣然（Liu Youqiang，LiXinran）.变电站经济容量和经济供电半径的探讨（Discussion on economical capacity and economical power supply radius for transformer substations）[J].广东电力（Guangdong Electric Power），2005，18（11）：7-9.

[9]Mikic O M.Mathematical dynamic model for long-term distribution system planning[J].IEEETrans on Power Systems，1986，1（1）：34-40.

[10]李涛，马薇，黄晓蓓（Li Tao，MaWei，Huang Xiaobei）．基于全寿命周期成本理论的变电设备管理（Power transformation equipment management based on life cycle cost theory）[J].电网技术（Power System Technology），2008，32（11）：50-53.

[11]丁坚勇，邓瑞鹏，李江（Ding Jianyong，Deng Ruipeng，Li Jiang）．发电设备的检修策略及可靠性管理研究（Research on overhaul strategy of generating equipments and its reliability management）[J]．电网技术（Power System Technology），2002，26（3）：72-75．

[12]黄向前（Huang Xiangqian）.浅谈变电所内变压器的经济运行（On economic operation of transformers in substations）[J].电网技术（Power System Technology），2000，24（3）：66-69.

[13]李泓泽，郎斌（LiHongze，Lang Bin）．全寿命周期造价管理在电力工程造价管理中的应用研究（The application of the whole life cycle engineering cost management on the electricity engineering field）[J]．华北电力大学学报：社会科学版（Journal of North China Electrical Power University：Social Science），2008，35（1）：7-11．

[14]胡丹，程浩忠，金华征，等（Hu Dan，Cheng Haozhong，Jin Huazheng，et al）.开发区配电网供电方式的选择方法（Selection method for power supply mode of distribution network in developing zone）[J].电力建设（Electric Power Construction），2006，27（8）：15-18.

[15]陈章潮，程浩忠．城市电网规划与改造[M]．2版.北京：中国电力出版社，2007．

[16]郭日彩，许子智，徐鑫乾（Guo Ricai，Xu Zizhi，Xu Xinqian）．220 kV和110 kV变电站典型设计研究与应用（Research and application of typical design for 220 kV and 110 kV substations）[J]．电网技术（Power System Technology），2007，31（6）：23-30，55.

[17]国家电网公司220 kV和110 kV变电站型设计协调组.220（110）KV变电站典型设计实施方案编制和推广应用手册[M].北京：中国电力音像电子出版社，2006.