运动靶标几何半径的确定方法

要俊杰, 姚志军, 潘高田, 张 昌, 黄一斌

(1. 装甲兵工程学院基础部， 北京 100072； 2. 63863部队， 吉林 白城 137001; 3. 装甲兵工程学院装备指挥与管理系， 北京 100072)

在导弹对空中目标的命中精度试验中，采用的是飞行的动态靶标。对每个不同空域仅打1发导弹的制导命中精度检验方案的设计问题，实际是复杂总体下检验方案的设计问题[1]。仅以命中次数和总的射击次数之比作为定数试验中的命中率是不够精确的，因为命中情况不仅与武器性能以及空域的高度、距离有关，也与目标的大小有关。目标尺寸越大，命中率就越高，因此描述武器命中精度应与武器各个方向[2]命中误差的分布有关。不同空域的命中误差分布是不同的，试验前给定对各个空域的命中精度要求，通常命中精度高的空域靶标半径应小一些，命中精度低的空域靶标半径应大一些。但实际中为了减少试验的复杂性，通常各空域会采用半径相同的圆柱形靶标。因此，如何设计适当的靶标半径，以体现武器的命中精度，以及在导弹未命中目标时，如何根据导弹与目标最近时刻的相对位置及空域特征对命中精度进行评判，解决基地和研制方关于检验结论的争议是本文研究的重点。

1 导弹命中概率计算的简化

在对目标进行打击时，导弹和目标同时在空中飞行，通过采集导弹和目标交汇前后的数据，分析击中目标情况。在弹体坐标系下，以导弹为坐标原点，将其视为静止，目标在相对运动，对测试数据进行相对坐标系变换时，需同时变换导弹命中误差服从的分布。变换后导弹命中误差服从正态分布，其径向误差均方差为σx，横向误差均方差分别为σy、σz。定量描述武器命中精度就是在弹体坐标系下，在目标所占空间区域内时命中误差的概率密度函数进行三重积分，求出的概率即为命中概率[3]。不同空域的命中误差分布的方差(与命中精度要求有关)不同。显然，这个命中概率既能反映导弹的命中精度，也能反映目标形状及体积，因此能更真实地反映导弹的命中精度。但由于命中概率的三重积分难以实现[3]，因此应将其合理转化为以二维正态分布进行二重积分来计算概率。

1.1 三维正态分布向二维正态分布的转化

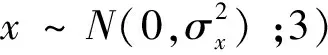
1.2 以弹着点为中心的坐标系变换

在导弹与目标距离较近时，测得导弹坐标点列和运动目标的坐标点列，选取导弹与目标距离最近的时刻进行相对坐标系变换，视导弹为静止，目标在相对运动，导弹中心点为相对坐标系的坐标原点oi，n个不同空域的目标中心相对于各个坐标原点的坐标为(xi,yi,zi)，i=1,2,…,n。这里(xi,yi,zi)是目标中心与弹道中心距离最近时刻的相对坐标。

定理1：在目标中心与导弹中心距离最近的时刻，导弹中心B与目标中心A一定在与直线弹道轨迹[6]垂直的平面上。

证明：如图1所示，在目标中心与导弹中心距离最近的时刻，设目标中心在A点，过A点垂直于弹道的平面为π，导弹轨迹距离目标最近的点为B，若B点不在平面π上，由直角三角形勾股玄定理可知B点不是距离A点最近的点，那么一定有另外一个点B′距离A最近，且B′在平面π上。

经过坐标系变换后，就可以只利用横向误差(yi,zi)来进行命中精度检验。

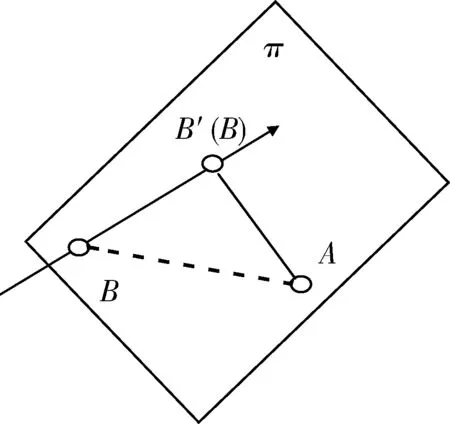
图1 目标中心与弹道轨迹位置关系

1.3 目标圆柱体在弹体坐标系的位置

为计算对目标的命中概率，应分析圆柱体目标在弹体坐标系中会以哪些形式出现。假定目标中心和导弹中心重合，图2、4、6为目标圆柱在弹体坐标系中的典型位置情况，图3、5、7为目标圆柱体在弹体坐标系oyz坐标面上的投影，即计算命中概率时进行二重积分的区域。

图2、4是目标圆柱体在弹体坐标系中的2种极限位置情况，图6是目标圆柱体在弹体坐标系中的一般位置情况。采用图6对目标命中概率进行计算的结果介于图2、4对目标命中概率进行计算的结果之间。由于正态分布经过正交变换后仍服从正态分布[1]，因此可通过正交变换将对命中概率的三重积分转化为二重积分。此时，图6的积分区域就可以转化为二维区域，即图3或图5的形式，只是σy和σz发生了变化[7]。

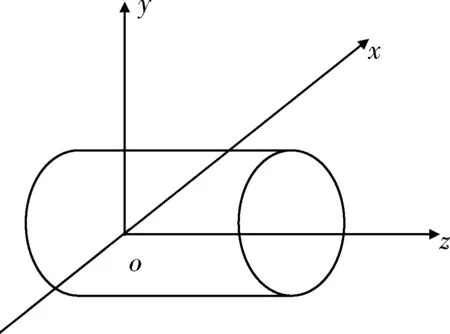
图2 目标圆柱轴与横向轴oz重合

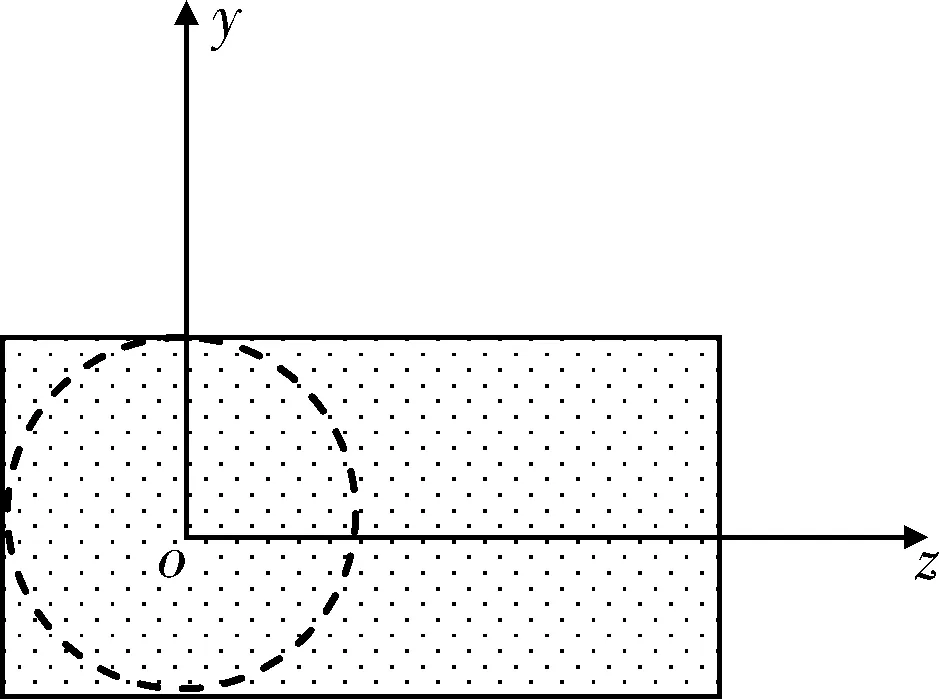
图3 投影区域为长方形

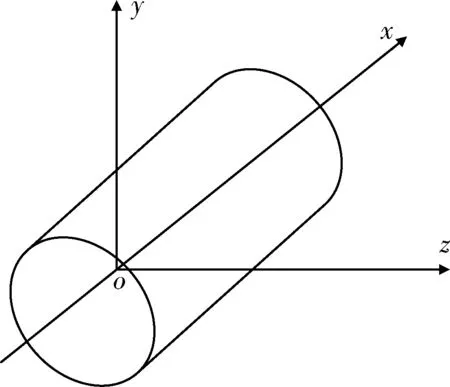
图4 目标圆柱轴与径向轴ox重合

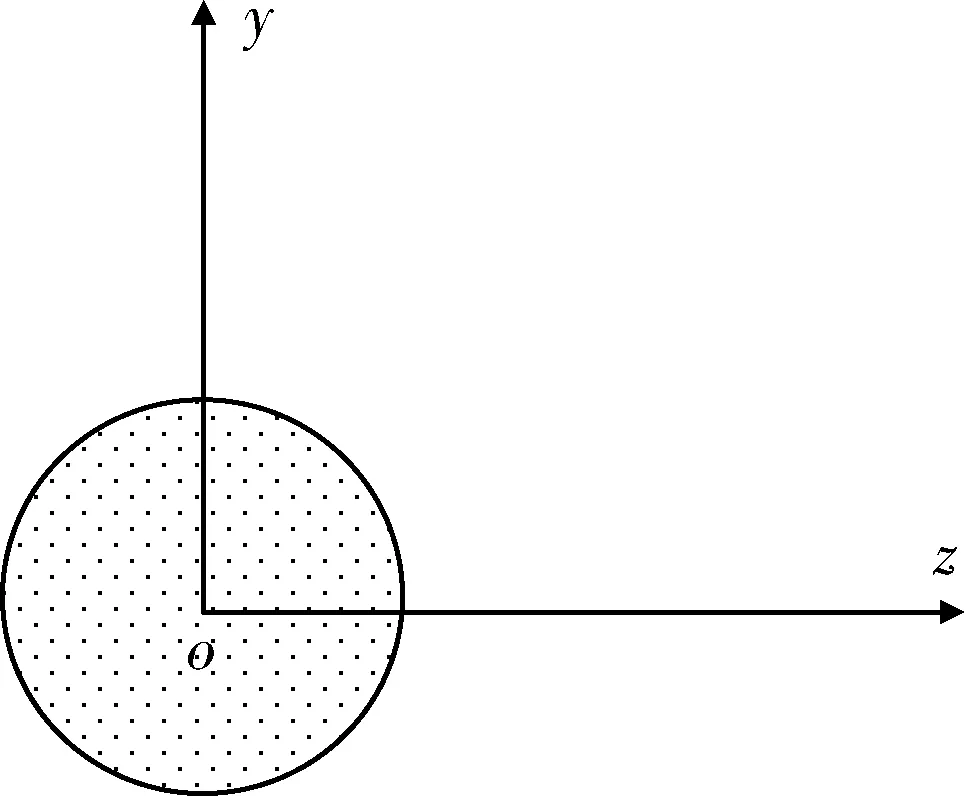
图5 投影区域为圆形

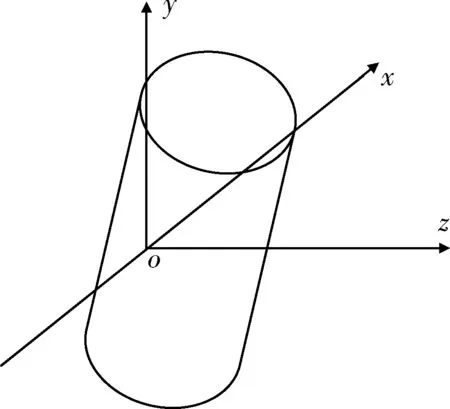
图6 目标圆柱轴与坐标轴均不重合

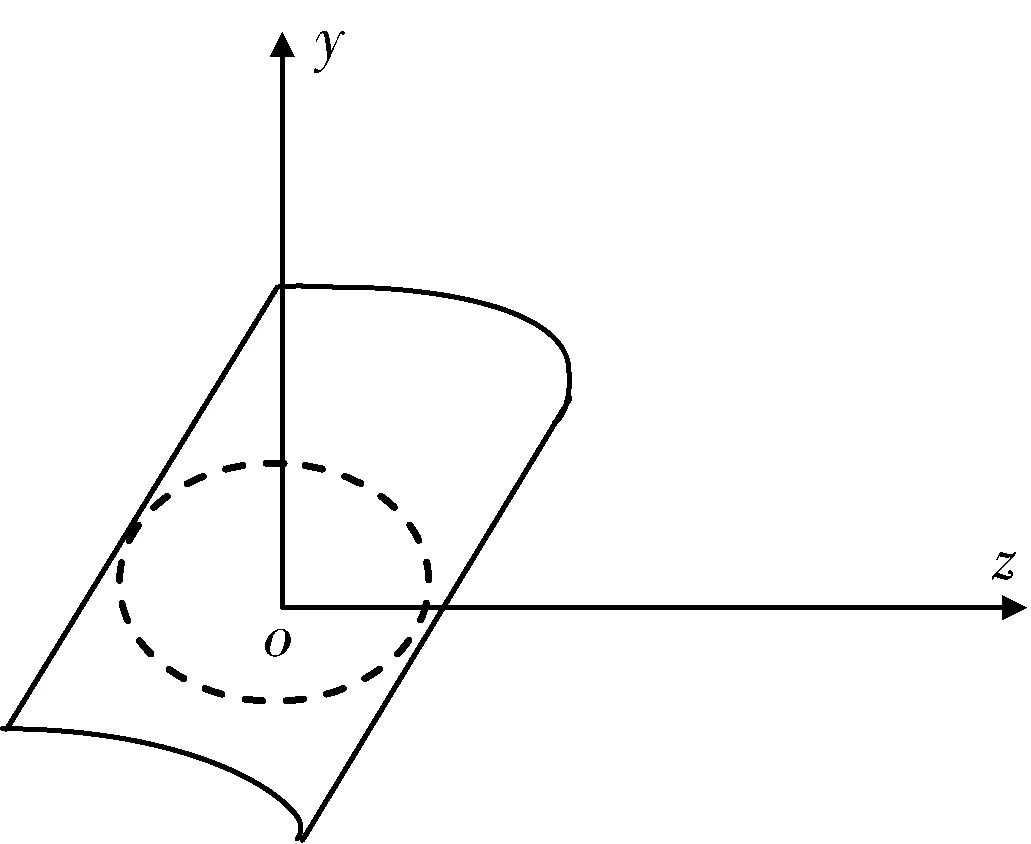
图7 投影区域为两边平行两边弧线

通过这种方法可以进行定型试验中防空导弹对一般空域的制导精度计算和落入概率评定。在图3、5、7中，以坐标原点为圆心，可以做一个圆(图中用虚线表示，图5中与投影圆重合)。这个圆的半径就是靶标的半径，对目标的命中精度问题就是对这个圆的命中概率问题，而计算这个概率与导弹的横向偏差σy、σz有极大关系。

2 检验方案的设计

在试验时，会出现这样的情况:虽然导弹没有击中目标，但分析实际测试数据后发现导弹飞过目标的瞬间彼此间距离非常近。此时,由于采用固定尺寸靶标，基地和研制方参试人员对这种情况就很容易产生争议，难以说清是否算作击中。因此，希望设计一个临界值L，当靶标和导弹接近的最短距离≤L时，算作击中；否则算作没击中。

2.1 命中误差分布的方差检验效率函数

通过坐标变换得到坐标yi～N(0,σyi0),zi～N(0,σzi0),i=1,2,…,n，对命中精度的检验就是对不同空域的复合总体的横向偏差(σyi0,σzi0)进行检验。类似于文献[3]的讨论,笔者只考虑7发1不中检验问题的效率函数，首先提出检验的假设问题。

H0:σi≤σi0。

H1:σi≥σi1。

对于每个空域目标相对弹着点中心的偏差坐标(yi,zi)，有

(1)

由于各空域的独立性，所有yi和zi(i=1,2,…,7)间均相互独立。

(2)

这里

β(σ)=β(σy1,σy2,…,σy7;σz1,σz2,…,σz7),

β(σ0)=β(σy10,σy20,…,σy70;σz10,σz20,…,σz70),

β(σ1)=β(σy11,σy21,…,σy71;σz11,σz21,…,σz71)。

第i发导弹的命中概率[9]为

(3)

未命中目标的概率为

(4)

在检验过程中，当H0成立时，β(σ0)为导弹精度达到要求(产品为合格事件)的概率。

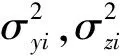
定理2:对于概率函数β(σ)变量的任一分量σyi或σzi，当只有一个σyi→∞(σzi→∞)时，β(σ)是σyi(σzi)的单调减函数；当7组变量中至少有2组的变量σyi→∞,且σyj→∞(σzj→∞),i≠j时，β(σ)单调减且趋于0。

由于k→∞，则此式必趋向于0。考虑第2项中

由于k→∞，则此式也必趋向于0。

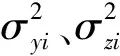
由鉴别比k与σi的关系可知：当k增大时，σi增大，从而β(σ)也是k的单调减函数。因此β(σ)可作为检验问题的效率函数[8]。

2.2 检验方法

为了研究检验方案的拒真风险α和纳伪风险β，考虑求解下列问题。

H0:σyi=σyi0;σzi=σzi0。

H1:σyi=σyi1;σzi=σzi1。

β(σ0)≥1-α，

(5)

β(σ1)≤β，

(6)

σ1=kσ0。

当H0成立时，式(5)变为

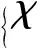
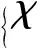
(7)

当H1成立时,式(6)变为

(8)

求解非线性不等式(7)、(8)，可以得到a和k。

2.3 检验的临界值

采用搜索求根的方法，对于n(n=4,5,6,7,8)发1不中试验,计算试验方案真实的拒真风险α′、纳伪风险β′及临界值参数，如表1-5所示。

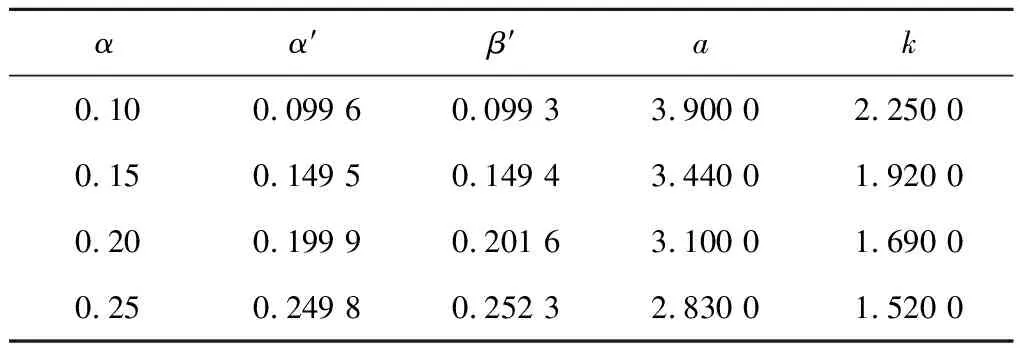
表1 4发1不中

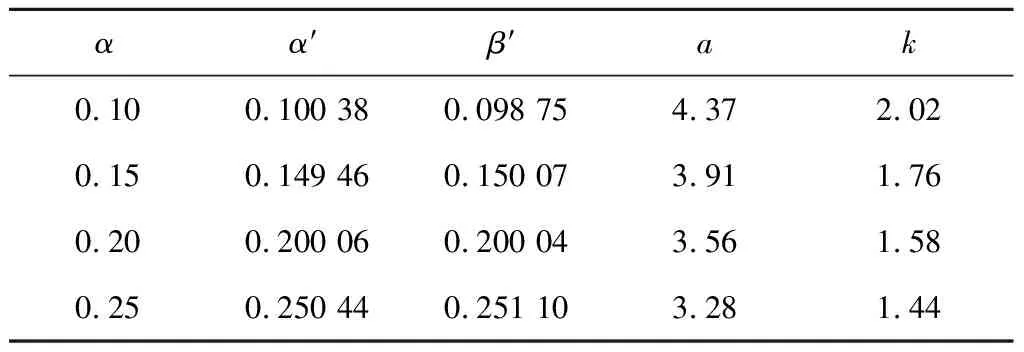
表2 5发1不中

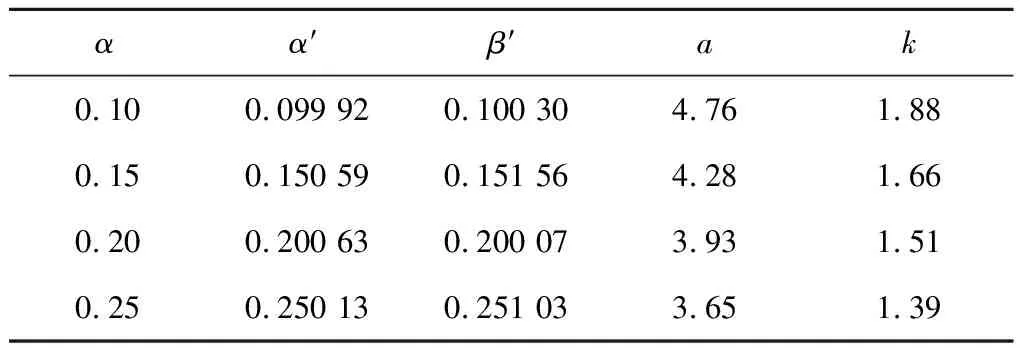
表3 6发1不中

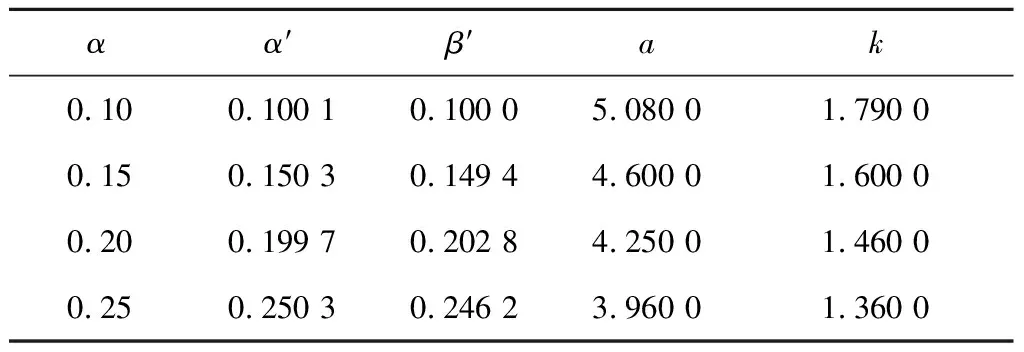
表4 7发1不中

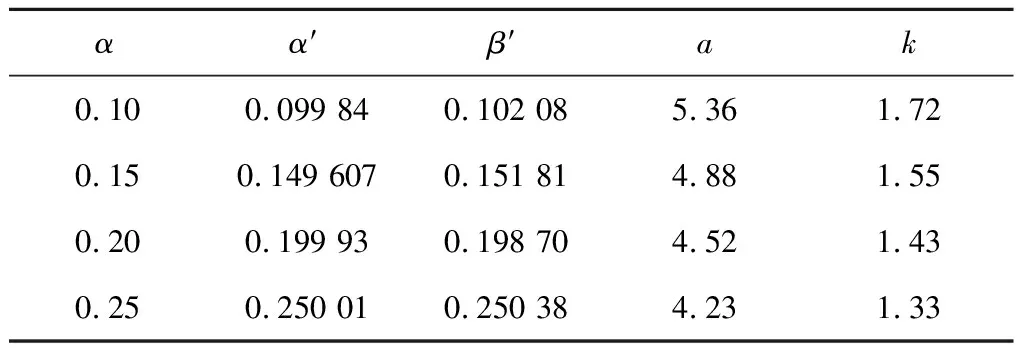
表5 8发1不中

3 靶标半径的确定

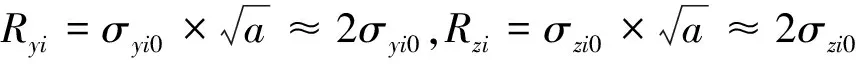
为使试验操作简单易行，可以把目标圆柱的半径设置为

(9)

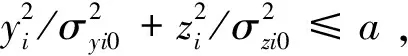
4 结论

本文具体给出了导弹命中精度检验中靶标半径的确定方法，同时给出了对检验过程中测试数据科学评定的理论依据和方法，为基地命中精度试验的定量定性分析提供了依据，对导弹命中精度的检验问题具有重要意义。研究结果还有助于设计使用检验功效高、2类风险小的定型试验方案。

参考文献：

[1] 闫章更,濮晓龙.现代军事抽样检验方法及应用[M].北京:国防工业出版社,2008:48-51.

[2] 李新国,方群.有翼导弹飞行动力学[M].西安:西北工业大学出版社, 2005:30.

[3] 杨雷,潘高田,王勇杰.小样本三维正态分布整体检验射击精度方法研究[J].装甲兵工程学院学报,2005, 19(1): 26-28.

[4] 汪荣鑫.数理统计[M].西安:西安交通大学出版社,1986:176-192.

[5] 张尧庭,方开泰.多元统计分析引论[M].北京:科学出版社,1997:66.

[6] 潘高田,梁帆,张昌.基于单发地空导弹测试数据的武器精度检验[J].装甲兵工程学院学报, 2011, 25(6): 50-52,92.

[7] 北京大学数学力学系几何与代数教研室代数小组.高等代数[M].北京:北京大学出版社,1978:240-243.

[8] 陈家鼎,郑忠国.概率统计[M].北京:北京大学出版社,2007:339.

[9] 王勇杰,潘高田,杨雷.二维正态分布不同方差小样本检验射击精度方法研究[J].装甲兵工程学院学报,2004, 18(4):19-21.