X射线脉冲星导航的相对论定位法初探

孙维瑾， 费保俊

(装甲兵工程学院基础部，北京 100072)

无论是卫星导航，还是现在正在研究中的X射线脉冲星导航(X-ray pulsar-based NAVigation, XNAV)，都是测量光波从导航星座(卫星或脉冲星)到达观测者的传播时间，即光子到达时间(Time Of Arrive,TOA)。由于光速不变性，TOA等价于导航星座到观测者的距离, 姑且将这种导航方法称作TOA定位法。从纯粹广义相对论的观点来看，TOA定位法中测量的系统时间(如BDT或GPST)属于坐标时间。在考虑引力作用的情况下，坐标时间并不满足光速不变性，于是将引力对测量时间的影响(相对论效应)作为一种修正加进去，因此TOA定位法实际上是一种半经典理论，是经典力学与相对论的混合体。

原则上说，直接在相对论框架内建立导航理论是完全可行的，有不少学者在这方面作了深入探讨。2002年，Rovelli[1]在深入研究卫星导航理论过程中，首先将相对论测量理论引入导航系统，提出GPS中的可观测量是指固有量而并非坐标量，认为应该借鉴相对论天体物理的研究方法，在4维零标架中讨论光传播问题，因为零标架的一个明显特性是与坐标变换无关；Blagojevic等[2]随后建立了一种共轭零标架，将对应坐标称为GPS典型坐标；Coll等[3-5]将这一方法系统化，提出4个发射体的固有时间构成4维时空的光坐标或发射坐标，可以为任意观测者定位导航；文献[6-8]进一步完善了这一理论。由此建立起来的理论体系称之为相对论定位系统(Relativistic Positioning System, RPS)，它是以相对论测量理论为基础的一种全新的导航方法。

RPS相对于TOA定位法有一个明显的优点，就是测量的不是坐标时间而是发射体的固有时间，在脉冲星导航等深空导航领域得到实际应用是有可能的，这里就此作一些探讨。

1 相对论定位系统基本原理

〈xa,xa〉-2〈xa,x〉+〈x,x〉。

(1)

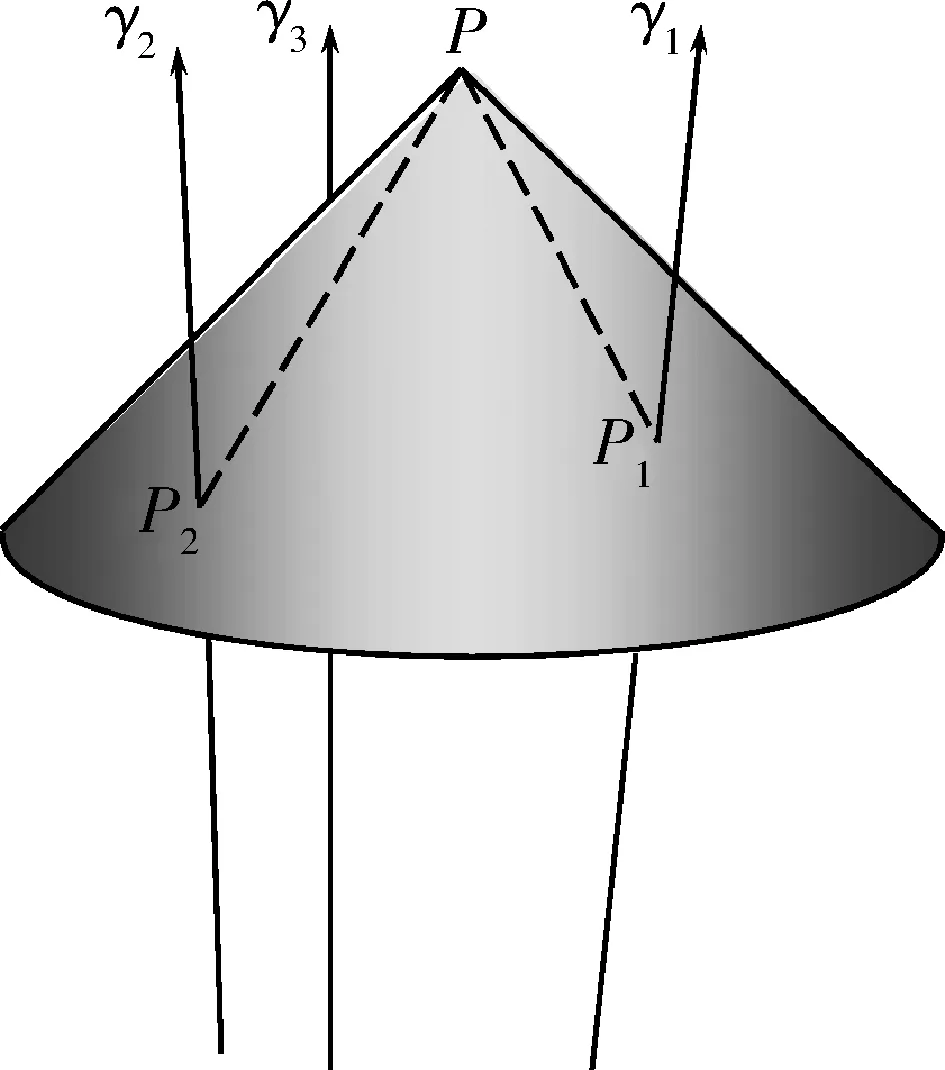
图1 发射体的世界线与观测者的过去光锥

以下取c=1的自然单位制。假设发射体的3维速度va为常量，则4维闵氏速度也是常量，即

(2)

积分得

(3)

(4)

时空间隔变为

(τa)2-2τa〈ua,(x-xa(0))〉+〈(x-xa(0)),(x-xa(0))〉=0。

(5)

令观测者4维位置矢量与发射体初始位置矢量的差值为

za(x)=x-xa(0)，

(6)

则有

(τa)2-2τa〈ua,za〉+〈za,za〉=0。

(7)

由此解出

(8)

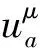
式(8)表明发射体的固有时间是观测者坐标的函数，即

τa=τa(zμ)，a=1,2,3,4。

进一步将其视为一种坐标变换，只要变换矩阵的行列式不为0，则

zμ=zμ(τa)，μ=0,1,2,3。

即观测者坐标也唯一地由τa所确定。因此可以将4个发射体的固有时间(τa|a=1,2,3,4)当成观测者坐标，称之为光坐标(light coordinates)或发射坐标(emission coordinates)。

既然光坐标构成坐标系，就应该有相应的标架和度规。对式(8)求微分，可得到

(9)

(10)

不难求出度规张量的对角元素

(11)

因此光坐标{τa}构成零标架。

2 脉冲星导航的相对论定位法

上面的讨论是假设发射体的3维速度va为常量，由此可见：应用RPS的前提条件是导航星座应该具有常速度，而X射线脉冲星正好具备这一条件，它在太阳系质心参考系(Bary Centric Reference System, BCRS)中的速度(自行)具有确定值(在短时间内甚至可以视为静止)。以BCRS为基准对XNAV的相对论定位法进行探讨，以下在2维时空得到的结论可以很方便地推广到4维时空。

在BCRS中引入2维Newman-Penrose标架{ω1,ω2}及其坐标{X1,X2}={U,V}，与2维正交标架{e0,e1}及其坐标{t,x}的关系分别为

(12)

(13)

根据式(12)和(13)，可知新标架下的度规和线元分别是

(14)

dτ2=gabdXadXb=2dUdV。

(15)

由于度规的对角分量g11=g22=0，故{ω1,ω2}是零标架。

设脉冲星a(a=1,2)在BCRS中的速度va=const，根据式(2)和(13)，可知脉冲星的闵氏速度矢量在零标架下的分量也为常量，即

(16)

式中：

是va对应的闵氏时空双曲角[9]。设脉冲星的初始坐标分别为(Ua(0),Va(0))，对式(16)进行积分，得到它们的坐标为

(17)

根据发射点(Ua,Va)与接收点(U,V)的时空间隔

2(U-Ua)(V-Va)=0，

(18)

解出U=Ua或V=Va。如果航天器位于2颗脉冲星之间，则接收点的坐标为

(19)

式(19)也可以根据式(8)求出。将

代入式(8)，求出脉冲星a的固有时，即

τa=γa[(Δta-vaΔxa)-|vaΔta-Δxa|]，

(20)

于是得到

(21)

在式(21)中分别取a=1,2，就得到式(19)。

2维时空的相对论定位法如图2所示，下面通过图2作具体说明。

图2中：{t,x}和{U,V}分别为正交标架和零标架；γ、γ1、γ2分别为航天器和2颗脉冲星的世界线。由于脉冲星做匀速运动，脉冲星世界线是2维时空的斜直线，与时间轴的夹角θ=arctanv(取c=1)反映了脉冲星在BCRS中的速度，图中显示的是

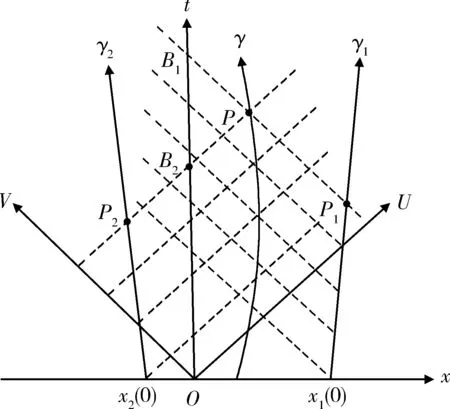
图2 2维时空的相对论定位法

脉冲星1和2分别沿x轴正向和负向运动。设初始时刻t=0时，τ1=τ2=0，2颗脉冲星的空间坐标分别为x1(0)和x2(0)，则变换到零标架为

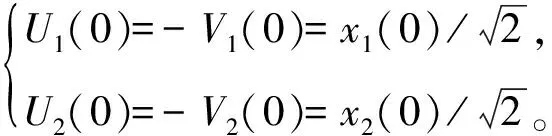
脉冲星不断沿自身的光锥发射光波，这些波矢量构成坐标系{U,V}的坐标网格(grid)，每一条波矢量就是一条坐标线，对应于一颗脉冲星的固有时间。例如：设2颗脉冲星的固有周期分别是T1、T2，它们每隔一个周期发射一个脉冲，则图中过P1、P2点的波矢量对应的固有时分别为τ1=5.0T1，τ2=4.0T2。如果航天器位于这2条波矢量的交点，则它对应的光坐标就是(τ1,τ2)。

3 RPS定位法与TOA定位法的比较

利用坐标变换式(13), 将式(19)变换到通常的正交系{t,x}，则有

(22)

在2颗脉冲星的速度(v1,v2)和初始位置(x1(0),x2(0))已知的情况下，航天器的时空坐标(t,x)由光坐标(τ1,τ2)来确定，这是相对论定位方法。

(23)

(24)

与式(22)比较，航天器的时空坐标可表示为

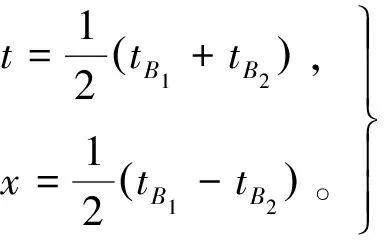
(25)

如果航天器携带高精度原子钟可以确定光子到达航天器的时间t，则只需测量一颗脉冲星的光子到达SSB的时间tB1或tB2，即可确定航天器的位置，即

x=tB1-t=t-tB2。

(26)

这就是不考虑引力作用情况下的TOA定位方法。

由于式(25)和(26)可从式(22)导出，因此在理论上RPS与TOA定位法是统一的；但由于测量对象不同，其在实践中是有区别的。

TOA定位法需要已知tB，它们是指航天器接收到光脉冲的同时假想SSB接收同一脉冲的坐标时间。在实际测量中，设航天器在某一时刻测得特定脉冲星观测轮廓的相位是φ(t)，因为SSB接收的脉冲星标准轮廓的固有频率fP和初始相位φ(0)是已知量，根据Taylor级数展开式可以推算出SSB的标准轮廓在任意时刻的相位，当相位与φ(t)相同时的时间即为tB，由下式确定[10-11]：

(27)

式中：fP(k)为频率的k阶时间导数。由此可见：光子到达SSB的时间并非直接测量值，而是由某一参考时刻的标准轮廓推算出来的。

在RPS中，tB只是中间变量(或者根本不需要)。由式(24)可知：它们可由脉冲星的固有时及其初始位置来确定。而脉冲星的固有时乃是直接测量值，可以根据航天器接收的脉冲星观测轮廓的相位φ(t)(包含整波数)以及脉冲星固有周期TP直接得到，即

τ(t)=φ(t)·TP，φ(0)=0。

(28)

这就是RPS的优越性。

4 结论

1) 相对于TOA定位法，RPS使得时间测量较为简单可靠，它只需测量观测轮廓的相位，实际上就是计算对应于脉冲星固有时的波数，不必以标准轮廓的周期为标准进行转换，并与标准轮廓进行比较。

2) 因为RPS测量的不是坐标时间，在工程上不必建立严格的时间系统，但仍需建立空间系统，如太阳系质心系或地心系的空间坐标系。

3) 在TOA定位法中，脉冲星的方向数据必须精确，而脉冲星的速度和初始距离对导航的影响不大。但采用RPS必须精确给出这2种参量，而天文观测数据难以达到导航所需的精度，这可以通过实验的方法来解决：如果精确测量2组数据(t,x,τ1,τ2)，根据式(22)可得到4个方程，由此即可解出2个脉冲星的速度和初始位置(v1,v2,x1(0),x2(0))。

以上讨论没有涉及引力场的影响，下一步将对此进行研究。

参考文献：

[1] Rovelli C. GPS Observables in General Relativity[J]. Phys Rev D, 2002, 65(4):044017.

[2] Blagojevic M, Garecki J, Hehl F W ,et al. Real Null Coframes in General Relativity and GPS Type Coordinates[J]．Phys Rev D, 2002,65(4):044018.

[3] Coll B, Ferrando J, Morales J. Two-dimensional Approach to Relativistic Positioning Systems[J]. Phys Rev D,2006, 73(8)：084017.

[4] Coll B, Ferrando J, Morales J. Positioning with Stationary Emitters in a Two Dimensional Space-time[J]. Phys Rev D, 2006, 74(10):104003.

[5] Coll B, Pozo J. Relativistic Positioning Systems: the Emission Coordinates[J]. Class Quantum Grav, 2006,23(7): 7395-7416.

[6] Ruggiero M L, Tartaglia A. Mapping Cartesian Coordinates into Emission Coordinates: Some Toy Models[J]. Int J Mod Phys D, 2008,17(2):311-326.

[7] Bini D, Geralico A, Ruggiero M L，et al. Emission Versus Fermi Coordinates: Applications to Relativistic Positioning Systems[J]. Class Quantum Grav, 2008,25(20):205011.

[8] Bunandar D, Caveny S A , Matzner R A. Measuring Emission Coordinates in a Pulsar-based Relativistic Positioning System [J]. Phys Rev D, 2011, 84(10):104005.

[9] 费保俊. 相对论与非欧几何[M]. 北京：科学出版社，2005:77.

[10] 杨廷高，南仁东，金乘进，等．脉冲星在空间飞行器定位中的应用[J]. 天文学进展，2007, 25(3): 249-261.

[11] 费保俊，姚国政，杜健，等．X射线脉冲星自主导航的脉冲轮廓和联合观测方程[J]．中国科学: 物理学力学天文学，2010，40(5): 644-650.