Fe基热喷涂涂层切削加工表面质量研究*
③
(①装甲兵工程学院装备维修与再制造工程系,北京 100072;②装甲兵工程学院 装备再制造技术国防科技重点实验室,北京 100072;③北京理工大学机械与车辆学院,北京 100081)
损伤零件再制造技术已经在航空发动机、重型机械以及汽车关键零部件修复中得到了广泛应用[1]。热喷涂是再制造领域中的关键技术,零件热喷涂之后在尺寸精度、表面质量等方面一般不能达到使用要求,因此对其进行一定的机械加工是非常必要的。热喷涂涂层因其独特的成形特点,与一般均质材料的机械加工具有一定的差异。本文依托再制造技术国防科技重点实验室制备的FeAlCrBSiNb涂层,采用正交试验法,对其切削加工表面粗糙度和结合强度进行研究,旨在探索Fe基非晶涂层切削加工的特点及一般规律,为再制造技术的推广做出贡献。
1 试验条件及设备
利用电弧喷涂技术制备FeAlCrPSiNb涂层,采用的喷涂工艺为:喷涂电压36 V,电流150 A,空气压力0.7 MPa,喷涂距离200 mm,转台速度700 r/min,基体材料45钢,喷涂厚度1 mm。
采用再制造技术国防科技重点实验室研制的车铣复合机床进行切削加工,刀具选用硬质合金刀具。加工工件直径为45 mm,长度为100 mm。
采用时代TA620型表面粗糙度仪对加工后的工件表面粗糙度进行测量。
采用微机控制电子万能试验机SANS Power Test对涂层加工后的结合强度进行测试。
2 正交试验设计
2.1 试验参数选择
Fe基涂层材料特性与均质材料存在以下差异:(1)涂层内部由金属粒子相互搭接而成,存在非均质颗粒和孔隙,在加工过程中易发生冲击现象,影响切削加工后涂层的表面质量。(2)涂层与基体结合方式为机械结合和物理结合[2],加工过程中不合理的切削用量易导致涂层脱落。(3)非晶涂层由于其喷涂工艺限制,通常厚度较小,因此切削深度一般小于均质材料。
依据FeAlCrPSiNb涂层的性能及现有的研究成果[3-4],参考切削加工手册中的的经验数据[5],对切削深度、切削进给量、切削速度进行设计。
采用3因素3水平正交试验对Fe基涂层进行切削加工。所选因素水平如表1所示。
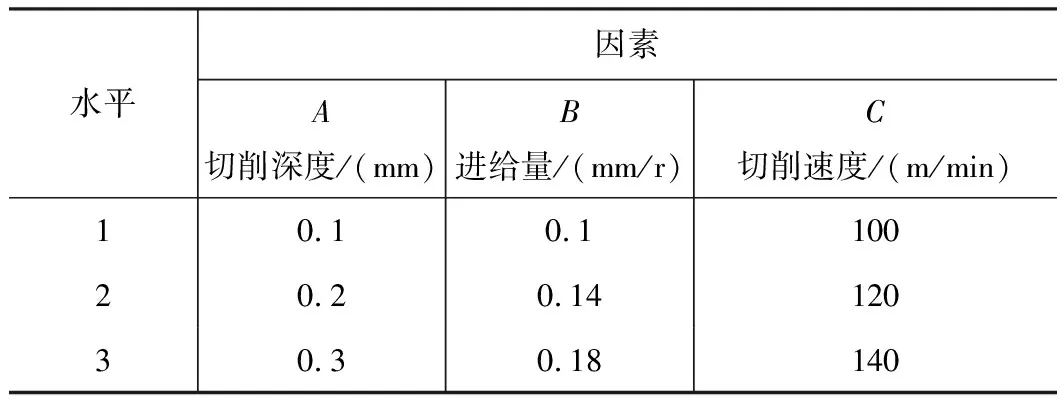
表1 正交试验因素和水平
2.2 切削试验方案设计
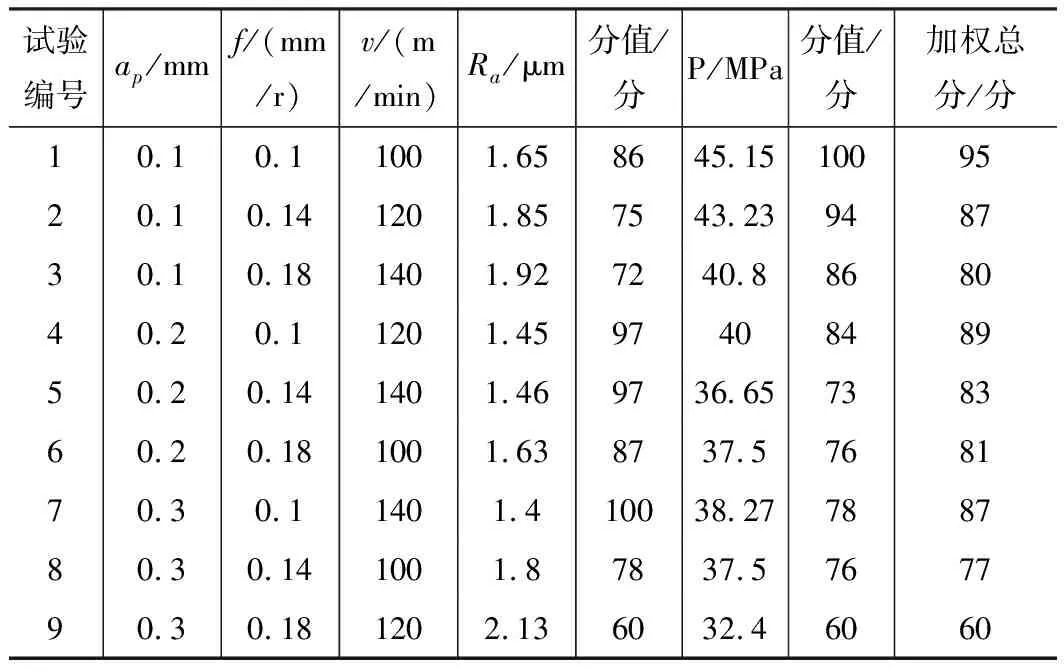
采用L9(34)标准正交表进行试验方案的设计,如表2所示,共需进行9次试验。采用正交试验方案中的切削用量组合进行试验,每次试验加工长度为10 mm。图1为加工后的工件。

3 测量及工艺优化
3.1 表面粗糙度测量及分析
对工件各加工段的表面粗糙度进行测量(如图2所示),每段测量5次,取5次的平均值,如表2所示。通过表中数据可以看出,采用本文所设计的正交试验加工参数可以得到较高的表面质量,表明Fe基非晶涂层具有良好的加工性能。

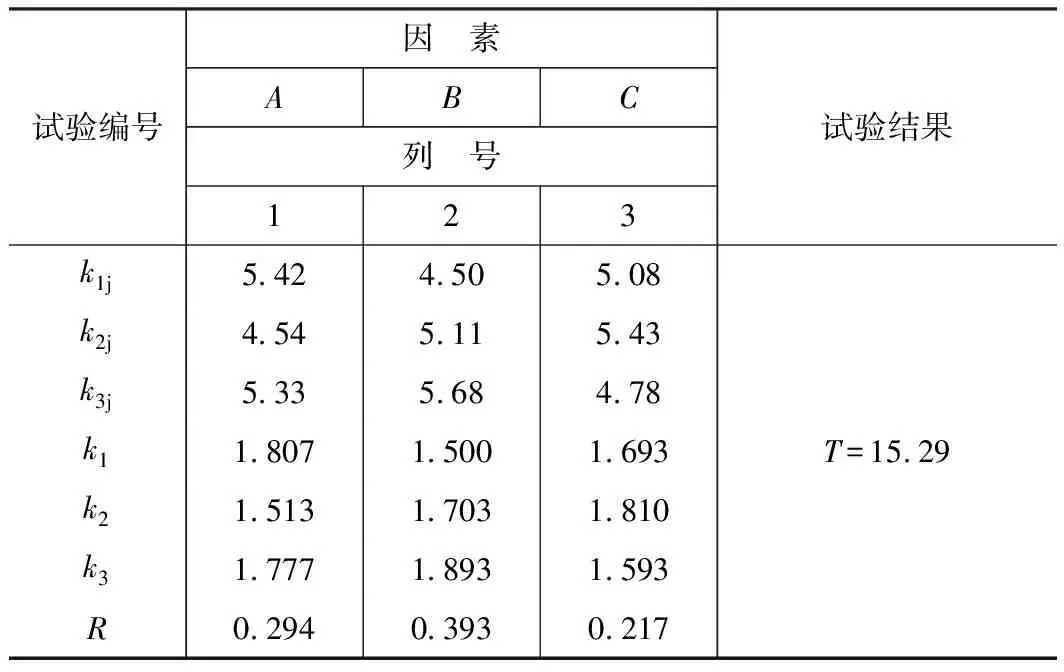
表3为表面粗糙度极差分析结果,从中可以看出,极差R的大小顺序为:RB>RA>RC,表明Fe基非晶涂层切削加工参数对加工表面粗糙度的影响大小顺序为:进给量>切削深度>切削速度。
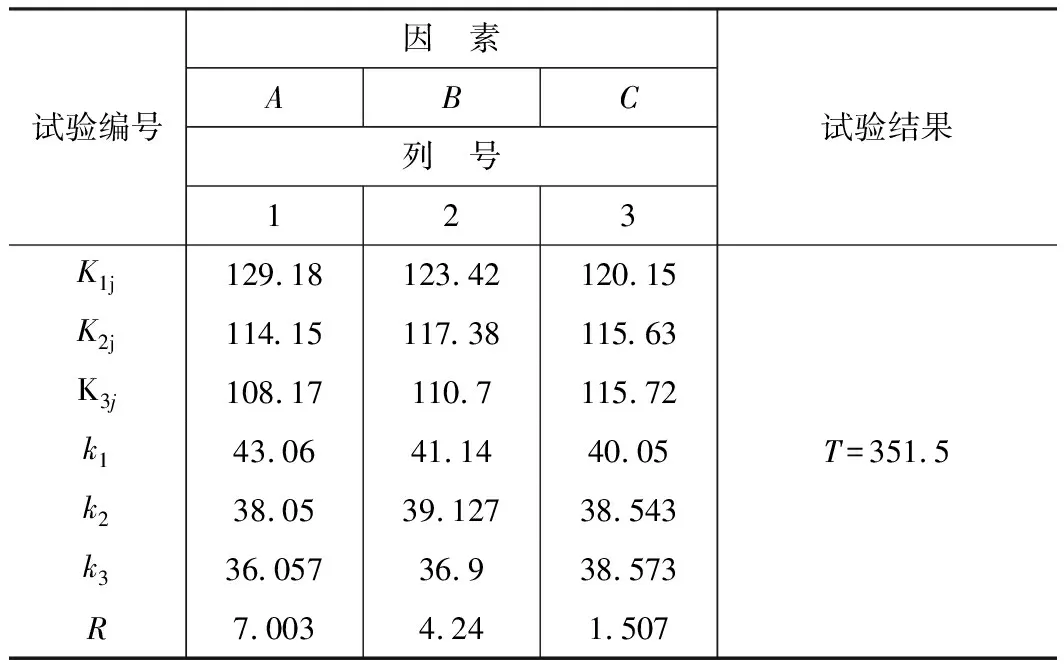
由各因素的均值ki可以看出在A列:k2 表4为表面粗糙度方差分析结果,从中可以看出3<6.5 表2 正交试验方案及结果 表3 表面粗糙度极差分析结果 表4 表面粗糙度方差分析结果 因此,在Fe基非晶涂层切削加工中,为得到更好的表面质量,提高工艺优化的效率,对工艺参数进行优化时应优先考虑切削进给量,其次考虑切削深度和切削速度。 3.2.1 涂层结合强度测量及结果分析 参考回转体结合强度研究[6]中的测量方法对切削加工后的涂层结合强度进行测量,试验现场如图3所示。 以涂层完全脱落时所测数据为有效数据。图4为涂层完全脱落后的试样。表2中P为9组实验所测结合强度,表5为其极差分析结果。 从表5可以看出,极差R的大小顺序为:RA>RB>RC,表明Fe基非晶涂层切削加工中影响涂层结合强度的因素影响大小顺序为:切削深度>进给量>切削速度。 由各因素的均值ki可以看出在A列:k1>k2>k3;B列:k1>k2>k3;C列:k1>k3>k2,因此最优方案为A1B1C1,即切削深度为0.1 mm,切削进给量为0.1 mm/r,切削速度为100 m/min为试验所得最优加工方案。 表5 涂层结合强度极差分析结果 表6 结合强度方差分析结果 由表6可以看出0.99<6.02 3.2.2 涂层结合强度预测模型建立 为探究切削参数与涂层加工后结合强度的数学关系,利用统计回归法,采用指数函数建立结合强度与切削参数之间的预测模型,如式(1)所示: (1) 其中:P是结合强度;c为常数;x,y,z分别为各切削参数的指数。对上述公式两边分别取自然对数可得: lnP=lnc+xlnap+ylnf+zlnv (2) 令Y=lnP、a=lnc、X1=lnap、X2=lnf、X3=lnv,式(2)可变形为: Y=a+xX1+yX2+zX3 (3) 式中:a为常数项,x、y、z为lnσ对Xi(i=1、2、3)的偏回归系数。将表2中的测量数据P代入式(3)可得如下方程组: (4) 根据最小二乘法原理,令多元线性回归方程的残差平方和最小,求得a和x、y、z。该预测模型计算结果如式(5)所示。 (5) 对该模型进行假设检验,其显著性水平P值为0.003 13,远远小于参考量0.01,说明模型高度显著。为验证该模型的准确性,将试验中的切削参数代入公式(5)中,求出在本文中切削参数加工条件下的结合强度预测值,如表7所示。从表7中可以看出,切削速度在100~140 m/min,切削进给量在0.1~0.18 mm/r,切削深度在0.1~0.3 mm条件下,通过预测模型计算得到的预测值与试验实测值误差在5%以内,充分验证了该模型的准确性。 表7 结合加工后结合强度实测值与预测值对比 注:误差=(预测值-测量值)/测量值 利用Matlab分别绘制切削深度0.1 mm,切削速度100 m/min,切削进给量0.1 mm/r条件下的涂层结合强度等值线,如图5所示。 图5a中,ap=0.1 mm条件下,等值线分布均匀,加工涂层结合强度随着f的增大而减小,切削速度对结合强度影响较小。图5b中在0.1 加权综合评分法是多指标正交试验分析的常用方法[7],其计算公式如式(6)所示。 Mi=bi1Mi1+bi2Mi2+…+bijMij (6) 式中:bij为权因子系数,表示各项指标在综合加权评分中占的权重;Mij为考察指标,i为表示第i号实验,j为表示第j考察指标。其中,权因子系数可根据实际加工涂层的使用要求、专业知识、生产经验进行权重的分配。 假设某一利用热喷涂修复的轴类零件,涂层结合强度是涂层表面质量首要考虑指标,只有涂层结合强度满足一定要求才能保证涂层具有足够的使用寿命。其次考虑的指标是表面粗糙度,表面粗糙度在满足使用要求的范围内即可使用。因此设表面粗糙度的权重为40%,涂层结合强度的权重为60%,利用加权评分法可得表8所示结果。从表中可以看出1号实验加权总分最高,因此可以认为在综合考虑表面粗糙度和加工后涂层结合强度的情况下,采用切削深度0.1 mm,进给量0.1 mm/r,切削速度100 m/min的切削参数可以得到最符合要求的表面质量。 (1)采用正交试验法对Fe基涂层切削加工后表面粗糙进行测量,研究了切削参数对加工表面粗糙度的影响,结果表明切削进给量是影响表面粗糙度的最主要因素,其次为切削速度、切削深度。在所选水平中的最佳加工方案为:ap=0.2 mm,f=0.1 mm/r,v=140 m/min。 表8 加权综合评分法分析结果 (2)对切削加工后的涂层结合强度进行测量,建立了切削参数与对加工后涂层结合强度影响的预测模型。结果表明切削深度是影响涂层加工后结合强度的主要因素,最优加工方案为切削深度0.1 mm,切削进给量0.1 mm/r,切削速度100 m/min。建立的预测模型可以较为准确的预测加工后涂层的结合强度。 (3)利用加权综合评分法进行工艺优化,设置不同的表面粗糙度值及结合强度权重,根据加权总分可以选择出符合表面质量要求的切削参数。 [1]徐滨士. 中国再制造产业及再制造技术新进展[J]. 热喷涂技术, 2010, 2(3): 1-6. [2]徐维普, 徐滨士, 张伟. 高速电弧喷涂涂层的结合强度与结合方式研究[J]. 热加工工艺, 2007, 36(7): 62-64. [3]Wang Min, Xu Binshi, Dong Shiyun, et al. Experimental investigation into the effect of cutting parameters on cutting forces in turning of Fe-based amorphous overlay for remanufacture[J]. International Journal of Advanced Manufacturing Techonlogy (article in press), 2013:1-9. [4]Zhang X C, Xu B S, Wang H D, et al. Thermo-mechanical integrity of coatings with residual stresses[C]. Fracture Mechanics 2004-Symbosium of Environment Effects on Fracture and Damage, Huangshan, China, 2004: 225-240. [5]张以鹏. 实用切削手册[M]. 沈阳: 辽宁科学技术出版社, 2007. [6]张甲英, 赵刚, 丁华东, 等. 回转体零件热喷涂涂层的结合强度[M]. 中国表面工程, 2014, 27(2): 19-23. [7]邱轶兵. 试验设计与数据处理[M]. 合肥: 中国科学技术出版社, 2008.

3.2 涂层结合强度测量及分析




3.3 工艺优化
4 结语