基于干扰排队模型的LNG船舶进出港效率分析

张晓东， 张浩， 陈伟炯， 肖英杰

(1．上海海事大学 商船学院，上海 201306； 2.上海海事局，上海 200086)

0 引 言

提高港口航道危险品运输保障能力和通航效率是“公路水路交通运输十二五发展规划”的核心任务.[1]液化天然气(Liquefied Natural Gas,LNG)船舶具有高危险性和排他性，会对港区船舶交通安全和进出港通航效率造成不同程度的不利影响.LNG船舶进出港口航道时如发生事故，轻者将造成船舶损伤，阻碍港口交通，重者将造成液化气泄漏，导致船舶爆炸和环境污染.这不仅会造成重大的人员伤亡和财产损失，还会产生恶劣的社会影响.在我国，由于LNG船舶运输的危险性较高，海事监管要求严，船舶进港引航难度大，进港和靠泊要求非常高，需由巡逻船护航、消防拖船伴航和船舶交通服务(Vessel Traffic Services,VTS)严密监控.LNG船舶的进出港和靠泊安全直接关系到我国港口的能源安全.我国近年来在辽宁大连鲶鱼湾、河北唐山曹妃甸、青岛胶南董家口、江苏洋口、上海洋山、浙江宁波北仑、福建莆田、广东珠海高栏岛、深圳盐田、海南洋浦等港口建立LNG接收站,未来几年LNG船舶将以超过平均每2天1艘次的频率进出我国沿海港口，每次进港需近5 h交通管制时间，而随着水上运输业的发展，进出港航道上船舶通航密度也在逐年增大，这使发生危险品运输船舶事故的风险越来越大.LNG船舶进出港的安全和效率问题已经成为摆在国家和海事管理部门面前的一个突出问题.

我国学者在LNG船舶运输安全和效率方面的研究已取得显著成果：邬惠国等[2]提出基于格序决策理论的LNG船舶进出港组织方案比选；徐国裕[3]提出增进高雄港VTS水域交通安全和效率的模型，对台湾海域及高雄港水域的海难事故进行分析，对船舶交通安全度和船舶通航效益进行定量化研究,未涉及危险品运输；刘敬贤[4]基于港口系统船舶排队仿真模型对大型海港进港主航道通过能力及交通组织模式进行研究，解决常态交通条件下船舶进出港的效率问题，未涉及LNG船舶运输安全问题；周世波等[5]和熊振南等[6]针对湄洲湾水域设计LNG船舶监管方案仿真系统，实现船舶航行环境可视化仿真；宋向群等[7]对复杂条件下沿海港口深水航道通过能力及航道线数进行研究，以提高通航效率为主，解决通过设计航道提高航道通过能力的问题；ZHENG等[8]提出随机条件下天然气运输网络扩展和LNG终端位置最优化规划的风险管理模型和算法；CHENG等[9]提出融入直觉模糊集的事故树模型寻找LNG码头应急关闭系统的脆弱点并进行改进；ELSAYED[10]提出基于模糊推理系统的LNG船舶装卸货物风险评估系统；DEBNATH等[11]借鉴道路交叉口交通冲突的原理，通过研究船舶在警戒区交汇水域内的相互作用, 提出基于碰撞分析的水上交通风险模型；MAVRAKIS等[12]提出包含海峡特性描述、海峡通过规则和交通统计特征的仿真模型，同时把安全因素整合到安全通航规则中；OZBAS等[13]提出分析船舶交通影响因素(包括航道交通规定、规则船型、货物类型、气象、地理环境、引航和拖船服务)的仿真平台.综上所述，离散事件仿真模型已广泛应用于通航效率分析，通过排队论模型计算船舶平均到达率、海峡入口船舶平均等待时间、船舶平均通过航道时间、船舶在锚地平均等待时间等，但在多种外界干扰条件下的排队论模型鲜有研究.

1 多类型干预的单服务台排队模型

船舶在航道进口处往往因拥挤等多种原因产生船舶在锚地排队等待问题.各种气象或灾害条件下的交通管制策略使得估计船舶的等待时间非常困难.过境船舶随机到达港口后在锚地排队等待直到被允许通过，每次只允许一艘船舶进入航道.当交通情况受到能见度低、风、浪、流和船舶交通事故等因素干扰时，若有一艘船舶已经进入航道，一般不会在航道中停止运行，以免对其他船舶和环境造成碰撞风险；而在锚地等待队列中的船舶不能进入航道直到条件恢复正常.本文提出一个干扰排队分析模型，估计船舶在航道入口点的平均等待时间.

1.1 基本进出港排队模型

船舶到达规律指船舶通过某特定水域的时间分布规律或单位时间内通过的特定船舶数量随时间变化的规律.船舶通过特定水域的时间是不确定的，到达方式有如下特点：在某段时间内到达的船舶数量仅与这段时间的长短有关；在不相交的时间区间内到达的船舶数量相互独立；船舶的到达有先后次序，不存在2艘以上的船舶同一时间到达的情况.

上述特点恰好满足排队论的基本条件，即为随机到达.因此，船舶的到达分布可用泊松分布描述，其基本公式为

式中：t为每个计数间隔持续的时间;P为在t内通过或到达k艘船的概率；λ为平均船舶到达率.

1.2 干扰排队模型

LNG船舶进出港常遇到多种干扰情况，如出现恶劣天气和发生交通事故等.考虑2种不同的干扰形式：单干扰和多干扰.单干扰指系统在一个时刻只有一个干扰发生，如只发生交通事故或只出现恶劣天气.多干扰指同一时刻不同干扰完全重叠或部分重叠.本文采用ULUSÇU等[14]提出的“完成时间法”获得期望的船舶排队等待时间.服务完成时间C定义为从连续发生船舶服务开始到下艘船舶开始接受服务的时间.无干扰发生时，服务完成时间等于服务时间;有干扰发生时，服务完成时间大于服务时间.已经在航道中的船舶受到干扰后，剩下的服务要到该服务完成才结束，因此定义实际服务时间为Sa.

1.2.1 两种不同类型的干扰

考虑两种不同类型的干扰:非同时干扰和同时干扰.

1.2.1.1 非同时干扰下的排队等待时间

非同时干扰指一个干扰发生时，其他干扰在条件恢复正常前不发生，即系统在一个时刻只有一个干扰发生，无重叠.同时干扰指服务台受到同时发生的不同类型干扰，即同一时刻不同干扰完全重叠或部分重叠.定义W为到达船舶排队等待时间，N为排队等待的船舶数量,E[C]为期望服务完成时间，E[W]为期望排队等待时间.

过程描述:如果服务台空闲，到达的船舶立即开始接受服务；如果服务台忙，到达船舶等待直到当前的船舶服务完成；如果船舶到达时服务台中断，船舶等待直到服务台恢复正常.后到达的船舶要依次排队等待直到前面所有的船舶服务结束，而可能的干扰造成的中断都可能发生在他们的服务完成前.到达船舶的排队等待时间

W=N×C=

式中:Cr为船舶到达时余下的服务完成时间;Yri(i=1,…,k)为船舶到达时服务台中断服务导致的余下中断时间.

船舶到达时由于干扰i服务台中断的概率为

期望排队等待时间为

式中:ρa=λE[Sa].

1.2.1.2 同时干扰下排队等待时间

服务台受到多个干扰，各干扰相互独立，可能同时出现,此情况下到达船舶排队等待时间为

W=N×C=

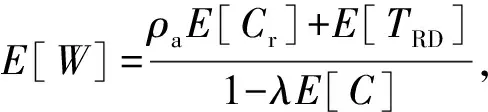
1.2.1.3 服务完成时间

服务完成时间由实际服务时间Sa和服务中断时间TDS构成,

E[C]=E[Sa]+E[TDS]

以两种不同类型的干扰为例，分别定义干扰1和干扰2，可能的情况见图1～3.

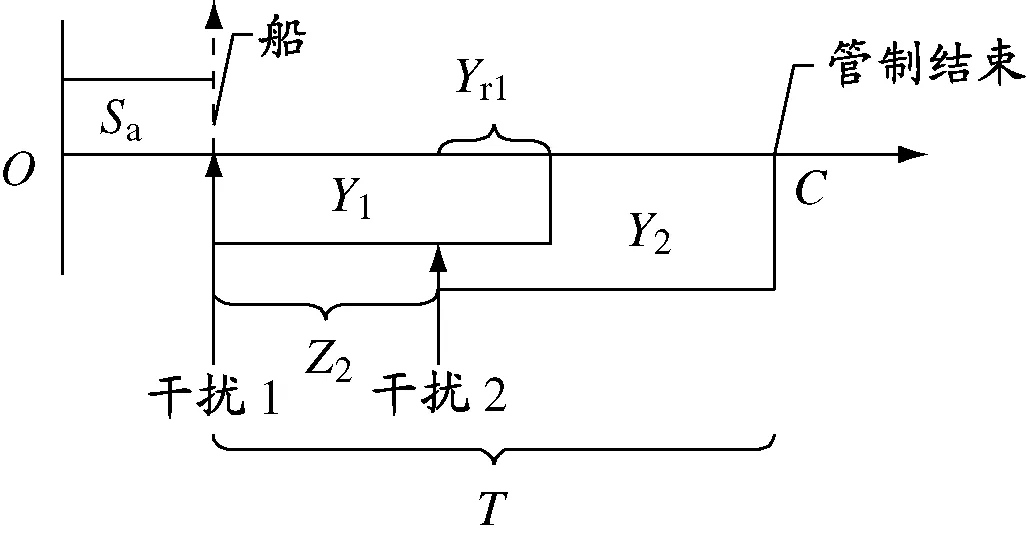
图1 TDS(两种干扰同时发生且Yr1≤Y2)

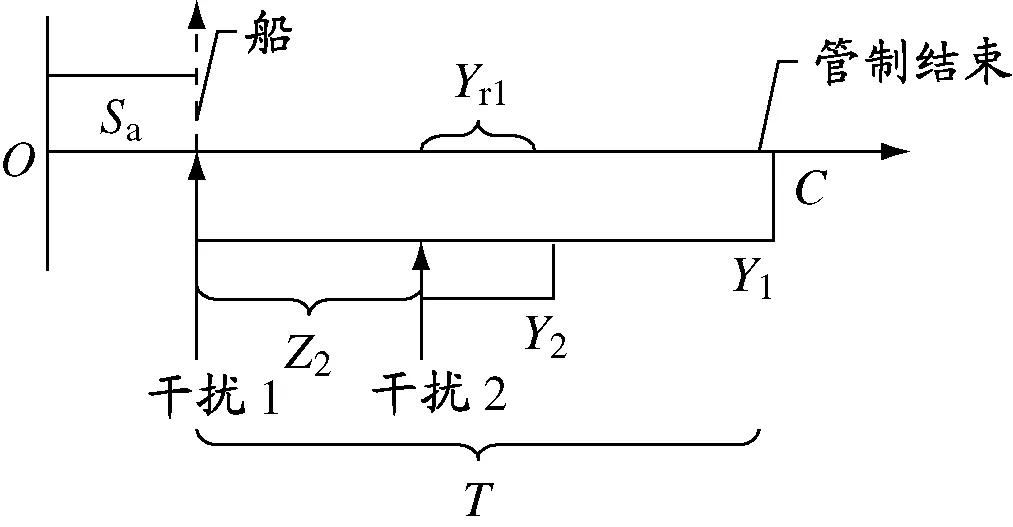
图2 TDS(两种干扰同时发生且Y r1>Y2)

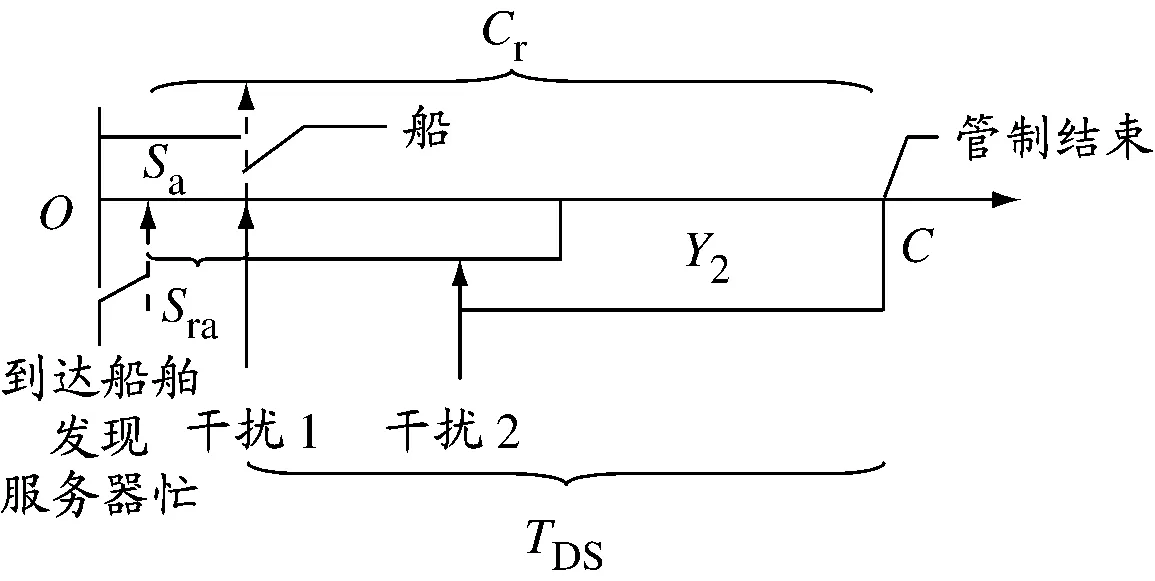
图3 余下服务完成时间Cr

1.2.2 3种不同类型的干扰

实际中发生干扰的类型一般不超过3种，因此选择3种干扰进行分析，见图4～6.

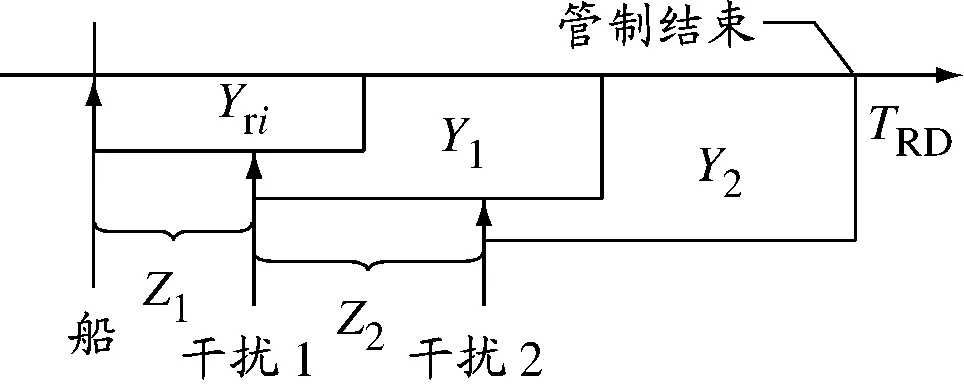
图4 一种干扰发生其他干扰跟着发生时的TRD

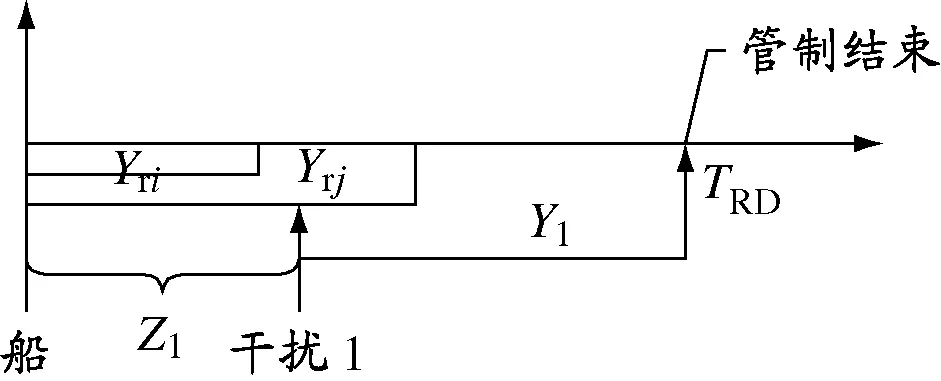
图5 两种干扰发生第3种干扰跟着发生时的TRD

2 案例分析

采用离散事件仿真的排队论理论研究LNG船舶进出港的规律(如队长分布、等待时间分布等)和排队系统的最优设计，反映LNG船舶进出港的主要特性和状态，分析进出港交通效率.设置仿真周期为1年，初始条件为无干扰发生情况.

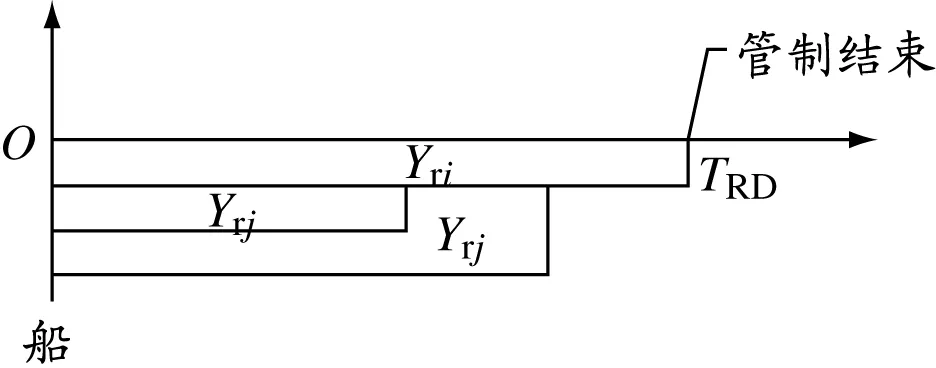
图6 3种干扰同时发生时的TRD

2.1 模型输入

输入信息见表1.

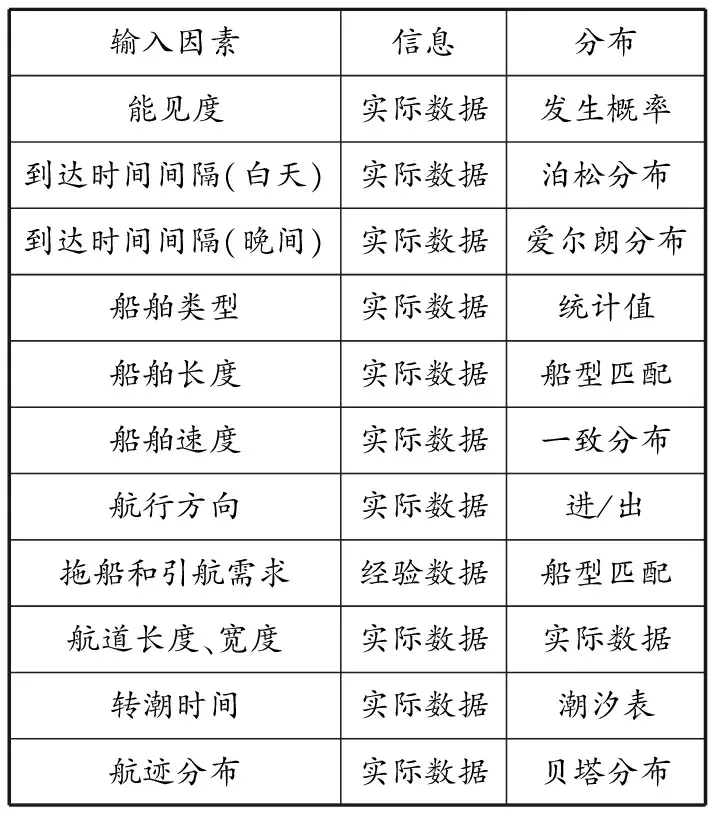
表1 输入信息

2.2 干扰排队模型

LNG船舶进出港干扰排队过程见图7.

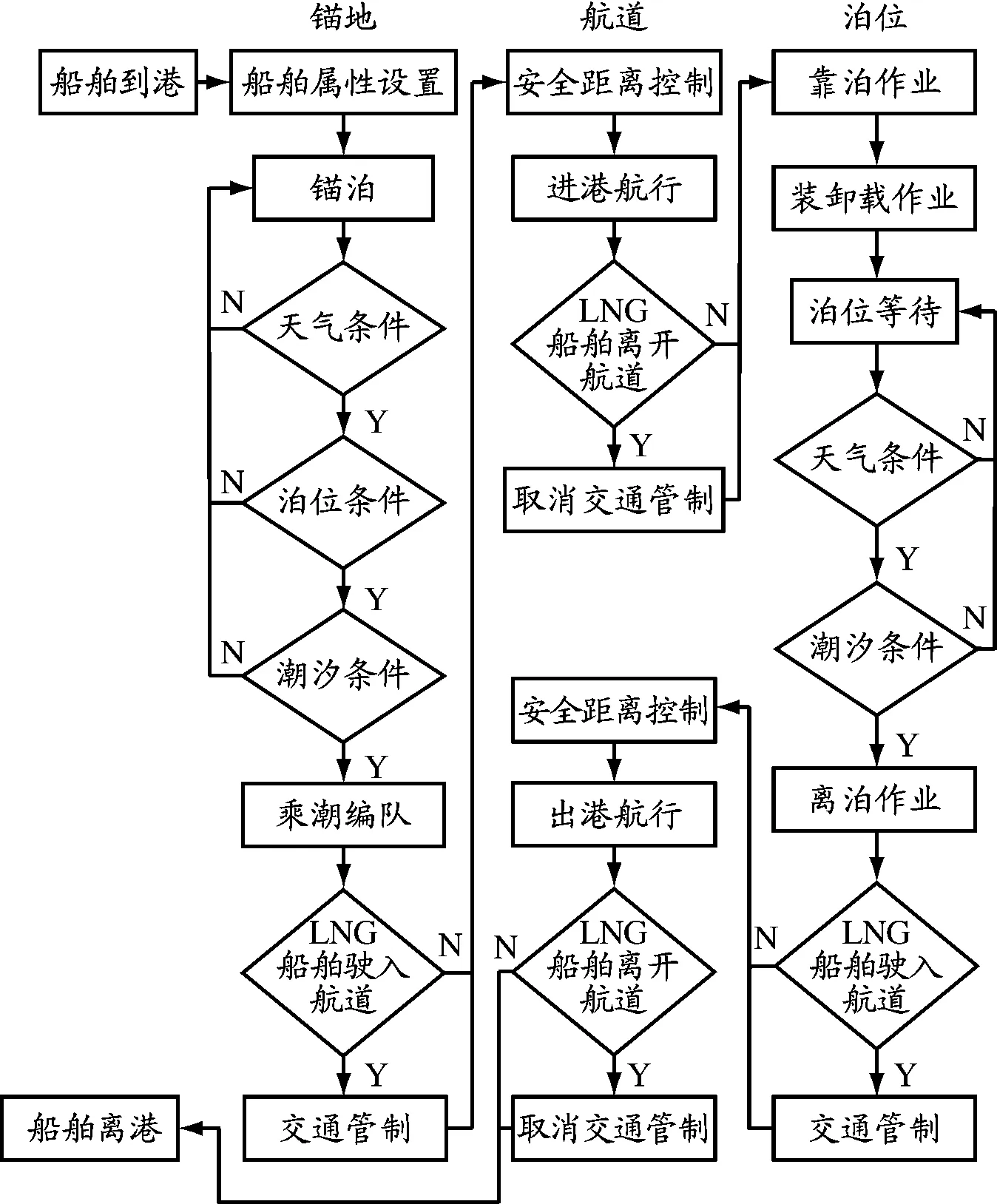
图7 LNG船舶进出港干扰排队过程

系统中根据船舶在港内的位置和工作状态，主要设置如下排队事件:(1)LNG船舶到达锚地事件.把船舶放入等待泊位的队列中，记录船舶到港时间.(2)船舶锚泊成功事件.把船舶放入等待航道的队列中，记录锚泊时间.(3)船舶进入航道事件.把仿真期内每个潮汐的振幅按时间先后顺序排成一个队列形成潮汐列表，用来辅助仿真系统判断航道的通航情况；把船舶放入航道中的队列中，记录船舶进入航道的时间并计算离开航道的时间.(4)可能的干扰事件.服务时间服从任意分布，进出港船舶遵守先到先服务原则，本文假设该仿真实验的服务时间服从泊松分布.假设该服务器受多种不同类型的干扰,中断发生次数服从指数分布，中断时间服从任意分布.定义排队模型中的船舶服务时间为从第1艘船进入航道到第2艘船距离第1艘船满足最小间隔距离进入航道时第1艘船航行的时间(此时第1艘船仍在航行).针对国内某港口进港航道实际统计，2艘船的间隔发生距离大约0.5 n mile，间隔时间大约5 min.因此，航道进口船舶交通排队模型可看作是受多种干扰的单服务器单级排队无限队长模式.(5)船舶靠泊事件.船舶离开航道，把船舶放入相应的泊位中，记录船舶靠泊时间并计算船舶计划离泊的时间.(6)船舶离泊事件.船舶进入航道离港，把船舶放入航道中的队列中，记录船舶进入航道的时间并计算离开航道的时间.

2.3 仿真结果

仿真实验数据与实测数据对比见表2.

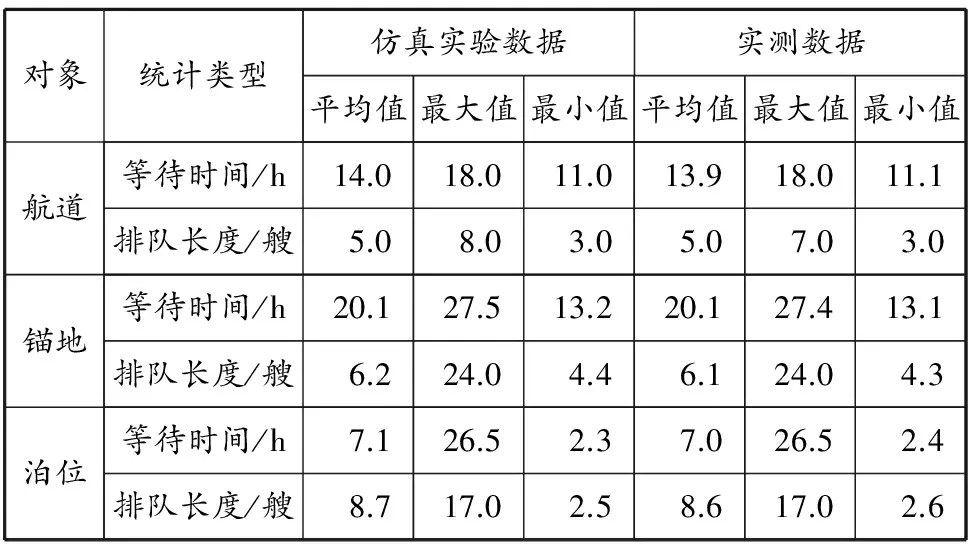
表2 仿真实验数据与实测数据对比

针对仿真所依据的逻辑模型、基本设定、仿真过程及仿真结果，干扰排队模型能较好地模拟航道船舶的通过状况，与实际情况较匹配，可为LNG船舶进出港安全和效率评价提供非常重要的技术手段.仿真算例结论与实测的定量分析结论基本一致.

3 结束语

LNG船舶的增加给港口带来的压力已很明显，通过加深和拓宽航道及锚地等基础设施在相对短时间内提高航行安全和通行能力显得不太现实.本文在考虑影响效率因素基础上提出改进的基于干扰的排队模型具有实际意义.

参考文献：

[1]交通运输部. 公路水路交通运输“十二五”规划确定五个重点领域[EB/OL]. (2010-09-02)[2013-09-25]. http://www.gov.cn/gzdt/2010-09/02/content_1693849.htm

[2]邬惠国, 刘春姣, 肖英杰. 基于格序决策理论的LNG船舶进出港组织方案比选[J]. 上海海事大学学报, 2012, 33(2): 10-13.

[3]徐国裕. 增进高雄港VTS水域交通安全和效率的研究[D]. 大连: 大连海事大学, 2009.

[4]刘敬贤. 基于船舶行为特征的港口航道通过能力仿真[J]. 大连海事大学学报, 2009, 35(2): 31-37.

[5]周世波, 熊振南. 湄洲湾LNG船监管方案仿真系统设计与实现[J]. 上海海事大学学报, 2009, 30(4): 52-56.

[6]熊振南, 周世波. 船舶航行环境可视化仿真[J]. 上海海事大学学报, 2009, 30(1): 6-9.

[7]宋向群, 张静, 郭子坚, 等. 通航历时对沿海散货港区航道通过能力的影响分析[J]. 港工技术, 2010(2): 18-20.

[8]ZHENG Q P, PARDALOS P M. Stochastic and risk management models and solution algorithm for natural gas transmission network expansion and LNG terminal location planning[J]. J Optim Theory Appl, 2010, 147(2): 337-357.

[9]CHENG Shuen-Ren, LIN Binshan, HSU Bi-Min,etal. Fault-tree analysis for liquefied natural gas terminal emergency shutdown system[J]. Expert Systems with Applications, 2009, 36(9): 11918-11924.

[10]ELSAYED T. Fuzzy interference system for the risk assessment of liquefied natural gas carriers during loading/offloading at terminals[J]. Appl Ocean Res, 2009, 31(3): 179-185.

[11]DEBNATH A K, CHIN H C. Navigational traffic conflict technique: a proactive approach to quantitative measurement of collision risks in port waters[J]. J Navigation, 2010, 63(1): 137.

[12]MAVRAKIS D, KONTINAKIS N. A queueing model of maritime traffic in Bosporus Straits[J]. Simulation Modelling Practice & Theory, 2008, 16(3): 315-328.

[13]OZBAS B, OR I, ULUSCU O S,etal. Simulation-based risk analysis of maritime transit traffic in the strait of Istanbul[J]. Int J on Mar Navigation and Safety of Sea Transportation, 2009, 3(3): 295-300.

[14]ULUSÇU Ö S, ALTIOK T. Waiting time approximation in single-class queueing systems with multiple types of interruptions: modelling congestion at waterways entrances[J]. Annals Operations Res, 2009, 172(1): 291-313.