基于列生成算法的集装箱班轮运输网络优化

吴琼, 郑士源, 朱太球

(1. 上海海事大学 交通运输学院, 上海 201306; 2. 浙江荣盛控股集团 人力资源部, 杭州 311247)

0 引 言

随着航运市场的实时变动，集装箱班轮运输网络优化成为很多航运公司需要面对的重要问题.集装箱班轮航线优化是运输网络优化的一部分.CHRISTIANSEN等[1]建立的班轮模型计算量大使得越来越多的班轮运输网络优化模型相继出现，班轮运输网络的优化更加复杂化，运输网络优化的模型规模也逐渐加大.目前求解大型运输模型的方法主要有枚举法、贪婪算法、列生成算法和Benders分解算法.枚举法求解运输模型效率较低，贪婪算法随着模型规模的增大求解速度和准确性降低.CHUANG等[2]通过包含有5个港口的小型案例解释说明他们的遗传算法，其目的是通过在不确定性部分运用遗传算法与在离散部分运用遗传算法相结合求出需求不确定时的最优航线.GELAREH等[3]运用Benders分解原则求解模型并求出转运港位置以及辐射港与转运港连接的类型.本文采用启发式列生成算法对运输网络模型分块求解，既能提高求解效率又能增强求解结果的准确性.

1 问题提出

在集装箱班轮运输中运输路径和货物运量决定航运联盟可以从此运输网络中获得的收益.这两者高度相关而且需要同时考虑，因此决策变量即为运输路径和货物运量.在以利润最大为目标函数的同时，需要考虑以下约束：每段航线和港口货物运量的平衡、船队运能约束、运输需求约束以及承运人船舶数量的约束.[4]本文根据设计模型的特点，选择启发式列生成算法，可以大幅减小模型规模，有效减少计算时间，并利用IBM-ILOG优化平台和IBM-ILOG CPLEX优化引擎实现该算法，实验计算表明该算法具有较高运算效率，能为求解大规模的航线网络优化问题提供一种可行有效的方法.[5]

2 模型建立与求解

2.1 参数假设

在集装箱班轮运输网络优化中可以忽略的因素[6]：(1)不考虑时间成本，即不考虑船舶在航行过程中因为时间问题产生的成本；(2)为简化计算，每一类船舶在规划子航线上的航次成本为现有航线上航次成本的平均值；(3)船舶的可变成本指在同一条航线上运输空集装箱的费用，在本文中忽略此费用[7]；(4)以现有航线的起始港与目的港之间的需求为主，假设每个转运港口的货物装卸数量相等，即转运港口达到货物运量均衡.

2.2 模型建立

航运联盟航线优化的目标函数是利润最大.[8]现将模型[9-10]建立如下：

opt(X(o,d,m))

(1)

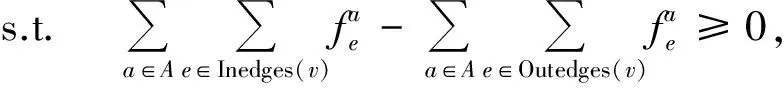
∀v∈V,∀(o,d,m)∈Θ

(2)

X(o,d,m)≤0， ∀e∈E,∀(o,d,m)∈Θ

(3)

(4)

(5)

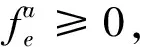
(6)

X(o,d,m)=0,1

(7)

式(2)中，经过港口v的所有航线组成网格，例如经过港口4的航线有1-2-4-6，1-3-4-7，1-4-5，则Inedges(4)={2-4，3-4，1-4}，Outedges(4)={4-6，4-7，4-5}.

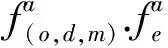
该问题主要有6个约束：式(2)表示网络中每个转运港的货物运量平衡，保证每个转运港的装卸平衡；式(3)为供应约束，表示每条航线的货物运量必须小于所有船舶的总运能；式(4)为需求约束，表示o-d之间的所有规划子航线的货物运量小于o-d之间的货物需求量；式(5)为船舶数量约束，即在规划子航线(o,d,m)上运营的最多船舶数量要小于船舶的总数量；式(6)和(7)是对决策变量的取值范围的约束.

2.3 列生成算法

2.3.1 算法比较

贪婪算法指先求出一个可行初始解，然后根据这个可行初始解进行最优化测度.贪婪算法步骤：第一步，建立数学模型描述问题；第二步，把求解问题分为若干个子问题；第三步，对每一个子问题求解，得到子问题的局部最优解；第四步，把子问题的局部最优解合成原来问题的一个解.从中可以看出该算法需要求解多个局部最优解，比枚举法有一定的优势但仍需大量的计算，不能直接排除不良的局部最优解；而列生成算法在这些方面进行改进.因此，选择列生成算法进行求解.

2.3.2 列生成算法

列生成算法在求解大规模混合整数规划问题上具有突出的优势.考虑到航线优化模型规模非常大，假设航运网络中有7个港口，模型变量即达到几十种之多，如果需要求解更大规模的问题，经常会超过软件规模限制，因此设计更精巧的算法是实现模型实用化的关键.列生成算法是数学规划求解方法中经常采用的方法之一，其特点是在需要的时侯生成有价值的变量.采用列生成算法可以有效减小模型规模、提高运算效率.

列生成算法将原线性规划问题分为主问题和子问题.由于主问题变量数目巨大，选择部分变量(至少包含一个可行解)作为限制主问题(Restrained Main Problem, RMP).主问题的规模尽可能小(假设每个装货港到卸货港之间只由1艘船运送集装箱)，求解RMP到最优，将得到的对偶变量值传递给子问题，求解子问题形成具有正简约成本的列(目标函数为最大)，将正简约成本最大的列加入RMP中，继续求解RMP.重复上述过程，直到子问题不能产生正简约成本的列为止，此时原问题达到最优。如果原问题需要求得整数解，再利用分支定界法进行求解.[12]

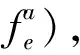
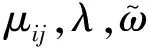
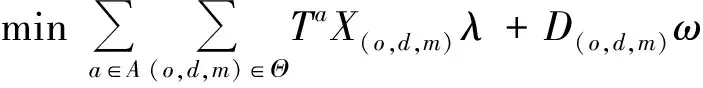
(8)

(9)

(10)

(11)

将初始X(o,d,m)代入RMP求得决策变量和对偶变量的值.下面构造价格子问题.

式(9)的经济意义为将航运网络的成本与运送集装箱的边际成本进行比较.

(12)

式(12)的经济意义为对于运输网络上的运输路径如果存在3类船舶货物运输的边际收益高于目前运输方案的边际成本，则该运输路径可以改变主问题的目标函数值，因此可以考虑运用式(12)作为列生成算法子问题的依据.利用式(9)对所有的路径进行检验，以保证每条路径的货物运量都满足需求约束.最优情况即运能等于需求，即不等式取等.综上考虑，列生成算法的子问题可以表示为

(13)

(14)

(15)

该算法实现步骤如下：

步骤1选择初始解，根据选择初始航线的规则初步选定航线P0.用k表示当前迭代次数，k=0，构建简化的X(o,d,m)矩阵.

步骤3求解子问题，遍历搜索所有的路径.依次检验是否满足式(14).如果满足式(14)，寻找能够运输该o-d虚拟货物的船舶a∈A，判断是否满足式(15)；如果满足式(15)，则对可能的判断是否满足式(13)；如果满足式(13)则为主问题找到一个新的列变量，否则继续搜索下一个可能的组合.如果本组已搜索完毕，则继续寻找下一个a；遍历所有的船舶-o-d后，若能找到新变量，转步骤4；若没有找到新变量，则主问题已满足最优条件，转步骤5.

步骤5求解恢复整数约束的主问题，并报告最终求解结果.

3 案例分析

结合第2节的数学模型理论，将这些理论运用到实际案例CKYH联盟中，以进一步验证其优越性并提出相应的经营策略.

3.1 已知参数

3.1.1 航线和港口的选取

选取CKYH联盟从亚洲到地中海的4条航线(ABX，AMX，AES3，MD3)进行研究[13]，根据对这4条航线上的各港口每年吞吐量的分析，运用Container Forecaster 11.4Q估算得出2013年CKYH联盟在这4条航线上的航次货物运量，见表1.

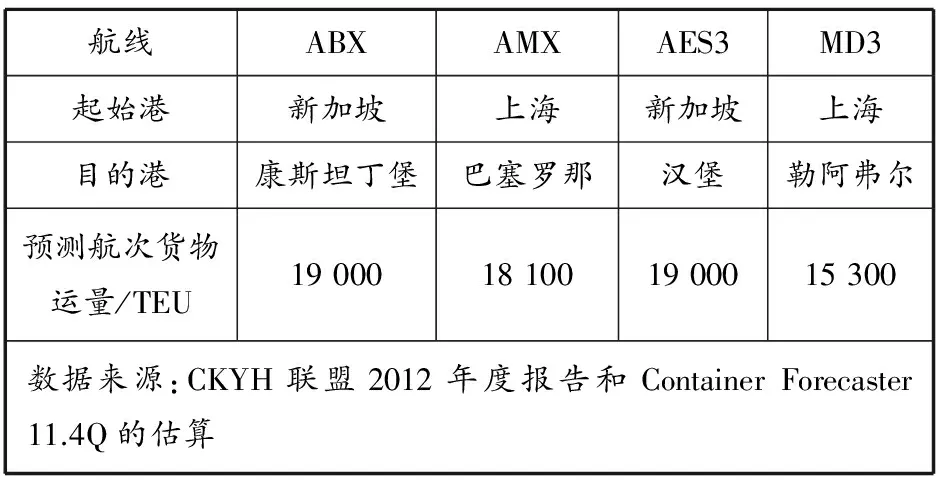
表1 CKYH联盟在亚洲到地中海的运营航线概况

根据航线初选的原则，选择包括这4条航线的起始港和目的港在内的7个港口进行航线优化.这7个港口分别为上海、新加坡、康斯坦丁堡、巴塞罗那、鹿特丹、汉堡和勒阿弗尔.为表达简便，设定这7个港口的代码依次为1，2，…，7，那么这4条航线对应4个o-d对，分别为2-3，1-4，2-6，1-7.

3.1.2 CKYH联盟运能概况

由于CKYH联盟在2012年5月开始与长荣海运合作远东至地中海区域的航线，统计资料也将长荣纳入其中.CKYH联盟船队规模统计见表2.

表2 CKYH联盟船队规模分类统计

根据CKYH联盟在亚洲-地中海航线上的货运量占全球的比例分配船舶，为简化计算，假设CKYH联盟在亚洲到地中海运营的船舶类型为5 800，3 700，2700 TEU,即T1=5 800 TEU，T2=3 700 TEU，T3=2 700 TEU，对应的船舶数量分别为225，117，110艘，即N1=225艘，N2=117艘，N3=110艘.

CKYH联盟在7个港口之间的货物运价见表3.船舶在运输的过程中肯定会产生一些费用，如船员工资、修理费、港口使费、船舶燃料费等，而且为更新设备或扩大再生产，还有机器折旧费.为支付这些费用并创造效益，航运公司就要向货主收取一定的费用(即运费).运费单位价格就是运价，也就是说运价是单位运输产品价值的货币表现.[12]

表3 任意两个港口之间的货物运价 万美元/TEU

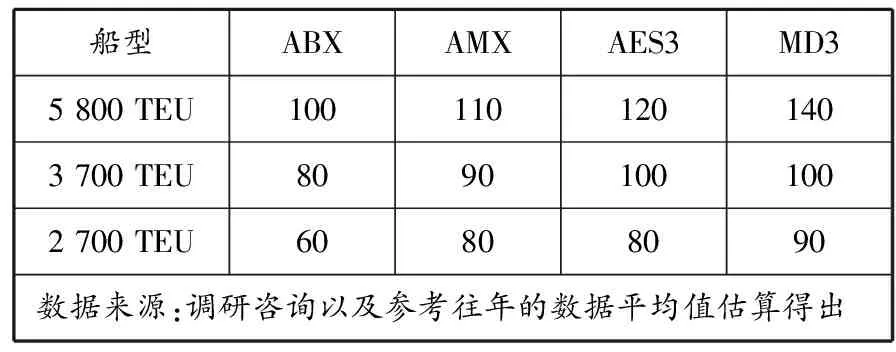
表4 每条航线的航次固定成本 万美元/航次

在实际计算中可以把规划子航线的航次成本看作是经过规划子航线的现有航线航次固定成本平均值.每艘船舶在某航线上往返航次成本包括海上航行和港口停靠所产生的直接或间接总费用.

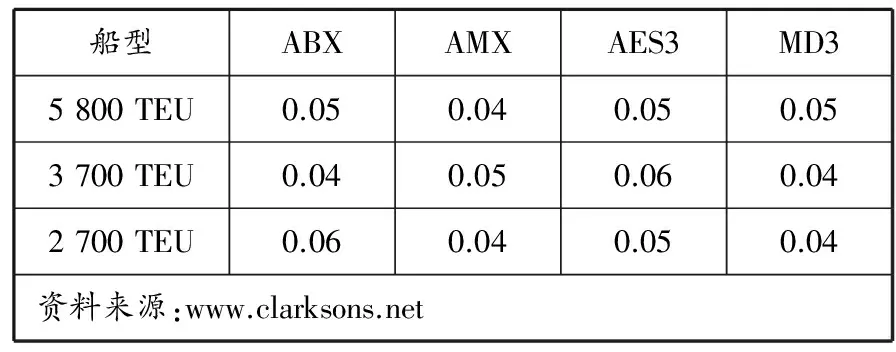
表5 不同船型在每条航线上的单位成本 万美元/TEU

4 结果分析

按照第3.3节所述流程运用CPLEX编程进行求解，结果见表6.

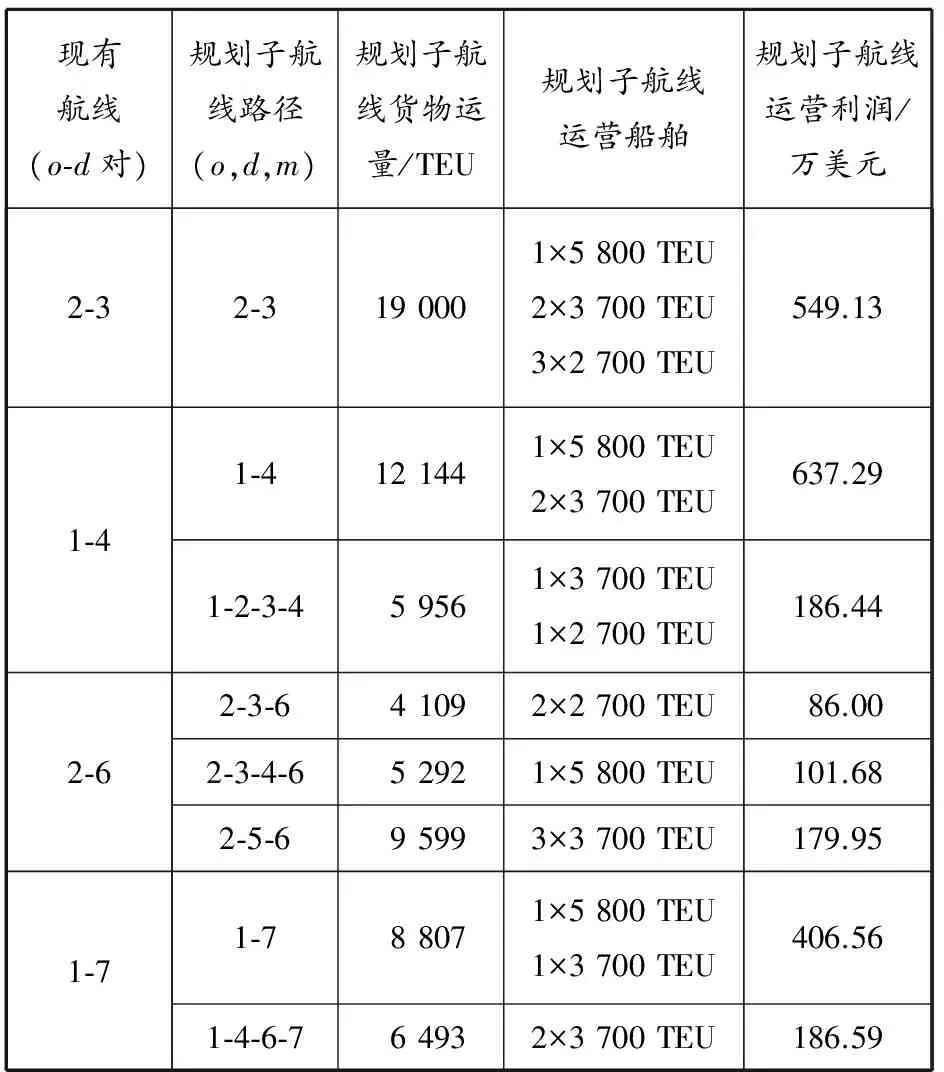
表6 CKYH联盟亚洲-地中海航线网络优化结果

总利润为所有规划子航线的利润之和.本文的规划子航线有8条(见表6)，计算可得maxz=1 772.93万美元，联盟需要4艘5 800 TEU，11艘3 700 TEU和3艘2 700 TEU的船.

5 结论与展望

本文根据列生成算法求得CKYH联盟在亚洲到地中海的最佳航运网络，使联盟利润达到最大，可为CKYH联盟和其他集装箱班轮运输公司提供一定的参考依据.本文得出结论：(1)集装箱班轮运输网络中的一些港口之间的货物运量可以通过调整航线和运营船舶进行交叉运送，初始港与目的港之间的货物运量可以分为多条路径和多艘不同类型船舶进行运输，这样可以节省成本并减少航次时间和资金浪费.[14](2)列生成算法对于航运网络优化问题是适用的.当混合整数规划模型中存在大量的块结构并且列数大于行数(即决策变量多于约束条件)时可以采用列生成算法；为节省时间提高效率可以采用启发式列生成算法.为算法设定特定的循环程序可以更快地求解.

本文仅选取含有7个港口的案例，运用启发式列生成算法可以很快求得结果，但当问题规模变大时该算法是否适用还有待进一步研究.另外，本文是对航运联盟整体进行网络优化，航运联盟要保持稳定就必须满足每个成员的利益并形成一定的机制[15]，所以列生成算法是否也能运用到每个成员的航线优化也待进一步研究.

参考文献：

[1] CHRISTIANSEN M, FAGERHOLT K, NYGREEN B,etal. Handbooks in operations research and management science: transportation[J]. Maritime Transportation, 2007, 14: 189-284.

[2] CHUANG T N, LIN C T, KUNG J Y,etal. Planning the route of container ships: a fuzzy genetic approach[J]. Expert Systems with Applications, 2010, 37(4): 2948-2956.

[3] GELAREH S,PISINGER D. Fleet deployment, network design and hub location of liner shipping companies[J].Transportation Res,2011, 47(6): 947-964.

[4] 吴文一. 航运联盟下的集装箱运输路径选择研究[D]. 上海: 上海海事大学, 2004.

[5] AGARWAL R, ERGUN Ö. Ship scheduling and network design for cargo routing in liner shipping[J]. Transportation Sci, 2008, 42(2): 175-196.

[6] LU H A. Modelling ship’s routing bounded by the cycle time for marine liner[J]. J Marine Sci & Technol, 2002, 10(1): 61-67.

[7] SHINTANI K, IMAI A, NISHIMURA E,etal. The container shipping network design problem with empty container repositioning[J]. Transportation Res Part E: Logistics & Transportation Rev, 2007, 43(1): 39-59.

[8] 陈继红, 真虹, 宗蓓华. 班轮配船模型的改进及其在航运联盟箱位租用中的应用[J]. 交通运输系统工程与信息, 2008, 8(3): 120-125.

[9] 杨秋平. 船队规划数学建模与算法研究[D]. 大连: 大连海事大学, 2010.

[10] 张华歆. 逆向物流的网络结构和设计[D]. 上海: 上海海事大学, 2004.

[11] CHU C W, KUO T C, SHIEH J C. A mixed integer programming model for routing containerships[J]. J Mar Sci Technol, 2003, 11(2): 96-103.

[12] 蓝伯熊, 吴李知. 铁路客运网络列车开行方案优化模型的列生成算法研究[J]. 运筹与管理, 2012, 21(1): 1-10.

[13] 任斐. 集装箱班轮航线靠港选择模型问题研究[D]. 大连: 大连海事大学, 2007.

[14] CHRISTIANSEN M, FAGERHOLT K, RONEN D. Ship routing and scheduling: status and perspectives[J]. Transportation Sci, 2004, 38(1): 1-18.

[15] 郑士源. 合作博弈理论的研究进展——联盟的形成机制以及稳定性研究综述[J].上海海事大学学报, 2011, 32(4): 53-59.