运力供需失衡时集装箱班轮航线配船优化

靳志宏， 李娜， 韩骏,2， 邱波,3

(1. 大连海事大学 交通运输管理学院，辽宁 大连 116026； 2. 中国海运(香港)控股有限公司，香港 999077；3. 中远散货运输有限公司，北京 100024)

0 引 言

作为国际贸易的派生需求，国际航运业的发展取决于国际贸易的发展，而集装箱班轮运输市场作为国际航运市场最重要的子市场，是全球经济贸易变化最直接、最敏感的“温度计”.基于航运市场270余年的数据统计，航运市场的变化呈现周期性，每一周期都经过波谷、增长、波峰、衰退等4个阶段，期望周期为7～11年.本轮周期始于2003—2007年，在此期间航运市场得到快速发展，航运市场的火爆致使班轮公司纷纷扩张运力，在2008年达到波峰；受2008年由美国次贷危机引发的全球金融危机的影响，集装箱班轮运输需求大幅下降，供需严重失衡，运价大幅下滑，2009年达到波谷；2010年，在各国经济刺激举措下，全球经济开始走出低谷，全球贸易量呈恢复性增长，集装箱运输市场也不同程度回暖，国际集装箱市场供需关系总体上相对平稳.2011年至今，受欧洲债务危机的影响，主要发达经济体的经济复苏和发展中经济体的经济增长均有所减缓，不确定因素增加，航运市场仍然处于缓慢复苏之中.

从集装箱运量供给方面看，受造船周期长、运力供给滞后于运力需求变化的影响，近年来集装箱运力供给一直保持着快速增长，集装箱市场出现运力供过于求的状态，且这一状况会在今后一段时期内长期存在.德鲁里航运咨询公司的数据显示，全球船舶供过于求的状况将延续至2015年.

面对班轮运输市场供需失衡的状况，班轮公司在市场低迷时需要采取相应的经营策略，其中降低航速和闲置运力便是其主要经营策略.例如，亚欧航线上集装箱船的航速在金融危机爆发前普遍为24～25 kn，危机爆发以来各船公司普遍将航速降至12～14 kn.另外，班轮航线具有很强的稳定性，一旦开辟航线，在相当长的一段时间内不宜变更.航运危机期间航运业不仅面临着外部需求的减少，且航运业内部正在消化鼎盛时期盲目扩张造成的运力过剩压力.

关于集装箱班轮航线方面的研究主要包括两大方面：其一是航线网络设计、船队规模确定[1]、挂靠港口选择、挂靠顺序优化、服务频率设定等；其二是航线配船，即在现有船队规模前提下，决定各航线配置的船型、各船型配置数量、运力闲置船型及数量等.前者属于战略层面的航线规划与设计问题，后者则属于运作层面的调度优化问题.本文研究的内容属于后者.

国外关于航线配船方面的研究起步较早.PERAKIS等[2]和JARAMILLO等[3]针对船公司现有航线网络，基于航运需求预测，将航线配船问题分别归结为线性规划与混合整数规划问题.CHO等[4-5]针对某集装箱班轮企业筛选出若干条备选航线，利用线性规划模型优化航线，在此基础上采用混合整数线性规划模型对更大规模船队进行运营优化研究.POWELL等[6]针对航线配船问题构建混合整数规划模型，通过模型求解给出各船舶的挂靠顺序，并据此决策船公司的船队规模.

国内关于航线配船方面的研究相对较晚.杨华龙等[7]建立航线配船问题的线性规划数学模型，探讨最优船型配置问题.徐天芳等[8]分别针对两点往返型航线、环型航线、钟摆型航线提出运量、运力平衡方法.李智等[9]采用神经网络算法求解班轮航线配船优化模型.赵刚等[10]对上海电煤长江运输系统的航线配船问题进行优化.林珈伊等[11]研究内河航运中受船闸时间阻抗变动影响下的配船问题，建立非线性配船模型.靳志宏等[12]结合班轮航运市场的上行、下行周期，分别构建多航线多船型的自有、租用联合分配优化模型.

在当今的航运市场，减速航行作为一种运营手段，一方面可以降低燃油成本，另一方面也可以吸收过剩运力，保持一定的发船频率，确保减速但不影响服务质量.CHRISTIANSEN等[13]归纳近年来不定期船和班轮在减速航行领域的研究成果.杨秋平等[14]分析航速变化对航次时间、航次成本、航线配船数量等规划决策产生的非线性影响，但缺乏班轮航线船舶发船频率的约束，也没有考虑航速变化对实际运营成本的影响.NORSTAD等[15]研究不定期航线航速变化对航次成本与配船数量的影响，以航速为变量构建数学模型.文献[14-15]提供的模型和方法更适合于不定期船舶运输.MENG等[16]以降低日运营成本为目标，提出单一集装箱航线上航速与配船数量和类型的解决方法.

基于航运业的运力供需失衡的行业现状及其研究现状，本文构建以航速和运营船舶数量为决策变量的运力过剩时的班轮航线运力配置优化模型，开发禁忌搜索算法对模型进行求解，基于实际航线的大规模数值试验显示该模型及算法的有效性.

1 供过于求时的班轮航线配船建模

1.1 班轮航线配船概述

班轮航线配船是将班轮船队中不同类型、不同载箱量的集装箱船舶配置到公司经营的各条航线上，在运力供不应求时使整个船队效益最大，在运力供过于求时使运营成本最低.主要包括单航线多船型、多航线单一船型和多航线多船型几种情形.航线配船除应满足挂靠港以及船舶本身的硬件和技术方面的需求外，还应遵循整个航线网络系统优化、按照船期表准班运行、同一航线船型相近以及大船配干线等原则.

除满足上述航线配船硬性条件及软性约束外，集装箱航线配船的影响因素还包括沿线各港口货运需求量、发船频率、航线距离等.

1.2 航线配船建模前提条件

基于班轮航线运营的现实状况，航线配船建模约定如下前提条件：(1)航线配船计划期以年为单位计算；(2)计划期内公司自有船舶的数量一定，根据运力需求租入或闲置相应船型的船舶；(3)航线上各挂靠港口顺序一定，航次时间等同于同一船舶相邻两次同向挂靠同一港口的时间；(4)航速并不取决于舱位利用率及额定装载量，同一航线配置的船舶航速相同；(5)航线沿线各港口间货流量可预测；(6)经营成本项包括船舶固定成本(船舶租金或折旧、人员工资等与航次无关的所有费用)和航次变动成本(燃油费和港口使费).

1.3 模型符号说明

集合符号：K为船队所有船舶类型的集合，K={k∈K|k=1,2,…}；R为船队历经的所有航线集合，R={r∈R|r=1,2,…}.

决策变量：xkrs为分配在航线r上以s档次的速度运营的k型船的数量，其中，s是离散值，表示航速档次，相邻航速档次之间的差别对应于航线上多配一条船和少配一条船的差别；yk为k型船的年闲置数量；zrs当航线r上船舶以s档次的速度运营时取值为1，否则取值为0.

Ir为航线r上的港口数量；Nk为k型船的拥有量；Gr为航线r的发班频率；i为港口编号，若i是航线r上的挂靠港，则i=1,2,…，Ir；Nkrs为k型船在航线r上以s档次的速度运营时的年航次数，

Nkrs=Tr/Tkrs

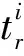
其中：Fk为k型船的日固定成本，fk为k型船航行时重油的日消耗量，gk为k型船在航行时发电机燃料(轻油)的日消耗量，P为重油的燃料价格，P′为发电机燃料价格，Dkr为k型船在航线r上每航次的港口使费.

1.4 目标函数与约束条件

由于在当前及今后相当长一段时期内航运市场会持续处于运力大于运量的状态，加之集装箱船舶大型化等因素推动，航运公司的运营策略是在满足用户货运需求的前提下尽可能降低总的配置成本，因此，基于航速的运力配置目标是运营成本与船舶闲置成本之和最低，目标函数为

约束条件为

(1)

(2)

(3)

xkrs,yk≥0且为整数,zrs为0-1变量

(4)

式(1)指配置在航线r上的船舶数量需满足该航线发班频率的要求；式(2)为确保满足每一种类型的船舶数量约束；式(3)保证同一航线上的船舶采用同一航速运行；式(4)为混合整数规划的变量约束.

2 供过于求时班轮航线配船优化算法设计

2.1 航线配船中禁忌搜索算法的要素设置

(1)解的表示形式.本文使用实数编码，编码的每一位就是解的相应维的取值.利用三维矩阵表示k型船分配在航线r上以s档次的速度运营的船舶数量，设置r=0的航线为虚拟航线，将闲置的船舶分配到该航线上.

(2)初始解的产生机制.基于班轮航线配船的特点，同一条航线上的船舶以相同的航速运营，即同一条航线上只有某一航速档次上有船舶分配，而其余航速档次上没有船舶分配；另外，鉴于每一条航线的发船频率由该航线的运力需求决定，可以事前给定，因此对于非全零的那一行，其数值之和是一定的；最后，基于航运公司在航运下行期的运营策略，初始解设计时以较大的概率选择较低的航速档次.

(3)邻域解的生成.一般的组合优化问题邻域解的生成通常采用相邻交换、随机插入和随机交换等3种产生机制构造邻域结构，这些方法比较适合于0-1决策变量，对于航线配船问题并不适用.本文基于航线配船问题的特殊性，设计3种邻域变化算法：①交换随机选定的两条航线上的配船方案；②交换同一航线不同航速档次间的配船方案；③交换同一航线已配航速档次下两种船型数量.

(4)其他要素.直接选择目标函数作为评价函数，基于问题自身的特点，设置两个禁忌表：一个存放禁忌解X，另一个存放解向量对应的目标值B(X).解禁规则采用基于目标函数值的准则，即若某个禁忌对象的目标值优于当前最优解，则解禁此候选解，并将其作为当前解，将此候选解的评价值作为新的当前最优解.终止准则为设定最大迭代步数.

2.2 航线配船的禁忌搜索算法主体步骤

班轮航线配船的禁忌搜索算法主体步骤如下：

Begin

令LT(tabu list)=空集；给定初始解Xnow；计算目标函数值B(X)；Bbest=Bnow=B.

Do

采用3种邻域构造方式构造总数为n个Xnow的邻域解N(Xnow)；计算目标值B(X)，按B值降序对N(Xnow)排序，排序后记为X′；

For eachX′ inN(Xnow)

IfX′ not inHthen

H中插入X′；

Xnow=X′；

Bnow=B；Exit For；

Else

IfB>Bbestthen

H中解禁X′；

Xnow=X′；

Bnow=B；Exit For；

End

While循环次数内；

ReturnXbest，Bbest；

End

3 算例验证

3.1 数据采集

大规模模拟实验采用当前产业界的6种主力船型，参数见表1；采用7条代表性航线，编号为1，2，…，7，依次为东南亚/美西航线，中国/西北欧航线，中国/美西航线，远东/地中海美东航线，中国/澳大利亚航线，中国/南非、南美东航线以及中国/海湾航线，参数详见表2；各航线航速档次及其对应所需船舶数量和最大年航次数见表3.

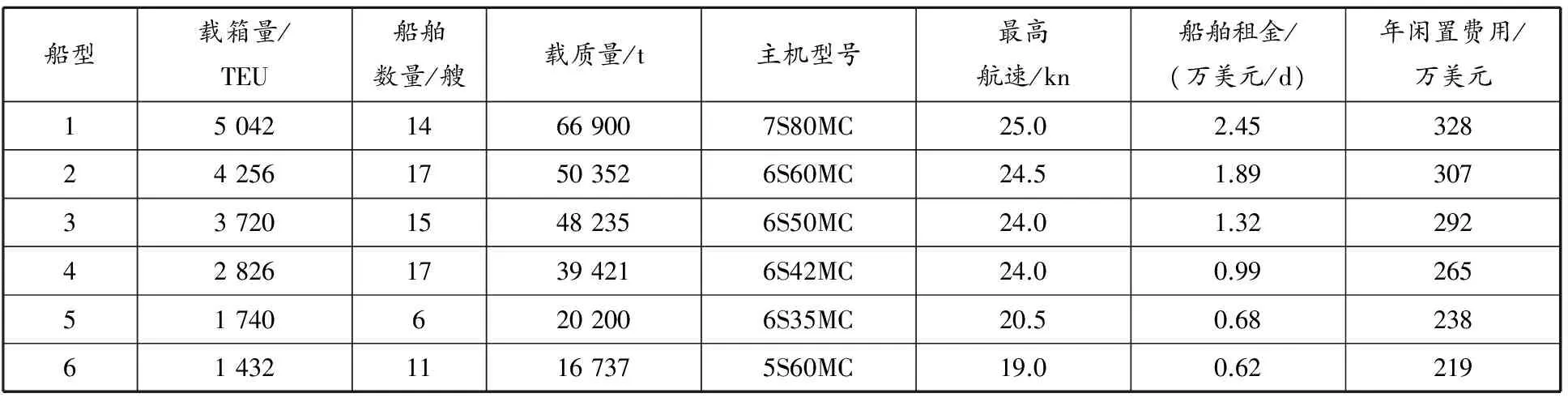
表1 船型参数

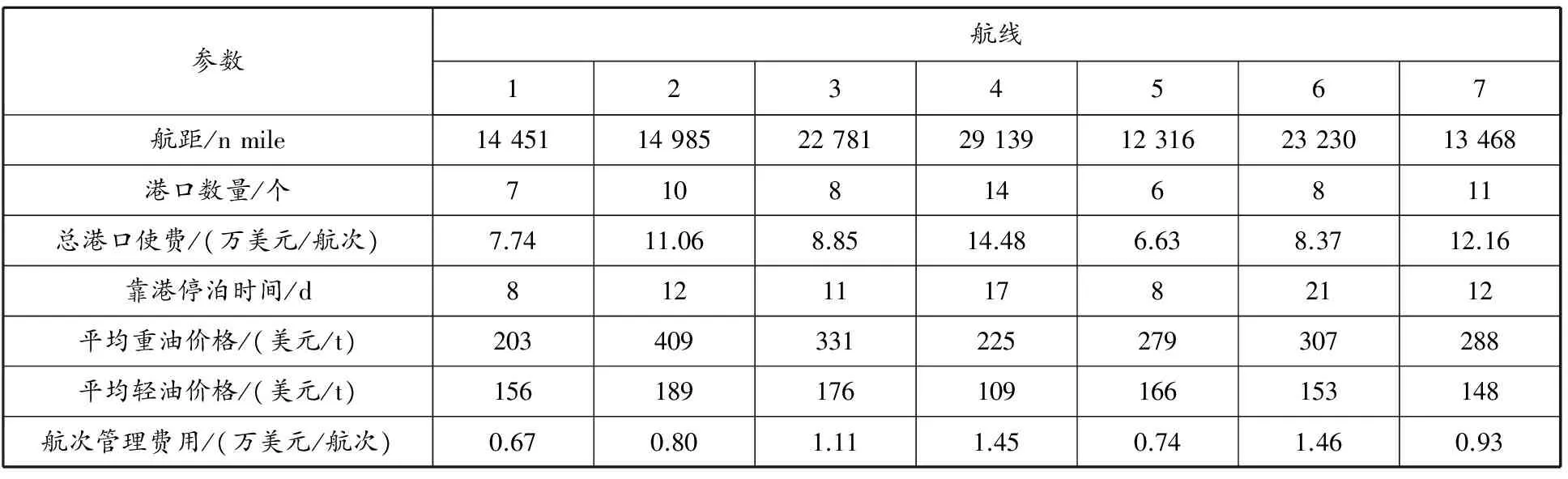
表2 7条代表性航线参数

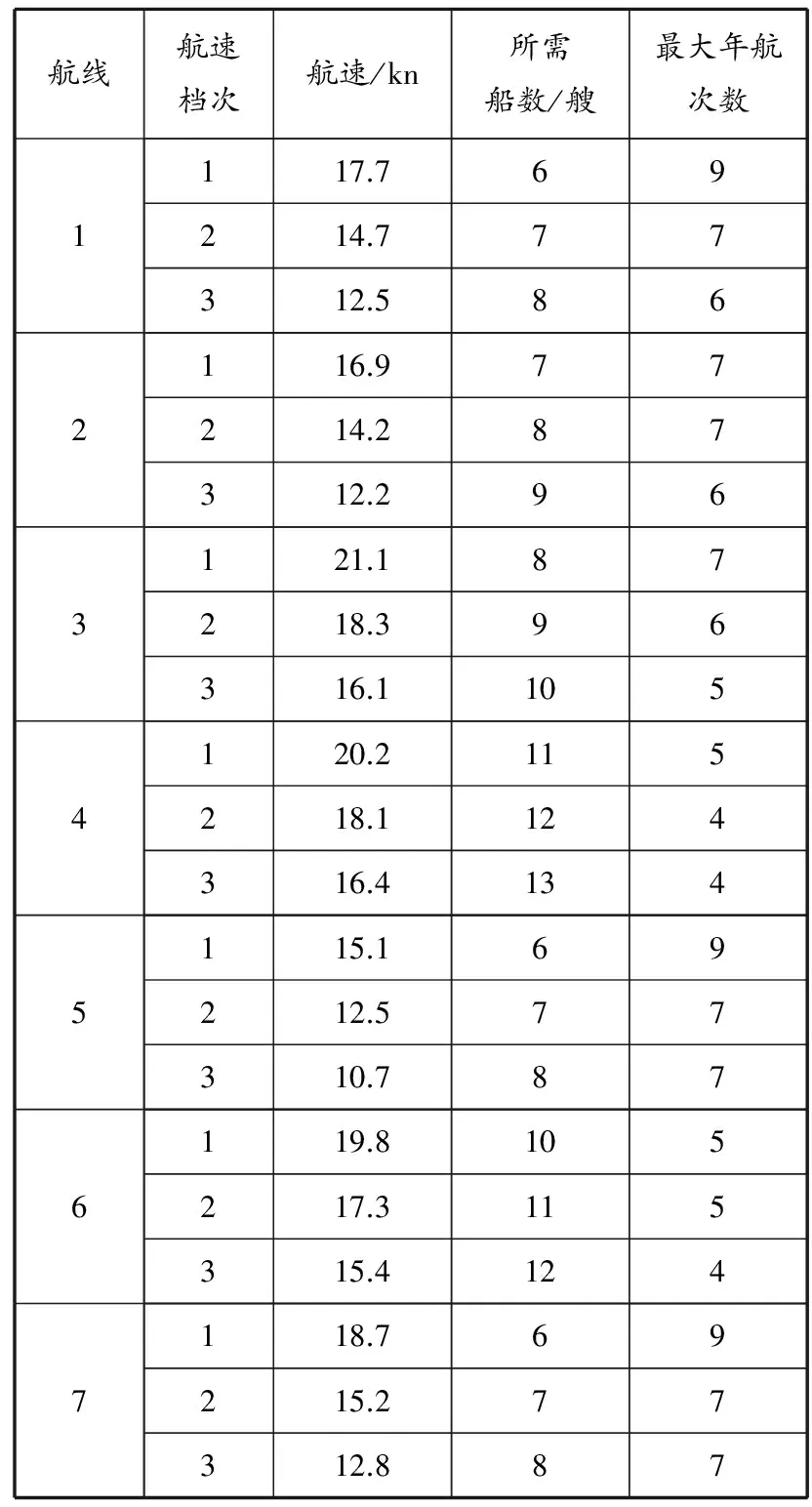
表3 航线要求

3.2 结果与分析

基于上述模型计算航次成本，见表4.将上面的船型、航线参数以及各航线的航次成本计算结果作为禁忌搜索优化算法的输入，得到优化配船结果见表5.

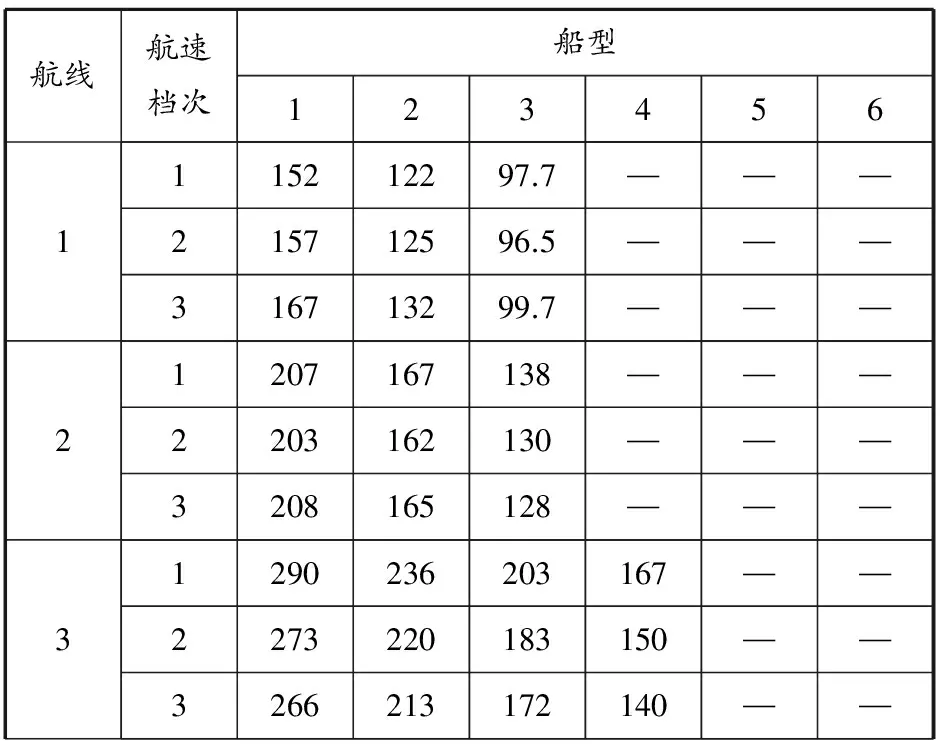
表4 7条航线航次成本 万美元

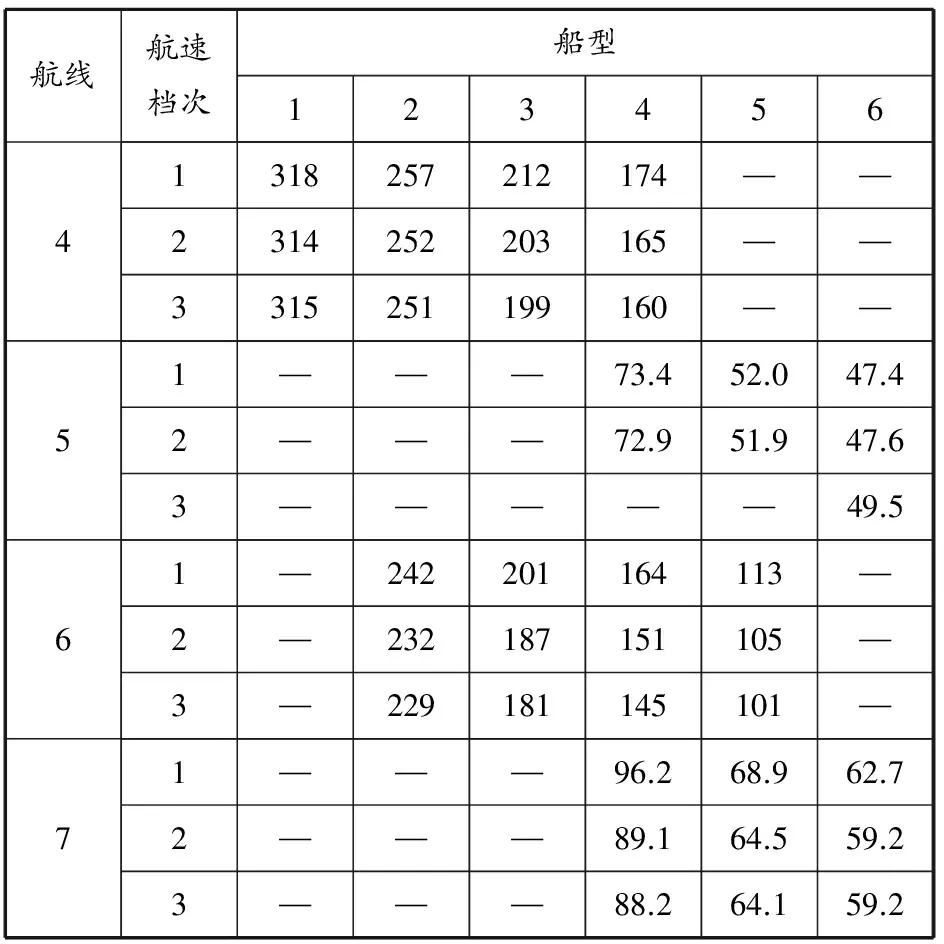
续表4

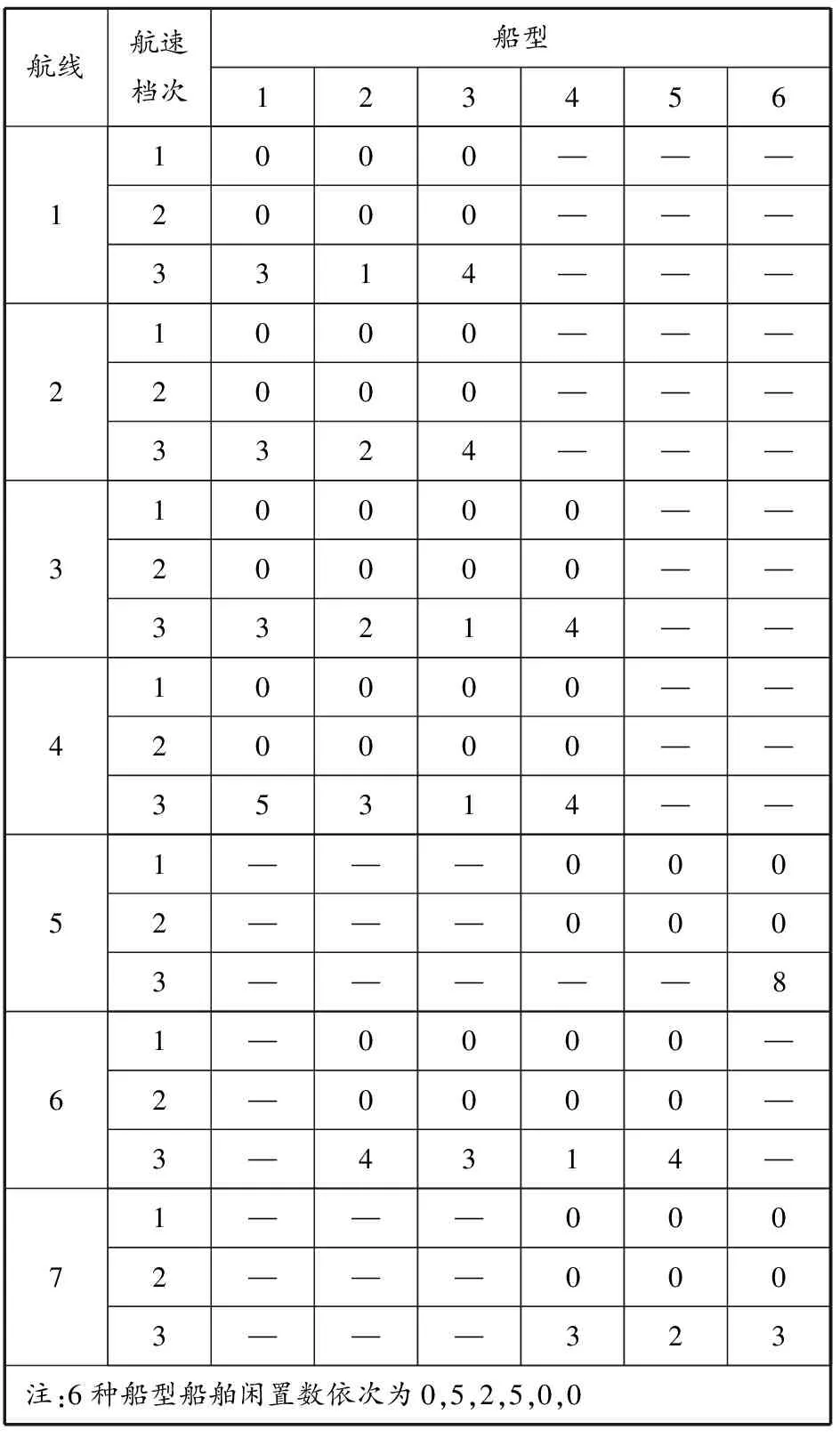
表5 7条航线的配船结果

从表5的优化配船结果来看，7条代表性航线上尽管船型和航速不同，但采用的均是各船型的低速档次(第3档次航速)航行；同时，航线1～4的配船结果与实用配船经验“长线大运量配大船”相一致；航线5，7的配船结果也反映“短线配小船”的经验做法；另外，对介于这两者之间的航线(如航线6)，其配船优化结果也恰恰是船型权衡折中的结果；最后，从闲置船舶的船型及数量看，也是各种航线配船影响因素综合作用的结果.因此，本文提供的方法可为配船决策者在这种“两难”的决策中提供量化支持.

4 结束语

由美国次贷危机引发、欧债危机持续等所导致的航运危机使集装箱班轮运输市场的航运需求萎缩以及由造船周期长等导致的运力供给较之于运力需求的滞后性，使得全球航运市场运力与运量的供需严重失衡，减速航行与闲置运力成为航运企业面临的关键决策.本文通过构建以航速和运营船舶数量为决策变量的运力过剩时的班轮航线运力配置优化模型并开发求解算法，为集装箱班轮公司采取低速航行、闲置运力提供决策支持.进一步的研究将集中于上述优化模型的实证研究方面.

参考文献：

[1] 杨秋平, 谢新连. 多种类型投资的船队规划模型[J]. 上海海事大学学报, 2010, 31(1): 61-66, 80.

[2] PERAKIS A N, JARAMILLO D I. Fleet deployment optimization for liner shipping part 1: background, problem formulation and solution approaches[J]. Maritime Policy and Manage, 1991, 18(3): 183-200.

[3] JARAMILLO D I, PERAKIS A N. Fleet deployment optimization for liner shipping part 2: implementation and results[J]. Maritime Policy and Manage, 1991, 18(4): 235-262．

[4] CHO S C, PERAKIS A N. Linear and integer linear programming models for container liner fleet routing strategy[J]. Maritime Policy and Manage, 1994, 21(1): 35-61.

[5] CHO S C, PERAKIS A N. Optimal liner fleet routing strategies[J]. Maritime Policy and Manage, 1996, 23(3): 249-259.

[6] POWELL B, PERKINS A N. Fleet deployment optimization for liner shipping: an integer programming model[J]. Maritime Policy and Manage, 1997, 24(2): 183-192.

[7] 杨华龙, 钟铭. 集装箱班轮航线配船优化决策研究[J]. 大连海事大学学报, 1996, 22(3): 51-54.

[8] 徐天芳, 胡丽娜. 国内班轮航线配船研究[J]. 大连海事大学学报, 2000, 26(2): 53-55.

[9] 李智, 陈明昭, 董治德. 基于神经网络的班轮航线配船优化方法[J]. 交通与计算机, 2000, 18(1): 34-36.

[10] 赵刚, 祁斌. 上海电煤长江运输系统航线配船优化[J]. 上海海事大学学报, 2004, 25(3): 51-55.

[11] 林珈伊, 陶桂兰. 船闸阻抗影响下的内河航线非线性配船模型[J]. 上海海事大学学报, 2012, 33(2): 14-17.

[12] 靳志宏, 李娜, 陈梦. 基于航运周期的班轮航线运力配置优化[J]. 武汉理工大学学报: 交通科学与工程版, 2012, 36(2): 219-222.

[13] CHRISTIANSEN M, FAGERHOLT K, NYGREEN B,etal. Ship routing and scheduling in the new millennium[J]. Eur J Operational Res, 2013, 228(3): 467-483.

[14] 杨秋平, 谢新连, 裴光石. 考虑船舶航速的船队规划非线性模型[J]. 华南理工大学学报:自然科学版, 2011, 39(10): 119-126.

[15] NORSTAD I, FAGERHOLT K, LAPORTE G. Tramp ship routing and scheduling with speed optimization[J]. Transportation Res Part C: Emerging Technologies, 2011, 19(5): 853-865.

[16] MENG Q, WANG T. A scenario-based dynamic programming model for multi-period liner ship fleet planning[J]. Transportation Res Part E: Logistics and Transportation Rev, 2011, 47(4): 401-413.