导弹配平飞行数值模拟及控制优化

达兴亚，陶 洋，赵忠良，马晓永

（1.空气动力学国家重点实验室，四川 绵阳 621000；2.中国空气动力研究与发展中心 高速空气动力研究所，四川 绵阳 622661）

0 引 言

传统上以定常气动力和动导数数据建立气动力模型，通过计算机仿真设计和检验飞行器控制律［1－2］。这是一种基于线化假设的气动、飞行力学分析方法，由于没有计入非定常、非线性气动力效应，在描述机动飞行时具有很大的不确定度［3－4］。依据线性理论设计的控制方法在试飞后可能需要作出较大幅度修改。

虚拟飞行数值模拟［5－7］是计算流体力学与飞行力学交叉的新方向，是解决先进飞行器的气动／运动耦合问题及控制问题的新途径。计算流体力学能够模拟非线性、非定常气动力效应，它与刚体六自由度运动方程耦合计算，能更好地反映实际飞行过程。尽管虚拟飞行数值模拟技术还面临一些技术上的困难［7］，但已有一些应用，如外挂分离［8］、导弹受控飞行［5，9－10］、自由飞［11］、飞机受控飞行［6，12］。近年来，国内对集成CFD、飞行力学和自动控制律的虚拟飞行技术产生了浓厚的兴趣，并已有初步应用。然而，这些工作基本是不带控制［13－14］或开环控制［5，15］，对闭环控制仿真的研究较少。

本文在现有虚拟飞行数值模拟程序VFNS（Virtual Flight Navier－Stokes solver）［15］基础上，应用虚拟飞行技术来检验和优化导弹模型纵向配平飞行PID控制律，研究闭环控制模拟的可行性和参数影响。

1 虚拟飞行数值模拟方法及检验

控制方程为非定常RANS方程和刚体六自由度运动方程，采用基于结构嵌套网格的有限体积求解器，取Roe格式和S－A湍流模型，时间推进使用双时间步，采用嵌套网格方法模拟舵面偏转；飞行力学方程采用Adams预估校正法求解，气动／运动耦合使用双时间步三阶Adams预估校正策略，预测步计算格式为：

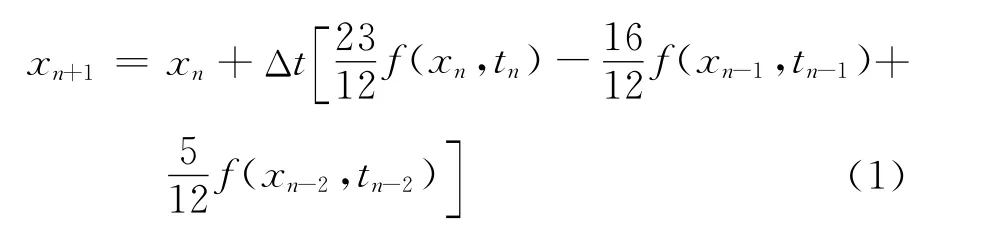
修正步计算格式为：

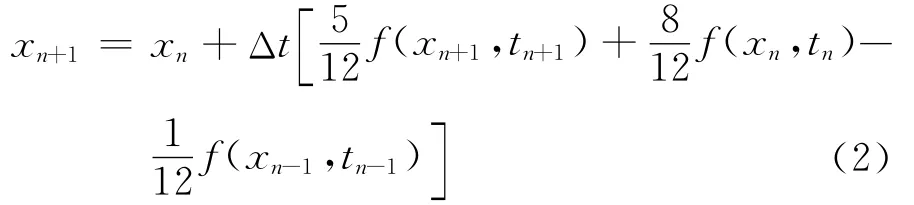
研究表明，这种耦合方法在保证一定计算精度条件下，能显著增大时间步长，有利于缩短CFD计算时间，从而显著提高计算效率。具体流场／飞行力学计算方法和结论见文献［13］。

模拟了窄条翼布局导弹纵向开环虚拟飞行，外形与图1类似。弹身采用标准对接网格，尾舵采用嵌套网格，总量约620万，首先让俯仰舵在0.3s内偏转－2°，然后保持4s。计算 Ma＝0.6，从图2看出，在舵偏期间，试验、仿真、模拟结果吻合很好，说明较好地捕捉到了模型的非定常气动特性，验证了计算方法和网格，可以用于此条件下的闭环控制模拟。

图1 窄条翼布局导弹－IRIS－TFig.1 Strake missile（IRIS－T）

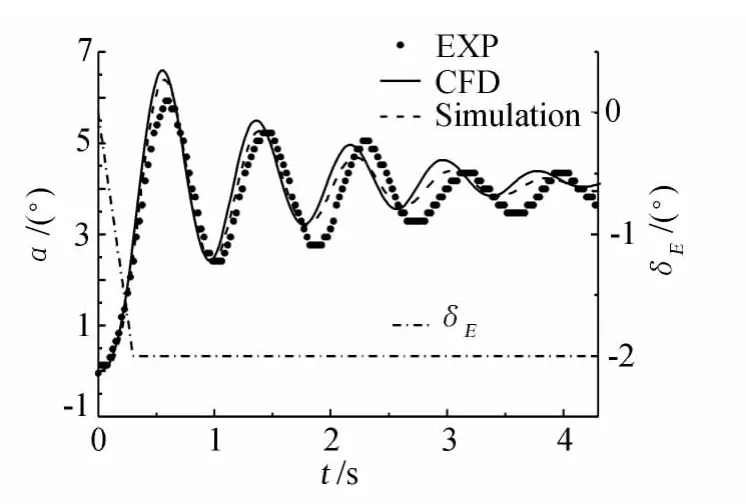
图2 纵向虚拟飞行数值模拟结果Fig.2 Longitudinal virtual flight simulation result

2 配平飞行PID控制模拟

2.1 控制方法

以迎角为控制对象，给定目标迎角α0，采用单位负反馈，对俯仰舵偏角δE实施PID控制，控制框图如图3所示，其中简化了舵控系统。这里PID控制器

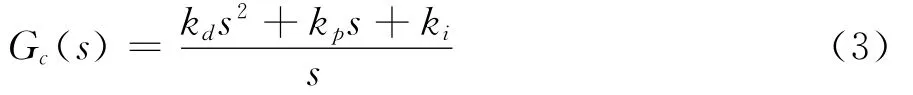
kp、kd、ki分别为比例、微分、积分参数。G0（s）为简化的纵向传递函数，在建模时采用小扰动纵向线性模型［2］，忽略了控制舵的动态特性，开环仿真结果如图2所示，与试验和CFD结果吻合较好。根据经典控制理论设计了控制律

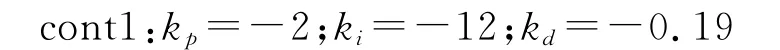
单位阶跃响应曲线如图4所示，上升时间0.06s，调节时间0.48s，超调量13%，动态响应较好。

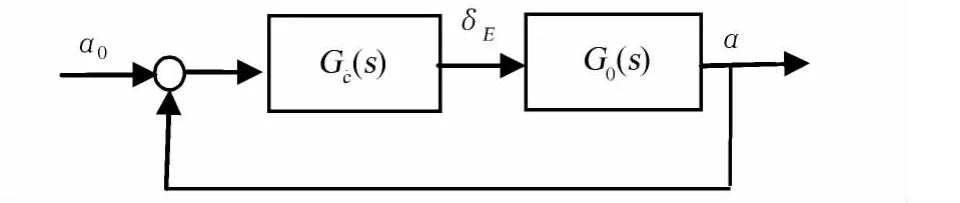
图3 迎角PID控制结构Fig.3 Structure of PID control for angle of attack

图4 PID控制阶跃响应Fig.4 Step response of PID control

2.2 配平飞行数值模拟

一般认为，阶跃输入对系统是最严峻的工作状态，如果阶跃输入作用下的动态性能满足要求，那么系统在其它形式的输入作用下，其动态性能也是满意的。就迎角从0°拉起到5°，进行闭环PID控制数值模拟。计算Ma＝0.6，图5是迎角时间历程和舵偏角时间历程，虽然上升时间很快，但是超调量超过了50%，且振荡严重。

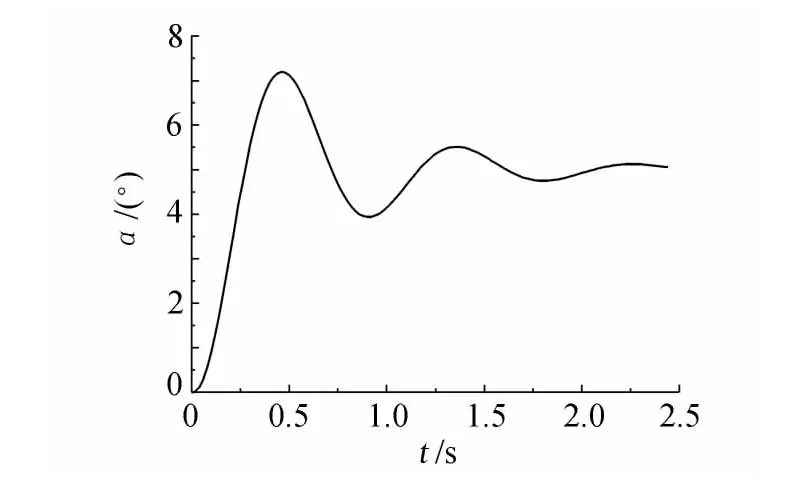
图5 PID控制CFD模拟结果Fig.5 CFD Simulation Result of PID Control

3 控制参数优化

在经典控制理论中，很多情况下由理论设计的控制参数并不最优，为了寻求更好的控制效果，往往要不断调整参数，并通过试验确定。对导弹来说，通常由试飞来检验控制系统，这是昂贵、费时和危险的方法［7，16］。数值模拟技术则不存在这些问题。针对超调量过大、振荡剧烈的问题，通过数值模拟对参数进行优化改进。根据PID三个参数对动态响应的影响特性，依次设计了6组参数，分别如下：

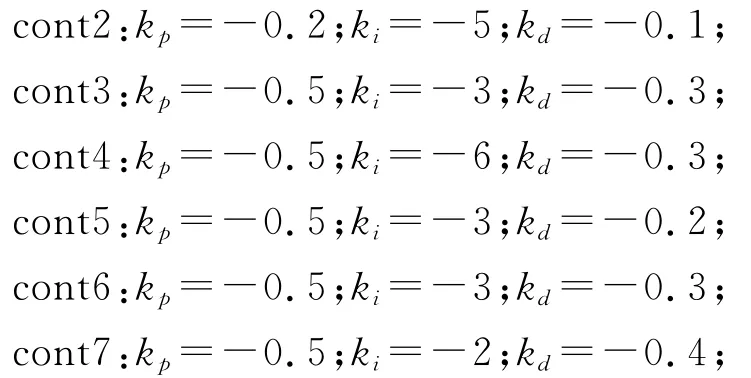
模拟结果如图6，动态性能指标［17］列于表1。从结果看，cont1的超调量最大，但是它的前3个时间指标都较好。cont5的超调量最小，调节时间也最短，只有1.18s，优于cont1的1.7s，上升时间0.34s，满足导弹动态响应指标要求。从迎角曲线看出，在经历第一次超调后，没有发生振荡，直接稳定到了5°，最终配平舵偏角－2.37°。总的来看，cont5具有不错的动态性能。cont5的俯仰力矩时间历程（图7）也表明力矩趋于0。

图6 迎角时间历程比较Fig.6 Compare of time history for angle of attack

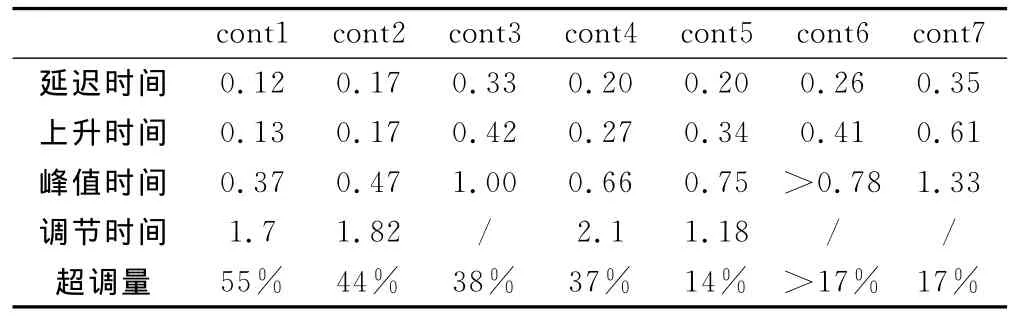
表1 各控制器动态性能指标Table1 Dynamic performance for each aontroller

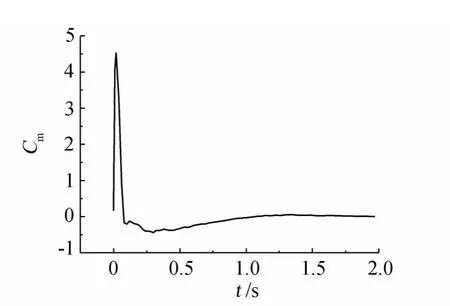
图7 控制器5俯仰力矩系数时间历程Fig.7 Time history of pitching moment coefficient for controller 5

图8是使用cont5参数进行阶跃响应的仿真结果，以及在图6中cont5舵偏控制下的响应仿真结果，它们与数值模拟迎角曲线都有较大差异。图6清晰地表明舵偏角在控制初段迅速变化，最大角速度达到了200°／s。图2所示开环算例的舵偏角速度只有6.7°／s，是准静态问题，所以仿真结果与CFD计算结果吻合较好。而当实际控制时，很大的舵偏速度引入了更强的非定常效应，此时简化数学模型便不能精确描述这些过程，从而导致了仿真结果与模拟结果的差异。

图8 单位阶跃和受控响应（cont5）Fig.8 Step and control responses of PID controller 5

4 结 论

（1）使用双时间步三阶Adams预估校正法耦合空气动力学／飞行力学计算，模拟了纵向开环虚拟飞行，与试验和仿真结果一致性较好，表明计算方法可以用于此条件下气动／运动／控制一体化数值模拟；

（2）通过对导弹配平飞行数值模拟，检验和改进了PID参数，超调量从超过50%降低到14%，调节时间从1.7s降低到1.18s，上升时间0.34s，满足动态性能要求；

（3）要使仿真结果更准确、可靠，必须在数学模型中充分考虑各种非定常效应，并对控制律进行仔细设计，这往往是比较困难的；

4 发展的虚拟飞行数值模拟技术能反映动态过程，是检验和优化控制方法的有效途径，具有应用潜力。

［1］STEVENS B L，LEWIS F L.Aircraft simulation and control［M］.John Wiley and Sons Inc，1992.

［2］YANG J，ZHANG X F，YUAN B，et al.Missile control theory［M］.Beijing：National Defense Industry Press，2008.（in Chinese）杨军，张晓峰，袁博，等.导弹控制原理［M］.北京：国防工业出版社，2008

［3］ALLWINE D A，STRAHLER J A，LAWRENCE D A，et al.Nonlinear modeling of unsteady aerodynamics at high angle of attack［R］.AIAA 2004－5275

［4］PHILLIPS W H.Flying qualities from early airplanes to the space shuttle［R］.AIAA 88－0751，1988

［5］TAO Yang，FAN Zhaolin，WU Jifei.CFD based virtual flight simulation of square cross－section missile with control in longitudinal flight［J］.Chinese Journal of Theoretical and Applied Mechanics，2010（2）：169－176.（in Chinese）陶洋，范召林，吴继飞.基于CFD的方形截面导弹纵向虚拟飞行模拟［J］.力学学报，2010（2）：169－176.

［6］ALLAN M R，BADCOCK K J，RICHARDS B E.CFD simulation of longitudinal flight mechanics with control［R］.AIAA 2005－46

［7］SALAS M D.Digital flight：the last CFD aeronautical grand challenge［J］.Journal of Scientific Computing，2006，28（213）：479－505.

［8］HALL L H，PARTHASARATHY V.Validation of an automated chimera 6－dof methodology for multiple mov－ing body problems R.AIAA Paper 9816574

［9］NICHOLS R H，DENNY A G.Numerical simulation of a store in controlled separation［R］.AIAA9933437

［10］HALL L H，MITCHELL C R，PARTHASARATHY V.An unsteady simulation technique for missile guidance and control applications［R］.AIAA Paper 9715666

［11］SAHU J.Coupled CFD and rigid body dynamics modeling of a spinning body with flow control［R］.AIAA－2004－2317，2004

［12］SØRENSEN K A，TREMEL U，RIEGER H，et al.Simulation of manoeuvring aircraft with the unstructured chimera approach［R］.AIAA－2007－123

［13］DA X Y，TAO Y，ZHAO Z L.Research on virtual flight simulation based on prediction－correction coupling method and chimera grid［J］.Acta Aeronautica et Astronautica Sinica，2012，33（6）：977－983（in chinese）达兴亚，陶洋，赵忠良.基于预估校正和嵌套网格的虚拟飞行数值模拟［J］.航空学报，2012，33（6）：977－983.

［14］TAO Y，YUAN X X，FAN Z L，et al.Numerical investigation of dynamic behavior of square section missile in roll at high incidence［J］.ACTA Aerodynamica Sinica，2010，28（3）：285－290（in chinese）陶洋，袁先旭，范召林，等.方形截面导弹摇滚特性数值研究［J］.空气动力学学报，2010，28（3）：285－290.

［15］DA X Y，TAO Y，ZHAO Z L.Virtual flight Navier－Stokes solver and its application［J］.Procedia Engineering，2012，31：75－79.

［16］LAWRENCE F C，MILLS H.Status update of the AEDC wind tunnel virtual flight testing development program［R］.AIAA Paper 2002－0168，2002

［17］HU S S.Automatic control theory［M］.Beijing：Science Press，2007.（in Chinese）胡寿松.自动控制原理［M］.北京：科学出版社，2007.