细长三角翼滚转/侧滑耦合运动效应分析
杨小亮,刘伟,吴天佐,刘绪
(国防科学技术大学航天科学与工程学院宇航科学与工程系,湖南 长沙 410073)
0 引言
滚转/侧滑双自由度耦合运动如图1所示,战斗机在绕体轴发生摇滚的同时,质心左右移动。这种耦合运动形式与荷兰滚(Dutch Roll)现象有一定的相似之处:从后面看战斗机就像钟摆左右摆动,从上面看战斗机沿蛇行路线前进,但滚转/侧滑双自由度耦合的摇滚运动比荷兰滚更为复杂。荷兰滚是横侧小扰动模态[1],可采用线性气动模型描述,而摇滚是大迎角下的非线性气动现象,必须采用非线性的气动模型进行研究。
研究多自由度耦合的运动特性具有实际意义,贾区耀[2-3]在对飞行器大气自由飞的结果和风洞实验数据进行对比分析时就发现,风洞实验或数值计算表明是稳定的某些飞行器,自由飞的结果却是不稳定的,分析认为自由度不相似可能是导致这些差异的重要原因之一。事实上,真实飞行条件下,摇滚现象通常是多自由度耦合的运动,因此,根据飞行器运动的特点,分析并满足主要的自由度相似,研究多自由度耦合的翼摇滚特性是非常必要的。
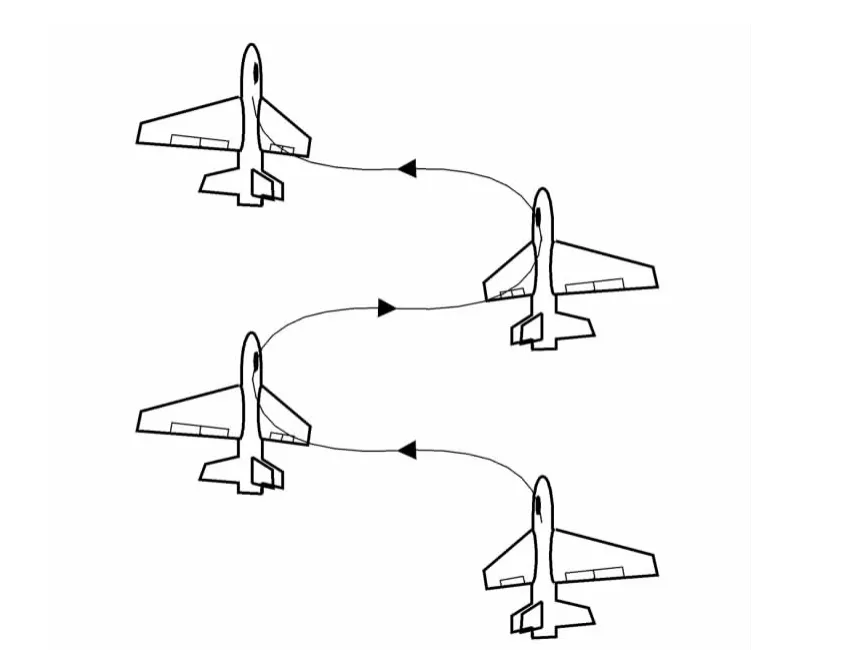
图1 飞行器滚转/侧滑耦合运动示意图Fig.1 Schematic of aerocraft in combined free roll and free sideslip motion
三角翼结构简单、流场中有丰富的涡结构,被认为是动态特性研究最理想的对象之一,国内外涌现了大量针对三角翼开展的动态实验和数值模拟研究,也取得了重要的进展。通过分析发现,这些研究主要针对三角翼单自由度俯仰或滚转的运动特性,仅有少量文献涉及了多自由度耦合运动,文献[4-5]研究三角翼俯仰/滚转耦合运动特性,文献[6]则对三角翼滚转/侧滑耦合运动进行探索,可见对多自由度耦合运动特性的研究还很不充分。另外,文献[7-8]采用纯强迫运动研究三角翼的耦合运动,虽然能够从一定程度反映三角翼气动力/力矩的迟滞特性,但对纵横向运动交感耦合特性的模拟有其无法回避的局限性。
除滚转自由度外,摇滚过程中的侧力,可导致战斗机在摇滚同时发生侧滑运动,因此,侧滑也是主要自由度之一。本文数值模拟尖锐前缘的80°后掠平板三角翼自由滚转、自由侧滑双自由度耦合的运动特性,并与单自由度翼摇滚比较,分析三角翼滚转/侧滑耦合的运动机制,研究耦合运动过程中的耦合效应及其流场特性。
1 研究方法
数值模拟研究细长三角翼自由滚转、自由侧滑的耦合运动,需要建立滚转/侧滑双自由度耦合运动的模型,采用合理的数值方法离散控制方程组,然后生成计算网格数值模拟三角翼非定常的动态运动过程。
1.1 滚转/侧滑双自由度耦合运动模型
本文研究的双自由度运动涉及自由滚转和自由侧滑,将转动运动方程建立在体坐标系下可以保持三角翼转动惯量为常量,将质心运动方程建立在惯性坐标系中便于描述三角翼质心的运动。三角翼耦合运动的无量纲控制方程组可写为:

式中Ek和Evk分别为对流通量和粘性通量,φ和z分别为滚转角和惯性系下质心Z坐标,Cl和Cz分别为滚转力矩系数和侧向力系数,无量纲转动惯量Ixx和无量纲质量m分别为:
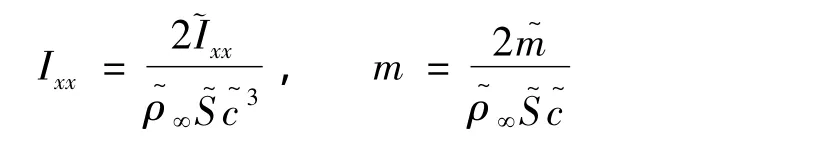
带上标“~”表示有量纲量,式中S~和 c~分别表示参考面积和参考长度。由此建立了三角翼自由滚转、自由侧滑双自由度耦合的动力学方程组,采用无量纲化的NS方程组作为流动控制方程组,则构成对三角翼滚转/侧滑双自由度运动的完整描述,可应用适当的数值方法进行离散求解。
1.2 数值方法
采用二阶迎风型NND格式[6]有限体积离散流动控制方程组的空间导数项,采用含双时间步的LUSGS方法[7]来提高时间求解的效率和精度。三角翼背风面的流动具有典型的湍流特征,引入基于工程经验和量纲分析的SA模型[8]模拟三角翼上多涡流结构的湍流效应。
刚体动力学方程组采用二阶精度的单边差分离散求解,流动控制方程组和刚体动力学方程组采用松耦合算法求解。
计算时,远场边界的处理采用基于Riemann不变量、适用于动态运动的无反射边界条件[9]。壁面边界,速度采用无滑移条件,温度采用绝热壁条件,压力条件计入离心力的影响。
1.3 三角翼模型及网格
计算采用80°后掠的三角翼模型,前缘及尾缘采用向下削尖处理。对于这类具有尖锐前缘的外形,生成OH型的计算网格能够较好平衡模拟精度和网格规模[10]。本文采用的计算网格整体情况如图2所示,网格大小为73×77×47,对应流向、周向和法向,网格上游边界距离三角翼的顶点3倍根弦长度,周向边界分别距离体轴3倍根弦长度,下游边界距离三角翼的尾缘5倍根弦长度。截面网格采用O型拓扑结构,壁面第一层网格法向尺度控制为5×10-5倍根弦长度,利用Laplace方程作适当正交优化。
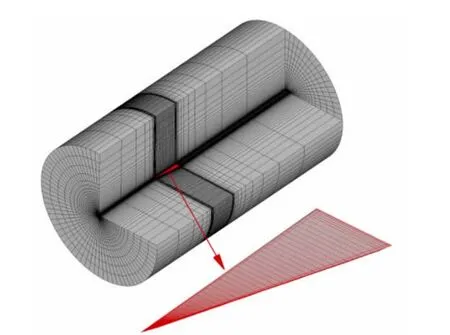
图2 80°后掠三角翼模型及空间网格分布Fig.2 The 80°swept delta wing model and space computational grid distribution
2 结果及分析
2.1 三角翼滚转/侧滑耦合摇滚特性及与单自由度摇滚特性的比较
首先数值模拟三角翼的单自由度自激摇滚特性,作为对程序的考核,并用于与三角翼双自由度耦合摇滚运动特性的比较,研究侧滑自由度对摇滚特性的影响。采用来流马赫数Ma=0.35,基于根弦长度的雷诺数Re=2.5×106,三角翼绕体轴的无量纲转动惯量Ixx=0.0622,给定30°名义迎角和0°初始滚转角,三角翼单自由度摇滚特性如图3所示。三角翼摇滚振幅逐渐增大,经过10个周期的发展,形成频率稳定的、极限环形式的、振幅约为37.7°的自维持等幅振荡。图3(b)所示的摇滚相曲线显示三角翼的摇滚逐渐收敛到极限环形式的周期吸引子形态。国内外实验和数值模拟研究表明,细长三角翼单自由度摇滚表现为极限环形式的周期性等幅振荡,由于模型加工、支架安装以及轴承摩擦等因素的影响,这些结果之间存在着一定的差异。本文模拟得到三角翼单自由度自激滚转的振幅约 37.7°,与实验[11]和数值模拟[9]结果(振幅在30°~40°)能够较好的吻合。

图3 滚转/侧滑耦合运动与单自由度自激摇滚运动特性的比较Fig.3 The comparison of characteristics between combined roll and sideslip motion and wing rock
研究滚转/侧滑耦合的双自由度运动涉及三角翼的转动和平动,除转动惯量外,还应指定三角翼的质量。采用与单自由度相同的计算条件,并指定三角翼的无量纲质量m=25.0,模拟80°后掠三角翼滚转/侧滑的双自由度耦合运动,结果如图3所示。同时允许自由滚转、自由侧滑条件下,三角翼从0°滚转角位置开始,滚转振幅逐渐增大,经过约9个周期的发展,形成振幅和频率稳定的周期性等幅摇滚振荡。在本文条件下,三角翼滚转/侧滑耦合运动的摇滚振幅约为51.5°,如图3(a)所示,显著大于单自由度自激摇滚时37.7°的振幅,双自由度条件下滚转运动的频率较低、周期较长,虽然二者达到极限环形式的周期性振荡所经历的周期数不同,但所历经的时间大致相同,图中位置A所示。图3(b)所示的相曲线上可以看到,在侧滑自由度的影响下,三角翼滚转运动的相曲线仍收敛到极限环形式的周期吸引子形态,在本文的质量和转动惯量条件下,双自由度耦合运动的极限环显著大于单自由度摇滚的极限环,也就是说:在相同的滚转角下,双自由度条件下的滚转角速度更大;在达到相同的角速度时,双自由度条件下的三角翼所达到的滚转角更大。
随着市场经济体制的发展以及与之相匹配的法律法规的完善,现代社会为个体追求和实现自我利益提供了相对公平的场域。 任何个人、团体都可以作为市场主体参与市场竞争,并以此实现自身的合法利益。 “为我”的利益诉求日益为更多的个体所认可,利益主体迅速多元化,市场成为“各种利益主体不断角逐的活动过程”[2]。 在这一过程中,个体与个体之间,个体与社会群体之间、群体与群体之间的利益矛盾此消彼长、盘根错节。
滚转/侧滑耦合运动的摇滚振幅与质量有关,进一步的计算表明,随着质量增大,滚转/侧滑耦合的摇滚振幅有所减小,但三角翼滚转/侧滑双自由度耦合条件下的摇滚振幅均大于单自由度摇滚的振幅。当质量特别大时(比如m=1000.0),滚转/侧滑耦合运动的摇滚特性和单自由度摇滚的特性接近。
2.2 滚转/侧滑耦合运动的流场特性
为研究三角翼滚转/侧滑耦合运动时的流动机理,选择极限环振幅建立后的一个滚转“正”行程(ωx>0)绘制截面流场,分析三角翼背风面的非定常流动特性。图4是滚转“正”行程x/c=0.67截面流向涡量Ωx随滚转角的演化,显示前缘集中涡在翼面上的非对称发展过程。虚线表示流向涡量Ωx<0,实线表示流向涡量Ωx>0。按照滚转角的变化,该过程大致分为三个阶段:
第一阶段,图4(a~d),三角翼具有负滚转角,翼面右侧前缘产生的集中涡占主导,形成正的滚转力矩,使三角翼滚转角速率增大。右侧翼面上除了主翼涡外,还有结构清晰的二次分离结构。随着三角翼的滚转,两侧涡非对称增长,左侧涡迅速增强,右侧涡缓慢增长,由非对称造成的滚转力矩逐渐减小,因此,虽然三角翼滚转的角速率持续增大,但角加速率越来越小。
第二阶段,图4(e),此时三角翼位于0°滚转角附近,由于滚转导致的迟滞效应,右侧涡较为贴近翼面,结构较为紧凑,翼面两侧涡强度大致相当,使三角翼滚转的力矩显著减小,滚转的角速率接近极值。此时,由于左侧涡显著增强,其正下方靠近前缘的位置开始形成二次涡。

图4 滚转正行程(ωx>0)截面(x/c=0.67)流向涡量Ωx的演化Fig.4 The evolution of sectional(x/c=0.67)streamwise vorticity in positive rolling procession
第三阶段,图4(f~i),这一阶段三角翼具有显著的正滚转角,翼面左侧前缘产生的集中涡占主导,形成负的滚转力矩,使三角翼的滚转减速。在0°滚转角位置附近,图4(e),翼面两侧的主涡强度相当,随着三角翼左滚,背风面左右两侧的主涡非对称减弱,左侧涡强度缓慢减弱但更加靠近翼面,右侧涡强度迅速衰减且远离翼面,翼面两侧涡结构非对称逐渐加剧,形成负的滚转力矩,使得三角翼滚转速率减小。
在第三阶段滚转减速的过程中,二次涡的发展与第一阶段滚转加速的过程不同。由于涡结构随滚转运动的迟滞特性:抬起一侧翼面上二次涡区域随着滚转减速逐渐缩小,直至25.5°滚转角时,图4(g)中右侧仍有显著的二次涡区域,而在滚转加速时,图4(c)中左侧翼面上这一特征不明显;下沉一侧翼面上二次涡区域随着滚转减速逐渐扩大,至最大滚转角51.5°时达到最大,图4(i)中左侧,而在滚转加速的过程中,下沉一侧二次涡区域的范围变化较小,图4(a~d)中右侧。由此可见,滚转动态迟滞特性使得涡结构在滚转加速和减速过程中的发展具有不同的特征。
图4显示在最大滚转角位置,滚转角速度为零,侧滑速度也趋于零。在负滚转角时,图4(a~d),三角翼背风面的外法向偏向图中右侧,法向力是沿外法线方向的,因此法向力的侧向分量也指向图中右侧,将使得三角翼向右的侧滑加速;滚转角回到0°滚转角位置时,图4(e),集中涡产生的法向力指向翼面上方,侧向作用面积较小,没有显著的侧向分量,三角翼以较大的速度继续向右侧滑运动;在正的滚转角时,图4(f~i),上翼面前缘集中涡转到左侧,前缘集中涡产生的吸力区将产生向左的侧力,使得向右的侧滑减速,当达到最大滚转角时,图4(i),右侧滑速度趋于零。三角翼的右侧滑停止以后,集中涡引起向左的侧力,使得三角翼开始左侧滑的加速,进入侧滑运动的“正”行程,如此往复形成三角翼的侧滑振荡。
2.3 滚转/侧滑双自由度耦合运动机制分析
正如翼摇滚命名所指,滚转是最主要的自由度。导致三角翼侧滑运动的侧力源于法向力在侧向的分量,伴随三角翼滚转运动所产生,与滚转角的方向密切相关,因此三角翼侧滑运动的频率特性主要与滚转运动相似。图5是滚转/侧滑双自由度耦合运动时滚转角速度和侧滑速度随时间变化的曲线,如图所示,二者几乎是同频率、反相位的关系。
依据2.2节对三角翼上涡流演化特性的分析以及图5所示的运动学关系,可分析三角翼的双自由度耦合运动机制。图6是三角翼滚转/侧滑耦合运动的示意图,采用飞行视角绘制,即从三角翼尾缘向顶点方向观察,图中弯转细实线箭头表示滚转方向,水平粗虚线箭头表示侧滑速度方向。
在滚转运动的“正”行程(ωx>0,即左滚:左侧翼面下沉,右侧翼面上升,图中①~⑤号位置),位置①三角翼具有最大的负滚转角,滚转角速度和侧滑速度都接近零,三角翼左右两侧翼面上涡流结构的非对称形成正的滚转力矩,使得三角翼左滚加速,负的滚转角导致法向力存在向右的分量,三角翼向右侧滑并加速,运动到位置②,形成左滚右侧滑的运动;正的滚转力矩和法向力向右的分量使得三角翼的左滚和右侧滑进一步加速,到达位置③,这时左滚角速度和右侧滑速度都接近极值(由于迟滞特性,左滚可能还会继续加速,不完全等于极值),形成滚转“正”行程中最显著的左滚右侧滑运动;位置④,由于翼面两侧涡流位置和强度的非对称状况发生改变,形成负滚转力矩使三角翼左滚减速,此外正滚转角引起法向力向左的分量,使三角翼右侧滑运动也减速,但仍保持左滚右侧滑的运动状态;随着左滚和右侧滑运动的进一步减速,运动到达位置⑤,三角翼左滚角速度和右侧滑速度减小到零,三角翼左滚右侧滑的过程终止。

图5 侧滑速度和滚转角速度时间历程曲线Fig.5 The time history curves of sideslip velocity and roll angular velocity

图6 三角翼滚转/侧滑耦合运动机制示意图Fig.6 Schematic of the kinematic coupling mechanism of combined free roll and free sideslip motion
滚转运动的“负”行程(ωx<0,右滚:右侧翼面下沉,左侧翼面上升,图中⑤~⑨号位置),与“正”行程的情况相反,以正行程终止的位置⑤为起始位置,该位置具有最大的正滚转角,滚转角速度和侧滑速度都接近零,翼面上非对称涡流结构产生负的滚转力矩,使三角翼进入右滚,正滚转角引起法向力向左的分量,三角翼开始左侧滑加速,到达图中位置⑥,形成右滚左侧滑的运动;负的滚转力矩和法向力向左的分量使得三角翼的右滚和左侧滑进一步加速,到达位置⑦,此时左滚角速度和右侧滑速度接近极值,形成“负”行程最显著的右滚左侧滑运动;到位置⑧,翼面两侧涡的位置和强度的非对称状况发生改变,正滚转力矩使得三角翼右滚减速,正滚转角引起向左的法向力分量,三角翼左侧滑减速,但仍保持右滚左侧滑的运动状态;随着右滚和左侧滑运动进一步减速,运动到达位置⑨,三角翼右滚角速度和左侧滑速度减小到零,三角翼右滚左侧滑的过程终止。位置⑨和位置①的情况相同,三角翼又进入左滚右侧滑,往复形成三角翼滚转/侧滑双自由度耦合的运动。
综上所述,三角翼滚转/侧滑双自由度的耦合运动机制可以描述为:飞行视角下左滚右侧滑,右滚左侧滑的耦合运动。
2.4 滚转/侧滑运动的耦合效应分析
可以证明,三角翼单自由度摇滚的迎角和侧滑角与滚转角有如下关系:
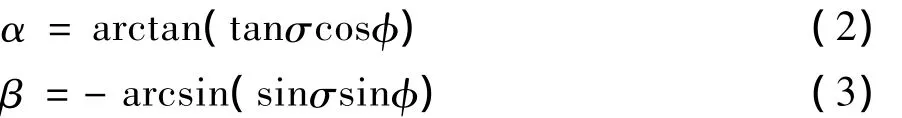
名义迎角σ为根弦与来流的夹角,等于初始时刻的迎角。由此可知单自由度条件下,σ不变时,迎角和侧滑角与滚转角一一对应。
然而滚转/侧滑耦合的运动,迎角和侧滑角还受到无量纲侧滑速度w0的影响,可以证明滚转/侧滑双自由度耦合运动条件下,迎角和侧滑角有如下表达式:
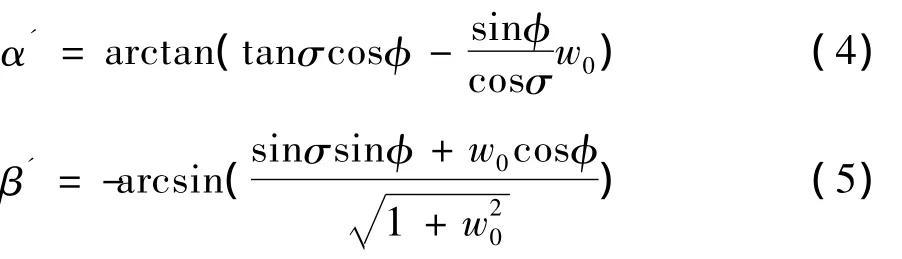
由图5可知,滚转/侧滑耦合运动下,侧滑运动并不剧烈,侧滑速度比来流速度小两个量级,可以作为小量处理,因此式可以简化为:

对比(6)式和(3)式,可求得侧滑运动引起的侧滑角增量dβ=β'-β表示为:
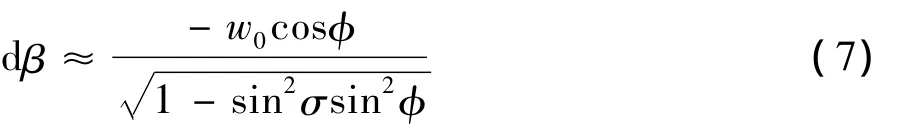
根据上式可知,侧滑运动引起侧滑角的增量与侧滑速度符号相反,也就是说正的侧滑速度引起侧滑角减小,负的侧滑速度引起侧滑角增大。绘制侧滑角随滚转角的变化,如图7(a)所示,图中实线为单自由度翼摇滚的侧滑角,点划线为滚转/侧滑耦合运动的侧滑角。在滚转运动的正行程,侧滑运动导致三角翼的侧滑角增大,在滚转运动的负行程,侧滑运动使得三角翼的侧滑角减小,说明侧滑运动导致了侧滑角在摇滚过程中的迟滞效应,由2.2节的分析知,侧滑速度与滚转角速度反相,图示的滞后效应与分析相符。图7(b)是侧滑运动引起的侧滑角增量随滚转角的变化,曲线以顺时针的螺旋线收敛到一个“菱形化的圆”,表明周期性的耦合摇滚形成以后,侧滑运动将固定地在滚转运动的正、负行程分别引起侧滑角增大和减小。
同理可得,侧滑运动引起迎角的增量为:

侧滑速度与滚转角速度反相,则三角翼在滚转运动的正负行程经过同一滚转角位置的侧滑速度相反,由上式可知将引起符号相反的迎角增量,如图8所示。可见,侧滑运动的引入导致了迎角随滚转角的变化也产生了迟滞效应,加速滚转的过程,侧滑运动使得迎角减小,减速滚转的过程,侧滑运动使得迎角增大。

图7 三角翼滚转/侧滑耦合运动对侧滑角的影响Fig.7 Influence of the coupling effects in combined roll and sideslip motion on sideslip angle
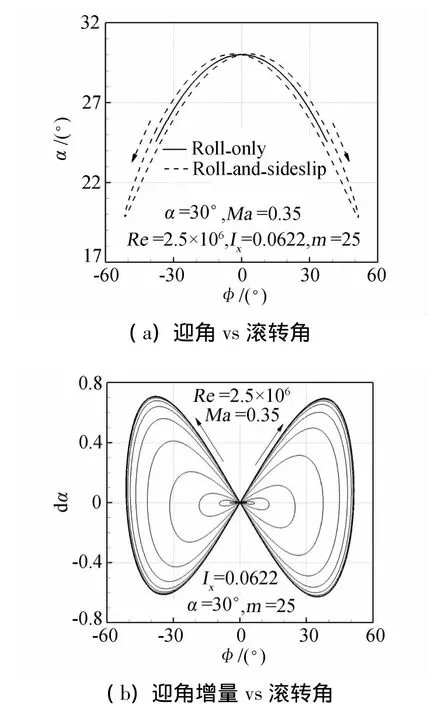
图8 三角翼滚转/侧滑耦合运动对迎角的影响Fig.8 Influence of the coupling effects in combined roll and sideslip motion on attack angle
3 结论
(1)三角翼自由滚转/自由侧滑双自由度耦合的摇滚运动比单自由度翼摇滚复杂,振荡更剧烈:相同的滚转角时,双自由度耦合运动的滚转角速度更大;在达到相同的角速度时,滚转/侧滑耦合条件下的三角翼所达到的滚转角更大。
(2)滚转/侧滑双自由度耦合运动条件下,涡流的非对称迟滞特性仍是维持三角翼摇滚的流动机理;侧滑运动强化了涡流的迟滞特性,引起迎角和侧滑角随滚转角迟滞变化,从而加剧三角翼上涡流的非对称变化,可能导致滚转/侧滑双自由度耦合的摇滚更为剧烈。
(3)三角翼滚转/侧滑耦合的运动,滚转是主要的自由度,侧滑速度与滚转角速度同频率、反相位,左滚右侧滑和右滚左侧滑是三角翼滚转/侧滑双自由度耦合运动的作动机制。
[1]胡兆丰,何植岱,高浩.飞行力学——飞机的稳定性和操纵性[M].国防工业出版社,1985.
[2]贾区耀.天空飞行与地面风洞实验动态气动相关性研究[J].实验流体力学,2006,20(4):87-93.
[3]贾区耀,杨益农,陈农,天空飞行与地面风洞实验动态气动相关中的雷诺数影响[J].实验流体力学,2007,21(4):91-96.
[4]唐敏中,张伟,何宏丽.俯仰-滚摆耦合复杂流场试验研究[J].空气动力学学报,2001,19(1):47-55.
[5]杨小亮,刘伟,赵云飞,刘君.80°后掠三角翼强迫俯仰、自由滚转双自由度耦合运动特性数值研究[J].空气动力学学报,2011,29(4):421-426.
[6]杨云军,崔尔杰,周伟江.细长三角翼滚转/侧滑耦合运动的数值研究[J].航空学报,2007,28(1):14-19.
[7]KANDIL O A,MENZIES M A.Coupled rolling and pitching oscillation effects on transonic shock-induced vortex-breakdown flow of a delta wing[R].AIAA96-0828,1996.
[8]郭迪龙,杨国伟,康宏琳,王发民.三角翼受迫俯仰滚转耦合运动的气动特性研究[J].空气动力学学报,2007,25(1):65-69.
[9]SHEN Q,ZHANG H X.A new upwind NND scheme for Euler equations and Its application to the supersonic flow[A].The Proceedings of ASIA Workshop on CFD[C].Sichuan,China,1994.
[10]JAMESON A.Time dependent calculations using multigrid with application to unsteady flows past airfoils and wings[R].AIAA 91-1596,1991.
[11]SPALART P R,ALLMARAS S R.A one-equatlon turbulence model for aerodynamic flows[R].AIAA 92-0439,1992.
[12]刘伟.细长机翼摇滚机理的非线性动力学分析及数值模拟方法研究[D].[博士学位论文].长沙:国防科学技术大学,2004.
[13]刘刚,周铸,黄勇,等.三角翼大迎角绕流数值模拟中网格的影响研究[J].空气动力学学报,2004,22(4):481-485.
[14]NGUYEN L E,YIN L P,CHAMBERS J R.Self-induced wing rock of slender wings[R].AIAA paper 81-1883,1981.

