基于性能及轻量化的新型风力机叶片优化设计研究
汪 泉,陈 进,郭小峰,李松林,王旭东
(1.重庆大学机械传动国家重点实验室,重庆 400030;2.湖北工业大学机械工程学院,湖北 武汉 430068;3.重庆工商大学机械工程学院,重庆 400067)
0 引 言
随着风力机风轮直径的增加,准确的预测其能量输出及气动载荷特性变得越来越重要。对于提高风力机风轮功率系数,常见的方法是应用不同的翼型、改变叶片的弦长与扭角分布、进行失速控制及俯仰控制等等。
对于风力机叶片设计研究,Kamoun Badreddinne[1]以风力机输出功率为优化目标,对叶片的升力变化过程进行了研究,并将此与Glauert模型进行了对比,然后对叶片进行了优化设计;汕头大学刘雄[2]等考虑了风场风速的概率分布,以风力机年能量输出最大为优化目标,使用遗传算法,优化得到了1.3MW风力机叶片;华北电力大学韩中合等[3]提出了多次迭代优化设定诱导因子初始值的方法,以功率输出和年发电量最大为优化目标,对1.5MW风力机叶片进行了优化设计;重庆大学 Wang Xudong[4]以风力机单位发电量的成本为目标,对几种不同装机容量的风轮进行了优化设计,降低了风力机单位发电量的成本。此外,还有一些学者对此做了很多研究[5-10],都值得借鉴参考。
然而以上研究大都针对现有叶片进行改进,很少有对具有全新翼型族的叶片进行优化设计,而且在对叶片外形的优化过程中忽略了减少叶片质量对提高风力机叶片疲劳寿命及降低叶片材料成本这一至关重要的因素。而风力机叶片是由复合材料加工制造而成,叶片密度变化不一,其曲面形状非常复杂,采用传统的复合材料层合板理论很难建立叶片的质量计算数学模型,因此,在其他条件一致的情况下(叶片铺层厚度、密度等),本文提出将叶片的质量计算转化为叶片曲面面积的计算模型,要使质量最小,意味着对应的曲面面积最小。在整个变桨距风力机叶片设计上,采用作者全新设计的CQU-A翼型族,验证该翼型族具有较高的气动性能。基于修正的风力机空气动力学模型理论,并提出以最大功率系数及最小叶片面积为多目标优化模型,以弦长和扭角为设计参数,考虑叶根载荷约束,采用改进的多目标粒子群算法对2MW风力机叶片进行设计与优化,并将优化结果与初始叶片以及欧盟Tjære实验叶片进行对比分析,以验证该优化设计方法的可行性及优越性。
1 修正的风轮空气动力学模型
一维动量理论对风轮进行空气动力特性分析的前提是假设风轮由无限个叶片组成,而事实上风轮都是由有限叶片来组成的。这样使得这两种模型的风力机尾流中的旋涡系不同。普朗特给出了叶尖修正因子F,推导出风轮的推力与扭矩为[11]:
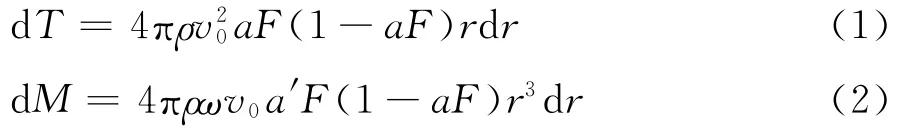
ρ ——空气密度;
v0——来流风速;
a——轴向诱导因子;
F——普朗特叶尖损失修正因子;
r——叶片展向位置;
ω——风轮转动角速度;
a′——周向诱导因子;
φ——入流角;
B——叶片个数;
R——风轮半径;
普朗特叶尖修正模型主要针对轴向质量流量进行了修正,Shen修正模型对风轮叶素中的法向力系数和切向力系数做了进一步的修正[12],引入修正因子F1并代入经典的叶素理论中得到推力与转矩为:

g=exp[-0.125(Bλ-21)]+0.1
vrel——入流相对风速;
c ——叶片弦长;
λ ——叶尖速比;
Cn——法向力系数;
Ct——切向力系数;
联立(1)~(4)可以求出轴向诱导因子a和周向诱导因子a′为:

式中 Y1=4F sin2φ/(σCnF1)
Y2=4F sinφcosφ/(σCtF1)
σ=Bc/(2πr)
当轴向诱导因子a>0.3时,叶素理论将不再准确可靠,此时就需要对风力机的推力进行修正。那么轴向诱导因子a和周向诱导因子a′为

式中ac=1/3。
2 叶片设计及优化模型的建立
2.1 新型风力机叶片设计
本研究在整个叶片上全部采用作者新设计的CQU-A翼型系列(相对厚度从15%~40%的七种翼型,如图1、图2)高性能风力机专用翼型,该翼型系列基于广义泛函及儒科夫斯基保角变换的理论设计方法。该方法将近似于圆的图形通过儒科夫斯基保角变换生成翼型,改变其控制方程中的系数就能够控制翼型型线,通过这种方法,已优化出性能较好的翼型[13-14]。

图1 CQU-A翼型系列Fig.1 CQU-A airfoil series
为了验证CQU-A翼型系列具有较高的气动性能,选取叶片主要产生功率区域的两种翼型CQUA180及CQU-A210与相当厚度的DU翼型进行对比分析。采用RFOIL软件计算翼型的气动性能。其中以自由转捩工况模拟光滑条件;以固定转捩工况模拟粗糙条件,转捩模型采用吸力面(上翼面)处于1%弦长位置固定转捩,压力面(下翼面)处于10%弦长位置固定转捩[15]。图 3为 CQU-A180翼型与DU96-W-180翼型在相同运行工况下(Re=3×10 Ma=0.15)的气动特性对比图。从图中可以看出,无论是光滑条件,还是粗糙条件下,新翼型的升力系数、升阻比均有显著的提高。图4为CQU-A210翼型与DU93-W-210翼型在相同工况下的气动性能对比图。在翼型失速之前,新翼型的最大升力系数、最大升阻比均有较大提高。表1给出了四种翼型的气动特性数据对比,结合图表,表明新设计的翼型无论是在光滑条件还是粗糙条件,均具有高的升力系数和升阻比。

图2 CQU-A翼型系列Fig.2 CQU-A airfoil series

图3 CQU-A180翼型与DU96-W-180翼型气动性能对比Fig.3 The comparison of aerodynamic performance of CQU-A180airfoil and DU96-W-180airfoil

图4 CQU-A210翼型与DU93-W-210翼型气动性能对比Fig.4 The comparison of aerodynamic performance of CQU-A180airfoil and DU93-W-210airfoil

表1 翼型气动性能参数对比Tbale 1 The comparison of aerodynamic performance of airfoils
风力机叶片设计的基本参数如表2所示。其中各个翼型按照对应于2MW叶片展向位置处的气动条件进行设计,根据额定运行工况条件下,翼型所处展向位置处的弦长及相对来流速度确定雷诺数和马赫数。翼型沿叶片展向布置及边界层条件见表3所示,其中相邻翼型间的过渡翼型,通过相邻翼型的坐标插值得到。由于翼型沿叶片展向分布时其雷诺数会不一样,表3中给出了当叶片旋转速度为20rpm时几个关键叶片段的雷诺数大小,由于马赫数对叶片翼型的气动性能影响不大,因此这里取整个叶片的马赫数为0.15。

表2 叶片设计基本参数Table 2 The basic parameter of the designed blade

表3 翼型沿叶片展向分布及边界层条件Table 3 The airfoils along the blade span-wise distribution and the boundary layer conditions
2.2 建立多目标优化模型
2.2.1 目标函数
对于变桨距风力机而言,风轮转速可以连续进行调节,就有可能使风力机运行在最优点Cp,max,因此本文以风力机功率系数最大作为目标优化之一:

基于风力机功率系数的定义,我们可以得到以下表达式:

按照修正的叶素动量理论,经过一系列的变换可以得到功率系数另外一种表达式:

风力机叶片是由复合材料加工制造而成,叶片密度变化不一,其曲面形状非常复杂,采用传统的复合材料层合板理论很难建立叶片的质量理论计算模型,因此,在其他条件一致的情况下(叶片铺层厚度及密度),将叶片的质量计算转化为叶片曲面面积计算模型,要使质量最小,意味着对应的叶片表面面积最小。图5为叶片面积计算示意图,叶片曲面面积最小作为目标优化之一:


图5 叶片曲面面积计算示意图Fig.5 The blade surface area calculation schematic
f(x,y)为叶片沿展向r处截面轮廓线长度方程,采用微积分的形式来表达此函数:

xi、yi为三维空间叶片截面数据点坐标,如果数据点足够多,将会无限接近截面曲线长度。根据叶片空间坐标几何变换原理,可以将沿展向r处的叶片截面坐标(xi,yi)表示成:

其中x,y为叶片沿展向r处翼型的空间坐标,x0,y0为单位弦长翼型在二维平面的坐标,c为叶片沿展向r处的弦长,β为叶片沿展向r处的几何扭角。
联立方程(13)~(15),采用微积分的方法即可求出整个叶片曲面的面积。
由上面两个目标函数可知,该叶片优化过程实质上是一非线性双目标函数优化数学模型。为求解方便,本文通过设定权值系数将多目标优化问题转化为单目标优化函数:

式中,μ1为权值系数,μ1∈[0,1];为使两个目标函数为同一个数量级,在这里给定一个比例因子ratio,一般最大功率系数在0.5附近,那么为了使两个优化目标函数重要程度相当,F2(X)/ratio也应该是这一数量级。
2.2.2 设计变量及约束条件
叶片的曲面形状决定了风力机捕获风能的效率,而叶片的长度、弦长、扭角及相对厚度直接构成了叶片的形状。风轮的半径选取常值为31m,由表3可知,标准翼型沿叶片展向位置是确定的,叶片的厚度分布即可通过插值的方法确定,因此选取叶片的弦长、扭角作为优化设计变量。为了避免因翼型族的不同而使优化结果对比没有意义,叶片初始几何外形参数选择传统的欧盟2MW Tjære型叶片(采用NACA44XX系列翼型)相关参数,该叶片的具体参数(弦长及扭角分布)见参考文献[4];同时针对同一功率大小不同翼型族的风轮性能进行研究(假设叶片长度、弦长分布和扭角分布不变)。
针对叶片的弦长,为了保证叶片拥有良好的气动特性及表面连续光滑性,本文选取关键的8个点(标准翼型沿叶片展向分布的点),采用样条曲线来对弦长及扭角的展向分布进行控制,这样设计变量总共就有16个,其取值范围控制在(表4给出了优化设计变量的约束范围)
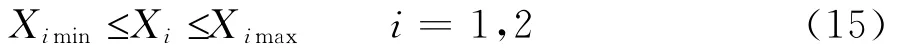

表4 优化设计变量的约束范围Table 4 The constrained range for optimized design variables
另外在优化设计中,还需对叶片的载荷进行控制约束。叶片的载荷由叶素动量理论计算得出。基于风力机空气动力学理论知,叶片的法向力系数Cn和切向力系数Ct表示为

式中L为翼型的升力系数,D为翼型的阻力系数。
在风轮工作时,叶根处的弯矩很大,弯矩的增加会直接影响着叶片强度及风力机的疲劳寿命,而叶根处的弯矩主要为挥舞弯矩和摆振弯矩,挥舞弯矩是由推力而产生,摆振弯矩则是由切向力分布产生的在风轮平面内的弯曲力矩,由于摆振弯矩的大小很大程度上受到叶片重力的影响,气动载荷影响较小,弯矩图表现出明显的正弦变化,而挥舞弯矩主要受到气动载荷的影响[16],因此,不考虑摆振弯矩约束,对叶根挥舞弯矩进行了约束。

此外,风轮的扭矩由叶片所受的切向力而形成的,扭矩的大小直接决定了风力机的输出功率,理论上讲,输出功率随转矩的增加而增加。但是,转矩过大会使风力机传动系统的载荷增加,不利于机械传动系统的使用寿命。因此,对风轮的扭矩也进行了约束控制

3 优化设计结果
基于修正的空气动力学模型,给定一定的初始条件,设定容许误差,通过不断的迭代,由式(5)和(6)可以计算出叶片的轴向诱导因子a和周向诱导因子a′,进而就可以得到叶片上的作用力和功率等。采用改进的多目标粒子群算法,编制程序进行优化求解。由于粒子群算法中有些基本参数不定,优化时需要根据具体问题不断调试参数进行迭代,经过多次迭代,作者发现选取如下参数时该改进粒子群算法优化效果及收敛速度良好:惯性权重w取0.9,学习因子C1、C2均取0.5,变量维数为16,种群大小为50,最大迭代次数为200,权值系数μ1为0.25,比例因子ratio为500。叶片具体优化设计计算流程图如图6所示,明确目标函数、设计变量及约束条件;以叶片弦长和扭角为变量初始化粒子群,采用计算机图形学中的样条曲线将粒子群集插值得到弦长、扭角分布曲线;然后基于动量叶素理论及叶片曲面面积积分,计算适应度值;然后根据适应度值更新相应的粒子群参数,判断是否满足迭代终止条件,否则继续迭代,是则输出最优值。其中翼型的气动参数采用RFOIL计算,然后采用外插值方法生成翼型±180°攻角范围的气动参数。
图7、图8给出了优化后叶片弦长及扭角分布图,将该优化结果与优化前初始叶片进行了比较。由图7可以看出,新设计的叶片弦长沿展向分布呈现出非线性特性,从整体上看,每个叶素的弦长都要小于初始叶片,在叶片的中部尤为明显,这是由于将叶片的曲面面积最小作为目标函数之一,因此算法将会朝着有利于减少叶片面积降低叶片质量的趋势发展;由图8可以看出,新设计的叶片扭角分布也呈现出非线性特性,在叶片根部附近扭角要明显大于初始叶片,而叶尖处相差不太,叶片的扭角增大会减小叶片根部的载荷,进而增加叶片的使用寿命,有利于降低叶片的成本。

图6 叶片优化设计算法流程图Fig.6 The blade optimized design algorithm flowchart
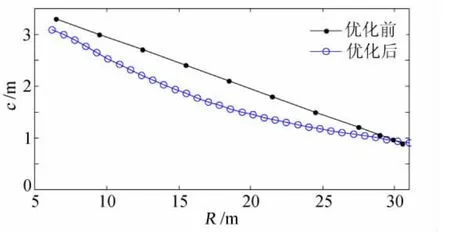
图7 弦长分布Fig.7 The distribution of the chord length

图8 扭角分布Fig.8 The distribution of the twist
图9为Tjære叶片、优化前叶片和新设计叶片的功率系数随叶尖速比变化的曲线图。由图9可知,初始叶片在设计叶尖速比下(2~7.5)的功率系数要明显大于欧盟Tjære实验叶片,主要原因是由于翼型族的不同而使其气动性能不同造成的;而新设计的叶片在设计叶尖速比下(6~12)功率系数要明显大于初始叶片,这主要是由于叶片外形参数不同而引起的。图10给出了在相同条件下新设计的风轮年均发电量特性随风速的变化曲线,相比优化前及Tjære风轮,在额定风速内(V≤12.5m/s),优化后的风轮年发电量分布有了较大的提高,当风速达到额定风速后,通过传动控制及变桨距调节系统使功率控制在2MW,这样年均发电量及功率将保持不变。

图9 功率系数特性Fig.9 The characteristics of the power coefficient

图10 年均发电量分布Fig.10 The distribution of the annual generating capacity
表5为Tjære风轮、初始叶片以及新设计的2MW叶片各项性能指标对比。结合上图及表5可知,初始叶片在最大功率系数、年发电量方面均优于Tjære型风轮,但是叶根载荷、风轮扭矩均大于Tjære型风轮;而相比初始2MW叶片,新设计的风轮叶片,最大功率系数为0.50830,提高了4.019%,年发电量为4.406×106kWh,提高了1.967%,风轮面积为278.906m2(0.2R~1.0R 处),减少了19.005%,这意味着在其他叶片内部结构不变的情况下风轮的质量有了大幅度的减少,提高了叶片的疲劳寿命,降低了叶片的材料成本。由于采用全新的高性能的风力机翼型,较大的气动力会增加叶根载荷,通过该设计及优化方法,风轮叶根的弯矩和扭矩均有所减少,且叶根弯矩减少尤为明显,表明该设计方法能够有效地控制叶根载荷。

表5 新设计叶片与传统叶片各项性能对比Table 5 The comparison of the performances for the new design blade and the traditional blade
4 结 论
(1)在整个叶片设计上采用作者全新设计的风力机翼型系列CQU-A,验证了该翼型系列具有较高的气动性能;基于修正的风力机空气动力学理论,提出了以最大功率系数及最小叶片面积为多目标优化模型,以弦长、扭角为设计变量,建立了新型风力机叶片设计及优化数学模型。
(2)应用该设计模型,采用改进的多目标粒子群算法对风力机叶片进行优化设计,并将优化结果与初始叶片、Tjære实验叶片进行对比分析,优化结果表明,相比初始叶片及Tjære叶片,新设计2MW风力机叶片的最大功率系数及年发电量均有所提高,而且叶片表面面积具有显著的下降,这意味着在其他叶片内部结构不变的情况下极大的减少了叶片的质量,提高了叶片的疲劳寿命,降低了叶片的材料成本;同时叶根载荷也得到了有效的控制。该新型叶片的研究为设计出高性能轻质量低成本的风力机提供了理论依据。
[1]BADREDDINNE K,ALI H,DAVID A.Optimum project for horizontal axis wind turbines‘OPHWT′[J].Renewable Energy,2005,30:2019-2043.
[2]刘雄,陈严,叶枝全.遗传算法在风力机风轮叶片优化设计中的应用[J].太阳能学报,2006,27(2):180-185
[3]韩中合,吴铁军.基于遗传算法的风力机叶片优化设计[J].动力工程,2008,28(6):955-958.
[4]WANG Xudong,SHEN W Z,ZHU W J,et al.Shape optimization of wind turbine blades[J].Wind Energy,2009,12:781-803.
[5]JACKSON K J,ZUTECK M D,VAN D C,et al.Innovative design approaches for large wind turbine blades[J].Wind Energy,2005,8:141-171.
[6]杨从新,宋显成.一种大型风力机叶片的气动优化设计方法[J].空气动力学学报,2011,29(2):222-229.
[7]王珑,王同光,罗源.改进的NSGA-Ⅱ算法研究风力机叶片多目标优化[J].应用数学与力学,2011,32(6):693-700.
[8]RAJAKUMAR S,RAVINDRAN D.Iterative approach foroptimizing coefficient of power,coefficient of lift and drag of wind turbine rotor[J].Renewable Energy,2012,38:83-93.
[9]KEVIN Maki,RICARDO Sbragio,NICKOLAS Vlahopoulos.System design of a wind turbine using a multileveloptimization approach[J].Renewable Energy,2012,43:101-110.
[10]RONIT K Singh,RAFIUDDIN Ahmed M.Blade design and performance testing of a small wind turbine rotor for low wind speed applications[J].Renewable Energy,2013,50:812-819.
[11] 贺德馨.风工程与工业空气动力学[M .北京:国防工业出版社,2006:87-90.
[12]SHEN W Z,MIKKELSEN R,SØRENSEN J N,et al.Tip loss correction for wind turbines computations[J].Wind Energy,2005,8:457-475.
[13]陈进,张石强,王旭东,等.基于粗糙度敏感性研究的风力机专用翼型设计[J].空气动力学学报,2011,29(2):142-149.
[14] SHEN WZ CHEN J CHENG J T et al.Airfoils and methods for designing airfoils[P].Application No.PCT/EP2010/056810,International patent application.
[15]FUGLSONG P,BAK C.Development of the Risøwind turbine airfoils[J].Wind Energy,2004,7:145-162.
[16]肖劲松.风力机空气动力学[M].北京:中国电力出版社,2010,87-89.

