基于致动线方法的风力机气动数值模拟

朱 翀，王同光，钟 伟

（南京航空航天大学 江苏省风力机设计高技术研究重点实验室，江苏 南京 210016）

0 引 言

为了获得风力机叶片的气动性能，目前使用的最主要的工具是结合二维翼型性能数据的叶素动量（BEM）理论。由于其简便性，工业应用中使用BEM理论设计新的风力机叶片。然而，为了获得风力机周围流场的精确信息，为了获得风力机或风力机组更精确的载荷信息和发电功率等，需要更精致的技术，比如计算流体力学（CFD）方法［1－3］。目前 CFD 方法已经成为研究风力机空气动力学的常用工具。然而在使用CFD方法对风力机尾流流场进行研究时，为了同时满足风力机叶片附近区域和尾流区域的数值精度需要大量网格和很高的计算成本，这限制了CFD方法在风力机尾流流场研究中的应用。结合BEM理论的简便性与CFD方法对流场的精确模拟性，Shen等学者提出了致动线（AL）方法［4］。Troldborg在其博士论文中使用致动线方法对Tjæreborg叶片与NM80叶片进行了数值模拟［5］；Shen使用致动线方法对MEXICO实验叶片进行了数值模拟［6］，均取得了较理想的结果。而在国内，致动线方法尚未有较系统的研究。

致动线方法是融合了引入沿叶片展向分布的体积力代表风力机叶片的致动线技术与三维Navier－Stokes方程的一种方法。风力机叶片绕轴旋转，产生气动力，从流体微团的角度来看，流体微团感受到的是动量的变化，故通过在Navier－Stokes方程中引入动量源项（即体积力）来表示叶片的这种作用。因此致动线方法的优势在于使用体积力来代替风力机叶片，其所需要的网格单元数远远小于为了捕捉叶片几何细节所耗费的网格单元数，而且在计算过程中也避免了花费大量资源去计算叶片附面层，可以把更多的网格与计算资源投入到风力机的尾流区域，最终的计算结果中包含的流场信息（比如速度、压力、涡量等各种参数）也不比CFD方法获得的少，所以致动线方法是研究风力机尾流流场的很好的工具，国外的学者在使用致动线方法研究风力机尾流流场方面已经取得极大的进展［4－6］。致动线方法与CFD方法都是通过Navier－Stokes方程组来求解流场信息的，所以在数值精度方面应该是完全一样的。在计算结果的准确性方面，虽然致动线方法使用体积力代替风力机叶片，无法获得叶片附面层流场的信息，但其使用了风洞实验测得的翼型气动力数据，一定程度上弥补了以上简化造成的计算结果准确性的降低。而BEM理论虽然能够快速得到叶片的载荷、功率等信息，但是完全无法获得相关的流场信息。因此致动线方法在风力机研究方面有其独特的优势。但是由于代替叶片的体积力是由二维翼型性能数据计算而得，故致动线方法非常依赖于所提供的二维翼型性能数据的准确性。

本文使用致动线方法对南京航空航天大学自主研发的NH1500叶片进行数值模拟，并将致动线方法的数值模拟结果与BEM理论、CFD方法的数值模拟结果以及风洞实验［7］结果进行了系统的比较，来突显致动线方法区别于BEM理论与CFD方法独特的优势。

1 致动线方法

1.1 控制方程

本文数值模拟使用基于有限体积法的解算器。将风力机周围流场看作不可压有粘流动，故求解的控制方程组为旋转参考系下的不可压雷诺平均Navier－Stokes方程组，其表达式为：

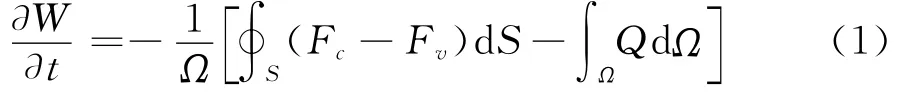
式中：Ω为以S为边界的控制体；W 表示守恒变量；Fc表示对流通量；Fv表示粘性通量；Q表示体积力源项。W，Fc，Fv，Q 的表达式如下：

式中：n为单位法向量；ρ为空气密度；u，v和w 为速度的三个分量；p为压强为剪切应力；fe为参考系旋转导致的体积力加速度；fε为代表叶片作用的体积力，将在后面进行详细的推导；

逆变速度V的表达式为：

方程组中各个变量都是定义在旋转参考系下的，该参考系的转轴与风力机风轮转轴重合，转速与风轮转速相同，是一个非惯性参考系。为了修正因参考系旋转而附加给气流的离心力和科式力，在方程组中定义体积力加速度为：

式中：ω为参考系的旋转角速度；r为位置矢量。

本文采用对边界层湍流和自由剪切湍流都有较好模拟效果的SST k－ω模型［8］来计算湍流粘性。

1.2 叶片气动模型

代表风力机叶片的体积力是基于叶素假设，根据当地的流场信息与已知的二维翼型性能计算所得。图1为叶片的一个翼型截面图，其中x方向为来流方向。

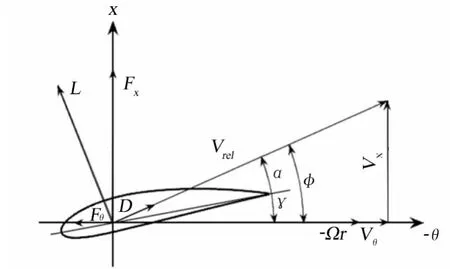
图1 叶片的翼型截面Fig.1 Cross－sectional airfoil element of blade

叶片翼型截面的当地速度为：

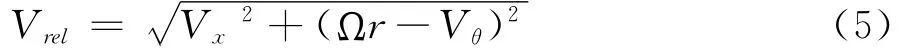
其中，Ω为角速度，r为叶片翼型截面径向位置，Vx和Vθ分别为叶片翼型截面的轴向速度和切向速度。

轴向速度

切向速度

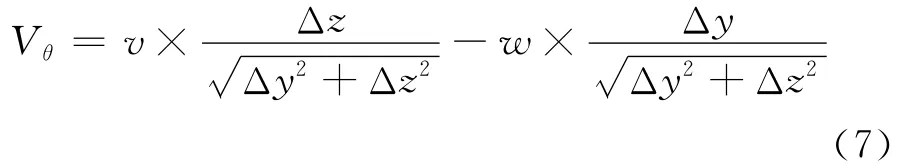
本文计算使用坐标系为笛卡尔坐标系，叶片位于平面x＝0内。u、v、w分别为流场中叶片翼型截面x、y、z方向的速度，Δy和Δz为叶片翼型截面与叶根在y和z方向上的距离。

叶片翼型截面的当地速度与风力机叶片平面之间的夹角为：

叶片翼型截面的当地迎角为：

其中γ为当地桨距角。

在确定了叶片翼型截面当地速度与当地迎角之后，即可以得到单位展长的升力与阻力：

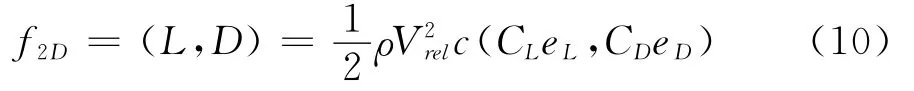
其中CL＝CL（α，Re）和CD＝CD（α，Re）分别为升力系数和阻力系数，Re为基于当地弦长c的雷诺数，eL和eD为升力和阻力方向的单位向量。

1.3 高斯分布

为了使代表叶片的体积力在流场中光顺的分布，将体积力在流场中以致动线为中心线呈三维高斯分布［4］。

经过高斯分布的单位体积力为：

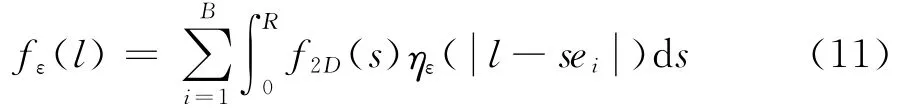
分布因子：

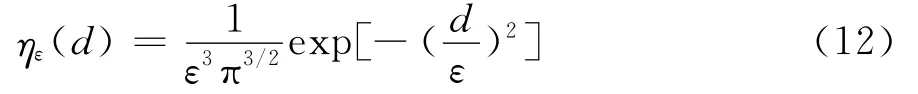
其中d＝｜l－sei｜为网格单元中心点与致动线上第i个点之间的距离，ε为控制气动力分布的分布因子。

最后，将分布后的单位体积力fε（l）作为体积力源项加载到CFD计算的动量方程中，即为方程（1）中的体积力源项Q中的fε。而其他的物理量（如速度、压力等）则通过求解方程（1）而得。

2 计算模型与计算条件

计算模型选用南京航空航天大学自主研发的NH1500风力机，该风力机为三叶片式，叶片长度为40.5m。选择4个具有代表性的运行状态进行计算，具体计算状态见表1，其中Vin为入流风速，Ω为风轮转速，λ为叶尖速比。

表1 计算状态Table 1 Computational states

致动线方法的计算域结构如图2所示，速度入口距离致动线为5倍风轮半径，压力出口距离致动线为20倍风轮半径，远场边界距离中心线为9倍风轮半径。针对NH1500风力机三叶片的轴对称特点，应用了120°旋转周期边界条件，使得计算域只有实际区域的三分之一，从而使网格单元数和计算量减少。周期边界上一侧的网格节点和另一侧的网格节点一一对应，紧邻周期边界一侧的计算域外的“镜像单元”信息由紧邻另一侧的计算域内的单元提供。为了充分利用网格，将计算域分为内场和外场，内场为致动线附近的区域，对该区域的网格进行加密处理，而外场区域内的网格则较为稀疏。实际计算域网格拓扑结构如图3所示。整个计算域采用六面体网格，网格单元数为1.5×106。

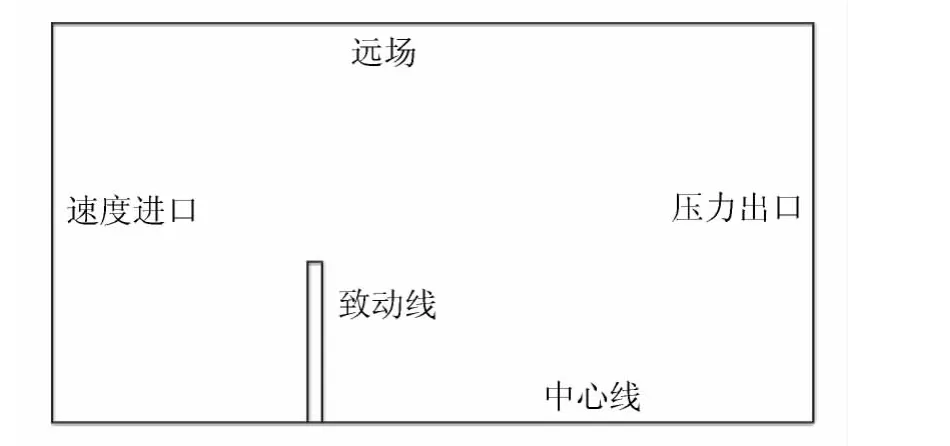
图2 计算域结构图Fig.2 Structure diagram of computational domain

图3 计算域网格拓扑结构Fig.3 Topology of computational domain

为了验证致动线方法的可行性，除了使用致动线方法，还使用了BEM理论与CFD方法对NH1500叶片进行了数值模拟作为参照。其中BEM理论［9－10］主要是以成熟商业软件BLADED作为参照而编写的，考虑了经典的普朗特叶尖损失修正［11］，计算结果与BLADED软件计算结果相一致。CFD方法则是对NH1500叶片的附面层进行了精确的数值模拟，计算区域及网格拓扑结构与致动线方法网格基本一致，网格单元数为4×106。

用于研究NH1500叶片气动性能的风洞实验是在中国气动研究与发展中心12m×16m的低速风洞中完成的。

3 分布因子ε的选取

分布因子ε是致动线方法中非常重要的一个参数，它关系着体积力的分布范围，是能否合理表现出叶片在流场中作用的关键。在此对不同分布因子ε的数值模拟结果进行比较分析。一般情况下，分布因子ε的取值都是网格中致动线部分的网格单元尺寸的倍数，即ε＝n×Δs，其中n为倍数，Δs为致动线网格单元的尺寸。如果分布因子ε选取过小，则体积力在流场中作用范围过于集中，与实际叶片对流场的影响不相符，导致计算结果与真实情况相差较大，同时还可能会影响计算的收敛性。如果分布因子ε选取过大，则会使体积力在流场中作用范围过大，影响叶尖流场的分布，这当然也是与实际叶片对流场的影响不相符的。

以入流风速V0＝9m／s的情况为例进行分析，以n作为变量，分别取1，1.5，2，2.5，3，3.5，4。图4为不同分布因子ε下沿叶片展向分布的切向力因子Ct，图中还增加了CFD方法数值模拟的结果作为参照。由图4可以看出，当n取1的时候，计算所得的切向力因子Ct明显过小。这说明n取1时，因体积力的分布范围过于集中而不能真实合理的反映叶片在流场中的作用，从而该计算结果错误。而当n取1～4时，计算所得的切向力因子Ct在叶片大部分区域基本相同，只在叶尖处有区别；n取4时，叶尖处的切向力因子Ct有明显的突变。这说明n取4时，体积力的分布范围过大，影响了叶尖的流场分布。综合比较得出当n取2时，体积力的分布较为合理，能够真实反应叶片对周围流场区域的影响。

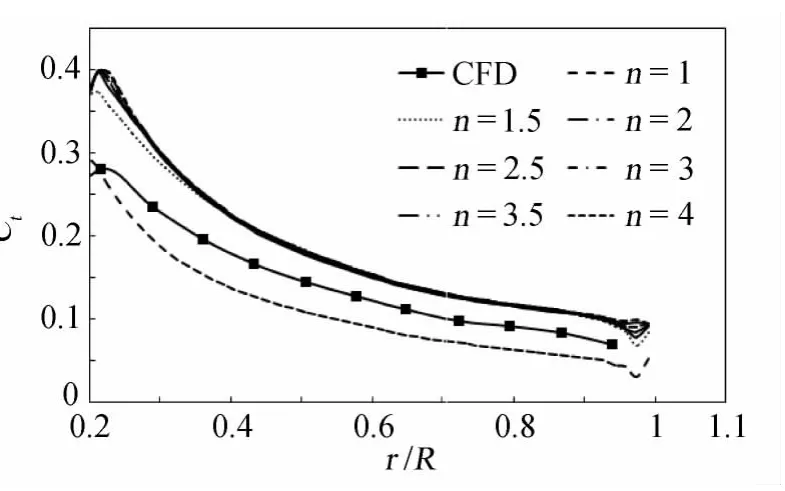
图4 沿叶片展向分布的切向力因子CtFig.4 Tangential force coefficient Ct distributed along the blade

因此分布因子的选择将会影响叶片气动力的计算以及代表叶片作用的体积力在流场中的作用范围，选择合适的分布因子才能够获得较准确的叶片流场。

4 数值模拟结果与分析

4.1 载荷分布

图5为入流风速8m／s下致动线方法、BEM理论、CFD方法计算出的沿叶片展向的法向力系数Cn和切向力系数Ct分布，其中横坐标为叶片当地展向位置与叶片长度的比值，纵坐标分别为法向力系数Cn和切向力系数Ct。由于三种方法中对叶根处的处理方法并不相同，导致叶根处结果相差较大，不具有参考价值；且叶根处的发电量在整个叶片发电量中所占比例极小，故在此不考虑叶根处的情况。

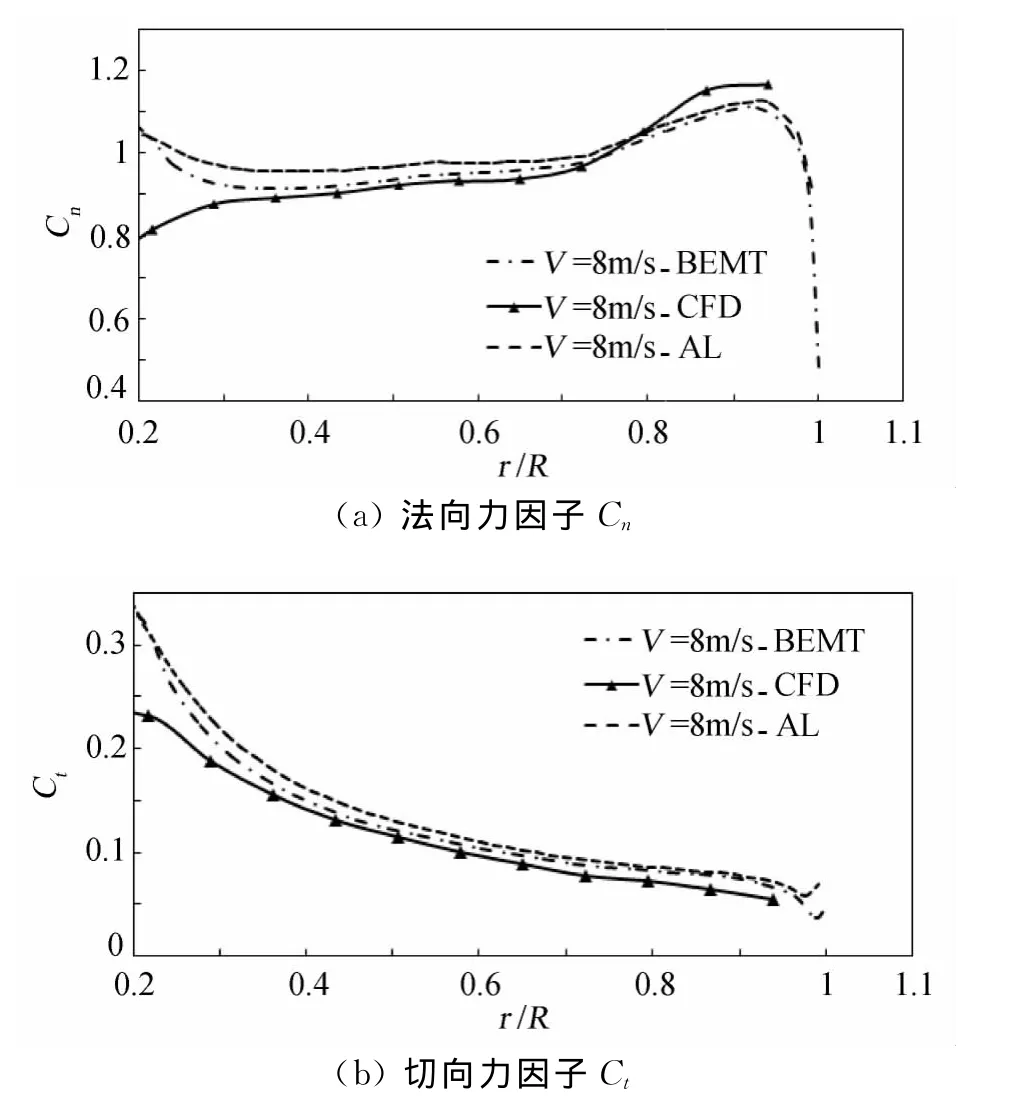
图5 沿叶片展向分布的法向力因子Cn与切向力因子CtFig.5 Normal force coefficient Cn and tangential force coefficient Ct distributed along the blade

总的来说，图5中三种方法计算所得的沿叶片展向的法向力系数Cn和切向力系数Ct分布趋势大致相同。但是致动线方法与BEM理论的计算结果更为接近，这是因为致动线方法与BEM理论都是通过二维翼型性能插值计算得到各个截面的气动力，进而计算出其它相关信息；而CFD方法则是完全通过对流场的数值模拟得到所有的信息。致动线方法把得到的各个截面的气动力通过体积力的方式作用到流场中，再通过求解Navier－Stokes方程得到叶片性能及周围流场的信息；BEM理论则是将叶片离散成一个个截面，通过一维动量守恒定律进行分析，相邻截面互不干扰。致动线方法中叶片不同截面之间是有相互影响的，而BEM理论中不同截面之间是互不干扰的，这也是致动线方法与BEM理论的一个区别。

除了所使用的计算方法对结果造成的影响，致动线方法与BEM理论计算所需的二维翼型性能数据对计算结果有更大的影响。入流风速8m／s下，致动线方法计算所得的沿叶片展向的法向力系数Cn和切向力系数Ct要大于BEM理论的，而BEM理论的大于CFD方法的。这是因为致动线方法与BEM理论计算所用的二维翼型风洞实验性能数据是雷诺数3×106下的，远远大于入流风速8m／s时叶片各截面真实的雷诺数，过大的雷诺数导致计算出的气动力偏高，从而使致动线方法与BEM理论的计算结果较CFD方法要偏大。而且叶片展向各个翼剖面的雷诺数也并不相同，使用同一雷诺数的翼型气动力数据来计算，也会使结果产生一定的误差。

而在叶尖处CFD方法计算所得的法向力系数Cn和切向力系数Ct却大于致动线方法与BEM理论计算所得的，这是因为叶片叶尖由于叶尖绕流效应的存在而使周围流场三维效应显著。虽然BEM理论已经考虑了经典的普朗特叶尖损失修正，但是毕竟普朗特叶尖损失修正是经验公式，不可能完全体现出叶尖效应；而CFD方法是对叶尖直接进行模拟，故应该可以较好的体现出叶尖效应，但是由于叶尖处并不是常规的翼型形状，在叶尖采集处理所得的法向力系数Cn和切向力系数Ct会有一些误差，故CFD方法中的Cn、Ct只采集到叶片的展向94%位置处。而致动线方法在没有使用任何经验公式修正的情况下，计算所得叶尖处的Cn、Ct与BEM理论使用了普朗特叶尖损失修正的计算所得的Cn、Ct已经比较接近了，与CFD方法计算所得有一些小差距。这是因为虽然说致动线方法是通过直接求解Navier－Stokes方程来获得叶尖附近的流场信息，能够通过代表叶片作用的体积力来模拟叶尖绕流效应，不同于无粘假设的BEM理论，不需要使用传统的普朗特叶尖损失修正公式来对叶尖进行修正。但是由于叶尖绕流造成的三维效应，靠近叶尖处的翼型截面性能不再是二维的，而致动线方法所使用的翼型性能数据却是二维的。

4.2 功率系数

风力机功率系数Cp是风力机叶片的主要气动性能参数，体现了风力机叶片的发电效率，是衡量风力机叶片气动性能优劣的重要指标。图6为NH1500叶片在不同叶尖速比下风洞实验、CFD方法、致动线方法所得的功率系数。从图6中可以看出无论是风洞实验还是CFD方法或致动线方法，都是在叶尖速比为9.5左右取得最大功率系数Cp。风洞实验的最大功率系数Cp为0.492，CFD方法的为0.505，致动线方法的为0.521。不仅仅是风洞实验获得的最大功率系数Cp要略小于CFD方法与致动线方法计算所得的最大功率系数Cp，而且所有实验获得的功率系数Cp都略小于CFD方法与致动线方法相对应叶尖速比下的功率系数Cp。由于风洞实验中所使用的为1／16的模型，其雷诺数必然是小于CFD方法与致动线方法中的雷诺数，造成了风洞实验中叶片的升力偏低而阻力偏高，这也就解释了CFD方法与致动线方法所得的功率系数Cp要略大于风洞实验的功率系数Cp。而致动线方法所得的功率系数Cp则要比CFD方法的略高一些，是因为致动线方法中所使用的二维翼型性能数据为雷诺数3×106下的，与CFD方法中的雷诺数相比偏高；且在高叶尖速比，也即低风速下，两种方法中雷诺数的差距更大，所得的功率系数Cp相对而言相差也更大一些。

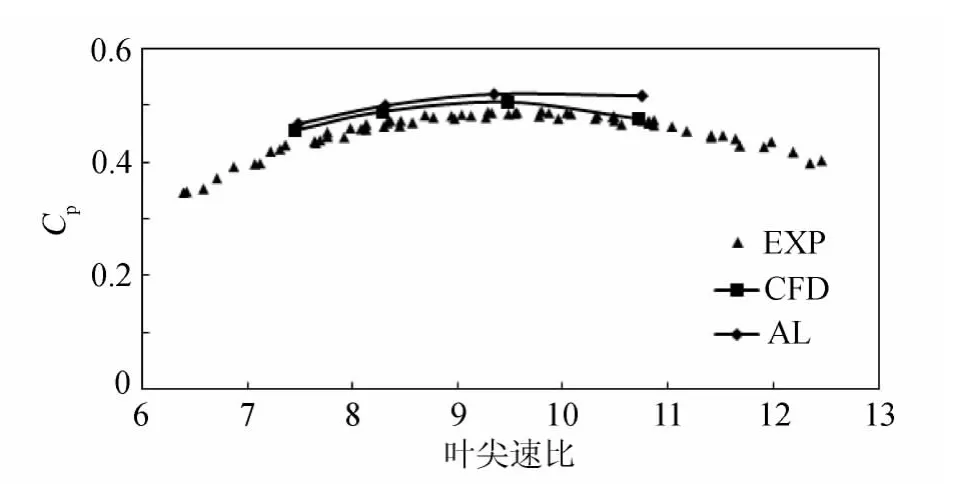
图6 功率系数CpFig.6 The power coefficient Cp

5 尾流区域的简要分析

叶片压力面的压力高，吸力面的压力低，压力差推动气流绕过叶尖，形成叶尖涡。风力机的叶尖涡在来流风速的叠加下，不容易从迹线或速度矢量上直接显示出漩涡的位置，因而引入涡量来显示涡。图7是使用致动线方法计算的入流风速9m／s下拖出的叶尖涡的涡量等值面，左右两个平面上显示的是轴向速度等值线。从图7中可以清晰的看出从叶尖拖出的叶尖涡在尾流区域呈螺旋结构向下游发展，其诱导速度以一定的周期性规律作用于尾流流场。

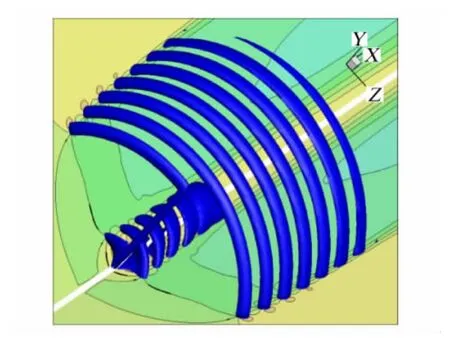
图7 尾流的涡量等值面和轴向速度等值线图Fig.7 Isosurface of the vorticity and contours of the axial velocity in the wind turbine wake flow filed

为了更好的观测尾流区域流场的变化，取叶片所在的轴向平面的轴向速度等值线图，如图8所示。图8中，通过叶尖涡对尾流流场的诱导作用可以清楚的看出叶尖涡在尾流区域是呈膨胀趋势向下游发展。这一系列的结论都是与CFD方法对尾流区域叶尖涡发展趋势的研究结论［12－15］相一致的。这也验证了使用致动线方法研究尾流流场的可行性。

图8 轴向速度等值线图Fig.8 Contours of the axial velocity

为了准确的分析尾流区域流场的计算精度，选取轴向诱导因子这一典型流场参数进行研究。图9为叶片所在的轴向平面的轴向诱导因子等值线图，横轴为风力机风轮下游位置x与风轮半径R的比值，纵轴为风轮径向位置y与风轮半径R的比值。图中横坐标为0处黑线代表叶片的位置。从图9中可以看出叶片和叶片周围的轴向诱导因子接近1／3，这与经典动量理论中气动性能最优的风力机是一致的。尾流区域的外部和中间的诱导因子都要小于尾流区域的主体部分。很明显的是，轴向诱导因子从叶片位置向下游方向不断增加，即是轴向速度不断减小。在叶片下游远方，轴向诱导因子最终达到了0.5，是叶片和叶片周围诱导因子的两倍，这也验证了经典动量叶素理论的假设。

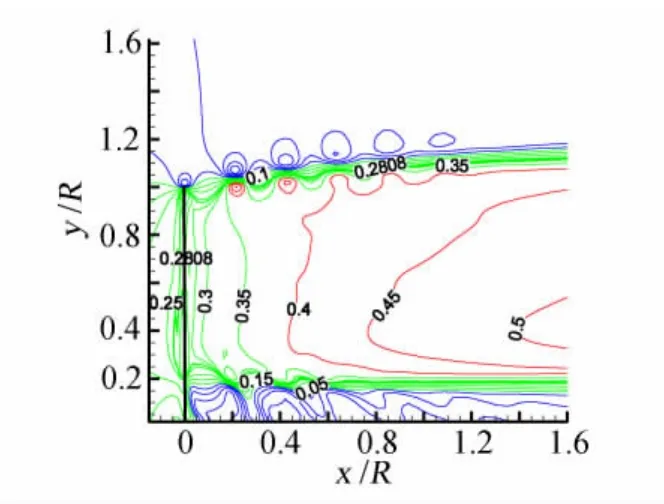
图9 轴向诱导因子等值线图Fig.9 Contours of the axial induced factor

6 结 论

本文以南京航空航天大学自主研发的NH1500叶片为计算模型，使用致动线方法、BEM理论与CFD方法分别进行了数值模拟。并且与风洞实验进行了比较。通过系统的比较，在对流场细节的捕捉方面，致动线方法的计算精度已经达到了CFD方法的计算精度，与风洞实验吻合。为了捕捉风力机叶片的附面层，CFD方法耗费了大量网格与计算资源，而致动线方法则不需要去求解风力机叶片附面层，可以把更多的网格与计算资源投入到风力机尾流流场。因此致动线方法相比于CFD方法，节约了大量的网格与计算资源，却能够达到CFD方法对风力机尾流流场模拟同样的精度，最终的计算结果中包含的流场信息也不比CFD方法获得的少。而BEM理论则完全不能够获得风力机叶片周围的流场信息。因此致动线方法是研究风力机尾流流场的有力工具，特别是对于风场中多台风力机之间的相互干扰的研究，致动线方法的优势相比于CFD方法更加明显。但是致动线方法中使用的二维翼型性能数据的准确性在一定程度上也制约着致动线方法的发展。研究三维效应对二维翼型性能的影响，使翼型性能数据满足致动线方法计算的需求，将有利于提高致动线方法的准确性。

［1］SANDERSE B，Van Der PIJL S P，KOREN B.Review of computational fluid dynamics for wind turbine wake aerodynamics［EB／OL］. ［2011－02－04］.http：／／onlinelibrary.wiley.com／doi／10.1002／We.458／abstract

［2］VERMEER L J，SØRENSEN J N，CRESPO A.Wind turbine wake aerodynamics［J］.Progress in Aerospace Sciences，2003，39（6／7）：467－510.

［3］王琦峰，陈伯君，安亦然.大型风力机三维空气动力学数值模拟［J］.空气动力学学报，2011，29（6）：810－814.

［4］SØRENSEN J N，SHEN W Z.Numerical modeling of wind turbine wakes［J］.Journal of Fluids Engineering，2002，124：393－399.

［5］TROLDBORG N.Actuator line modeling of wind turbine wakes［D］.Denmark：Technical University of Denmark，2008.

［6］SHEN W Z，ZHU W J，SØRENSEN J N.Actuator line／Navier－Stokes computations for the MEXICO rotor：comparison with detailed measurements［EB／OL］.［2011－10－03］.http：／／onlinelibrary.wiley.com／doi／10.1002／we.510／abstract

［7］肖京平，陈立，许波峰，武杰.1.5MW风力机气动性能研究［J.空气动力学学报，2011294529－534.

［8］MENTER F R.Two－equation eddy－viscosity turbulence models for engineering applications［J］.AIAA Journal，1994，32（8）：1598－1605.

［9］GLAUERT H.Aerodynamic theory，vol.4［M］.Berlin，Germany：Julius Springer：1935：169－360.

［10］MARTIN O L，Hansen.Aerodynamics of wind turbines（2nd Edition）［M］.UK：Earthscan，2008，45－62.

［11］PRANDTL L，BETZ A.Vier Abhandlungen zur hydrodynamik und aerodynamik［C］.Göttingen，city，1927：88－92.

［12］钟伟，王同光.风力机叶尖涡的数值模拟［J］.南京航空航天大学学报，2011435640－644.

［13］PORTE－AGEL F，WU Y T，LU H，et al.Large－eddy simulation of atmospheric boundary layer flow through wind turbines and wind farms［J］.Journal of Wind Engineering and Industrial Aerodynamics，2011，99（4）：154－168.

［14］JOHANSEN J，SØRENSEN N N，MICHELSEN J A，et al.Detached－eddy simulation of flow around the NREL phase VI blade［J］.Wind Energy，2002，5：185－197.

［15］杨瑞.水平轴风力机尾流结构及空气动力学性能的研究［D］.中国：兰州理工大学，2009.