用于空间手势输入的无陀螺微惯性测量单元设计*

王祥雒,杨春蕾,郑瑞娟

(1.洛阳师范学院信息技术学院,河南 洛阳 471022;2.河南科技大学信息工程学院,河南 洛阳 471000)

有别于物理键盘、手写板、触控屏幕等传统二维输入方法,空间手势输入[1]技术通过提取手持式测量单元的角速度、线加速度等原始特征,经计算得到手势轨迹,并利用模式识别等手段实现数字、字符等信息的输入[2-3]。空间手势输入具有高灵活性、符合人类自然习惯等特点,是当前研究的一个热点。

手势特征提取的关键是利用惯性传感器件的输出得到复合加速度和角速度并解算线加速度,从而提取手势的线速度、线性运动轨迹等特征,其基本原理是惯性导航技术。目前,常见的惯性测量单元设计一般采用MEMS加速度计与MEMS陀螺仪的组合方案[4],或者仅进行二维特征提取的单MEMS加速度计简化方案[5]。但MEMS陀螺漂移较大,无法适应大角速度测量,抗大线加速度冲击能力差,使用MEMS加速度计和MEMS陀螺组合方案的可靠性低,且成本较高;而仅使用单个加速度计的简化方案,对手势区域有严格限制,灵活性较差。

自DiNapoli、Schuler首次提出无陀螺角速度测量方法以来[6-7],国内外学者对无陀螺惯性导航的原理、方法进行了广泛深入的研究,Merhav S J、Alfred R Schuler、LEE Souchen、LIU Cheng-Yu等人的工作最具代表性[8-9]。近年来,国内也出现了将无陀螺惯性导航原理应用于飞行器导航,手写数字输入、人体运动模式识别等领域的大量研究成果,其中,六加速度计和九加速度计配置方案[10-11]的传感器空间布局复杂,不适合小型化应用;使用单个三轴加速度计配合软件插值估计角速度的方法精度有限[12-13],由于学习样本仅有两个,在复杂姿态变化场合该方法可能无效。

本文讨论三维空间手势的加速度特征提取问题,重点阐述仅使用MEMS加速度计构建微惯性测量单元的传感器配置方案、相应的角速度、线加速度解算及积累误差补偿方法。该方法具有以下特征:(1)使用两个三轴MEMS加速度计实现角速度、线加速度解算,避免使用陀螺仪组件,从而提高方案的可靠性;(2)在保证手势特征解算快速准确性的同时,加速度计在长轴方向上的对称布局有利于相应手持设备(如笔形手势输入装置)的硬件设计,有效降低成本、满足小型化的要求。

1　手势特征提取的基本原理

手势输入过程中,测量单元随手势做线性和旋转的复合运动,即测量单元在某一书写平面移动的同时,其姿态也发生变化。手势特征提取是指利用惯性传感器件的输出得到复合加速度和角速度,并解算出线加速度,为下一步提取手势的线速度、线性运动轨迹等特征提供依据。实现手势特征提取一般需在测量单元上安排陀螺仪和加速度计,而对于仅使用加速度计的无陀螺方案,则需要通过多个安排在非质心处的加速度计组合来解算角速度和质心处的实际线加速度。

设OeXeYeZe为当地地理坐标系,OeXeYe为地平面,将手势测量单元看作一刚性载体,并建立固连于测量单元的载体坐标系ObXbYbZb,如图1所示。

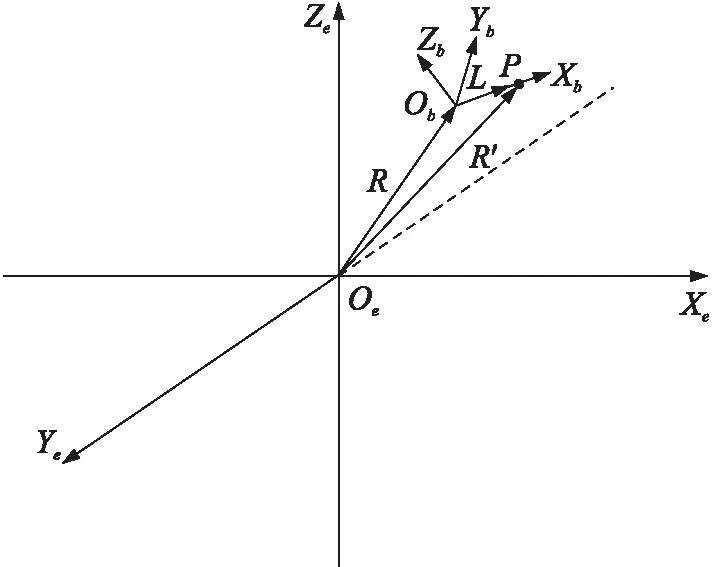
图1　载体系与惯性系的关系

载体非质心处的P点满足如下矢径方程:

R′=R+L

(1)

对式(1)两边二次求导,由哥氏定理可得:

(2)

由于:

代入式(2)得:

(3)

2　双路MEMS三轴加速度计的对称配置方案

基于上述无陀螺惯导原理,国内外出现了六加速度计、九加速度计等多种配置方案和相应的加速度解算方法,并提出了许多提高解算精度的途径[14-16]。但这些方法均针对大型飞行器、船舶等应用领域设计,使用的加速度计数量较多且空间布局复杂,并不适合小体积、低成本的手势测量设备。为了适应和满足手持式测量单元的设计要求,本文提出一种双路MEMS三轴加速度计的对称配置方案。该方案在保证测量单元体积小、易手持特征的同时,可实现手势原始特征的快速解算;由于手势特征测量的短时特点,解算算法的误差积累可控制在合理范围,可为进一步的手势识别提供依据。

在测量单元相对质心的对称位置安排两个MEMS三轴加速度模块,可构成双路共六轴加速度计配置方案,如图2所示。

图2　双路MEMS加速度计配置方案

ObXbYbZb为固连于测量单元的载体坐标系,坐标原点Ob所在位置为测量单元对应装置的质心,Xb与过质心的长轴方向一致;MEMS加速度传感器模块1和模块2被固定安装在Xb轴上坐标原点Ob两侧,传感器1和传感器2到原点的距离分别为l1和l2,且l1=l2≠0,即:传感器1和传感器2在Xb轴上关于原点Ob对称。为了随后解算质心加速度的方便,传感器1和传感器2的安装需保证Xb与传感器某一敏感轴重合,图2中为Xa轴,但不限于Xa轴。

使用上述配置方案设计手持式测量单元硬件时,可将两个加速度模块对称安装在手持装置的长轴位置,质心处可考虑安排具有射频接口的SOC芯片,从而保证狭长布局的手写笔形状,便于手持。

3　手势原始特征解算

手势原始特征指的是测量单元质心处的对地加速度。由于测量单元随手势运动过程中姿态可能发生变化,需通过两个加速度模块的比力输出依次解算出装置的旋转角速度、装置的姿态角(方向余弦矩阵),质心对地加速度。

3.1　质心对地加速度解算方程

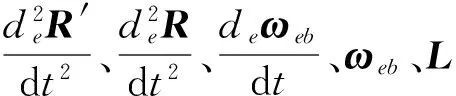
(4)

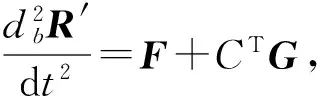
(5)

图2中,加速度传感器1和传感器2处均满足式(5),因此得下列方程组:

(6)

根据加速度计对称配置方案,取L1=[-l00]T,L2=[l00]T,并设I=[100]T,则由式(6)得:

(7)

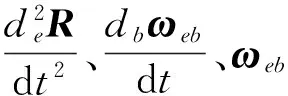
(8)

由于C和ω=[ωXωYωZ]T满足如下关系:

(9)

式(8)和式(9)联立构成手持装置质心对地加速度解算方程组:

(10)

在无陀螺惯性测量单元中,从两路加速度计输出解算旋转角速度是问题的关键。从式(10)可以看出,质心对地加速度的求解最终依赖旋转角速度ω的解算。

3.2　角速度的解算

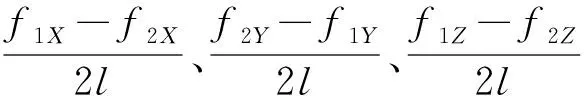
(11)

手势输入过程中,手写笔形状的测量单元基本不会发生绕长轴的旋转,根据图2中加速度计的布局特征可知,横滚角φ的变化很小。因此ωx≈0,式(11)可进一步简化为:

(12)

根据式(12)中第1式和第2式,可构造积分算法求解角速度分量ωY、ωz。

3.3　角速度解算的误差补偿

MEMS加速度计在实际测量中存在零漂和随机漂移,式(12)中的组合项cX、cY、cZ中包含综合误差,从而引起积分法求角速度的积累误差。虽然在空间手势特征提取应用中采样时长较短(如,数字的手写输入时间不超过3 s),积累误差有限,为提高测量精度,仍可根据式(12)中的冗余信息进行误差补偿。

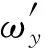
(13)

(14)

将式(12)中第3式两边求导得:

将式(12)中的第1、第2式,及式(13)代入上式得:

(15)

将式(14)与式(15)联立,可表示为如下矩阵形式:

(16)

在式(16)右端方阵非奇异时,可将εωy、εωz作为误差补偿量对积分过程中的ωY、ωz进行修正。

4　系统仿真实验

为了分析验证上述加速度计配置方案及对应角速度解算方法,假设测量单元旋转角速度和质心处线加速度满足以下模型:

其中,角速度单位为rad/s,加速度单位为m/s2。l1=l2=0.04 m,采样时长为2 s,采样间隔为5 ms,并假设二路加速度计的综合零漂为10-4gn,随机漂移为10-5gn。

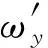
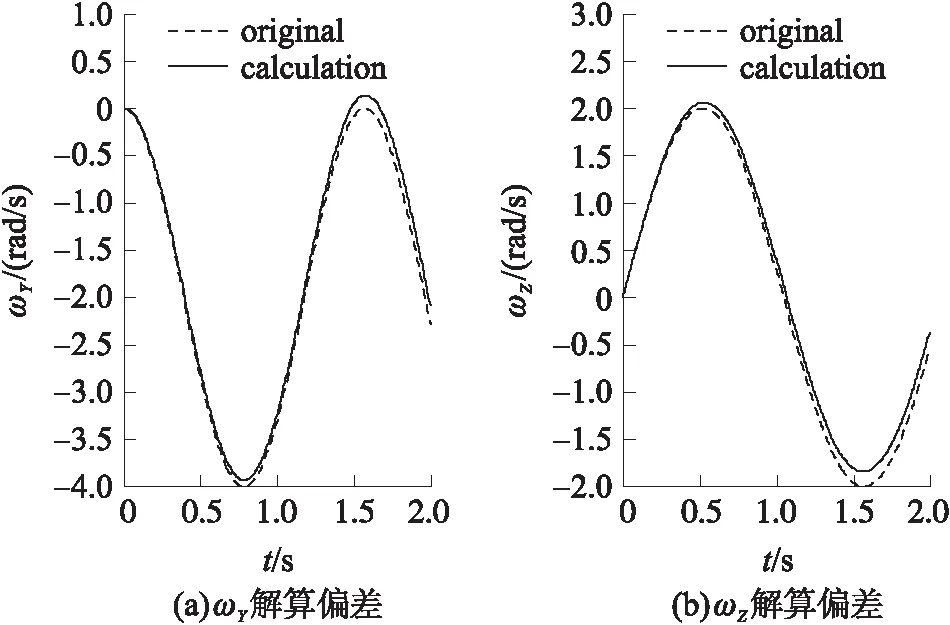
图3　无误差补偿解算偏差

图4　误差补偿后解算偏差

5　结论

本文讨论了一种用于三维空间手势输入的微惯性测量单元设计,包括两路三轴MEMS加速度计的对称配置方案及对应的角速度、线速度解算方法。两路加速度计在长轴方向上的对称放置,保证了测量单元的狭长几何特征和较小的体积,便于手持;同时,与该配置方案对应的角速度、线加速度解算方法的形式简单,在满足手势输入过程中横滚角变化不大条件下,可采用积分法求角速度;此外,由于手势输入的短采样时长特点,算法的积累误差控制在较小范围,利用角速度推导式中的冗余信息,可估计角速度的积累误差并进行补偿,从而进一步提高解算精度。

参考文献:

[1]Sushmita M,Tinku A.Gesture Recognition:A Survey[C]//IEEE Transactions on System,Man,And Cybernetics,2007,37(3):311-324.

[2]Jang I J,Park W B.Signal Processing of the Accelerometer for Gesture Awareness on Handheld Devices[C]//Proceedings of the IEEE International Workshop on Robot and Human Interactive Communication,2003:139-144.

[3]Kela J,Korpipaa P,Marca D.Accelerometr-Based Gesture Control

for a Design Environment[J].Personal and Ubiquitous Computing,2005,10(5):258-299.

[4]陈意,杨平,陈旭光.一种基于加速度特征提取的手势识别方法[J].传感技术学报,2012,25(8):1073-1078.

[5]李国峰,王锦,张勇,等.基于MEMS加速度传感器的智能输入系统[J].传感技术学报,2009,22(5):643-646.

[6]DiNapoli L D.The Measurement of Angular Velocities without the Use of Gyros[D].Philadelphia:The Moore School of Electrical Engineering,University of Pennsylvania,1965.

[7]Schuler A R.Measuring Rotational Motion with Linear Accelerometers[J].IEEE Trans on AES,1967,3(3):465-472.

[8]Merhav S J.A Nongyroscopic Inertial Measurement Unit[J].Journal of Guidance,Control,and Dynamics.1982,5(3):227-235.

[9]Lee Sou-Chen,LIU Cheng-Yu.An Innovative Estimation Method with Own-Ship Estimator for an All Accelerometer-Type Inertial Navigation System[J].International Journal of Systems Science,1999,30(12):1259-1266.

[10]史震,于秀萍.无陀螺捷联式惯性导航系统[M].哈尔滨:哈尔滨工程大学出版社,2005.

[11]岳鹏,史震.基于MEMS加速度计的无陀螺惯导系统[J].中国惯性技术学报,2011,19(2):152-156.

[12]薛洋,金连文.一种基于加速度传感器的虚拟手写数字特征提取及识别方法[J].模式识别与人工智能,2011,24(4):492-500.

[13]薛洋.基于单个加速度传感器的人体运动模式识别[D].华南理工大学,2011.

[14]Algrain M C.Accelerometer-Based Platform Stabilization[J].SPIE Acquisition,Tracking,and Pointing,1991,1482:367-382.

[15]Rios A.Real Time Data Smoothing to Improve the Performance of a Strapdown Nongyroscopie Attitude Propagation Inertial Unit[C]//Darmstadt,20-23,Oct,1986.

[16]王劲松,王祈,孙圣和.无陀螺微惯性测量组合的优化算法研究[J].哈尔滨工业大学学报,2002,34(5):632-635.

王祥雒(1977-),男,河南洛阳人,洛阳师范学院讲师,硕士,工程师,研究领域为机器学习、嵌入式微控制与传感技术、量子计算等,wx_25@aliyun.com;

杨春蕾(1980-),女,河南科技大学讲师,硕士,研究领域为数据库系统、脑电传感技术、智能控制等;

郑瑞娟(1980-),女,河南科技大学副教授,博士,主要研究方向为物联网应用,传感技术。