Design and Analysis of a Touch Mode Capacitive Microaccelerometer*

, ,

(1.College of Mechanical Engineering,Chongqing University of Technology,Chongqing 400054,China;2.College of Engineering and Technology,Southwest University,Chongqing 400044,China)

Accelerometer is one of the first devices demonstrated using MEMS technology.The wide spectrum of applications for MEMS accelerometers is attributed to their small size,high sensitivity and low cost.Although many physical effects can be used for acceleration sensing,the capacitive sensing mechanism is dominant due to capacitive MEMS accelerometer with high sensitivity,low power consumption,low noise level,stable DC characteristics and less temperature dependence.Furthermore,both surface and bulk micromachining can be used to fabricate a variety of capacitive accelerometers with performance ranging from the low-end automotive application grade to the high-precision inertial navigation grade[1-2].

So far,all the reported capacitive MEMS accelero-meter is operating in normal mode,that is,no-touch mode.It inherits the advantages of capacitive MEMS accelerometer.However its output is nonlinear with respect to input changes and the sensitivity in the near-linear region is not high enough to ignore the parasitic capacitance effects.In this paper,a novel touch mode capacitive microaccelerometer is developed to overcome the disadvantages of the classical counterparts.

Touch mode effect is the most important subject.It has a major effect on the overall performance of the touch mode sensor[3-4].By looking at MEMS devices,there have been good suggestions for solving the touch-down problems,but as of today none of the literatures has come up to a final analytical solution for calculating the touch down effect.That is to say,the effect of touch mode has not been evaluated efficiently[5-6].A simulation solution is one of the valuable processing for design a sensor,but it is very time consuming to optimize the sensor’s parameters such as the radius,cavity depth,diaphragm and dielectric thickness.Therefore,in this paper,it is aimed to design,obtain analytical solution for the diaphragm of the sensor deflection before and after touch point.A simple analytical solution is presented to model the flexion of a circular diaphragm with clamped edges under the load,where the touch down effect and the evolution of touch radius are considered.

Fig.1　Cross-sectional view of touch mode capacitive microaccelerometer

1　Design

Fig.1 presents a cross-sectional view of a touch mode capacitive microaccelerometer[7].It is composed of a proof-mass suspended by four microbeams,two circular deformable diaphragms with clamped edges served as movable electrodes,and two fixed electrodes buried under the corresponding dielectric.tandhare the thickness of dielectric and the movable electrode respectively.gis cavity depth.The deformation of the two circular diaphragms in response to acceleration results in the variance of capacitance,which can be measured with an interface circuit.In normal mode operation,the deformable diaphragm is kept distance away from top/bottom fixed electrode.In touch mode operation,when external acceleration increases,the circular diaphragm will deflect and start touching the top/bottom fixed electrode with a distance of insulator in between.The concept of parallel plate capacitor is expressed by Eq.(1).

C=(ε0εrA)/d

(1)

whereε0is the permittivity of the media between diaphragms,εris the dielectric constant of the insulating diaphragm material,Ais the area of the electrode,anddis the distance between the movable electrode and the corresponding fixed electrode.

The concept of the capacitance element of the sensor requires a change in the capacitance as a function of some applied acceleration load.A realization function of this concept would be the electrodes of the capacitor could move under acceleration load,for example,if the electrodes move closer together,the cavity depth,g,would decrease,resulting an increase in capacitance of the sensor.In touch mode,when external acceleration increases on the diaphragm,the touched radius(r1)will increase,and at the same time the untouched radius(r2)will decrease,therefore the value of capacitance will increases nearly linearly with increasing acceleration,before touch point the radius(r1)is zero.As shown in Fig.2,R,r1,r2are radius of the movable electrode,touched-point radius,and untouched-point radius respectively.

Fig.2　Simplified mechanical model of the deformable diaphragm

2　Model

2.1　Simplified Mechanical Model

The principle of the paper is to obtain analytical solution for a circular diaphragm with clamped edges deflection before and after touch point[8-10].Considering the symmetry of the microstructure,the simplified mechanical model of the movable diaphragm is shown in Fig.2,wherePis an applied acceleration load,and given by Eq.(2).

P=ma

(2)

wheremis the mass of the proof-mass,ais an applied acceleration.

2.2　Small Deflection Model

A diaphragm is defined as thin diaphragm or small deflection if the gap between two electrodes is less than 1/5 of diaphragm’s thickness,and the strains and mid-plane slopes are much smaller than unity.Based on small deflection theory for circular diaphragm with clamped edges,the deflectionwof any point on a circular diaphragm under acceleration load is expressed by Eq.(3)[11].

(3)

whereris the radial distance from the center,Dis the flexural rigidity of the diaphragm and given by Eq.(4).

D=Eh3/[12(1-ν2)]

(4)

whereEis Young’s Modulus andνis the Poison’s ratio.

Eq.(3)gives the deflectionw(r)before touch of the circular diaphragm as a function of radius,which is valid before the movable diaphragm touches the fixed electrode(with the insulator in between the diaphragms).Furthermore,the maximum deflection is located in the center point of the diaphragm(r=0),and defined by Eq.(5).

wmax=w0=PR2/(16πD)

(5)

2.3　Large Deflection Model

A diaphragm defined as of thick diaphragm or large deflection if its deflection is up three times larger than diaphragm’s thickness.For this situation,it is needed to consider the radial displacement as well as the lateral displacement of elements on the diaphragm.The following equations are proposed to describe the energy of the system[11].

(6)

(7)

whereVandV1represent,respectively,the flexural and deformation energies.εrandεtare the radial and transversal strains described by Eq.(8).

(8)

wherewis the transversal deflection anduis the radial displacement.

3　Analytical Analysis before and afterTouch-Mode Effect

Small deflection model is built on simple assumptions.So in this paper,large deflection model for circular diaphragm with clamped edges is taken into account.Let us consider that transversal deflectionwcould be described by Eq.(3),that is

(9)

Therefore,the flexural energy

(10)

Let us suppose that the radial displacementucould be described by the following Eq.(11).

u=r(R-r)(C1+C2r+C3r2+…)

(11)

If we take into account only the two first terms of the power series,then deformation energy,then

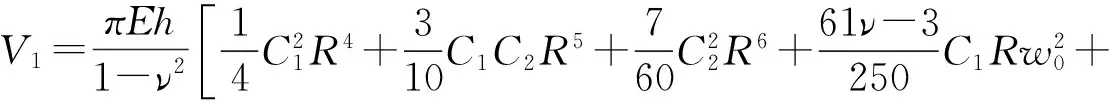
(12)

Consider the diaphragm at equilibrium to be at minimum energy,that is

(13)

we can findC1andC2

(14)

So deformation energy can be calculated.When the Poison’s ratioν=0.3,

(15)

Therefore,total energy of the system

(16)

The last step is to apply function principle to obtain the large deflection solution.Based on the following Eq.(17)

(17)

then we obtain the maximum deflection

(18)

It is obvious that the maximum deflectionw0based on large deflection model is not proportinal to the acceleration loadP.The 2nd factor reflect the influence of tension in middle-plane on the maximum deflection.

Now we discuss the touch mode.The modeling of contact behavior of the diaphragm is a much more difficult problem to solve.A pseudo spectral method(PSM)is used to solve the nonlinear differential equations that govern the deflection of a diaphragm.The other method is to evaluate the deflection profile applying the principle of virtual works to balance the flexural and deformation energies calculated when the sensor goes in touch mode.In addition,finite elements method(FEM)is widely used to model touch mode sensors,but it is very time consuming to optimize the sensor’s parameters such as cavity depth,diaphragm and dielectric thickness.The other proposed technique is to divide the contact area into small elements,cutting the diaphragm going beyond the electrode plane by using deflection theory,and computing different contributions to capacitance based on the approximation of parallel plates for each element.But an empirical function should be incorporated in the model to correct the nonlinearities for which the contact is taking place.Furthermore,while this model can give satisfactory results,the empirical function to correct the profile of the diaphragm has no theoretical meaning and its discreet nature makes it more of a simplified finite elements technique than an analytical one.Therefore,a simple analytical model is very attractive for the optimization of touch mode capacitive sensor.

In this work,the modeling of touch mode is realized using a method proposed by Ko et.al[12].We already know that the solution for large deflections is valid until the diaphragm first touches the fixed electrode.Beyond this load or the critical acceleration,the model is no longer useful.However,for every load(acceleration),we can find the radius of a virtual diaphragm that just barely contacts the bottom,this is untouched-point radiusr2mentioned above.The difference between the actual diaphragm radiusRandr2gives the touched-point radiusr1.That is,r1before touch is equal to zero and touch point accelerationacris given by Eq.(18)

(19)

Therefore,the equivalent untouched radiusr2of a virtual circular diaphragm by using Eq.(19),and is defined byw0=g,R=r2.When acceleration loadais lager thanacr,

(20)

Touched-point radiusr1is given by Eq.(21).

r1=R-r2

(21)

4　Summary

Touch mode effect is the most important subject for the touch mode sensor.By looking at MEMS devices,there have been good suggestions for solving the touch-down problems,but as of today none of the literatures has come up to a final analytical solution for calculating the touch down effect.In this paper,a novel touch mode capacitive microaccelerometer is developed.A simple analytical solution is presented to model the flexion of the circular diaphragm with clamped edges before and after touch point under the load,where the touch down effect and the evolution of touch radius are considered.

[1]Navid Yazdi,Farrokh Ayazi,Khalil Najafi.Micromachined Inertial Sensors[J].Proceedings of the IEEE,1998,86:1640-1659.

[2]Dong Yonggui.Microsensor[M].Beijing:Tsinghua University Press,2007:231-236.

[3]Lv Haojie,Guo Qiang,Hu Guoqing,A Touch Mode Capacitive Pressure Sensor with Long Linear Range and High Sensitivity[C]//Proceedings of the 3rd IEEE Int Conf on Nano/Micro Engineered and Molecular Systems,2008:796-800.

[4]Giulio Fragiacomo,Thomas Pedersen,Ole Hansen,et al.Intrinsic Low Hysteresis Touch Mode Capacitive Pressure Sensor[C]//IEEE Sensors Conference,2010:2279-2282.

[5]Hezarjaribi Y,Hamidon M N,Sidek R M,et al.Analytical and Simulation Evaluation for Diaphragm’s Deflection and its Applications to Touch Mode MEMS Capacitive Pressure Sensors[J].Australian Journal of Basic and Applied Sciences,2009(4):4281-4292.

[6]Yadollah Hezarjaribi,Mohd Hamidon,Roslina Sidek,et al.Evaluation for Diaphragm’s Deflection for Touch Mode MEMS Pressure Sensors[J].The International Arab Journal of Information Technology,2011(2):141-146.

[7]Liu Yu,Mi Lin,Wang Guochao,et al.A Touch Mode Capacitive Microaccelerometer[P].China Patent,201110341475.3.2013.

[8]He Xiaoting,Wu Jianliang,Zheng Zhoulian,et al.Axisymmetrical Deformation of Prestressed Circular Membrane under Uniformly Distributed Loads[J].Journal of Chongqing University,2010(1):109-112.

[9]Chen Shanlin,Zheng Zhoulian.Large Deflection of Circular Membrane under Concentrated Force[J].Applied Mathematics and Mechanics,2003(1):25-28.

[10]Jin Congrui.Large Deflection of Circular Membrane under Concentrated Force[J].Applied Mathematics and Mechanics,2008(7):806-812.

[11]Timoshenko S.Theory of Plates and Shells[M].Beijing:Science Press,1977:72.

[12]Ko W H,Wang Q.Touch Mode Capacitive Pressure Sensors[J].Sens Actuators,1999,75:242-251.

刘妤(1974-),女,四川泸州人,副教授,博士。现从事微传感器、机械工程等方面的研究,liuyu_cq@126.com。