一种结构解耦的新型应变式三维力传感器研究

张海霞,崔建伟,陈丹凤,陈杨洋

(东南大学仪器科学与工程学院,南京 210096)

传感器在现代科学技术中的重要性已经越来越被认可。无论是在工业与国防领域,还是在生物工程、医疗卫生、环境保护等领域,处处都离不开传感器的应用[1]。多维力传感器是实现机器人类化和智能化最为重要的一种传感器,它是工程力学检测和机器人运动控制的基础,其应用范围也越来越广泛[2]。

多维力传感器在结构形式上主要有筒式、柱式、环式、悬臂梁式、十字梁式、倒T型等形式[3-6]。目前,应变式多维力传感器,其存在的缺点是维间耦合误差较大[7],结构复杂,标定困难[8],限制了它的推广应用。在多维力传感器的实际应用中,很多场合要求维间耦合误差小、测量精度高、结构简单的测力传感器[9],如航天员在模拟太空环境中进行舱外攀爬活动训练时,用于测量航天员左右手臂的测力装置[10]。为此,本文对传统应变式三维力传感器结构进行优化,提出了一种新型三维力传感器结构。该传感器可以感应三维空间坐标系下x、z方向的力Fx、Fz和y方向的力矩My,并且自身结构具有解耦功能,测量精度高,维间耦合误差小。另外,其结构简单,制造方便,可大大降低加工成本。

1　传感器的结构设计

1.1　三维力传感器的结构

新型三维力传感器结构如图1所示[11]。

图1　新型三维力传感器结构

在矩形截面梁上开通孔和通槽后,使得其壁厚不一致,从而矩形截面梁就变成了应变梁。应变梁壁厚最薄处是其最敏感的位置。它实际上包含了两组二维力传感器,或者是4个一维力传感器,因此这些传感器用横梁连接后形成的传感器可以看作4个简单一维力传感器A1、A2、B1、B2的线性叠加。

图2　弹性体的应变原理

1.2　应变片布片原理

根据本文图1所给的坐标轴,当受到载荷Fx、Fz、My,它将在应变梁上产生形变,并使应变梁上的应变片电阻发生变化,电桥的平衡被打破,在输出电压端有电压输出。

梁在正弯矩作用下发生弯曲变形,必然引起内侧纵向线段缩短,外侧纵向线段伸长,中间必有一层纵向线段长度不变的中性层。取任意梁横截面的对称轴为轴y,中性轴(中性层与横截面的交线)为轴z,轴x沿梁的轴线方向,如图2(a)。变形后,中性层纵向线段的圆弧线曲率半径为ρ,微段dx两端横截面绕其中性轴相对地转动了一个角度dθ。由原长dx=ρdθ,变为(ρ-y)dθ。因此,距中性层为y的任一纵向线段ab的纵向应变为

因此,将一对应变片分别贴在变形位置的受拉区和受压区,可以感应弹性体的形变;再通过两组应变片组成惠斯通全桥电路,可以测量应变大小。根据本弹性体结构,将各应变片位置分配如下:

16片应变片的分布如图3所示,图中Ri/Rj所示,Ri贴于正面,Rj贴于背面。

图3　各应变片的位置分配

图4　应变及电压输出电路

1.3　三维力的测量方法

每个一维力传感器的应变区域都贴有4片应变片,共16个应变片组成4个惠斯通全桥电路,得到4路电压信号如图4所示。其中桥路1和桥路2用于测量Z方向的力Fz,在力Fz作用下,桥路1和桥路2各自有两个应变片处于负应力区(压应力),另外两个应变片处于正应力区(拉应力)。由于应变片的压阻效应,阻值变化通过2个惠斯通电桥分别转化为电压信号,通过将两个桥路的输出电压值叠加,就可以得到相应的力值,从而实现力与电的转化。同理,桥路3与桥路4用于测量X方向的力Fx。在X或Z方向力作用下,总有两个桥路,且每个桥路中有两个应变片是处于拉应变,另两个应变片处于压应变(两正两负),其余两个桥路的应变片敏感方向与力的方向垂直,理论上整个桥路中的应变输出能够正负相抵,即对Y方向的力不敏感。力矩My也是通过测量桥路1和桥路2的电压输出变化,由于采用不同的组桥方式,使得力/力矩Fz/My的测量相互独立,互不影响。

ΔU1、ΔU2、ΔU3、ΔU4分别对应于桥路1、桥路2、桥路3、桥路4的输出信号。根据传感器的结构,将桥路1与桥路2的输出信号求和,该信号对Z轴方向力信号敏感;将桥路3与桥路4的输出信号求和,得到的信号对X轴方向力信号敏感;将桥路1与桥路2的输出信号做差,得到的信号对Y轴方向的力矩信号敏感。测量方式可以表示为,

(1)

式中,ΔUFx、ΔUFz、ΔUMy代表了平面力系坐标下受力所产生的电压信号变化量。根据材料力学原理,设16个应变片R1,R2,R3,…,R16的应变输出分别为s1,s2,s3,…,s16,则输出电压信号变化量可以表示为,

(2)

式中,K1、K2、K3分别是ΔUFx、ΔUFz、ΔUMy的输出系数。

2　有限元仿真

本文采用ANSYS软件对弹性体进行有限元静态分析,确定其结构尺寸以及应变片的黏贴位置。

2.1　模型的建立

在利用ANSYS进行建模时,采用软件自带的自顶向下的实体建模方法,好处是利于网格精度划分的控制。弹性体的结构尺寸如表1所示。

表1　弹性体的结构参数　mm

弹性体的加工材料硬铝合金LY12的参数如表2所示。

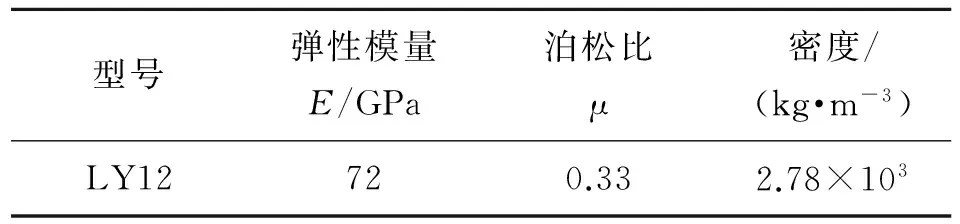
表2　LY12的材料参数

在ANSYS分析建模时,分析单元采用3D实体单元SOLID95,该单元有20个节点,每个节点有3个自由度。在有限元分析中,需将实体单元进行网络划分得到有限元模型。划分网格时应从网格数量、网格疏密等方面考虑。本文采用在Global-Size里设置单元尺寸、自由网格划分的方式对弹性体进行网格划分,然后再对其应变敏感区域进一步细化,得到的有限元模型如图5所示,共有285 256个节点,180 431个单元。

图5　弹性体有限元模型

2.2　加载和求解

根据传感器的安装固定方式对该传感器弹性体底面两端分别施加面约束,各方向自由度设为零。在横梁顶部端面中心施加满量程集中力载荷Fx、Fz,在横梁端面中心距离为L1的两个端点处施加一对力偶。求解后,传感器应变梁变形如图6所示。

3　计算结果分析

3.1　应变分析

图6从左到右分别是3种受力情况下的应变分布。

图6　弹性梁的应变分布

(a)当施加Fx=200 N作用时,弹性体向X方向倾斜,梁的弯曲变形主要集中在B1、B2两个一维力传感器部分,且B1、B2的应变相同。B1孔壁外,6、7处受拉,5、8处受压。考虑到应变片的贴片,应分析应变片的轴向方向应变,即Y方向的应变。

(b)当施加Fz=200 N作用时,弹性体向Z方向倾斜,梁的弯曲变形主要集中在A1、A2两个一维力传感器部分,A1、A2的应变相同。A1孔壁外,1、4处受拉,2、3处受压,分析应变片轴向Y方向的应变。

图7　沿路径各节点应变分布趋势

(c)当施加力矩My=19 N·m作用时,弹性体逆时针旋转,梁的弯曲变形主要集中在A1、A2两个一维力传感器部分,但A1、A2的应变相反。A1孔壁外,1、4处受拉,2、3处受压,A2孔壁外,10、11处受拉,9、12处受压,分析应变片轴向Y方向的应变。

由应变图6显示可知,对于每种受力情况,在My=19 N·m时产生的最大应变ε=1.184×10-3,ε×E=(1.184×10-3)×72 GPa≈85.248 MPa,小于硬铝合金的屈服强度360 MPa[12],安全系数为4.2,说明安全。

弹性体属于敏感元件,为了获得较高的灵敏度和稳定性,需要选择最佳的贴片位置。为分析节点应变大小的关系,利用ANSYS后处理器提供的路径映射技术,它是基于插值运算的处理技术,能够映射任何结果数据到模型的任何路径上。

本文选择位于发生弯曲变形的应变梁侧面沿中心线的位置定义路径,如图5所示。得到路径上各节点的应变如图7所示。其中横坐标表示路径距中心线原点各点的坐标值,单位为cm,纵坐标为对应Y方向的应变值。三维力的满量程为200 N,三维力矩的满量程为19 N·m。

如图7所示,在单维力Fx=200 N作用下,路径二区间在5 mm与30 mm处的应变最大,可以确定3 mm～7 mm和28 mm～32 mm区域为B1、B2两个一维力传感器应变片的贴片区域。在单维力Fz=200 N作用下,路径一区间在20 mm与45 mm处的应变最大,可以确定17 mm～21 mm与43 mm～47 mm区域为A1、A2两个一维力传感器应变片的贴片区域。

3.2　维间耦合分析

在力Fx、Fz和力矩My作用下,16个应变片应变输出如表3所示。

注:表中正值代表拉应变,负值代表压应变

通过结构静力分析发现,X方向的力主要影响桥路3的4个应变片和桥路4的4个应变片,其他位置的桥路对Fx不敏感。Z方向的力主要影响桥路1和桥路2的所有应变片,桥路3和桥路4的应变片对其不敏感。Y方向的力矩对桥路1和桥路2有影响,对桥路3和桥路4不敏感。我们取桥路3和桥路4应变输出之和作为一路信号εx,标志力Fx;桥路1与桥路2的应变输出之和作为一路信号εz,标志力Fz;桥路1与桥路2的应变输出之差作为一路信号εy,标志力矩My。三路信号之间具有互相独立,互不影响的特点。

将表3的应变输出值代入式(2),桥路电压信号变化量和传感器受力的关系可以表示为:

(3)

假设弹性体的变形与惠斯通全桥电路的输出为线性,测量矩阵可以将式(3)标准化得公式[13](4),

(4)

(5)

维间耦合误差是指某方向分量未施加力/力矩时,由于其他方向分量上施加了力/力矩而对该分量产生的干扰。由文中式(5)近似对角矩阵表明,该传感器的结构能够实现自解耦。理论上,式(5)应该是理想的对角矩阵,但由于维间耦合干扰,未施加分量方向上有微小应变输出。因此,式(5)矩阵中每一行所有未施加分量方向上的微小应变输出矢量和,即为对应方向的维间耦合误差。计算公式如下:

由上所述计算公式可以看出,该应变式三维力传感器的最大维间耦合误差为0.4%F.S.。

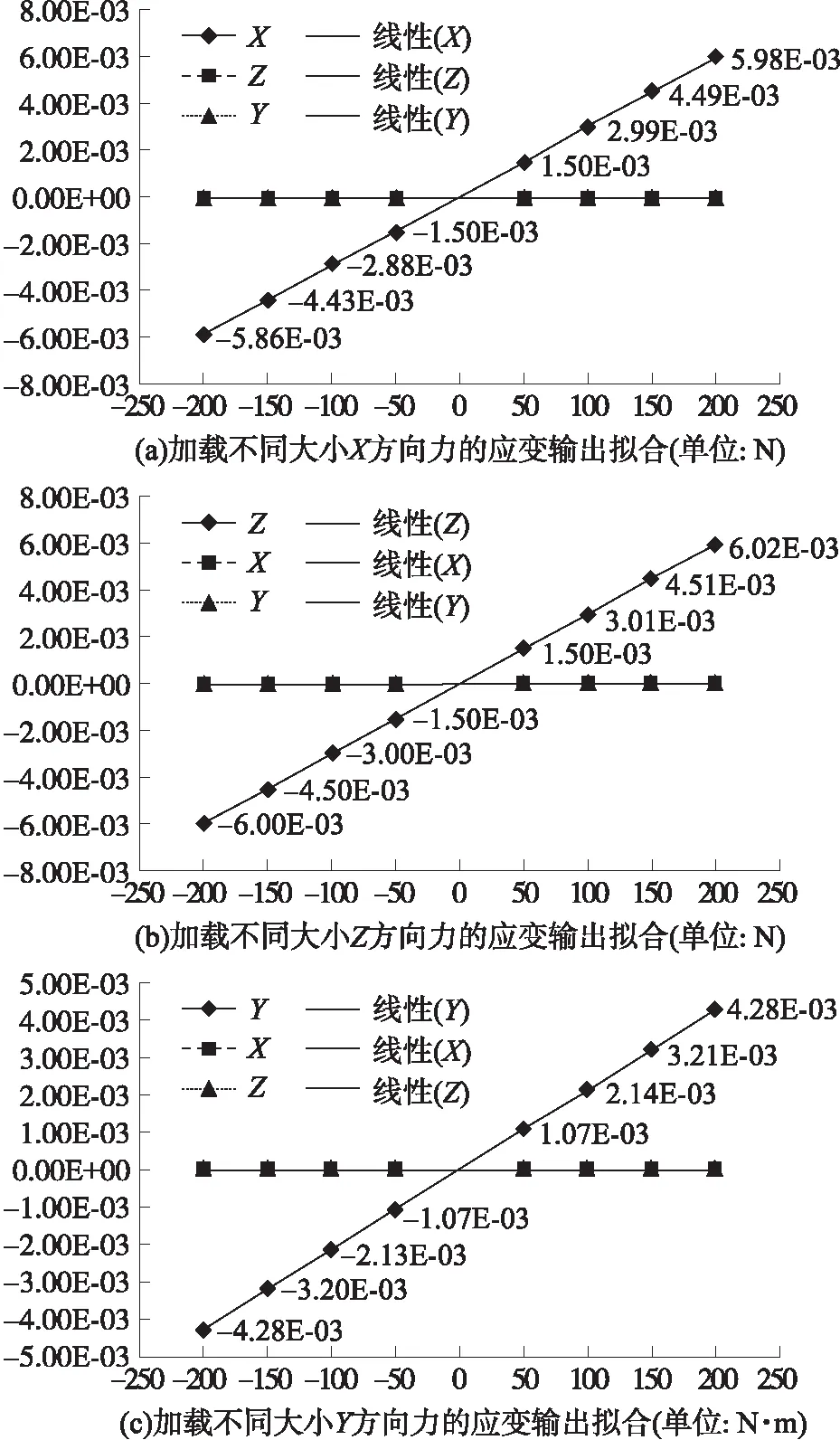
图8　加载不同大小力/力矩的应变输出

仿真分析计算得出新型传感器结构解耦的前提条件是该传感器结构是线性的,因此,本文对其线性度进行了分析。将加载不同力/力矩时的应变片输出代入式(2)(计算不带输出系数的总应变),通过拟合得到直线,如图8所示。

从图8可以看出,3个方向分别加载不同大小力/力矩时,新型传感器结构的弹性变形都呈线性输出,未施加力/力矩分量方向上的干扰趋近与零。由此表明:该传感器弹性体自身结构线性度好,具有解耦功能,且有限元分析结果证明了其自解耦性能的优越性。

4　结束语

本文设计了一种结构简单、制造方便的三维力传感器,用于测量Fx,Fz,My3个维度的广义力。通过对传感器的弹性体进行有限元分析,精确地掌握了弹性体各部分的受力情况,得到弹性体的应变数据。利用后处理器中的路径映射技术,确定弹性体应变梁表面的最佳贴片位置。

通过计算得出该应变式三维力传感器的最大维间耦合误差为0.4%F.S.,与其他应变式多维力传感器的最大维间干扰误差为1.14%F.S.[13]、3.56%F.S.[14]等相比,该传感器维间耦合误差大大减小。在今后的工作中,我们将完善传感器装配结构的设计,进行传感器标定实验并进行进一步研究。

参考文献:

[1]吴强,俞志伟.一种小型电阻应变式三维力传感器的仿真设计[J].中国机械工程,2011,22(11):1289-1293.

[2]干方建,刘正士,任传胜.一种应变式多维力传感器的优化设计[J].传感器与微系统,2007,26(1):57-59.

[3]Joo J W,Na K S,Kang D I.Design and Evaluation of A Six Component Load Cell[J].Measurement,2002,32(2):125-133.

[4]Li Yingjun,Zhang Jun,Jia Zhenyuan.A Novel Piezoelectric 6-Component Heavy Force/Moment Sensor for Huge Heavy-Load Manipulator’s Gripper[J].Mechanical Systems and Signal Processing,2009,23(5):1644-1651.

[5]Gab Soon Kim.Design of a Six-Axis Wrist Force/Moment Sensor Using FEM and Its Fabrication for an Intelligent Robot[J].Sensors and Actuators A:Physical,2007,133(1):27-34.

[6]张正杰,吉爱红,王周义,等.用于壁虎脚掌接触力测试的3-维传感器[J].传感技术学报,2007,20(6):1271-1274.

[7]吴宝元,申飞,吴仲城.应变式多维力传感器结构优化设计方法研究[J].传感技术学报,2010,23(10):1412-1416.

[8]曹效英,秦岗,宋爱国.ANSYS在腕力传感器结构设计中的应用[J].传感技术学报,2005,18(2):414-417.

[9]俞志伟,宫俊,吴强,等.小型三维力传感器的设计和解耦测试研究[J].传感技术学报,2012,25(1):38-43.

[10]宋爱国,马俊青,茅晨,等.航天员舱外攀爬活动训练用的四维抓取力的测力装置[P].中国发明专利,CN202582805U,2012.

[11]崔建伟,宋爱国,宋钰涛.一种三维力传感器[P].中国发明专利,CN202255706U,2012.

[12]茅晨,宋爱国.新型六维腕力传感器[J].南京信息工程大学学报(自然科学版),2011,3(5):402-407.

[13]Song Aigu,Wu Juan,Qin Gang,et al.A Novel Self-Decoupled Four Degree-of-Freedom Wrist Force/Torque Sensor[J].Measurement,2007,40(9-10):883-891.

[14]陈乐.三维力传感器的设计[J].江苏省计量学术论文集,2008,111-115.

张海霞(1986-),女,江苏盐城人,硕士研究生,主要研究方向为多维力传感器技术,zhanghaixia1128@sina.com;

崔建伟(1969-),男,山西长治人,博士,副教授,主要从事机器人传感技术方面的研究,cjw@seu.edu.cn。