基于迭代学习控制的列车自动运行研究

王 娟，李国宁，刘雨佳

WANG Juan,LI Guoning,LIU Yujia

兰州交通大学 自动化与电气工程学院，兰州 730070

School of Automation and Electrical Engineering,Lanzhou Jiaotong University,Lanzhou 730070,China

1 引言

列车自动运行（ATO）系统是列车自动控制（ATC）系统中替代司机并对列车进行自动控制的智能子系统，其功能包括列车的自动启动、自动调速、自动停车和定点停车等，其控制目标是在有限时间区间内对给定的目标速度曲线进行完全跟踪。当所有列车均能严格跟踪各自的速度曲线行驶时，超速和追尾事故自然不会发生，同时还可以满足列车运行的高效、准时、舒适及节能的要求。

然而，高性能的列车控制系统必然依赖精确的动力学模型。由于列车的动力学特性非常复杂，难以建立精确的数学模型。同时，列车速度在运行过程中会受到线路坡度、风速及临时限速信息等多种因素的影响，这就限制了所有基于模型的控制方法的应用[1]。早期的经典控制算法在控制列车速度时，档位切换次数过多，舒适度差。而改进后的PID算法控制模式单一，当线路情况复杂时，难以达到理想的控制效果。20世纪80年代，一些学者尝试将专家系统、模糊控制、神经网络控制等智能控制算法引入到ATO系统的研究中。文献[2]中列举的有关列车自动运行智能控制算法的研究大都经过了实际系统的检验，但在这些研究成果中，也分别存在着专家知识获取困难、难以在线调整、搜索速度慢等缺点[3]。同时，列车运行的重复性这一典型特性没有被加以利用，隐含在列车重复运行过程中的大量有用信息被忽略了。而用迭代学习控制（Iterative Learning Control，ILC）来设计ATO系统需要较少的先验知识，本质上是一种无模型的控制方法，非常适用于像列车速度控制这种非线性控制系统。与其他智能控制方法相比较，迭代学习控制能够不断地学习和积累“控制经验”，并且不需要总结人工经验向控制器移植，有效克服了现有控制方法的不足。同时随着迭代次数的增加，控制精度和稳定性不断提高，保证列车的安全运行。

图1 基于迭代学习控制的ATO系统原理图

2 迭代学习算法的基本原理

迭代学习算法就是对于一个重复运行的动态系统，在有限时间间隔[0，T]内，给定一个理想输出 yd(t)，寻找一个学习机制，使得系统经过对期望输出 yd(t)的多次重复学习后，找到与输出 yd(t)相对应的理想输入ud(t)，使期望输出与实际输出间的误差满足系统精度的要求[4]。

基于迭代学习控制的列车自动运行研究，其根本目的就是通过设计合理的跟踪算法，将跟踪偏差控制在较小的范围内，指导列车严格跟踪目标速度曲线行驶，减少人工操纵列车造成的不必要能耗，提高列车运行的安全性与舒适性。同时，迭代学习算法具备很强的自学习能力，运算速度快，能够实时调节参数并进行优化。图1所示为基于迭代学习控制的ATO系统原理图。其中，迭代学习控制器包含两个部分，即系统未知参数的辨识和迭代学习控制律的设计。未知参数的辨识是指对于线路参数不完全或者控制经验不足的新建线路，为达到良好的控制效果，利用迭代学习方法对列车动力学模型的未知参数进行辨识。而对于已知较多参数的线路进行参数辨识能够实时调整参数，进一步地提高控制效果。

3 列车动力学模型的参数辨识

学术界对列车动力学模型的研究有一百多年的历史，其中最常用的列车动力学模型即Davis模型[5]如式（1）所示：

其中，t表示时间，单位是h；s代表位移，单位是km；v代表速度，单位是km/h；u代表列车牵引力或制动力，w(v)代表作用在单位质量上的基本阻力，g(s)代表作用在单位质量上的附加阻力，单位都是km/h2；l为一常数；a(s)代表位移s处坡道的坡度角。值得注意的是，普通坡道坡度角可以通过线路设计图纸得到，而弯道和隧道的折算坡度角却难以计算，因此需要把g当做一个时变参数 g(t)进行辨识，加上基本阻力系数a、b、c，共四个参数需要辨识。

在列车运行过程中，列车的位移、速度、列车的牵引力和制动力等信息可以通过车载仪器记录下来。为了便于求解，将式（1）化为标准的向量形式，同时考虑到列车实际运行过程中存在负载扰动φ(t)和测量噪声 μ(t)，迭代学习辨识模型应更精确地改写如下：

其中，各参量定义如下：

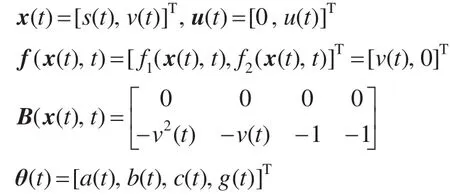
其中，k(k=0，1…)为迭代次数。在时间 t∈[0，T]内，ud(t)是实际运行时的输入量，其值在迭代辨识过程中是保持不变的。虽然负载扰动φ(t)和测量噪声 μ(t)是实际运行中产生且都是未知的，但它们不是在迭代运算过程中产生的，故与迭代无关。在对参数进行辨识的过程中，把ud(t)作为已知量，θk(t)作为控制量，那么 x(t)与θ(t)之间存在对应关系。因此，首先选定一个θ(t)的初始值，通过迭代使输出值逼近值 yd(t)，从而得到真实值θd(t)。假设待辨识参数θ(t)的初始估计值为θ0(t)，将其代入参数的迭代学习辨识公式，即

在式（3）中，A为4×2的学习矩阵，ek(t)为测量输出误差，则

同时还需要定义系统第k次迭代的状态误差Δxk(t)和参数误差Δθk(t)：

在文献[6]中已证明，随着迭代次数k→∞，当增益矩阵A满足时，输出量yk(t)将趋向实际测量值 yd(t)，待测参数θk(t)将趋向真实值θd(t)，即当辨识器中的学习增益满足收敛性条件时，待辨识参数可以随迭代过程收敛至期望值。综上所述，基于迭代学习算法的列车动力学模型未知参数辨识流程图如图2所示。

图2 未知参数辨识流程图

从图2可知，首先通过车载记录仪器得到ATO系统在有限区间上的一组历史输入输出数据，估计待辨识参数的初始值。然后，保持实测输入值不变，以实测输出值为跟踪目标，将估计值代入系统动力学方程式，得到输出的计算值。最后用该计算值减去实际输出值，判断输出误差是否满足迭代停止条件，若满足则参数辨识完毕，若不满足则重新估计参数值并代入迭代学习辨识器进行迭代辨识。

4 列车自动运行速度控制设计

4.1 迭代学习控制律的设计

迭代学习算法的核心是学习律（也叫控制律）的设计，是指以输出误差信号的累加构成控制输入信号。将迭代学习控制引入列车自动运行系统，选取作用在列车上的控制力（牵引力或控制力）为系统输入。但由于列车每次运行时的载重并不相同，会影响到系统的动态特性并不是完全重复，因此选取作用在列车单位质量上的控制力u(t)为系统输入。控制目标是使速度vk(t)及位移sk(t)在列车重复运行过程中能渐进跟踪上各自的期望曲线vd(t)和sd(t)。在对运行曲线控制律的设计上仍然沿用前文给出的列车动力学模型，即如式（6）所示：

式中各量表示意义与前文一致，而ωk(t)为系统所受的外部扰动，即φ(t)和 μ(t)之和，与迭代无关。为保证控制系统的稳定性和快速收敛性，假设基本阻力w(v(t))和附加阻力g(s(t))满足Lipschitz条件（证明见文献[6]），并且为了使每次迭代过程的初始状态完全重复，设定初始制动位移sk(0)为期望值sd(0)，初始速度vk(0)为期望值vd(0)。则可以通过学习律计算出新的输入信号uk+1(t)，即

其中，Δvk(t)=vd(t)-vk(t)，γ为学习增益。采用这种学习律，收敛条件如定理1所示[7]。

定理1对于式（6）描述的列车运行系统，在满足上述假设的条件下，采用式（7）给出的迭代学习律，若学习增益γ满足，当迭代次数趋向无穷的时候，系统的速度跟踪误差和位移跟踪误差可以收敛至0，即。

4.2 迭代控制系统结构原理

按照式（7）设计的迭代学习律，基于ILC的列车自动运行控制系统结构如图3所示。

图3中，Δvk(t)表示期望速度轨迹vd(t)与上次运行输出vk(t)的误差，Δvk+1(t)表示期望速度轨迹vd(t)与本次运行输出vk+1(t)的误差，xk(t)和xk+1(t)为系统上次和当前输出的状态向量，ωk(t)和ωk+1(t)为系统上次和当前输出所受的外部干扰。系统第k+1次迭代学习的控制输入uk+1(t)是由第i次控制输入uk(t)以及系统前次速度误差Δvk(t)通过迭代学习而得到的，因此该算法能够及时调整输入控制力的大小，保证系统的平稳性和高精度，避免了多次切换牵引力与制动力而造成的能耗。

图3 基于ILC的列车自动运行控制系统结构

5 仿真实验

为验证基于迭代学习控制算法对列车速度跟踪控制的有效性，本文利用MATLAB软件对列车运行速度曲线进行跟踪仿真实验。结合参考文献[8]，在仿真中，选取一段长为34 km，其中包含一段坡度为12'，长为10.54 km的上坡道，线路的纵剖面图如图4所示。

图4 线路的纵剖面图

5.1 未知参数的辨识仿真

为了能够快速准确地辨识未知参数，选取图4中第一段长为11.4 km的线路。该线路没有坡道，并且在350 s内完成运行。在这段时间内期望速度输出vd(t)、期望位置输出sd(t)和控制输入ud(t)分别为：

由文献[9]可知，当列车运行于平道时，附加阻力为零。当列车完全在坡道上运行时，附加阻力为该处坡度角的正弦值，即为一常数。当列车在平道与坡道的结合部运行时，附加阻力近似为位移的线性函数。由于此处仿真所选取的线路没有坡度，所以附加阻力g为零。

现根据经验，假设待辨识参数初始值为：

根据定理1来确定学习增益的值，通过计算，得到一个合适的增益矩阵：

将θ0(t)的初始估计值和增益矩阵A代入迭代学习辨识器，执行迭代学习辨识任务，辨识结果如图5所示。

通过图5可以看出，经过16次迭代后，各参数的辨识值基本稳定，分别是：

从以上辨识结果可以得出，基本阻力参数a，b，c只与列车自身的型号有关，同一列车在任何线路上行驶时这些参数都不会发生变化，即基本阻力不会发生变化。但是，附加阻力g不是由列车自身性能决定的。当列车在不同的线路上运行时，由于线路的坡度各不相同，所以附加阻力g会不断发生变化。因此，当列车运行在另一条线路上时，需要重新辨识该参数。

综上所述，利用迭代法进行参数辨识既避开了列车控制系统难以建立精确的数学模型的难题，又利用了列车运行过程中包含的大量重复信息，能够解决由于控制经验不足或参数不全而导致控制效果不佳的问题，同时还能在列车运行过程中实时调整参数，极大地提高了跟踪控制效果。

5.2 列车运行曲线的跟踪仿真

列车在运行过程中会受到多种因素的影响，在对列车运行曲线进行跟踪仿真时，选取图4中剩余的22.6 km进行实验。此时，假设列车速度为112 km/h，位移为11.4 km，采用上节中所辨识出的未知参数计算基本阻力w(vk(t))，并结合式（7）给出的学习律，学习增益γ=0.6。

图5 各参数辨识结果

图6 期望的运行曲线

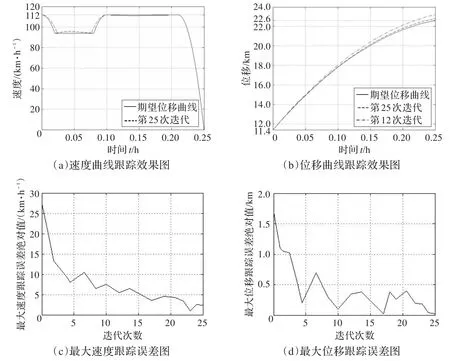
图7 实际的运行曲线及跟踪误差

列车在这一阶段的运行过程中要经历3个操作阶段：爬坡阶段，匀速运行阶段和制动停车阶段。根据列车的运行目标曲线，估计初始的控制输入如式（12）所示。

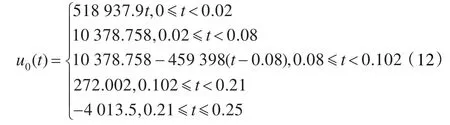
如图6（a）为列车运行时单位质量所受的附加阻力变化图，图6（b）和图6（c）为列车运行时的期望速度目标曲线图和期望位移目标曲线图。

进行迭代学习，当执行25次控制任务后，得到如图7所示的仿真结果。其中，图7（a）和图7（b）分别为速度曲线跟踪效果图和位移曲线跟踪效果图，显示了列车期望的运行曲线与实际运行曲线之间的关系。可以看出，随着迭代次数的增加，列车实际运行的速度曲线和位移曲线逐渐接近并最终与期望曲线重合，完成预定的行驶计划。图7（c）和图7（d）所示分别为最大速度跟踪误差图和最大位移跟踪误差图。从图中可以看出，列车的速度误差与位置误差随着迭代次数的增加而快速减小并保持在零附近。到第25次迭代时，最大速度跟踪误差和最大位移跟踪误差几乎收敛至零，表明控制任务已基本完成。有效地验证了本文提出的跟踪控制算法能够在确保列车安全运行的情况下使列车严格跟踪目标曲线行驶，且学习收敛速度快，控制效果明显，能够保证列车高精度、高平稳性的运行，极大地提高了乘客的舒适度。

6 结论

本文针对列车运行具有重复性的特点，将迭代学习控制引入ATO系统，研究了列车动力学模型中未知参数的辨识和列车速度控制算法。利用迭代法对参数进行辨识，能够克服由于控制经验不足和系统参数不全而无法准确建立列车动力学模型问题。同时，在列车运行过程中可以在线调整参数，提高系统的控制精度。利用迭代法对列车速度进行跟踪控制，实时连续地调整系统当前的输入量，使列车严格跟踪期望曲线行驶，避免列车频繁的加减速切换，缩短系统的学习时间，及时高效地实现对列车速度的控制，提高列车运行平稳性和旅行舒适度，具有良好的应用前景。

[1]刘贺文，赵海东，贾利民.列车运行自动控制（ATO）算法的研究[J].中国铁道科学，2000，21（4）：38-43.

[2]唐涛，黄良骥.列车自动驾驶系统控制算法综述[J].铁道学报，2003，25（2）：98-102.

[3]陈荣武，刘莉，诸昌钤.基于CBTC的列车自动驾驶算法[J].计算机应用，2007，27（11）：2649-2651.

[4]谢胜利，田森平，谢振东.迭代学习控制的理论与应用[M].北京：科学出版社，2005：54-59.

[5]窦鹏飞，王化琛.列车自动运行迭代学习控制算法的研究[J].计算机应用，2011，20（9）：5-9.

[6]王轶.基于迭代学习控制的几类列车自动控制问题研究[D].北京：北京交通大学，2010：19-24.

[7]Wang Yi，Hou Zhongsheng，Li Xingyi.A novel automatic train operation algorithm based on iterative learning control theory[C]//IEEE International Conference on Service Operations and Logistics，and Informatics，Beijing，2008：1766-1770.

[8]丁勇.列车运行计算与设计[M].北京：北京交通大学出版社，2011：38-52.

[9]中华人民共和国铁道部.列车牵引计算规程[Z].北京：中国铁道出版社，1999.

[10]裴九芳，王海，许德章.基于迭代学习控制的移动机器人轨迹跟踪控制[J].计算机工程与应用，2012，48（9）：222-225.

[11]Lee K S，Lee J S.Iterative learning control-based batch process control technique for integrated control of end product properties and transient profiles of process variables[J].Journal of Process Control，2003，13（7）：607-621.

[12]许建新，侯忠生.学习控制的现状与展望[J].自动化学报，2005，32（6）：943-955.

[13]李仁俊，韩正之.迭代学习控制综述[J].控制与决策，2005，20（9）：961-966.

[14]Park K H.An average operator-based PD-type iterative learning control for variable initial state error[J].IEEE Transactions on Automatic Control，2005，50（6）：865-869.

[15]Maday A.PID type iterative learning control with optimal gains[J].International Journal of Control，Automation，and Systems，2008，6（2）：194-203.

[16]侯忠生，金尚泰，赵明.宏观交通流模型参数的迭代学习辨识方法[J].自动化学报，2008，34（1）：64-71.