非高斯噪声背景下的诱发电位信号去噪方法

林政剑，熊美英，查代奉

LIN Zhengjian,XIONG Meiying,ZHA Daifeng

九江学院 电子工程学院，江西 九江 332005

College of Electronic Engineering,Jiujiang University,Jiujiang,Jiangxi 332005,China

1 引言

诱发电位（Evoked Potential，EP）是中枢神经系统所产生的生物电信号，诱发电位信号检测与分析技术是临床医学诊断神经系统损伤及病变的重要手段。近年来一些研究表明EP信号中伴随的EEG信号具有一定的脉冲特性。文献[1]的分析和实验表明，在诸如加速度撞击或缺氧等特殊实验条件下EP信号中的背景EEG噪声，信噪比常低于0 dB，可以用稳定分布模型来描述EEG噪声，比用常规的高斯模型具有更好的适应性。α稳定分布[2-3]的统计特性由其特征函数的四个参数来决定。概率密度函数没有统一的封闭表达式，但它的特征函数存在统一的形式。

其中，ω(t，α)=tan(απ/2)(α ≠ 1)，ω(t，α)=2lg|t|/π (α =1) 。α是特征指数(0＜α≤2)，控制着随机过程的脉冲程度，α愈小脉冲性愈强，当α=2时，稳定分布过程变为高斯分布过程；β是对称系数(-1≤β≤1)，β=0时表示对称α 稳定分布（symmetric α-stable），γ是分散系数 (γ≥0)，类似于高斯分布的方差；μ为位置参数，对应于均值或中值。其中，最重要的参数为特征指数α∈(0，2]。

由于小波分析适合对信号进行局部分析，能同时在时频域内对信号进行分析，近年来人们对小波去噪进行了广泛的研究。在小波变换中，能将信号与噪声在不同尺度上进行较好的分离。通过小波变换把信号能量集中到某些频带的少数系数上，通过将其他频带上的小波系数给予小的权重，即可达到有效抑制噪声的目的。

Mallat分析了白噪声在小波域中的特性，通过保存小波变换中的局部极大值来有效地抑制噪声[4]。Donoho在高斯模型的假设下，提出了一种简单易行的阈值去噪方法[5]。在实际的工程应用中，大多数信号可能包含尖峰和突变，而且噪声白信号也并不是平稳的噪声，对于脉冲噪声，Donoho的阈值去噪方法处理效果并不理想。针对特殊实验条件下EP信号中的具有显著脉冲特性的背景EEG噪声并且信噪比往往比较低的情况下的噪声抑制问题，本文采用先对含噪EP信号进行中值滤波预处理，有效抑制EEG噪声中的尖峰值，再利用小波阈值方法进行消噪，最终得到有用的EP信号。

2 中值滤波-小波去噪

由于传统的小波阈值方法不能有效抑制异常脉冲噪声[6]，本文将中值滤波和小波阈值方法结合，提出中值滤波-小波去噪算法，对脉冲噪声背景的诱发电位信号进行处理。

中值滤波[7-8]是一种去除噪声的非线性处理方法，基本原理是把n个数字信号x1x2…xn按值大小排列x(1)≤x(2)≤x(3)…≤ x(n)，中值定义为：

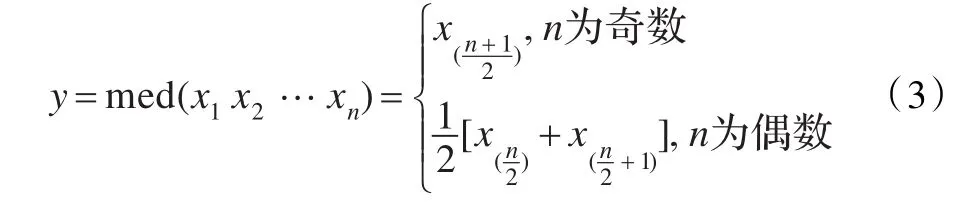
中值滤波器是一个有一定长度的滑动窗口，窗口正中的值用窗口内各值的中值代替，窗口的宽度影响噪声的平滑效果，窗口的宽度越宽，平滑效果越好，但可能导致过平滑现象，丢失信号的信息。窗口的宽度可以适当取小些，中值滤波主要去除峰值较大的脉冲噪声，剩余噪声近似高斯白噪声，可以用小波阈值方法[9-10]来处理。

Donoho的小波软阈值信号的形式为：

Cj，k为尺度水平 j下第 k 点的小波系数，为小波阈值处理后的小波系数，Tj为小波阈值，选择最优预测变量阈值。

3 仿真实验

取诱发电位（EP）信号（加速度撞击或缺氧窒息实验所获得的原始EP信号可以看作是准周期信号，周期为128点，采样频率为1000 Hz）与脉冲状EEG信号（由计算机模拟产生，特征指数α=1.6）混合[11]，如图1所示，其中s(n)代表纯净EP信号，x(n)代表含噪EP信号，信噪比设为10 dB，采用db4小波函数，分解层数为5，中值滤波滑动窗口大小分别设为2，5，10，分别采用Donoho小波阈值和本文方法进行仿真对比实验，去噪效果如图2～图4所示，其中s1(n)代表小波阈值消噪曲线，s2(n)代表本文方法消噪。

从图2～图4可以看出，传统的小波阈值去噪方法消噪后，仍然保留了脉冲噪声，失去了原始信号的特性，本文提出的方法能有效消除脉冲噪声，并很好地恢复原始EP信号。中值滤波器滑动窗口大小为2时，不能有效地去除脉冲噪声的影响，滑动窗口大小为10时，窗口过宽，产生过平滑现象，丢失信号的信息，滑动窗口大小为5时，比较好地兼顾去噪和保留原始信号的信息。

图1 纯净EP信号和含噪EP信号

图2 滑动窗口大小为2

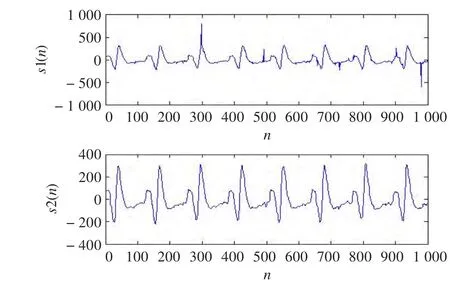
图3 滑动窗口大小为5

图4 滑动窗口大小为10

图5 传统小波阈值去噪和本文方法去噪均方误差曲线

图6 传统小波阈值去噪和本文方法去噪信噪比提高曲线

4 性能分析

为了进一步比较两种方法的去噪效果，在不同的信噪比情况下，分别仿真计算均方误差，如图5所示。

其中虚线代表传统小波阈值去噪均方误差曲线，实线代表本文方法去噪均方误差曲线，由图5可以看出，两种方法均方误差均随着信号的信噪比的提高而减小。但在信噪比小于10 dB情况下，本文介绍的方法明显优于传统小波阈值。

另一方面可以用信噪比提高值来衡量不同消噪方法的消噪效果。信噪比提高值[12]定义为：

SNR1，SNR2分别代表消噪前后的信噪比，单位为dB，信噪比定义为：

S(n)，N(n)和μ分别表示信号序列，噪声序列和噪声均值。

分别在不同的输入信噪比情况下，仿真传统方法和本文方法得出信噪比提高曲线如图6所示，其中实线代表本文方法，虚线代表传统小波阈值去噪。

由图6可知，随着输入信噪比的提高，本文方法信噪比提高值减小，但在信噪比小于10 dB情况下，本文方法信噪比提高值明显大于传统小波阈值去噪信噪比提高值。

5 结论

α稳定分布可以较好地描述在诸如加速度撞击或缺氧等特殊实验条件下具有显著脉冲特性的EEG信号，在信噪比较低的情况下，传统的小波去噪方法不能有效地去除EP信号中具有尖峰脉冲特性的背景噪声的影响。中值滤波预处理的消噪方法在低输入信噪比情况下，能有效地抑制EP信号中的尖峰脉冲，可以极大地改变传统的小波去噪方法的性能，表现出良好的韧性。

[1]Kong X，Qiu T A.Adaptive estimation of latency change in evoked potential sby direct least mean p-norm timedelay estimation[J].IEEE Transactions on Biomedical Engineering，1999，46（8）：994-1003.

[2]Nikia C L，Shao M.Signal processing with alpha-stable distributions and applications[M].New York：John Wiley&Sons Inc，1995.

[3]Shao M，Nikias C L.Signal processing with fractional lower order moments：stable processes and their applications[J].Proceedings of IEEE，1993，81（7）：986-1010.

[4]Mallat S，Hwang W L.Singularity detection and processing with wavelets[J].IEEE Transactions on Information Theory，1992，38（2）：617-643.

[5]Donoho D L.De-noising by soft-thresholding[J].IEEE Transactions on Information Theory，1995，41（3）：613-627.

[6]李翰芳.一种新的非高斯分布噪声下的小波去噪方法[J].湖北工业大学学报，2011，26（2）：136-139.

[7]Fitch J P，Coyle E J，Galagher N C，et al.Median filtering by threshod decomposition[J].IEEE Transactions on Acoust Speech，Signal Proc，1984，32（6）：1183-1188.

[8]刘丽梅，孙玉荣，李丽.中值滤波技术发展研究[J].云南师范大学学报，2004，24（1）：23-27.

[9]李海东，李青.基于阈值法的小波去噪算法研究[J].计算机技术与发展，2009，19（7）：56-58.

[10]许文博，武晓春，邢建平.一种新的小波阈值去噪方法[J].兰州交通大学学报，2012，31（3）：120-124.

[11]查代奉，高玉，熊美英，等.非高斯噪声下基于MD准则与Givens旋转的EP信号提取方法[J].生物医学工程学杂志，2010，27（3）：495-499.

[12]简涛，苏峰，何友，等.针对拖尾噪声的中值滤波-小波去噪算法分析[J].信号处理，2007，23（1）：79-82.