基于粒子群三次样条优化的图像边缘描述算法

公亚利, 林意

江南大学数字媒体学院,江苏 无锡 214122

Gong YaLi , Lin Yi

School of Digital Media, Jiangnan University, Wuxi 214122，China

1.引 言

在图像研究和应用中，人们一般只对图像中的某些部分感兴趣，这些部分对应图像中特定的、具有独特性质的区域，一般称之为目标。为了辨识和分析目标，需要将这些区域分离出来，在此基础上才有能对目标区域进一步应用[1]。而要分离这些区域，首先要得到图像区域的边缘。图像区域边缘不仅能够勾画出目标轮廓,使观察者一目了然，而且蕴含丰富的内在信息。因此，图像目标边缘检测技术被广泛研究并在不同的领域应用。

一般的边缘检测算法中，图像边缘以离散点集的形式给出，受噪声的影响较大，检测结果不可靠，无法准确判定边缘是否存在，也无法给出其准确位置，不利于区域的形状描述及应用。相比较而言，边缘表达式要简单得多。该方法先通过指定少量的型值点来定义一个大概的曲线轮廓，然后利用样条曲线来拟合选定的型值点，就可以得到大致的图像边缘。

边缘表达式即可以克服图像边缘点集数据量大的缺点，又能很好反应边缘的一些形态和拓扑结构，同时还克服了链码、多边形的粗糙性[1]。

三次参数样条曲线方程可以作为边缘表达式来描述图像边缘。但从实验中发现，手工选点拟合生成的三次参数样条曲线与图像边缘点集的一致性较差。虽然有较高的逼近度，但不能很好地贴合边缘点集。主要表现在曲线与边缘点集的交叉很多，导致曲线对应的边缘点集失去了其实际应用价值。针对这一问题，通过深入研究粒子群算法[2-3]，发现该算法具有个体数目少、计算简单、收敛速度快等特点，可以用于描述图像边缘的三次参数样条曲线的优化。因此，本文利用粒子群算法来优化三次参数样条曲线，通过优化三次参数样条曲线的型值点，使优化之后的样条曲线形态和边缘轮廓一致，对边缘有较好的贴合。其核心思想是通过利用粒子群算法搜索样条曲线的新型值点[4]，然后用边缘检测算子[5]来评估经过调整的型值点，调整粒子群算法搜索的方向。不断地进行迭代搜索，最终得到一组型值点，使用该组型值点拟合出的样条曲线可以较好的贴合图像边缘。实验表明该算法能够快速拟合曲线，且拟合得到的曲线平滑贴合图像边缘。

2.构造样条曲线

本节介绍本文构造样条曲线函数的方法。

首先，在图像区域的边缘上取一组外型曲线的型值点列向量 Vj=(xj, yj)(j=0,1,…,n)，然后通过该组型值点构造三次参数样条参数插值曲线[6-9]，所求三次参数样条曲线 r(t)=(x(t),y(t))，向量 r(t)符合 ：

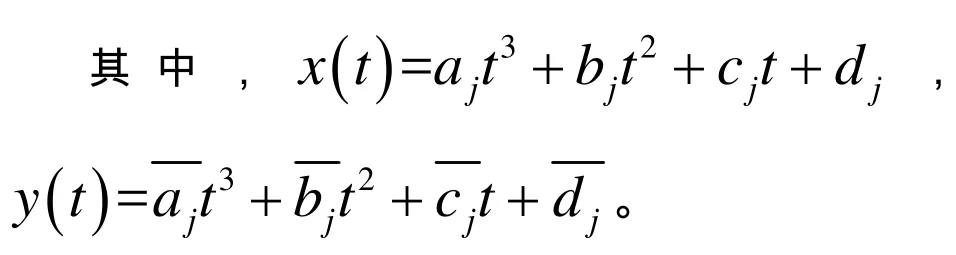
参数t取累加弦长，即：t0=0,t1=|V1-V0|,…,tn=tn-1+|Vn-Vn-1|，在分Δ:t0≤t1≤t2≤t3≤t4…≤tn-2≤tn-1≤tn上作三次样条参数曲线。由(1)式知，x(t)和 y(t)的形式相同，故仅给出x(t)的构造过程。

设型值点Vj的切向量mj=(mxj,myj)T已知。将xj-1,xj,mxj-1,mxj代入x(t)得到：

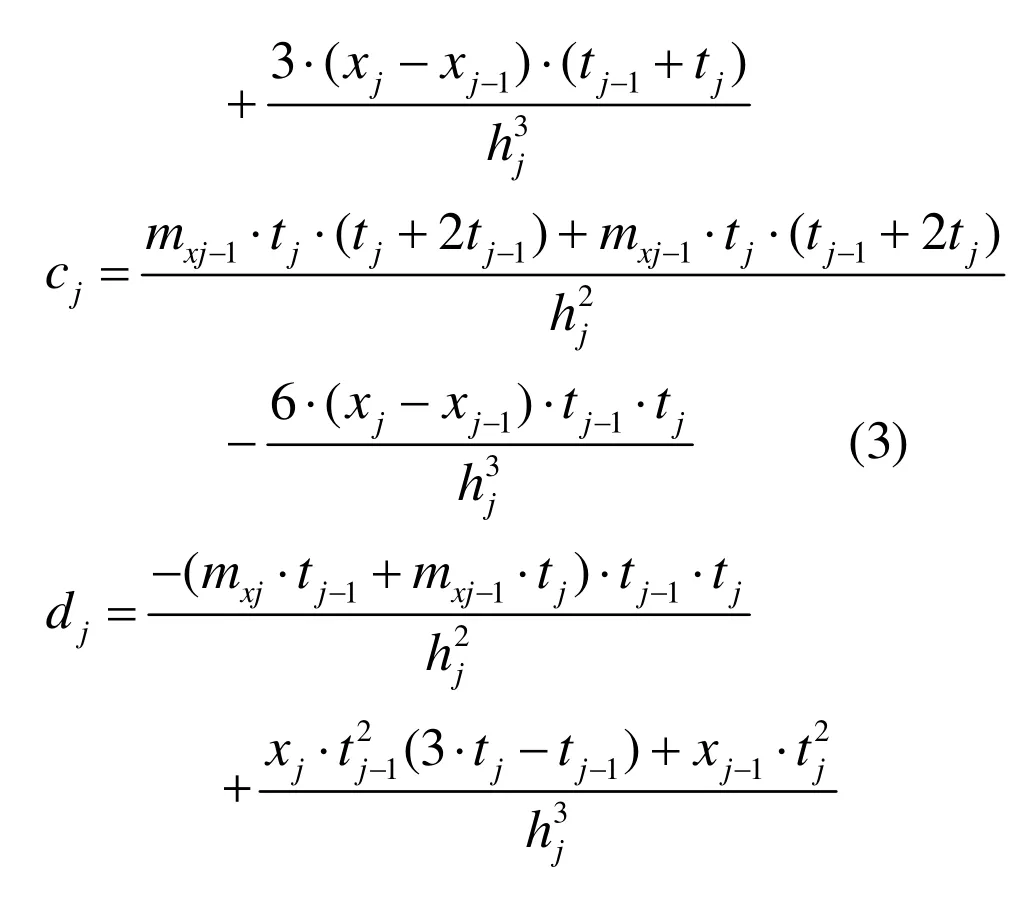
又由于三次参数样条曲线在整个区间上C2连续，即xj-1(t), xj(t)在t=tj处二阶导数连续，即：

由式(4)可推得：

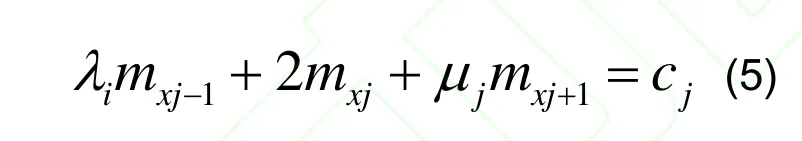
其中 ：

该方程组是关于未知数m0,m1,…,mn的n-1个方程，需添加两个边界条件：

其中，边界条件为手工设定。联立式(5)、(6)可以求出mxj(j=1,…,n-1)，将其代入(3)求出参数曲线x(t)。同理，可以求出y(t)。

3.粒子群算法

本文把图像边缘样条曲线优化看作是在三次样条空间中搜索最佳型值点的过程。

在使用粒子群算法[10-12]对三次样条曲线进行优化之前，首先需要建立粒子。

设样条曲线中有n个型值点，则整条曲线中共有(n-1)条样条曲线段。由式(5)可知每条曲线段均由其两端的两个型值点决定。首尾型值点包含有边界切向量的信息，因此在构造过程中除去首尾型值点。仿照文献[11]建立了于三次参数样条曲线优化的2(n-2)维粒子L，用向量表示为：

在搜索过程中，每个粒子都有一个2(n-2)维的速度向量 v=＜v1, v2, v3, v4, v5,…,v2n-1,v2n-2＞，其中，vi(i=1,2,3,…,2 n-1,2 n -2)为每个维度上的速度分量，在粒子初始化时被随机赋值为介于MAX_SPEED和MIN_SPEED之间的一个值。

MAX_SPEED和MIN_SPEED为算法输入变量，其限制了粒子群在一次搜索时运动速度的范围。

在迭代过程中，粒子根据两个极值来更新自己。第一个为粒子本身找到的最优解，称为个体极值，即 Pbesti；第二个极值为整个种群目前找到的最优解，称为全局极值，即Gbesti。粒子根据这两个极值来更新自己。

三次样条参数曲线中，对一个型值点的调整对它相邻两个型值点的影响最大，对其余型值点的影响迅速减小。针对这个特点，对粒子群算法的速度公式进行了修改，引入了影响因子，用来描述某个型值点受到其左右两个型值点变化的影响。经过修改的速度公式如下：

该式用来计算某个速度的各个速度分量，其中vi表示速度的第i个分量；Li表示粒子的第i个分量； ω表示惯性权重；c1，c2为学习因子； r1和r2为两个均匀分布在(0,1)之间的随机数； n1，n2为邻型值点影响因子，n1表示速度分量受到左型值点影响的影响因子，n2表示速度分量受到右型值点影响的影响因子； vl,vr分别表示左型值点的速度分量和右型值点的速度分量。

4 适应度函数

本文将三次样条曲线用于图像边缘提取，因此评价拟合之后的样条曲线的好坏最重要的依据就是拟合之后的样条曲线是否贴近被提取图形的边缘。所以本文使用典型的边缘检测算子来对生成的曲线进行评价。

4.1 图像边缘检测算法

边缘检测的基本算法有很多,如梯度算子、方向算子、拉普拉斯算子和坎尼(Canny)算子等等。常用的边缘检测方法则有Roberts算子、Sobel算子和Prewitt算子、高斯偏导滤波器(LOG)以及Canny边缘检测器等。常用的边缘检测算子[13-14]中比较优秀的是Canny算子。但由于该算子在使用之前需要将图形高斯化，使用起来比较复杂，因此本文使用Sobel算子来对曲线进行评价。

Sobel算子是一阶导数的边缘检测算子。在算法实现过程中，通过3×3模板作为核与图像中的每个像素点做卷积和运算，然后选取合适的阈值以提取边缘。采用3×3邻域可以避免在像素之间内插点上计算梯度。即：

(a)图像邻域模板

Sobel算子也是一种梯度幅值，即：

其中偏导数Sx 和Sy可用卷积模板来实现，即：

Sobel算子算法的优点是计算简单，速度快。因此，为了检测特定方向上的边缘，减少噪声点的影响，本文采用不同方向的Sobel算子模板如下所示：

(b)Sobel算子模板

图像中的每个像素点均用(b)中的四个核做卷积，将四个卷积核的最大值作为该点的输出值。

4.2 适应度函数的选取

适应度函数用来对样条曲线进行评价。本文使用图像边缘检测中典型的Sobel算子为基础编写适应度函数。评价好坏的依据就是拟合之后的样条曲线是否贴合被提取的图像边缘。评价过程分为三个层次:

(1)粒子的比较。首先分别抽取当前粒子中的参数和对比粒子中的参数来拟合两条曲线，然后通过比较这两条曲线的优劣来判断粒子的优劣。

(2)拟合曲线的比较。通过比较曲线上各个拟合点的优劣来得出的，拥有更多比较中占优的拟合点的曲线更加优秀。

(3)拟合点的比较。通过比较拟合点的图像边缘检测算子卷积的大小来判断，卷积大的，对应的拟合点就更优秀。

拟合点的比较决定曲线比较的结果，曲线比较的结果又会决定粒子比较的结果。最终得出哪个粒子更优秀，更加优秀的粒子意味着该粒子对应的拟合曲线更贴近图像边缘。更加优秀的粒子会被用来更新 Pbesti和 Gbesti。

5.算例

本文为了验证上文中给出的优化算法，分别给出了固定粒子规模、变化迭代次数和固定迭代次数、变化粒子规模的两个算例。

5.1 粒子规模固定，迭代次数变化

首先，选择4个型值点，拟合优化前的三次参数样条曲线(a)(黑色点为型值点，黑色实曲线为优化前的三次参数样条曲线)。然后将粒子规模固定为10，迭代次数分别为10、15、20次，拟合的三次参数样条曲线分别是(b)、(c)、(d)(黑色虚线为优化后的三次参数曲线），其不同参数的迭代次数效果对比图如图1所示：

图1 不同参数的效果图Fig.1 The effect of different parameters

图1中三次参数样条曲线在优化前后的曲率对比如图2所示：

图2 曲率对比图Fig.2 Curvature effect drawing

如图1所示，(a)优化前拟合的三次参数样条曲线，其首尾型值点附近的曲线段偏向于图像区域边缘外侧，中间的曲线段偏向于图像区域边缘内侧。依据优化后的曲线段要更加贴合图像边缘的要求，曲线的变化趋势应该是两侧曲线曲率变小，中间部分的曲率变大。如图2所示，优化前后曲线的曲率变化趋势大体上符合上述推测。优化后的曲线更平滑、更贴近图像区域边缘。因此，在粒子规模固定的情况下，随着迭代次数的增加，粒子群搜索结果拟合的曲线越来越贴合图像边界。

5.2 迭代次数固定，粒子规模变化

首先，选择了4个型值点，拟合优化前的曲线(e)(黑色点为型值点，黑色实曲线为优化前的三次参数样条曲线)。然后将迭代次数固定为10，粒子规模分别为10、15、20个，拟合的三次参数样条曲线分别是(f)、(g)、(h)(黑色虚线为优化后的三次参数样条曲线)，其不同参数的迭代效果对比如图3所示:

图3 不同参数的效果图Fig.3 The effect of different parameters

图3中的三次参数样条曲线在优化前后的曲率对比如图4所示：

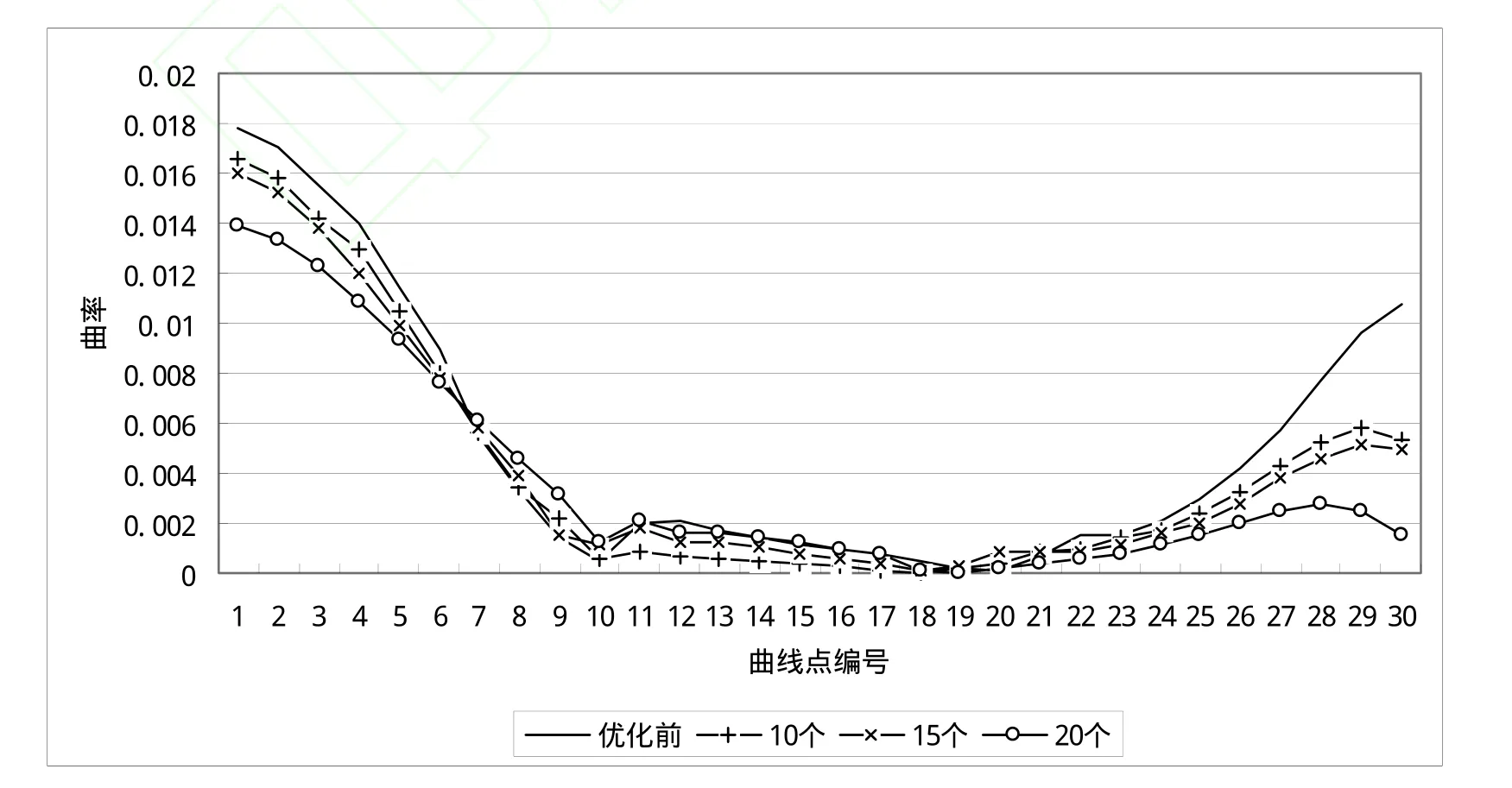
图4 曲率对比图Fig.4 Curvature contrast diagram

如图3所示，(e)优化前拟合的三次参数样条曲线，其首尾型值点附近的曲线段偏向于图像区域边缘外侧，中间的曲线段偏向于图像区域边缘内侧。依据优化后的曲线段要更加贴合图像边缘的要求，曲线的变化趋势应该是两侧曲线曲率变小，中间部分的曲率变大。如图4所示，优化前后三次参数曲线的曲率变化趋势大体上符合上述推测。优化后的曲线更平滑、更贴近图像区域边缘。因此，在迭代次数固定的情况下，随着粒子群规模的增加，粒子群搜索结果拟合的曲线越来越贴合图像边界。

6.结束语

本文利用粒子群算法结合边缘检测算子优化手工选点生成的三次参数样条曲线，在手工确定边界切向量的情况下，利用粒子群算法修改插值曲线的型值点，以边缘检测算子为基础形成评价函数，并用其评估优化之后的曲线。实验表明，优化后的样条曲线既能较好地逼近区域边缘又能够达到平滑的效果，并对图像边缘有很好地贴合，能够用于对图像边缘的描述。由于粒子群规模和迭代的次数对图像边缘的贴合有直接的影响，当粒子群规模和迭代次数很大时，优化速度较慢。另外，型值点的个数对图像边缘曲线的拟合也有影响。这些都有待于进一步的研究。

Reference)

[1]林意，吴锡生.一种图像区域边缘表达方法[J].重庆大学学报，2006，29(7)：77-80.

[2]杨 维, 李歧强.粒子群优化算法综述[J].中国工程科学，2004，6(5)：87-94

[3]李爱国，覃 征，鲍复民等.粒子群优化算法[J]，计算机工程与应用，2002，(21):1-3,17

[4]Huaiping Yang,Wenping Wang,Jiaguang Sun.Control point adjustment for B-spline curve approximation[J].Computer-Aided Design,2004,(36),,639-652

[5]沈丽容.图像边缘检测算法比较研究[J].福建电脑，2011，(5)：5-9

[6]王仁宏，李崇君，朱春钢.计算几何教程[M].北京：科学出版社，2008：48-60.

[7]方逵，张启松，李建平.计算机辅助几何设计[M].河北：河北教育出版社，1994：29-49.

[8]孙家广，杨长贵.计算机图形学(新版)[M].北京：清华大学出版社，1997：284-294.

[9]叶康伦.样条应用与曲线光顺[J].广船科技，2003，(1)：11-25

[10]Russell C.Eberhart, Yuhui Shi.Particle Swarm Optimization:Developments,Applications and Resource[J].Evolutionary omputation,2001,(1),81-86

[11]权国通，谭 超，侯海潮等.基于粒子群三次样条优化的采煤机截割路径规划[J].煤炭科学技术，2011，39(3)：77-79

[12]吴宪祥，郭宝龙，王 娟.基于粒子群三次样条优化的移动机器人路径规划算法[J].机器人，2009，31(6)：556-560

[13]谭 艳，王宇俊，李飞龙等.几种典型的图象边缘检测算法的分析比较[J].电脑知识与技术，2012,8(7)：1604-1608

[14]赵来刚，陈道炯.一种基于 Sobel算子的新型边缘提取算法[J].机械与电子，2011,(2):59-61