鱼眼畸变棋盘格图像校正
黄岩岩 ,李 庆 ,张斌珍
HUANG Yanyan1,2,LI Qing2,ZHANG Binzhen1
1.中北大学 仪器与电子学院,太原 030051
2.中国科学院 微电子所昆山分所,江苏 昆山 215300
1.Instruments and Electronics Institute,North University of China,Taiyuan 030051,China
2.Kunshan Department,Institute of Microelectronics of Chinese Academy of Sciences,Kunshan,Jiangsu 215300,China
随着鱼眼镜头的广泛应用,科学家们对鱼眼畸变的校正作了大量的研究。目前,校正领域大致分为三类:平面校正,柱面校正和球面校正。平面校正中具有代表性的是透视投影和立体投影校正[1],共同的缺点是局限于镜头视野的大小,当视野较大时出现向外围拉伸的现象,视野接近180°时无限拉伸。柱面校正具有代表性的是Mercator投影校正[2-3],该校正方法的水平视野可以达到很宽,但垂直视野达到180°时和平面校正结果一样,出现无限拉伸现象。球面校正具有代表性的是经纬展开校正[4-5],展开后的图像在两极出现弯曲,无法满足视觉质量。鱼眼镜头的成像过程可以近似为一个球模型的投影,而球面是一个不可展的表面[6],以上的校正方法都是从球体视觉到平面视觉的全局映射校正,所以都不可避免地包含了一定程度的失真[7],因此,鱼眼图像的校正只能最大限度地近似将球面图像转换为平面图像。Carroll等人[8]的校正方法就是根据图像中弯曲的直线信息在目标图像中最大化近似为直线,得到空间变化的映射关系的校正结果图像。基于Carroll等关于鱼眼图像校正的工作,针对包含棋盘格的畸变图像,提出一种简单可行、自动快速的鱼眼图像校正方法。
1 Carroll等基于内容的校正原理
1.1 用户接口
人的视觉往往侧重于场景中的突出特征,而不是整个场景。利用这一点可以通过非线性优化的方法达到尽量保留突出特征的正常视觉的投影。Carroll等人基于内容的映射方法是一种根据用户指定约束特征优化得到空间变化映射的投影方法。用户需要手动输入直线的两个端点,指定图像中的直线特征。
1.2 建立数学方程
鱼眼畸变图像投影到球面坐标,用球坐标经线λ和纬线ϕ将球面参数化,校正后的平面图用坐标u,v参数化。向量形式为 λ=(λ,ϕ),u=(u,v)。可以用两个函数u(λ,ϕ),v(λ,ϕ)或一个向量 u(λ)表示映射。
向量h和k描述映射的局部特性:

如果h是k的90°旋转,那么映射就是保形的:

映射函数u(λ)是局部变化的约束,所以得不到一个闭合形式解。相反,将映射抽样离散为均匀的网格(λ,ϕ),对于(i,j),定义V 为所有顶点(i,j)的集合。这些顶点在球表面形成四边形网格。通过优化计算得到λi,j对应的 ui,j。
1.3 保型性
通过离散柯西黎曼方程给出网格的保型性约束:

解微分方程时等式两边同时乘以一个常数对结果没有影响。然而,用最小二乘法解离散方程时改变约束的权值将影响结果。球视图上的四边形大小不一,同样的权值约束保型性就会偏向四边形密度高的区域。因此根据四边形面积给定权值,纬度ϕ处的权值正比于cos(ϕ)。乘以约束cos(ϕ)来定义保型性的能源函数为:

其中wi,j为空间变化权值。
1.4 直线特征
定义Vl是直线交叉四边形顶点(i,j)的集合。一条直线的两个端点定义为ustart和uend。其余部分丢弃上标l假定u对应特定线的顶点。
点u到连接两个端点ustart和uend的直线的距离为(u-ustart)Tn(ustart,uend),其中

为线的法向量,R90是矩阵的90°旋转。约束直线l的能量函数为:
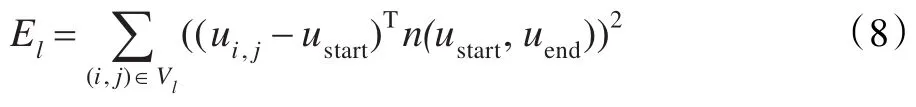
这个能源函数是非线性的,用非线性优化技术高斯-牛顿或LM来解。通过另外两种可以线性解决的方式简化方程。可以用(u-ustart)和它投影到直线上的切向量来表示点u到直线的距离,这样能源函数可以等价为:
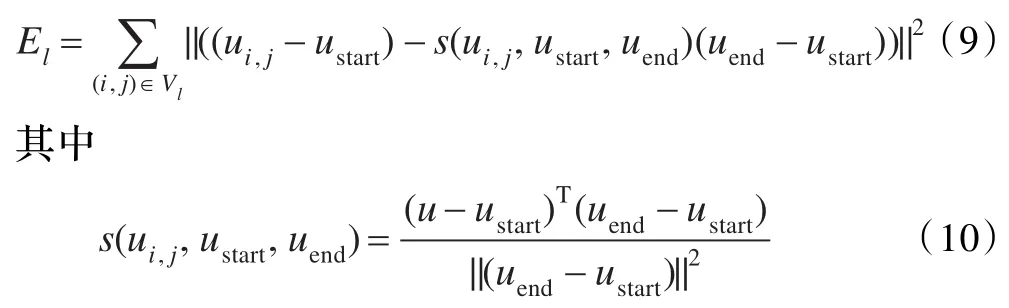
是(u-ustart)投影到 uend-ustart的归一化距离,这样s(ustart,ustart,uend)=0 ,s(uend,ustart,uend)=1 。现在有两种方式简化直线能源函数:固定方程(8)的法向量得到,固定方程(9)的归一化投影得到。

简单来说,这些线性能源项允许用两种不同的方式减少总的直线能源:Elo使得点在线的方向固定的情况下可以在线上自由滑动,Eld使得线的方向可以改变同时预防点在线上滑动。使用两种线性能源交替的迭代最小化方案。
1.5 平滑度
仅仅保型性和直线约束可能会导致投影的视觉假象。由于保型性不考虑尺度或方向,投影在图像空间上会剧烈变化,尤其是线段。加上平滑度约束,限制了尺度和方向变化的快慢。用差分北向量h来形成平滑约束。如果h变化很慢,那么方向和尺度变化也很慢。所以,用最小二乘法选择:

直观地,这个约束最小化了映射的弯曲度。有限差分近似为二阶导数来离散这组方程。权值为cosϕi,j,取∂h/∂λ为平滑度能源函数。
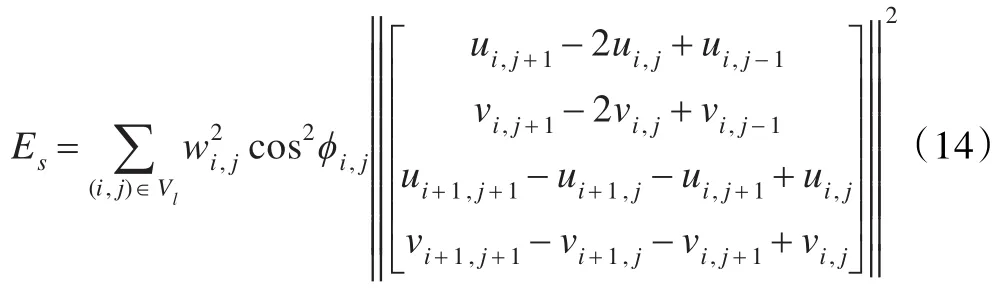
其中wi,j是空间变化权值。
1.6 总的能量函数和优化
每个顶点的空间变化的权值,也用全局权值对每一项设定它们的相对重要性。总的能源函数就是保型性,平滑度和直线能源的加权和:

有固定方向的直线,用固定方向函数代替一般的直线能源项。为解决最小化问题,交替使用固定方向线的能源函数优化和固定的归一化投影总能源函数。

使用PARDISO稀疏直接求解器求解这个系统方程。最后使用双线性纹理映射渲染网格得到校正的图像。
2 棋盘格图像校正方法
Carroll的方法需要用户指定输入直线特征,这种交互使得自动化程度低,使用过程不便捷。此外函数方程的优化过程需要8到10次两步迭代才能收敛,时间花费较大。针对特殊棋盘格图像的畸变校正,可以通过角点检测实现自动输入信息,并采用闭合形式求解方程减少时间花费,这样棋盘格图像就可以实现自动、快捷的畸变校正。
2.1 角点检测
角点检测的研究目前已经有很多成熟的算法[9-13],针对棋盘格的角点检测算法精度、准确度都较高,这里选择Martin Rufli等人[14]提出的基于提取封闭轮廓区域的棋盘格角点检测算法。首先对输入的图片进行自适应阈值二值化,然后在不同腐蚀次数下查找轮廓逼近四边形,并与邻近的找到的四边形相连,最后由相邻的四边形顶点确定最终的角点坐标,同时按其所在的行列顺序排列这些角点,记录行列号。
对上述角点检测算法,用不同腐蚀阈值[15]系数求得坐标的累计期望值可以提高坐标精度。计算如下:
(x,y)=((x1+x2+ … +x9)/9,(y1+y2+ … +y9)/9) (18)
其中,x1,x2,…,x9,y1,y2,…,y9是 9 次不同阈值下求得的坐标,(x,y)是最终的均值坐标,提高了角点的精度。
在获得角点的行列坐标号后,将每行、每列的角点分别存储,这些相同行列的角点位于同一条直线上,因此,可以作为直线特征的输入信息,无需人工给出直线再获得直线坐标信息。对输入图片的角点检测及行列标号示意图如图1所示。

图1 角点检测示意图
2.2 应用Carroll校正优化
Carroll等人提出的是一种基于网格的非线性优化技术,人工输入畸变图上直线的两个端点,再由球面投影约束计算直线的轨迹,然后利用球面坐标离散化得到直线上的像素点的信息。利用这些像素点坐标建立数学方程,求解过程采用迭代求解计算,花费时间很长。
对于棋盘格畸变图像,直接采用同行同列的角点坐标作为输入信息建立能源函数方程。省去了人工输入直线的端点,并计算直线轨迹算法的部分。将得到的非线性能源函数,使用一个对称正定线性系统设置为Ax=b≠0,然后对此线性方程进行最小化[6]。

这样就转化为求解 y的最小值问题。最小二乘法(又称最小平方法)是一种数学优化技术。它通过最小化误差的平方和寻找数据的最佳函数匹配,即使得:

为最小值。使用最小二乘公式标准线性求解器,可得到一个闭合形式解,该解即为空间变化的映射关系。最后根据这个映射关系投影利用双线性插值得到校正图像。校正结果见2.3节。
在一台32位操作系统,2.8 GHz的主频,2 GB内存的PC上,对于一幅大小为360×240,棋盘格角点个数为160个的图像,Carroll方法的优化步骤需要8到10次两步迭代才能收敛,一步迭代要花费大于1 s的时间,平均处理一幅图像要超过12 s的时间。通过对方程的线性优化求解唯一解,计算量下降,再加上自动角点检测算法所占的计算量和时间0.7 s,校正一幅图像大概需要2 s,花费的时间比原来大大减少。
2.3 校正结果比较
在实验室拍摄一幅带有棋盘格的鱼眼图像,横向视野180°,纵向视野156°,大小为320×240,棋盘格角点为160个。和其他几种类型的校正结果进行了比较。图2是原始畸变图,图3是平面透视投影校正,图4是柱面投影校正,图5是球面经纬展开校正。利用上文提到的方法得到的校正结果如图6所示。

图2 原图

图3 透视投影校正

图4 柱面投影

图5 经纬展开

图6 本文算法的校正
通过比较上述几幅校正结果图,可以看出,透视投影导致外围严重的拉伸,Mercator柱面投影校正垂直线很好,但不能校正横跨视野的水平线。球面经纬展开校正的结果在边缘处出现弯曲,使用本文的方法主要特征校正结果良好。
3 结束语
研究了Carroll等人的基于内容的畸变图像校正原理,针对其需要人工参与、半自动化、时间复杂度高的缺陷,结合畸变棋盘格图像的应用场景,提出了一种自动校正算法。首先利用自动角点检测算法将获得的角点信息作为输入信息,建立数学模型求解,然后对目标函数进行线性优化求解,大大提高了计算效率。改进后的算法完全实现自动化,简单高效。经实验表明,此方法的校正结果良好。
[1]Hughes C,Denny P,Jones E.Accuracy of fish-eye lens models[J].Applied Optics,2010,49(17):3338-3347.
[2]Liu Y C,Lin K Y,Chen Y S.Bird’s-eye view vision system for vehicle surrounding monitoring[C]//Proceedings Conference Robert Vision,2008:207-218.
[3]周辉,罗飞,李慧娟,等.基于柱面模型的鱼眼影像校正方法的研究[J].计算机应用,2008,28:2664-2666.
[4]Swaminathan R.Nonmetric calibration of wide-angle lenses and polycameras[J].Pattern Analysis and Machine Intelligence,2000,22(10):1172-1178.
[5]杨玲,成运.应用经纬映射的鱼眼图像校正设计[J].工程图学学报,2010(6):19-22.
[6]Jin Wei,Li Chenfeng,Hu Shimin.Fisheye vedio correction[J].IEEE Transactions on Visualization and Computer Graphics,2012,18(10):1771-1783.
[7]Kopf J,Lischinski D,Deussen O,et al.Locally adapted projections to reduce panorama distortions[J].Computer Graphics Forum,2009,28(4):1083-1089.
[8]Carroll R,Agrawala M,Agarwala A.Optimizing content preserving projections for wide-angle images[C]//SIGGRAPH 2009,2009.
[9]Malik J,Dahiya R,Sainarayanan G.Harris operator corner detection using sliding window method[J].International Journal of Computer Applications,2011,22(1).
[10]Chen Jie.The comparison and application of corner detection algorithms[J].Journal of Multimedia,2009,4:435-441.
[11]Zhao Wanjin,Gong Shengrong.Adaptive harris corner detection algorithm[J].Computer Engineering,2008,10:218-220.
[12]刘阳成,朱枫.一种新的棋盘格图像角点检测算法[J].中国图象图形学报,2006(5):656-660.
[13]房超,王小鹏,牛云鹏.基于改进Harris算法的角点检测[J].计算机与数字工程,2011,39(5):142-144.
[14]Rufli M,Scaramuzza D,Siegwart R.Automatic detection of checkerboards on blurred and distorted images[C]//Intelligent Robots and Systems,2008:3121-3126.
[15]冈萨雷斯.数字图像处理[M].阮秋琦,阮宇智,译.2版(中文版).北京:电子工业出版社,2007.

