基于Matlab机械臂力控系统仿真研究

覃海强,熊庆宇,2,石 欣,王 楷

QIN Haiqiang1,XIONG Qingyu1,2,SHI Xin1,WANG Kai1

1.重庆大学 自动化学院，重庆 400044

2.重庆大学 软件学院，重庆 400044

1.School of Automation，Chongqing University，Chongqing，400044，China

2.School of Software Engineering，Chongqing University，Chongqing，400044，China

1 引言

随着科技的进步，机械臂在生产自动化中占有越来越重要的地位。机械臂在执行装配、抛光、去毛刺等任务时，都会与环境相互接触，并且产生相互的作用力，太大的作用力会损坏机械臂及其加工工件, 因此必须对机械臂的受力进行有效控制。为了有效地实现复杂机械臂系统的力控制并降低风险节约成本，对机械臂力控制系统进行仿真验证是一种有效的途径。SimMechanics是Matlab 中的机构系统模块集，它可以对各种运动副连接的刚体进行建模与仿真，达到对机构系统进行分析与设计的目的。SimMechanics与其它仿真平台相比，最大的优点是无需建立机构运动的数学模型和编制程序，并且具有系统建模方便直观和仿真功能强大的特点，能大大减轻设计人员的工作，为机械系统的建模仿真提供一个强大而方便的平台。因此，本文采用 SimMechanics仿真平台，对二自由度机械臂力控系统进行仿真与研究，进而实现对工业机械臂在完成特定作业时与环境间接触力的控制。

力控就是对机器人末端执行器输出力或关节力矩的控制。最早将力控用于多关节机器人上的是Whitney，他将力传感器用在多关节机器人上，并用解运动速度的方法（RMRC）推导出力反馈控制的向量表达式[1]。P.Fraisse, F.Pierrot和P.Dauchez首先提出虚拟环境下的机械臂力控制, 此方法可以增强机械臂力控制方案的鲁棒性[2]；Gabriel Afonso和J.Norberto Pires针对工业机械臂在进行抛光作业的过程中提出一种行之有效的力控方法，使机械臂能够以期望的接触力在期望的位置上运动，最终完成机械臂的抛光作业[3]。

本文根据机械臂的抛光任务，以平面二自由度机械臂为研究对象，对其进行动力学分析，并在Matlab/SimMechanics中建立其机械模型与力控系统，在平面中模拟机械臂末端与环境间的接触面，实现对平面二自由度机械臂的力控，使机械臂在力控制下完成预期的运动轨迹。同时设计振荡抑制控制器，实现机械臂与刚性环境碰撞接触过程中冲击振荡阶段的振荡抑制。

2 机械臂动力学模型

不考虑摩擦力等外界干扰的作用，n自由度机械臂动力学方程为[4]：

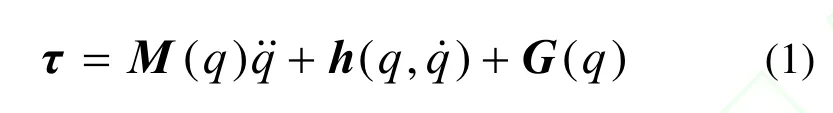
其中，M(q)为正定的惯性矩阵；h(q, q˙)为离心力和哥氏力矢量；G(q)为重力矢量；q为关节位置；τ为关节驱动力矩。

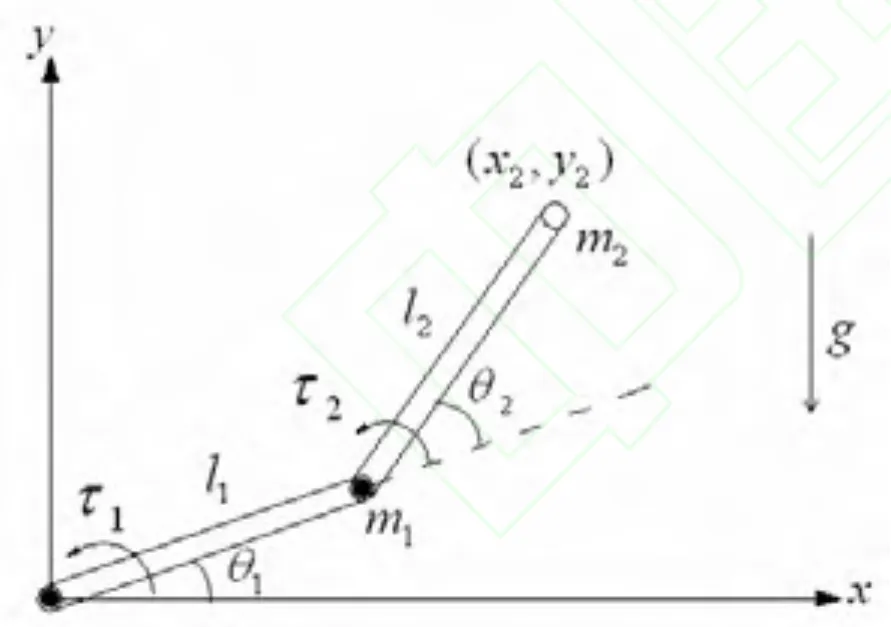
图1 平面二自由度机械臂

在平面中建立二自由度机械臂模型如图 1所示，假设机械臂为刚性，两个关节均为转动关节，且每个连杆的质量都集中在连杆的末端。两个连杆的质量分别为m1和m2；长度分别为l1和l2；关节角位置为；关节力矩为

平面二自由度机械臂动力学方程为：

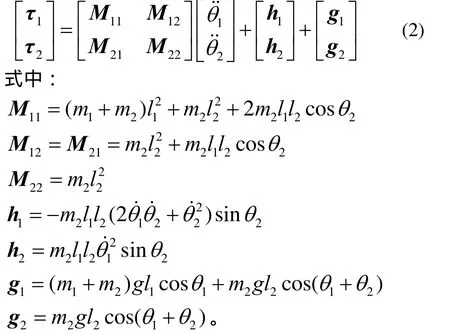
在笛卡尔坐标系中，当机械臂末端与外部环境相互接触时[5]，机械臂与外界将会产生相互的作用力Fe，为了保持机械臂的平衡状态，必须对各个关节施加一定的驱动力矩τ，且有，其中，J为机械臂的雅可比矩阵，JT为机械臂雅可比矩阵的转置，且有：

通过 JT可将作用在机械臂末端的笛卡尔力映射成为等效的关节力矩。与环境相接触时，机械臂的动力学方程为：

3 平面二自由度机械臂力控

3.1 机械臂的力控

根据机械臂动力学，设计机械臂的力控系统如图 2所示，其中，Fd为笛卡尔坐标系中机械臂末端所受的期望外力；Fe为力传感器反馈的机械臂末端力信号； JT机械臂雅可比矩阵的转置；Kfp和Kfi分别为比例增益与积分增益；CTH为力变换矩阵。

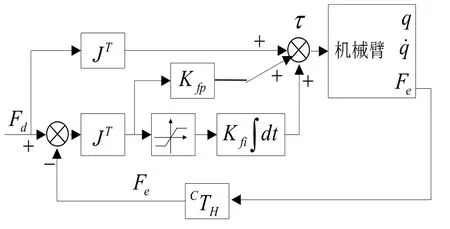
图2 机械臂力控系统结构图

3.2 平面二自由度机械臂的力控

在 Matlab/SimMechanics环境下对平面二自由度机械臂系统进行力控仿真与研究的思路为：在笛卡尔坐标系中，机械臂末端沿着圆的内侧（接触面）运动，在运动过程中，机械臂末端与圆内侧时刻保持接触，且相互作用力为一恒定值Fe（忽略机械臂末端与环境间的摩擦力）。为了保持机械臂的在运动过程中的平衡状态，必须对各个关节施加一定的驱动力矩τ（在此，平面二自由度机械臂的关节数恰与受控力的维数相匹配），根据式(5)可得所需施加的驱动力矩τ为：

其中，Fx和Fy是机械臂末端与外界相互作用的期望力Fe在笛卡尔坐标系上的分解，在机械臂运动过程中Fx和Fy时刻变化，合力Fe大小保持不变，方向为圆的法向且由圆心指向圆外，如图 3所示。

整个力控过程即为控制机械臂在一定时间内沿着一个圆的内侧运动，并保持在运动过程中，机械臂与圆内侧的相互作用力Fe为一恒定值。

图3 平面二自由度机械臂力控图

3.3 接触力模型

当机械臂末端与环境接触时，根据胡克定律，环境施加于机械臂的作用力Fe可作为弹性恢复力来模拟：

其中，矢量ΔXE表示由接触引起的环境局部变形，由图 4可知，当接触时 Δ XE=X-XE；当不接触时，ΔXE=0。KE描述环境的刚度。式(7)中忽略了摩擦力的作用，环境刚度KE和变形量ΔXE是方便又理想的表示方法，接触力Fe作为机械臂和环境集中变形来考虑，会更为准确。

图4 机械臂末端与环境接触模型

3.4 冲击振荡阶段的抑制控制

机械臂与刚性环境碰撞接触的过程可分为三个阶段：接近运动阶段、冲击振荡阶段、阻尼振荡阶段和稳定阶段[6]，如图 5所示。

图5 机械臂与刚性环境的碰撞接触过程

在机械臂与环境处于冲击振荡阶段时，两者之间将会产生一系列的脉冲力，如果脉冲力过大，必将会造成机械臂或环境的损坏。因此，需设计冲击振荡抑制控制器以削弱冲击振荡阶段的振动幅值，缩短冲击振荡持续时间。

冲击振荡阶段的抑制控制原理如图6所示，其中，图 6的（a）表示冲击振荡过程中机械臂末端的位置，虚线部分表示开环控制时的位置，实线部分表示通过抑制控制所期望达到的效果。图6的（c）表示向机械臂关节所提供的驱动力，整个抑制控制的过程即为依据机械臂末端位置的不同而改变关节驱动力的大小，最终实现振荡的抑制。图6的（b）为机械臂关节角速度-时间图，用来确定τmax与τd的切换时机，为切换的速度阈值。

图6 冲击振荡阶段的抑制控制

图 7详细给出了一个完整的振荡周期的抑制控制原理。ta、ts、tb、tc分别表示振荡周期的开始、驱动力切换、零速和振荡周期结束的时间。

图7 一个振荡周期的抑制控制原理

当t∈[ta, ts]时，对机械臂施加能提供的最大关节驱动力τmax，τmax=JTFe，Fe为反馈的机械臂末端的接触力，以此实现最大化的振荡抑制，降低后续振荡能量；当t∈[ts, tc]时，关节力矩则取较小的值τd，τmax=JTFd，Fd为期望的机械臂末端接触力，以此满足对期望接触力的控制。机械臂驱动力在τmax与τd之间切换，主要的依据是切换时间ts，分析冲击振荡过程可知，对ts的选取，需满足以下两个条件：

条件1：需保证当机械臂末端速度q˙(t)≥0(t∈[tb, tc])时，驱动力τmax必须停止作用从而减小机械臂恢复运动的速度。

条件2：尽可能长地增加τmax的作用时间，从而最大限度地削弱系统的振荡能量。

ts具体计算过程如下：

步骤 1：根据条件1，ts必须选在tb之前。如图 7所示，定义δt为tb与ts的时间差，且在tb时刻机械臂关节角速度q˙为0，则有：

其中，Jm为机械臂等效惯量。

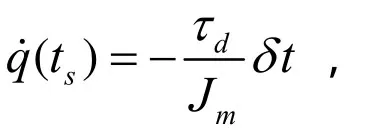
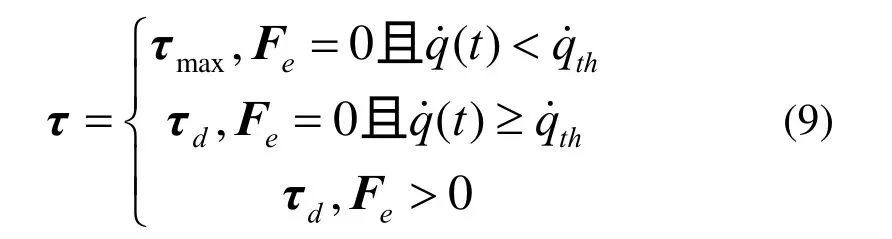
其中Fe为反馈的接触力，Fe=0表示未接触状态，Fe＞0表示接触状态。

4 平面二自由度机械臂的力控仿真与结果

4.1 SimMechanics仿真

在 Matlab/SimMechanics中搭建的平面二自由度机械臂力控系统如图 8所示，其中包括平面二自由度机械臂的机械模型、期望力、力传感器以及力控制器模块[8][9][9]。

图8 基于Matlab/SimMechanics的力控系统

平面二自由度机械臂的机械模型如图 9所示，其中，两个Revolute为转动副，表示机械臂的两个转动关节；两个 body表示机械臂的两个连杆，连杆的具体参数为：长度 l1=l2=0.35m ，质量m1=m2=0.747kg ，相对于 Z轴的转动惯量为IZ1=IZ2=0.0424kg*m2；Joint Sensor为关节传感器，其输出信号为关节的角度矢量q、角速度矢量以及角加速度矢量˙；Body Sensor输出信号为机械臂末端笛卡尔坐标系下的位置坐标x、y以及z，由于二自由度的机械臂只能控制二维方向上的位置或力，因此不对z轴数据做处理。

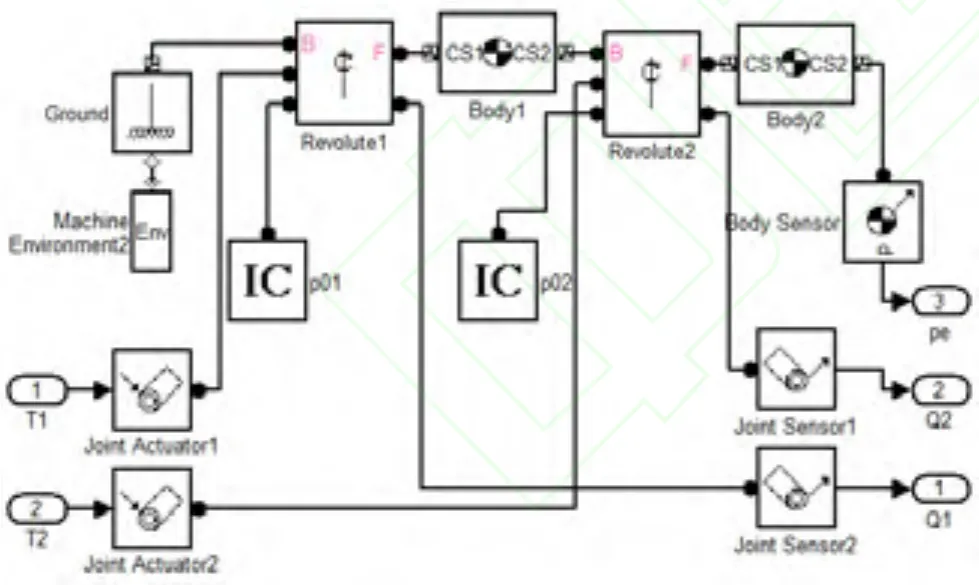
图9 基于SimMechanics的二自由度机械臂机械模型

根据式(7)，构造机械臂末端力传感器模型如图10所示，取环境刚度KE=80000N/m；ΔXE=X -XE，XE设为期望机械臂末端的运动轨迹，即为圆的半径，取R=XE=0.5m；X为笛卡尔坐标系下，机械臂末端在运动过程中与轨迹圆心的距离（为了简单起见，取轨迹圆心与机械臂第一个固定转动关节重合）。由式(7)可知，当机械臂与环境（即期望的轨迹）没有接触时，将不受到环境的外力；当机械臂与环境接触时，将产生相互的作用力Fe。这样就能够在平面中，模拟出机械臂与环境的接触面。

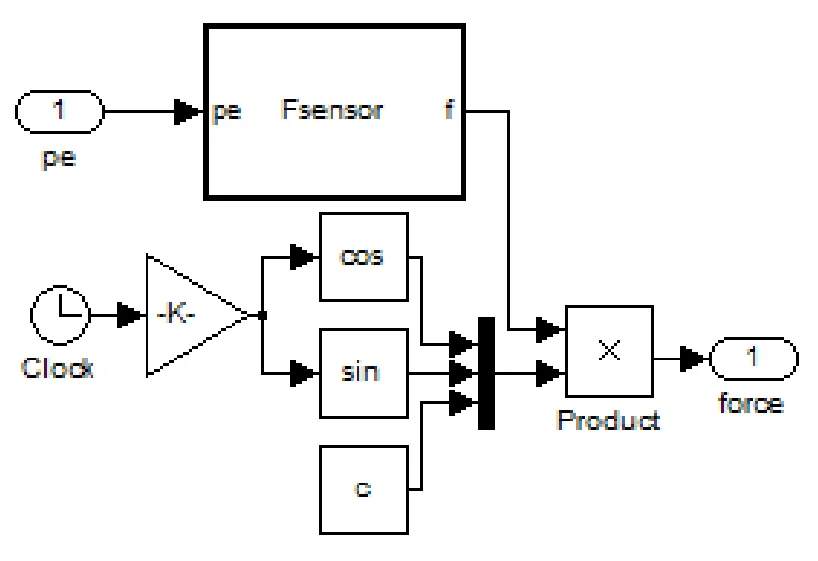
图10 基于SimMechanics的力传感器模型

机械臂末端期望的受力模型如图 11所示。在机械臂与环境接触前，给机械臂末端施加一个沿着接触面的法向，大小为8N的力Fe。在这个力的作用下，机械臂将向着期望的环境靠近，并最终与环境接触。在接触后，此期望力Fe即为机械臂与环境间相互作用的平衡力。

图11 基于SimMechanics的机械臂末端期望力模型

力控制器则是在Matlab中，将M文件嵌入到Simulink 仿真环境中，依据式(6)的机械臂动力学方程，对系统进行力控。同时，根据式(8)、(9)对机械臂与刚性环境碰撞接触过程中的冲击振荡阶段进行抑制控制。

4.2 仿真结果

具体的仿真结果如图 12、图 13、图 14、图 15所示。SimMechanics仿真环境中的平面二自由度机械臂的机械模型如图 12所示。

图12 基于SimMechanics的二自由度机械臂模型

机械臂末端的运动轨迹如图 13所示，通过对机械臂末端接触力的控制，实现了机械臂末端运动轨迹的规划。

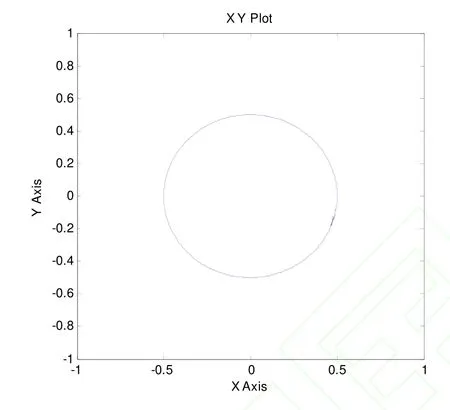
图13 机械臂末端运动轨迹

当未对碰撞接触过程中的冲击振荡阶段进行抑制控制时，机械臂末端与环境间的法向接触力如图 14所示。可见，机械臂与环境相接触时，特别是在冲击振荡阶段，两者之间产生一系列的脉冲力，相互间的碰撞相当剧烈，因此，有必要设计冲击振荡抑制控制器以削弱冲击振荡阶段的振动幅值，缩短冲击振荡持续时间。

图14 未进行冲击振荡抑制控制的法向接触力

对机械臂与环境碰撞接触过程中的冲击振荡阶段进行抑制控制后，机械臂末端与环境间的法向接触力如图 15所示。实例仿真结果表明，冲击振荡抑制控制器的使用，有效消弱了冲击振荡阶段的振动幅值、缩短冲击振荡持续时间。同时，在机械臂稳定运动的过程中，其末端与接触面之间的相互作用力保持为恒定的8N，很好的实现了特定作业下，机械臂与环境间接触力的控制。

图15 进行冲击振荡抑制控制的法向接触力

5 结论

本文主要研究了平面刚性二自由度机械臂与环境接触力的控制问题，在 Matlab/SimMechanics中建立力控系统的仿真模型，解决了机械臂力控过程中的一些问题：（1）机械臂力控作业的环境描述和运动建模；（2）在平面中模拟出机械臂与环境的接触面；（3）机械臂力控作业的力-运动轨迹生成；（4）实现机械臂末端执行器输出力以及关节力矩的控制；（5）实现机械臂与刚性环境碰撞接触过程中的冲击振荡阶段的振荡抑制。此后的工作将要实现平面刚性二自由度机械臂力-位混合控制，并将机械臂由二自由度扩展到多自由度，最终实现多自由度机械臂的力-位混合控制。

[1]D.E.Whitney.Resolved motion rate control of manipulators and human prostheses[J].IEEE Transactions on Man-Machine Systems, vol.10, pp.47–53, 1969.

[2]P.Fraise, F.Pierrot, P.Dauchez.Virtual environment for robot force control[J].IEEE 1993.219- 224.

[3]G.Afonso, J.N.Pires, and N.Estrela.Force control experiments for industrial applications:A test case using an industrial deburring example[J].Assem.Autom.J., vol.26, no.2, pp.148–156, 2007.

[4]F.L.Lewis, C.T.Abdallah, and D.M.Dawson, Control of Robot Manipulators[M].New York:MacMillan,1993.69-71.

[5]J.T.Wen.Position and Force Control of Robot Arms[J].Proc.IEEE International Symposium on Intelligent Control, Albany, New York, pp.251-256, September 1989.

[6]Nakju Lett Doh,Wan Kyun Chung,Youngil Youm,and Youngwhan Oh.Two Transition Phase Control Methods for Hard Contact[J].ASME Journal of Dynamic System,Measurement and Control, Vol 129, pp.262-274, May 2007.

[7]Yuan Shaoqiang, Liu Zhong, Li Xingshan.Modeling and Simulation of Robot Based on Matlab/SimMechanics[J].Proc.IEEE Symp.Control, IEEE Press,July 2008,pp. 161-165,doi:10.1109/CHICC.2008.4604913.

[8]Wenbin Deng, Jae-Won Lee, Hyuk-Jin Lee.Kinematics simulation and control of a new 2 DOF parallel mechanism based on Matlab/SimMechanics[J].Proc.IEEE Symp. Computing,Communication,Control,and Management(CCCM), IEEE Press,Aug 2010, pp.233-236.doi:10.1109/CCCM.2009.5267894.

[9]薛定宇, 陈阳泉.基于MATLAB/ Simulink 的系统仿真技术与应用[M].北京:清华大学出版社, 2002.