隐式GPC算法在重介分选过程控制中的研究
曹珍贯 ,匡亚莉
CAO Zhenguan1,2,KUANG Yali1
1.中国矿业大学 信电学院,江苏 徐州 221116
2.安徽理工大学 电气与信息工程学院,安徽 淮南 232001
1.School of Information and Electrical Engineering,China University of Mining and Technology,Xuzhou,Jiangsu 221116,China
2.School of Electrical and Information Engineering,Anhui University of Science and Technology,Huainan,Anhui 232001,China
1 引言
重介分选过程中,为保证分选产品的质量及稳定性,对分选过程的工艺参数实时检测与精确控制是十分必要的。重介分选的工艺参数有重介质悬浮液的密度、合介桶的液位、煤泥含量、入料压力等,而重介质悬浮液的密度是影响重介分选效果的关键参数,其控制精确稳定与否,直接决定重介分选的产品质量,因此重介分选的过程控制主要是对重介质悬浮液的密度控制[1]。近年来对重介质密度控制的研究很多,既有单变量控制又有多变量控制,即控制重介质悬浮液的密度或将密度与液位联合控制,现有的控制方法有PID控制和模糊控制[2]。文献[3]认为单纯用Fuzzy或PID控制效果都不理想,因而研究了Fuzzy-PID控制器,通过实际密度控制的数据对比,Fuzzy-PID控制的超调量和调节时间都比普通PID控制明显降低,动态特性改善,抗干扰能力强[3]。文献[4]中研究了重介选煤工艺介质密度和液位系统的动态特性,采用2个独立的模糊控制器,分别控制液位和密度,同时调节分流器和清水阀门,实现液位和密度控制,除此之外还有较多对重介分选过程控制的研究[4]。由于重介分选过程的工艺复杂性,密度与液位联调更能使密度输出稳定,但其控制对象的模型很难建立,且模型参数可能会随着生产过程发生变化,而上述控制方法未研究重介质过程模型失配情况下的控制效果。为解决控制过程中的模型失配问题,本文提出了利用隐式GPC算法,通过对重介分选系统的输入输出历史数据进行最小二乘辨识,实现求解系统模型参数,完成对重介质悬浮液的密度与液位多变量自校正解耦控制。

图1 介质控制示意图
2 选煤控制过程分析
选煤厂利用重介旋流器进行原煤分选,其介质流程示意图如图1所示,图中煤泥混合桶是将原煤与合格介质混合,通过入料泵把混料从煤泥混合桶打到重介质旋流器中进行分选,重介质旋流器的溢流进入脱介筛进行脱介,其介质通过分流箱一部分进入混料桶,一部分进入稀介质桶,稀介质桶的介质再经磁选机磁选后,送入合格介质桶,进行介质循环。在重介洗选过程中,控制参数主要有入料压力,重介质悬浮液的密度,煤泥含量等,其中合介桶中悬浮液的密度是控制分选产品质量的关键参数,因此必须保证合介桶中重介质悬浮液的密度稳定、控制准确[5]。重介质悬浮液的密度控制方法根据工艺不同而不同,本文利用加水及加介阀门来控制重介质悬浮液的密度与液位,分流箱用于控制合介桶中的煤泥含量。如图所示,合介桶中的输入量有:加水量、加介量、分流介质量及磁选机回流量,输出量为合介泵流量,其中分流介质量、磁选机回流量及介质泵流量在本系统中由于变化幅度较小,作为干扰量处理,因此加水阀门开度和加介阀门开度作为系统的控制量,合介桶中悬浮液的密度与液位作为被控量,假设加水阀门开度为U1,加介阀门开度为U2,合介桶液位为H,密度为ρ,则密度与液位控制系统的传递矩阵可表示为:

通过上式可见,合介桶中重介质悬浮液的密度与液位是一个两输入两输出耦合系统,必须实现解耦控制,本文利用多变量隐式GPC算法,实现重介质悬浮液的密度与液位的解耦控制。
3 隐式GPC控制算法
3.1 GPC算法原理
重介质密度控制系统的过程模型如式(1)所示,将该系统离散化,用CARIMA模型表示为两个独立的子系统[6]:
子系统1:
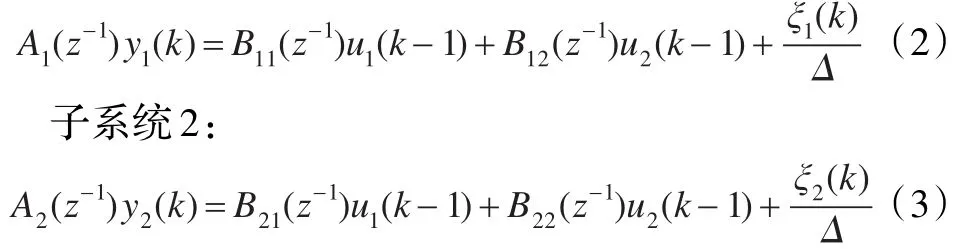
为求解最优控制增量序列,使系统的输出值能更逼近模型预测值,同时使系统输出紧密跟踪系统的设定值,其最优控制目标函数采用式(4)。

其中
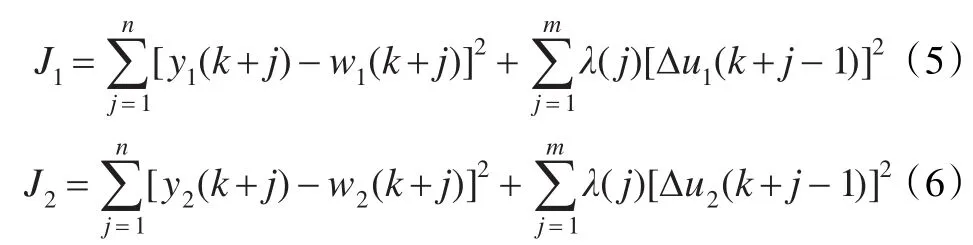
式中Δu为控制增量,W 为参考轨迹,Y为系统的实际输出,n、m分别为预测长度和控制长度,λ为控制加权系数,其中,w1、w2表达式为:
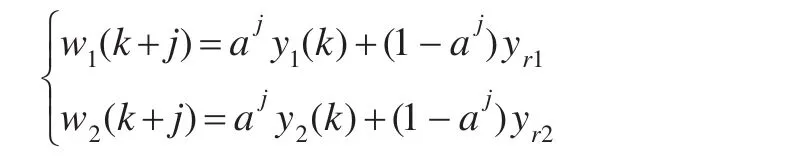
a表示柔化系数,yr表示系统的给定值。通过引入丢番方程图,可以求得两个子系统的最优控制律为[7-8]:
子系统1:

子系统2:

其中

从最优控制律的两个关系式来看,不难发现该系统虽然分解成两个子系统,但子系统1的控制增量和子系统2的控制增量分别对两个子系统的输出及目标函数是相互影响的,要使两个子系统成为真正的独立子系统,抛除子系统增量的耦合影响,必须对目标函数中的控制增量进行相应的处理。为了排除控制增量对输出预测的影响,本文用上一时刻的ΔU1值代替k时刻的ΔU1值,用上一时刻的ΔU2值代替k时刻的ΔU2值,使最优控制率中的 G12ΔU2、G21ΔU1变成已知量[9]。令=G12ΔU2+f1,=G21ΔU1+f2,则两个子系统的最优控制律可以表示为:
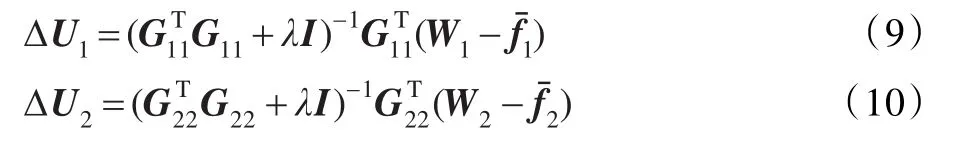
根据式(9)、式(10),只要计算出 G11、G12、G21、G22、f1、f2控制参数的值,则可以得到控制量U1和U2,在显式GPC算法中,上述参数是通过已知的系统模型参数进行计算的,当模型失配时,必须及时调整控制参数,使控制效果最佳,因此本文通过最小二乘法实现控制参数的在线辨识。
3.2 控制参数的自校正辨识
根据最优控制律的目标函数,求解出最优控制增量解,对于子系统1而言,其控制增量方程为式(9):从上式可知,要求ΔU1必须知道矩阵G11、G12和开环向量 f1的值,其中控制增量的加权因子λ和经柔化器处理后的设定值向量w1是已知量,控制参数自校正方法就是利用系统的输入输出数据,根据预测方程直接辨识求解G11、G12和开环向量 f1。
以子系统1为例,根据子系统1的预测输出方程式可得到n个并列预测器为[10]:
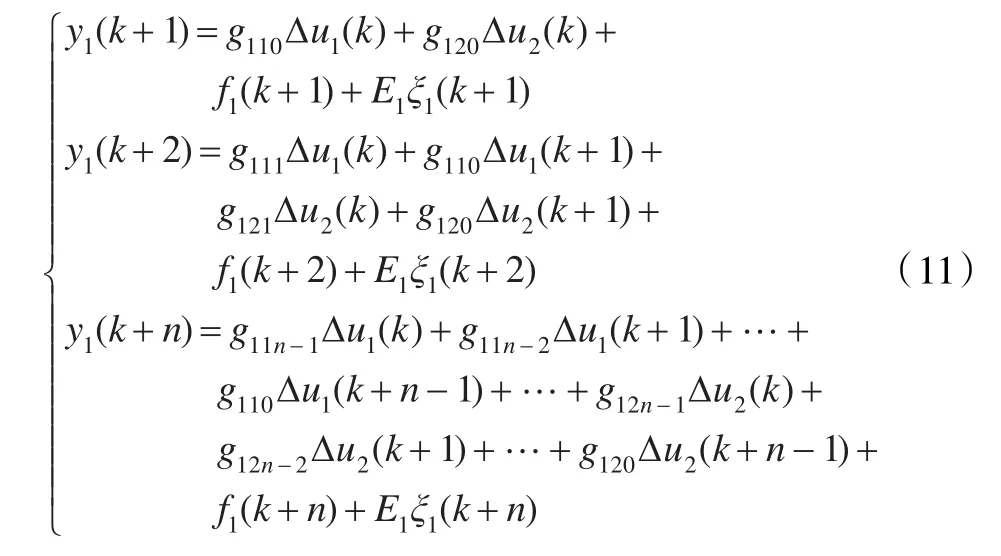
分析上式可知,矩阵G11、G12中所有元素都在最后一个方程式中出现,因此,只需对最后一个方程进行参数辨识,便可求解矩阵G11、G12。
由式(11)最后一个方程用向量形式表示:

其中
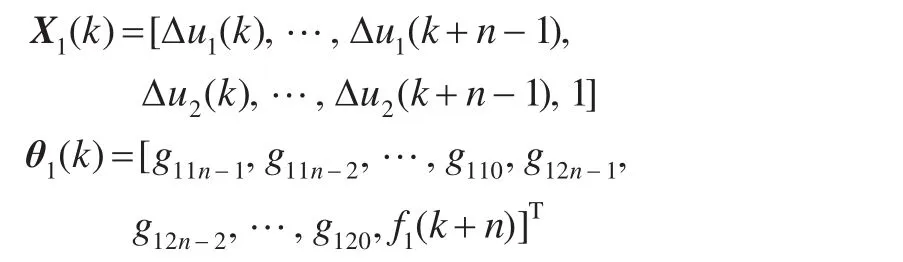
因此输出预测值可表示为:

在k时刻,若 X1(k-n)的元素值已知,Enξ1(k+n)为白噪声,参数向量θ1(k)则能用最小二乘法进行估算,然而通常Enξ1(k+n)不是白噪声,因此本文将采用控制策略与参数估算相结合的方法,即用忽略噪声的输出预测值 y^1(k|k-n)来代替输出预测值 y1(k|k-n),并认为y^1(k|k-n)和实际的输出值 y1(k)的差值为白噪声ε1(k)[11]。由此得出:

θ1(k)通过最小二乘递推法进行求解:

上式中,λ1为遗忘因子,0<λ1<1。通过系统的输入输出数据利用上述递推公式进行求解,可得到θ1(k)的估计值,即可得到矩阵G11、G12的参数,同理可得到G21、G22的参数。
在得到矩阵G的参数后,还需要求解预测向量 f的值,通过参考文献[3]中关于GPC与DMC控制规律的等价性,可知GPC中的 f1向量与DMC中的Y10向量等价,因此可得到下一时刻的Y10向量为:

式中 p 为模型时域长度(p≥n),h12,h13,…,h1p为误差校正系数。e1(k+1)=y1(k+1)-y1(k+1/k)为预测误差,在这里取h12=h13=…=h1p=1。由于 f1与Y10的等价性,可得到下一时刻的预测向量 f1为:

通过上述求解,便可计算G11、G12和 f1的值,再利用式(9)则能计算子系统1的控制增量;同理,利用同样的方法,可计算 G21、G22和 f2的值,再利用式(10)则能计算子系统2的控制增量,因此通过上述方法能够实现GPC控制参数的在线校正。
4 仿真测试
根据现场的阶跃响应数据,重介质悬浮液密度与液位过程数学模型如式(18)所示。

计算该过程模型的相对增益为:

根据式(18)、式(19)可以看出,重介质悬浮液密度与液位是一个大滞后的强耦合控制系统[12-13],取采样周期T为5 s,采用双线性变换法将式(18)离散化,得到离散化后的表达式为:
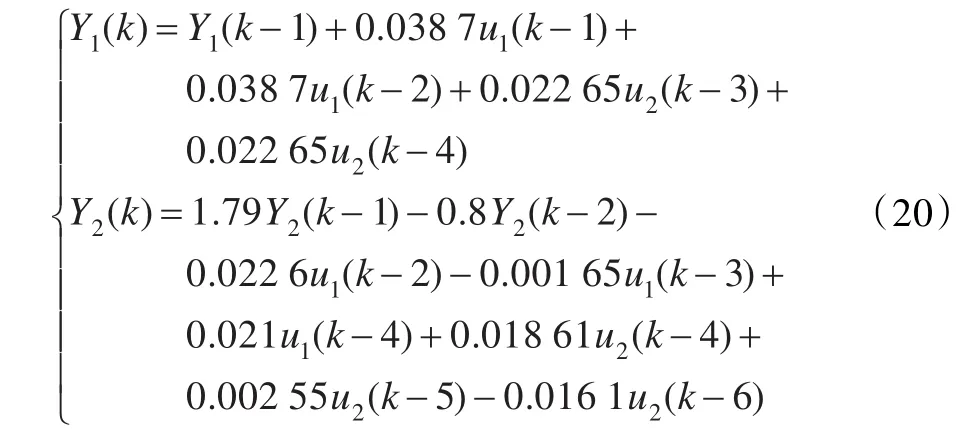
假设合介桶中重介质悬浮液的液位初值为2 m,密度初始值为1 kg/L,要求将液位控制在3.5 m,密度控制在1.45 kg/L,利用隐式GPC算法进行仿真。在仿真过程中设时域长度为9,预测长度为9,控制长度为3,加权控制系统为0.8,柔化系统数为0.1。为检验隐式GPC算法控制效果,整个仿真过程将与模糊PID算法控制结果进行比较,以下仿真效果图中绿色点线表示模糊PID控制曲线,红色实线表示隐式GPC控制曲线。在不增加干扰、模型参数不变的情况下,其仿真运行如图2所示。

图2 重介质悬浮液隐式GPC控制效果图
图2中所示两种算法均能使液位和密度在经历振荡与超调后趋于系统的给定值并保持稳定,其中模糊PID对液位的控制效果较好,超调小,响应快,而隐式GPC对密度控制效果较好。为检验两种算法的抗干扰能力,在系统运行中,对液位输出加入0.1的随机干扰,对密度输出加入0.01的随机干扰,其仿真运行效果分别如图3、图4所示。

图3 液位输出干扰下系统控制仿真效果图
对比上述控制效果图可以看出,液位干扰影响大于密度干扰,加入干扰后,延迟了系统的稳定时间,同时系统的超调也增大,但最终液位与密度都很快趋于稳定。相比隐式GPC算法而言,无论液位干扰,还是密度干扰,模糊PID的输出振幅要大于隐式GPC算法,后者的输出曲线较为光滑,因此隐式GPC控制算法对系统的抗干扰能力强,控制效果较好。为检验两种算法对模型的精确度要求,在系统运行中,对系统的模型参数进行调整,分别修改重介质悬浮液控制过程模型中G11、G21的增益系数,其运行仿真分别如图5、图6所示。

图4 密度输出干扰下系统控制仿真效果图

图5 调整G11增益系统控制效果仿真图

图6 调整G21增益系统控制效果仿真图
通过上述两图可以发现,无论对G11还是G21的增益参数调整,重介质悬浮液的液位与密度都能在振荡后趋于稳定,并紧跟参考值。但模糊PID算法在模型失配的情况下,系统的振荡加强,使输出稳定时间延长,而隐式GPC算法的输出相对平滑、超调小,且响应速度较快,不存在系统不能稳定或振荡输出的情况,这是得益于被控对象的模型参数是通过系统的输入输出数据利用最小二乘法进行计算的,其模型是根据实际数据计算产生,并实时更新的,另外控制量的输出经过加权约束处理,因此基于隐式GPC算法对重介质悬浮液液位与密度解耦系统的控制效果较好。
5 结论
综上所述,可以发现隐式GPC重介质密度解耦控制算法,在密度与液位的响应存在大滞后、强耦合的情况下,抗干扰能力强,能根据输入输出进行控制参数自适应调整,保证重介质悬浮液的密度与液位输出能够实时追踪系统给定值;特别在模型失配的情况下,响应速度快,超调小,输出平滑,控制性能好于模糊PID算法,因此隐式GPC算法对重介质悬浮液的密度与液位有着良好的解耦控制效果。
[1]赵春祥,叶桂森.重介质选煤过程控制模型及控制算法的研究[J].煤炭学报,2000(12):196-200.
[2]胡娟,王振翀,王福忠.基于模糊控制理论的重介质选煤过程控制[J].煤炭科学技术,2011,39(3):116-119.
[3]孟凡芹,王耀才,姜建国,等.重介工艺悬浮液密度和液位的多变量模糊控制方法研究[J].中国矿业大学学报,2005,34(2):252-255.
[4]王海,李艳娟,巩亚东,等.基于plc的fuzz-Pid分选密度控制研究[J].控制工程,2006,13(5):474-477.
[5]王波,张致维,王然风.重介浮选液密度自动控制系统的设计[J].控制工程,2011(S1):69-71.
[6]Clarke D W,Mohtadi C,Tuffs P S.Generalized predictive control-part1:basie algorithm[J].Automatiea,1987,23(2):137-148.
[7]李国勇.智能预测控制及其MATLAB实现[M].北京:电子工业出版社,2009.
[8]李灿军,彭辉.液位系统的多模型广义预测控制研究[J].计算机工程与应用,2011,47(27):236-238.
[9]师五喜.广义预测控制中dioaphantine矩阵多项式方程的显式解[J].控制理论与应用,2007,24(2):261-263.
[10]朱学莉,齐维贵,邵仙鹤.供热过程GPC隐式自适应算法应用研究[J].哈尔滨工业大学学报,2005,37(2):227-232.
[11]Gorazd K,Igor S,Borut Z.Self-adaptive predictive functional control of the temperature in an exothermic batch reactor[J].Chemical Engineering and Processing,2008,47(12).
[12]李国勇.过程控制系统[M].北京:电子工业出版社,2009.
[13]郭西进,高警卫,沈磊,等.重介选煤工艺多参数的模糊解耦控制研究[J].选煤技术,2012(3):79-82.

