萤火虫算法优化最大熵的图像分割方法

吴 鹏

WU Peng

淄博职业学院，山东 淄博 255314

Zibo Vocational Institute,Zibo,Shandong 255314,China

1 引言

图像分割是指根据一定的分割原则，把图像分割成若干感兴趣的区域，是图像处理的关键和首要步骤，其分割结果优劣直接影响人们对图像的理解和使用，因此图像分割是计算机图像研究的热点和重要课题[1]。

针对图像分割问题，国内外学者进行了大量的研究，提出了许多行之有效的分割方法，主要分为：区域增长法、边缘检测法和阈值法等几类分割方法[2-4]。阈值法具有简单，易实现，性能稳定等优点，成为目前使用最为广泛的图像分割方法，其主要包括最大熵法、最大类间方差法、最小误差阈值法等[5-8]，其中最大熵法对目标大小不敏感，可用于小目标的图像分割，且对不同目标大小和信噪比的图像可以获得较好的分割效果，但最大熵法是通过使分割后图像的熵最大化实现图像分割，因此最佳阈值的选择，对分割效果起着决定性的作用[9]。传统最大熵法采用遍历全部灰度级来寻找最优阈值，计算量大、耗时长、速度慢，尤其对复杂图像进行多阈值分割时，计算复杂度增加，难以满足图像分割的实时处理要求[10]。为了解决最大熵法的最佳阈值选择问题，一些学者提出采用粒子群优化算法、遗传算法对最佳阈值进行优化，一定程度上提高了图像分割效果，但是它们均不能克服易陷入局部最优、早熟等弊端，图像分割精度有待进一步提高[11-12]。2008年，Yang Xinshe提出一种新型的仿生智能算法——萤火虫算法（Firefly Algorithm，FA），其具有简单、参数少、收敛迅速等优点，在组合优化领域得到了较广泛应用，为最大熵法的最佳阈值选择问题提供了一种新的研究工具[13]。

为了提高图像的分割精度，提出一种基于萤火虫算法优化最大熵的图像分割方法。首先获得最大熵法的阈值优化目标函数，然后采用萤火虫算法对目标函数进行求解，找到图像的最佳分割阈值，最后根据最佳阈值对图像进行分割，并通过仿真实验对分割效果进行测试。结果表明，本文方法可以迅速、准确找到最佳阈值，提高了图像分割的准确度和抗噪性能，可以较好地满足图像分割实时性要求。

2 最大熵法和萤火虫算法

2.1 最大熵法

最大熵法目的是将图像灰度直方图分成独立的类，使得各类熵之和达到最大值。对于灰度图像来说，信息熵越大则表示图像区域的灰度值分布越均匀。将Shannon熵概念应用于图像分割时，依据是使图像中目标与背景分布的信息量最大，通过分析图像灰度直方图的熵，找到最佳分割阈值[14]。

采用一灰度值t(0＜t＜L-1)将图像中的像素按灰度级划分成2类C0和C1，C0表示目标对象，C1表示背景，即 C0={0，1，…，t}，C1={t+1，t+2，…，L-1}，则 C0和C1对应的灰度值概率归一化分布分别为：

令 pc0(k)=pk/PD0，k=0,1,…,t，pc1(m)=pm/PD1，m=t+1，t+2，…，L-1，那么，C0和C1的熵分别为：

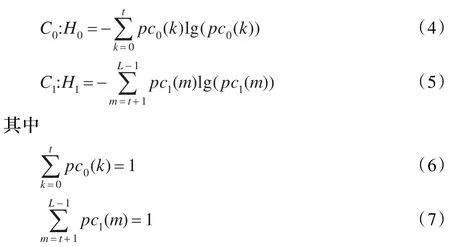
图像的后验熵之和为：

当熵函数H取得最大值时所对应的灰度值为T时，就是所求的最佳分割阈值，即

阈值确定是最大熵法图像分割的关键，采用传统穷举法在全灰度范围内搜索最佳阈值十分耗时，无法满足图像分割对实时性的要求，为此，本文采用萤火虫算法对最大熵法的最佳阈值进行搜索求解。

2.2 萤火虫算法

萤火虫算法（FA）是一种模拟自然界中萤火虫发光行为的仿生智能算法，其利用萤火虫的发光特性，在指定区域内搜索同类并向较优个体的区域靠近，从而实现位置寻优[15]。每个萤火虫被称为一个个体，个体主要有位置、亮度、吸引度等属性，萤火虫之间相互吸引有两个影响因素：亮度和吸引度，亮度的大小与萤火虫所处的位置相关，位置越好亮度越大；吸引度与亮度相关，吸引度高的萤火虫具有更大的概率吸引其他个体向其位置靠近。在FA开始，萤火虫的位置随机地分布于指定区域内，个体的亮度I由目标函数值所处位置决定，其他个体所能接收的亮度除了受其固有亮度影响外，还与两个体之间的距离以及传播介质的吸收率有关，距离越远，能接收到的亮度越弱。设I0表示萤火虫的最大亮度，γ为介质的光强吸收系数，rij为任意个体i和 j的相对空间距离，则两个体的相对亮度为：

那么两个体间的相对吸引度β为：

式中，β0为最大吸引度（rij=0处）。

分别用xi、xj表示萤火虫个体i和 j的空间位置，α为步长因子，rand为[0，1]上服从均匀分布的随机因子，则个体i被吸引度较大的个体 j吸引，向其靠近的位置更新公式为：

3 萤火虫算法选择最大熵法的图像分割阈值

（1）初始化FA的参数，主要包括萤火虫数目D，光强吸收系数γ，最大吸引度β0，步长因子α，最大迭代次数Nmax。

（2）计算图像灰度值对应的像素数量和灰度值的概率，以及图像的灰度值期望，并确定出最佳分割阈值的取值范围。

（3）随机初始化各萤火虫的位置，其代表最大熵法的最佳分割阈值，并根据式（9）计算目标函数值，并化为相应个体的最大亮度I0。

（4）对各萤火虫个体进行两两比较，吸引度较弱的向较强个体靠近，按照公式（12）进行位置更新，对处于较优位置上的个体则进行随机扰动。

（5）对位置更新后的萤火虫重新计算亮度，并对较优个体进行基于互换操作的局部搜索，当目标值得到改善时，则替代原有排序，否则维持原来的最优解。

（6）当达到最大迭代次数 Nmax，记录此时的最优解，否则，重复步骤（4）、（5）进入下一次搜索。

（7）根据最优解得到全局最优的图像分割阈值。

4 仿真实验

4.1 图像来源及仿真环境

图1 实验图像

为了测试本文图像分割方法性能，选择三种类型的Lena图像作为仿真对象，具体如图1所示。仿真实验均在 Intel®CoreTM2.5 GHz CPU，4 GB RAM，Windows XP操作系统平台，采用VC++编程实现。

4.2 结果与分析

4.2.1 分割结果的视觉效果评价

选择传统最大熵法、最大类间方差法、最小误差阈值法和粒子群优化最大熵值法进行对比实验，它们的分割结果如图2～4所示。对图2～4的分割结果进行分析，可以得到如下结论：

（1）传统最大熵法采用穷举法搜索最佳阈值，取得了较好的分割效果，但要求适合搜索目标和背景内部的灰度分布尽可能均匀的情况，当图像存在一定量的噪声时，分割效果不好。

（2）最大类间方差法是一种依据均匀性度量的最佳阈值方法，对于信噪比高图像可以获得十分理想的分割效果，然而对信噪比低图像分割的小区域过多，产生了严重的过分割现象，分割效果不理想，应用局限性较强。

（3）最小误差阈值法抗噪能力比较差，当图像含有噪声时，选择的分割阈值比较大，导致将目标错判断为背景，形成区域间的空洞，分割效果不理想。

（4）粒子群优化最大熵值法的图像分割结果要优于传统最大熵法、最大类间方差法、最小误差阈值法，这表明通过粒子群优化算法可以找到较优的分割阈值，获得更加理想的分割结果。

图2 Lena原始图像的分割结果

图3 高信噪比图像的分割结果

图4 低信噪比图像的分割结果

（5）相对于传统最大熵法、最大类间方差法、最小误差阈值法，本文方法分割效果显著提高，分割更细微，对不同信噪比的图像鲁棒性较好，提高了图像分割的准确度和抗噪能力，适用范围更广；同时相对于粒子群优化最大熵值法，本文算法的分割结果更优，这主要是由于萤火虫算法较好地克服了粒子群算法易陷入局部最优、早熟等弊端，图像分割精度得到了进一步提高。

4.2.2 分割结果的客观评价

在评价图像分割方法性能时，有许多客观评价标准，本文采用区域间对比度和区域内部均匀性测度对分割结果好坏进行定量分析。

（1）区域间对比度（GC）是指根据区域间的对比度衡量图像的分割质量，即

式中，f1和 f2分别为两个区域的平均灰度值。

（2）分割图像的区域内部均匀性测度（UM）为：

式中，Ro为分割图中的第o个区域；Ao表示第o个区域像素个数；C为归一化参数；f(x，y)为(x，y)点的像素值。

（3）综合测度

式中，λ1和 λ2为权值，λ1+λ2=1，综合测度的值越大，分割效果越好。

表1为几种方法的最佳分割阈值，从表1可知，当图像含有噪声时，对比方法的分割阈值相对较大，出现了一些过分割现象，不能根据图像质量进行自适应变化，而本文通过采用萤火虫对阈值进行自适应调整，获得了比较合理的分割阈值。

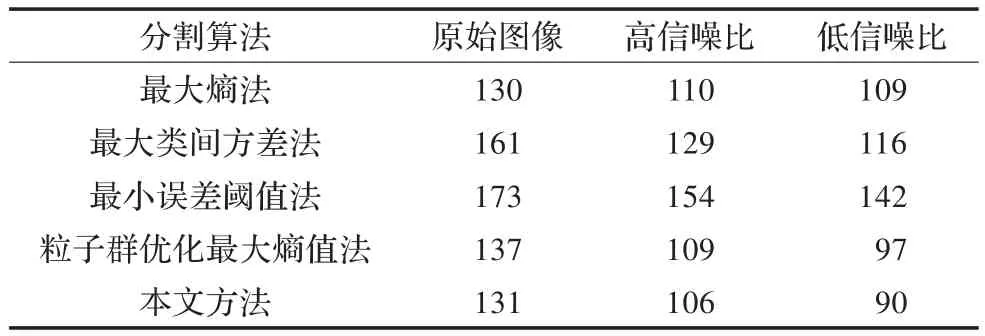
表1 几种方法分割性能比较

不同分割方法的区域间对比度值和区域内部均匀测度值如表2和表3所示。据区域内部含有细节信息的多少，设定综合测度，λ1=0.2，λ2=0.8，不同方法分割所对应的综合测度值如图5所示。从图5可知，相对于对比方法，本文方法的综合测度值提高相当显著，对比结果表明本文方法的图像分割精度更高、效果更好。

表2 不同分割方法的区域间对比度值

表3 不同分割方法的区域内部均匀测度值

图5 不同方法分割结果的综合测度值

4.2.3 分割速度的比较

对于图像分割应用来说，速度至关重要，采用分割时间作为分割速度的评价标准，几种方法平均分割时间（s）如图6所示。从图6可知，传统最大熵法的平均分割时间最长，主要是由于其采用穷举法对阈值进行搜索，计算复杂，耗时多；粒子群算法的平均分割时间要优于传统最大熵法、最大类间方差法、最小误差阈值法，但是要多于本文方法，这主要是由于本文方法利用萤火虫的全局搜索能力，最佳阈值的搜索时间大幅度下降，计算复杂度小，提高了图像分割速度，可以较好地满足图像分割实时性要求。

图6 不同方法的分割速度对比

5 结束语

针对传统最大熵法存在分割时间长，计算复杂度较大等缺点，提出了一种基于萤火虫方法优化最大熵阈值的图像分割方法。该方法基本思想为：由最大熵法得到目标函数，用萤火虫算法对目标函数进行优化，来搜索图像分割的最佳阈值，最后用搜索到的阈值对图像进行分割。仿真结果表明，本文方法提高了图像分割的准确率和分割速度，且具有鲁棒性高等优点，在图像分割具有广泛的应用前景。

[1]Sezgin M，Sankur B.Survey over image threshold techniques and quantitative performance evaluation[J].Journal of Electronic Imaging，2004，13（1）：146-168.

[2]郑丽萍，李光耀，姜华.灰度图像最大熵分割方法的改进[J].计算机工程与科学，2010，32（12）：53-56.

[3]沙秀艳，辛杰.基于最大熵的模糊核聚类图像分割方法[J].计算机工程，2011，37（10）：187-191.

[4]梁建慧，马苗.人工蜂群算法在图像分割中的应用研究[J].计算机工程与应用，2012，48（8）：194-196.

[5]Jiang Frank，Frater M R，Pickering M.Threshold-based image segmentation through an improved particle swarm optimization[C]//2012 International Conf on Digital Image Computing Techniques and Applications，2012.

[6]范九伦，赵凤.灰度图像的二维Otsu曲线阈值分割法[J].电子学报，2007，35（4）：751-755.

[7]唐新亭，张小峰，邹海林.图像分割的最大熵方法的改进[J].计算机工程与应用，2012，48（1）：212-215.

[8]Wan Y，Yao L，Xu B G.Automatic segmentation of fiber cross sections by dual threshold[J].Journal of Engineered Fibers and Fabrics，2012，7（1）：114-120.

[9]童成意.基于种内协同克隆选择的Otsu图像分割算法[J].计算机工程与应用，2013，49（24）：161-164.

[10]刘艳林，马苗，刘艳丽，等.基于改进人工鱼群算法的含噪图像分割方法[J].计算机工程与应用，2013，49（20）：157-160.

[11]高业文，熊鹰，潘晶晶，等.基于IGA与GMM的图像多阈值分割方法[J].计算机应用研究，2012，29（3）：1130-1135.

[12]王树亮，赵合计.基于改进粒子群算法的多阈值灰度图像分割[J].计算机应用，2012，32（S2）：147-150.

[13]Yang Xinshe.Improved firefly algorithm approach applied to chiller loading for energy conservation[J].Energy and Buildings，2013，59（10）：273-278.

[14]刘健辰，沈洪远.基于微粒群算法的二维最大熵图像分割算法[J].计算机工程与应用，2007，43（35）：102-104.

[15]吴斌，钱存华，倪卫红.萤火虫群优化算法在越库调度问题中的应用[J].计算机工程与应用，2013，49（6）：39-42.