Laguerre谱方法在地震勘探中的应用
闵涛,任菊成,邢星
MIN Tao,REN Jucheng,XING Xing
西安理工大学,理学院,陕西 西安 710054
School of Science, Xi’an University of Technology, Xi’an 710054,China
引言
地震勘探[1-2]是利用地下介质弹性和密度的差异,通过观测和分析大地对人工激发地震波的响应,推断地下岩层的性质和形态的地球物理勘探方法。它是钻探前勘测石油与天然气资源的重要手段,在煤田和工程地质勘查,区域地质研究和地壳研究等方面得到广泛的应用.地震勘探的深度一般从数十米到几千米不等.如果假设地层是横向均匀的,且震源力只沿纵向分布,则地震波传播近似的被描述为如下的一维波动方程定解问题

其中u(x, t)表示质点震动的速度,f(x, t)为震源函数,ρ(x)为介质密度,k(x)为弹性系数,T为地面记录的最大时间,L为所要研究的最大深度.x轴指向地下方,即x为深度.在地表x=0处,我们可接收到反射长波

地震勘探的任务就是根据就是根据方程(1)和测量条件(2)反演地震参数ρ(x)和k(x).对此问题已经有一些文献对其进行了研究,文献[3]张大力等人利用正则迭代法对k(x)进行了参数反演,文献[4]张丽琴利用同伦方法进行了波阻抗反演等,它们更多关注于参数反演的方法而对正问题的研究关注较少,然而我们知道,要求反问题必须先解决正问题,对于正问题,不同的解决方法自然影响反演的精度.因为仅根据g(t)便要同时进行双参数反演是不可能的,因此本文假定介质密度ρ(x)和弹性系数k(x)部分信息已知,且主要研究深度L较大时的情况,比如L=500千米,以米为单位,这时我们可以近似的将问题看作为定义在[0,∞)上的问题.对此用无界区域上的正交多项式(函数)直接在无界区域上进行逼近求解.关于这方面的详细介绍可见综述性文献[5-8].而无界区域上的谱方法便是一种很好的解决方案,例如Hermite谱方法[9-10]和Laguerre谱方法[11-14],这是因为谱方法具有很高的精度,它有助于我们获得更加准确的反演结果.
本文主要从大深度地震勘探一维波动方程[15-18]出发,首先采用 Laguerre谱方法对其正问题进行研究,给出了求解的离散过程,然后用高斯-牛顿法对其进行参数反演并通过仿真进行了数值模拟.
1 Laguerre谱方法
对于半无界区域上的问题,这里选择用Laguerre谱方法,为了获得差分矩阵,首先利用谱配置法,它是一种基于权函数的插值,形式如(3)式:
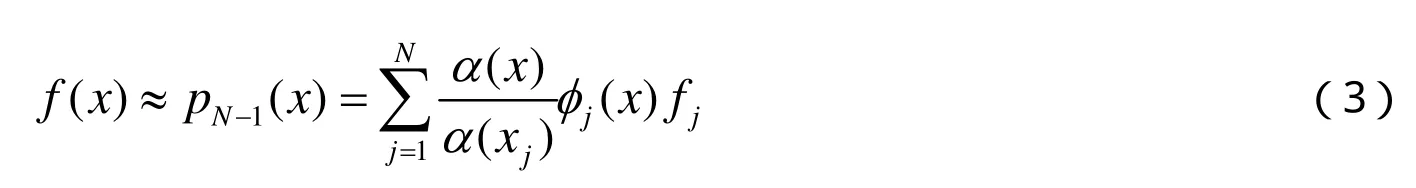
也就是说pN-1(x)作为f(x)的一种插值,有(4)式成立:

对(1)式,在各节点xk处求n阶导数可得(5)式:

导数的求解用一个矩阵(n)D 表示,则可推导出(6)式:

故而数值差分过程如下:

其中,f为函数在各节点xk处的函数值,f(n)为函数在各节点xk处近似得到的导数值。求解微分方程时,导数通过(7)的离散求导去近似.对于 Laguerre谱方法,我们取 x1=0,x2…xN为LN-1(x)的根,其中LN-1(x)为Laguerre 多项式(关于权函数α(x)=e-x2正交),N-1为Laguerre多项式的次数:

权函数为α(x)=e-x/2,则插值函数为:
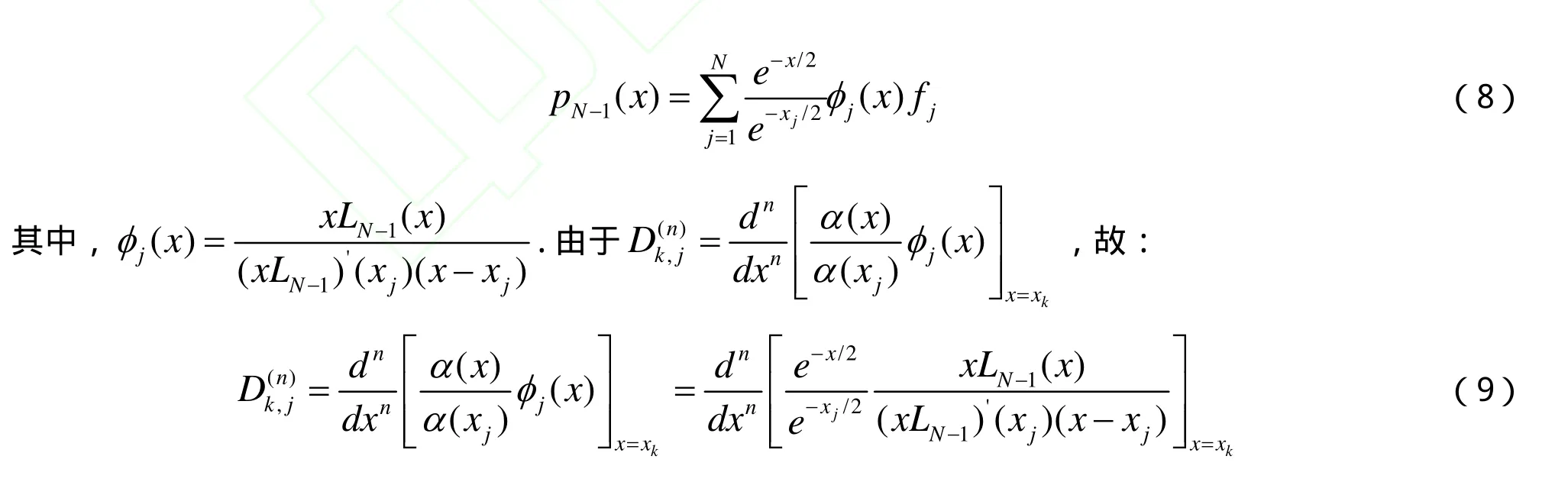
这样我们便获得了n阶的Laguerre谱差分矩阵.

其中k'(x)为k(x)的导数(这里只考虑k(x)可导的情形),对空间变量进行Laguerre离散得m阶导数:


其中,D(1),D(2)分别为一阶,二阶 Laguerre谱差分矩阵,这样方程(1)变成了(11)和(12)组成的常微分方程组:


2 仿真实验


图1 u(x, t)的近似解Fig 1 The approximate solution of u(x, t)

图2 u(x, t)的真解Fig 2 The true solution of u(x, t)

表1 不同时间点处真解与近似解的误差Table 1 The error of true solution and approximate solution at different time points

0.6 9.544235569643507e-015 1.555719199907700e-014 0.7 1.089865647698605e-014 1.305177103030653e-014 0.8 1.186760807613160e-014 1.088117471906690e-014 0.9 1.308203817152395e-014 9.477263496488302e-015 1 1.418303078577562e-014 8.322649553556040e-015 CPU时间(秒) 0.119568
从以上我们可以看出,此方法对于求解此类问题具有非常高的精度且计算速度较快.
有了高效的正问题求解,下面将由方程(1)和测量条件(2)反演地震参数ρ(x)和k(x).显然仅根据g(x)便要同时进行双参数反演是不可能的.因此本文假定密度为 ρ(x)=x+a1,弹性系数为k(x)=x2+a2x ,其中a1, a2是需要反演的参数,为了验证方法的有效性,首先给出参数真值a1=1,a2=0.5,可通过求解正问题得 u(0,t)=g(t),并把它作为附加条件来反求参数 a1,a2,其中g(t)=t2.设 u(0,ti)是在地面接收到反射长波,u(0,ti, a1, a2)是以a1, a2为参数解正问题所得的计算结果,则参数反演问题转化为如下非线性优化问题

采用高斯-牛顿法求解,具体步骤如下:


第三:为了避免求解的不稳定性,利用正则化方法,将方程组转化为(ATA+αI)·Δ=ATG来求解σi,进而得到当σi值较大时,可令当前的ai值代替原来的近似值,重复上述过程,得到新的σi(进而得ai).这种过程可以反复迭代,直到指定的迭代次数为止.
由于在实际问题中,接收到的反射波会受到各种因素的影响,所以对条件(2)施加干扰,如=(1+δrand(1))g(t),我们取初时猜测(a1, a2)=(0.1,0.1),参数α=0.03,σ=0.0001,迭代100次,δ取不同值时计算结果如下(真解为:(a1, a2)=(1,0.5)):

表2 不同程度干扰反演结果Table 2 The inversion results of different degree interference
计算结果表明:(1)当地面记录g(t)含一定噪声时,反演结果与真实速度的吻合程度非常好,其相对误差几乎可以忽略.从迭代过程来看,虽然要反演的有2个数,但用该方法只需要很短时间就可以找到全局极小点,当然如果迭代次数更多的话,反演结果会更接近真解.(2)虽然随着噪声水平的增加,反演结果的精度有所降低,但由上面的计算结果可以看出,反演结果仍是令人满意的,这说明该方法具有一定的抗噪能力.
3 结论
针对大深度地震勘探问题,本文首先采用Laguerre谱方法对其正问题进行研究,给出了求解的离散,然后用高斯-牛顿法对其进行参数反演并通过仿真进行了数值模拟.结果表明这种方法对于大深度地震勘探具有较好的效果.
[1]戴向峰 .姜太亮 郑晓英 星全玲.地震勘探方法及应用-地震属性分析[J].青海石油.2011,29(3):13-17
[2]马在田等编著,计算地球物理学概论[M].同济大学出版社,1997
[3]Huang G Y.An algorithm for processing seismic exploration data .Chinese J.Geophys(in Chinese), 1985,28(1):74-83
[4]张大力,吴建成,刘家琦.一维波动方程反问题求解的正则迭代法 [J].计算物理, 2000,17(3):326-330.
[5]张丽琴,王家映,严德天.一维波动方程波阻抗反演的同伦方法 [J].地球物理学报, 2004,47(6):1111-1117.
[6]Jie Shen and Lilian Wang.Some recent advances on spectral methods for unbounded domain [J].Commun.Comput.Phys,2009,5(2-4):195-241
[7]Jie Shen.Stable and efficient spectral methods in unbounded do mains using laguerre functions[ J].SIAM J.NUMER.ANAL, 2000, 38(4) :1113~ 1133.
[8]B.Y.Guo and J.Shen.Laguerre-Galerkin method for nonlinear partial differential equations on a seminfinite interval[ J].Numerische Mathematik, 2000,86(4) :635~ 654.
[9]V.Iranzo and A.Falques.Some spectral approximations for differential equations in unbounded domains[ J].Comp.Meth.in Appl .Mech and Eng, 1992, 98:105-126.
[10]王中庆.无界区域问题的有理谱方法[ D].上海:上海大学,2002.
[11]张璟,无穷域问题的谱方法研究[D]上海大学:上海大学博士学位论文.2003
[12]王冲,无界区域问题的Laguerre谱方法 [J].山东理工大学学报(自然科学版)2010,24(6):85-87.
[13]叶小华.四阶方程的Legendre-Laguerre复合谱方法[J].吉林师范大学学报(自然科学版).2009,5(2):121-128
[14]徐承龙,郭本瑜.多维区域中非线性偏微分方程的修正 Laguerre谱与拟谱方法[J].应用数学和力学.2008,29(3):281-300
[15]Han B, Yang X J, Liu J Q.Differential continuation-regularization method and the coefficient inverse problem of one-dimensional wave equations.Applied Mathematics-A Journal of Chinese Universities(in Chinese) , 1994, 9(A4) :351~ 360
[16]刘家琦,刘克安等.微分方程反演波阻抗剖面[J].地球物理学报.1994,37(1):101-107
[17]Xie GQ,A new iterative method for solving the coefficient inverse problem of the wave equation[J].Comm pure Appl Math,1986,XXXIX,307-332
[18]J.P.Boyd.Chebyshev and Fourier spectral methods [M].Courier Dover Publication,2001

