一种LFM信号参数估计的新方法

冯维婷, 张宝军

FENG Wei-ting, ZHANG Bao-jun

西安邮电大学 电子工程学院，陕西 西安 710121

School of Electronic and Engineering’ Xi’an University of Post and Telecommunications’ Xi’an 710121’China

1 引言

LFM 信号作为一种典型非平稳信号，在雷达、通信，声纳和地震勘测等领域有广泛地应用，关于 LFM信号参数估计有许多方法。最大似然(Maximum Likelihood)估计的方法[1-2]最早是1960年Kelly等人提出的，这种方法的性能最优，精度最高，但它在实际中需要进行二维极值搜索，计算量非常大。为了减小计算量，文献[3]采用二维牛顿迭代，但它需要有一个靠近真实值的初始值，否则将出现不收敛的情况。解线性调频(Dechirp)方法是工程中常采用的一种方法[4-5]，具有直观、信噪比门限低，加速度估计范围大的特点[6]。该方法需要有调频斜率变化范围的先验知识，对信号进行调频斜率补偿，再对补偿后的回波频谱进行谱峰搜索。基于Dechirp方法的参数估计需要在中心频率-调频斜率二维平面上进行峰值搜索，同样具有运算量大的特点。FrFT（Fractional Fourier Transform）作为一种新的时频分析方法[7-8]，是一种广义的傅里叶变换，其采用了线性调频基，特别适合于 LFM 信号的参数估计。但此方法进行参数估计时需要在分数阶傅里叶变换域构成的二维平面上进行峰值搜索，同样运算量很大。基于时频分析的一些其它方法[9-10]，也可用于LFM信号的参数估计，但以上这些方法都存在运算量大的问题。

为减少计算复杂度、提高运算实时性，Peleg等提出了离散多项式相位变换法[11-12]，该方法通过瞬时相关函数的方法，把对中心频率和调频斜率的二维搜索转变为两次一维搜索，但中心频率参数估计值受到误差传递效应影响，且调频斜率估计范围较小。

针对以上问题，本文提出了一种不同于以上方法的LFM信号参数估计新方法。基于降维思想，首先对信号进行数学变换，得到仅含多普勒中心频率的复正弦信号，通过FFT并用chirp-z变换进行频谱细化得到精确的多普勒中心频率估计值；然后根据先验知识在调频斜率的取值范围内，对回波进行调频斜率补偿；最后对补偿后的信号仅在中心频率估计值处进行单值非整数点DFT运算，从而得到一维调频斜率变化平面，通过搜索峰值获得信号调频斜率估计值。相比于二维峰值搜索算法，运算复杂度大大地降低，更利于实时处理。对比于离散多项式相位变换法，新方法的调频斜率估计范围不受限制，对中心频率的估计不受误差传递效应影响。仿真实验验证了算法的有效性。

2 中心频率的估计方法

混有噪声的LFM信号模型为x(t)=s(t)+w(t)，LFM信号定义为

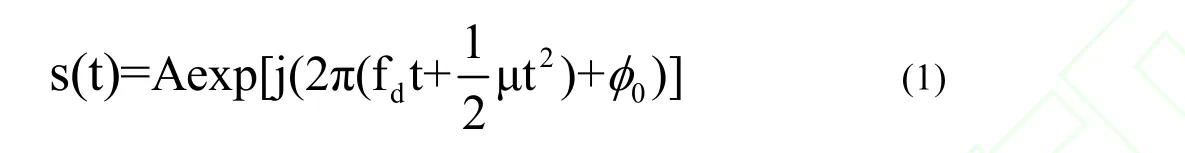
首先考虑fd的参数估计。受采样时间点对称的启发，定义x1(t)=x(t)x*(-t)。其中x*(-t)是对x(t)先取反转得x(-t)，再对x(-t)取共轭得到的。x1(t)可表示为

其中，w1(t)是x1(t)的噪声分量。由(2)式可见，x1(t)是一个混有噪声的单一频率复正弦信号。在没有噪声情况下，将x1(t)离散化为N点的序列x1(n)，其离散时间傅里叶变换用Yx1(ω)表示，见下式。

此时，x1(n)幅度频谱的最大值对应于2· fd频率位置处。式(4)可以利用FFT快速算法实现，但频谱离散化造成的误差较大。根据信号处理理论，信号的FFT变换可以获得其离散化的全局谱，Chirp-Z变换可获得全局谱中感兴趣的某段频谱的精细结构。本文利用Chirp-Z变换进行频谱细化，减小参数估计误差。频率为ω0的N点复正弦序列，在频域上表现为最大值在位置处的一个辛格函数。故要估计就是在频域上搜索其最大幅值，最大幅值处对应着的估计值。以复正弦序列估计频率为例，阐述细化频谱具体步骤。

1）对正弦序列进行N点的 FFT得离散为N点的全局频谱F(k)，k0是幅度最大值处对应的离散频率索引值；

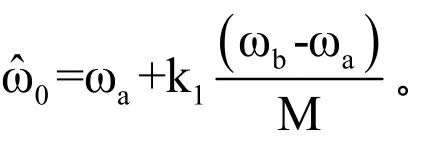
Chirp-Z变换有快速算法，可借助FFT实现[13]。经过Chirp-Z变换后，范围内的频谱频率分辨率变为∆ω=2πNM，比直接FFT的频率分辨率提高了M倍，可获得信号频率高精度的估计值。对x1(n)采用 Chirp-Z变换后，中心频率估计值的表达式为其中，f与f是包含谱峰值频ab率点的频率起点和终点，k1为Chirp-Z变换的谱峰值对应的离散频率索引值。

3 调频斜率的估计方法

在得到信号fd的估计值后，接下来考虑µ的估计。根据信号处理理论，对于时域有限长的LFM信号，其频谱由于调频斜率项的存在，是将其幅度频谱中对应于中心频率处的辛格函数展宽，且展宽的程度取决于调频斜率值。图1是LFM信号的幅度频谱。其中线性调频信号参数fd=900 Hz，取调频斜率分别为µ=0、µ=166.5 Hz/s进行对比。由图可见，调频斜率等于零的信号频谱，中心频率处对应峰值，能量集中于中心频率处；µ=166.5 Hz/s的信号频谱，频谱值明显下降，能量被分散在以中心频率为中心的带宽内。所以，对LFM信号在中心频率处进行解线性调频处理，在调频斜率的取值范围内对LFM信号进行补偿，即解除LFM信号的二次相位项调制，降为单一频率信号，则由于对应调频斜率µ处信号被完全补偿，频谱呈现尖峰，如图2所示。图中频谱最大幅值处与要估计的值对应。

图1 LFM信号的幅度频谱图

图2 处对应的调频斜率变化曲线

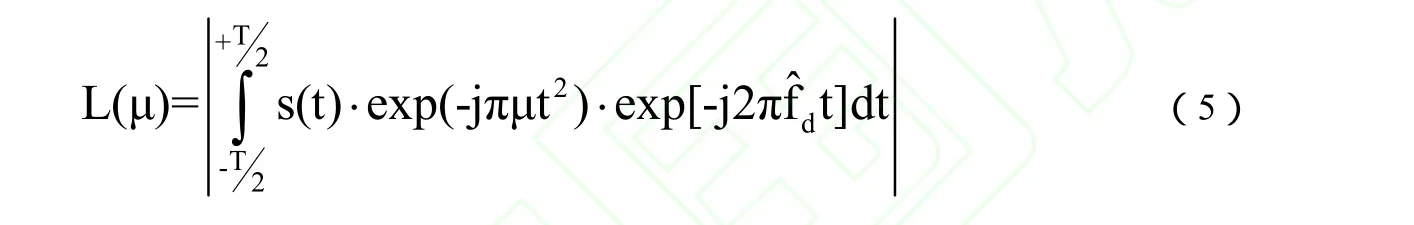
上式中，由于预先不知道调频斜率µ的值，需要根据先验知识，在一定范围内取值：µ∈[µstart,µend]。

对离散LFM序列进行补偿，获取调频斜率估计值的具体步骤如下：

1）在调频斜率µ∈[µstart,µend]的取值范围内，对LFM序列进行补偿。首先构造信号 exp(-jπµbt2)与 LFM序列x(n)相乘就是调频斜率补偿后的信号。式中第一次补偿时取i=0。Δµ为步长，需结合参数估计精度与运算量的实际要求综合考虑确定。

3）用[µstart,µend]内的第二个值µb=µstart+i·Δµ，（i=1），补偿离散序列x(n)，重复以上步骤，直到µb=µend结束，最后得到序列。搜索该序列最大值，最大值处对应的坐标就是估计值。

综上所述，本文提出的新方法，通过构造信号x1(t)，把线性调频信号的多普勒中心频率对应到一个单一频率的复正弦信号，搜索其FFT的峰值并结合频谱细化处理就可得到中心频率高精度的估计值。接着，对原信号进行调频斜率补偿，再对补偿后信号进行处的单值DFT，第二次搜索峰值得到调频斜率的估计值。需要说明的是，与fd估计不同的是，µ的估计精度不受数据离散化影响，而是鉴于实际应用的条件，取决于人为设定的Δµ值大小。故当Δµ值越小时，估计精度越高，但同时运算量越大。

4 计算复杂度分析

假设LFM信号离散化后的数据长度为N，调频斜率搜索次数为L。从以上分析可知，本文方法的计算量主要是：为了得到估计值的一次N点FFT和M点的Chirp-Z运算，为了得到的L次单值DFT运算。一次FFT的计算复杂度为O(NlgN)、一次Chirp-Z的为O((M+N-1)lg(M+N-1))[14]，L次单值DFT运算的为O(LN)，总计算复杂度为O[NlgN+(M+N-1)lg(M+N-1)+LN]。

与其它各种方法的计算复杂度对比：基于二维峰值搜索的 FrFT方法，当采用分解型快速算法时，可将离散FrFT分解为信号的卷积形式用FFT实现。当FrFT域扫描点数为L时，其计算复杂度为O(LNlogN)[15]；而基于二维峰值搜索的Dechirp方法，若调频斜率搜索次数也为L，其计算复杂度与FrFT方法相当。基于降维处理的离散多项式相位变换法，是对两次FFT结果的一维搜索，算法复杂度为O(2NlgN)。通过对比可见，对于固定的Chirp-Z变换点数M，当采样点数N和搜索次数L越大时，本文新方法的运算量远小于二维搜索算法的运算量，而接近于离散多项式相位变换法的运算量。当M=256，N=4096，L=1000时，采用本文方法的运算量为4197743，采用基于二维峰值搜索方法的运算量为49152000。由此可以看出，基于二维峰值搜索方法的运算量是本文方法的运算量的11.7倍。

5 计算机仿真分析

仿真实验：LFM信号参数设定为：幅度A=1，中心频率fd=899.5 Hz，调频斜率µ=166.35 Hz/s，采样点数N=2049，采样频率Fs=2049Hz。其中µ的搜索范围116 Hz/s～216 Hz/s，搜索步长为0.1 Hz/s，搜索次数L=1001；仿真中Chirp-Z变换点数M=256。表格1是本文方法与基于二维峰值搜索的Dechirp法运行时间的比较。仿真中信号模型未加入噪声，仿真环境为：Duo CPU E6550@2.33GHz ，4GB内存，Windows XP操作系统，MATLAB2008b。由表1可以看出，本文方法明显减少了程序运行时间。

表1 本文方法与Dechirp法运行时间的比较

图3所示为新方法与Dechirp方法、离散多项式相位变换法得到的参数估计值均方误差和CRLB下限的对比曲线。仿真结果显示，本文方法的参数检测信噪比门限为-8dB。

图3(a) 中心频率估计值均方误差曲线

图3(b) 调频斜率估计值均方误差曲线

图3(a)中，离散多项式相位变换法的参数估计是从µ开始的，由于误差传递影响，fd具有较差的估计性能。Dechirp方法的信噪比门限高，但中心频率估计性能曲线随信噪比的增加而性能未能提升，这是由于解线性调频处理后，中心频率估计性能受到FFT固有频率分辨率的制约。新方法的参数估计是从fd开始，其估计性能不受µ估计值的影响，同时还利用Chirp-z变换细化了频谱，提高了频率分辨率，因此能获得较好的估计性能。图3(b)中，离散多项式相位变换法对µ的估计性能也受限于FFT的频率分辨率。Dechirp方法对µ的估计精度取决于搜索步长Δµ，而在相同的Δµ条件下，新方法比Dechirp方法的性能曲线更接近CRLB下限。这是因为本文方法是从估计fd开始，fd估计值越精确，对应的µ估计值误差越小。

6 结语

本文提出了 LFM 信号参数估计的新方法。利用观测信号先构造新函数得到中心频率估计值；然后在调频斜率取值范围内对原信号进行补偿，对补偿后的信号在对应中心频率估计值处基于单值DFT运算、搜索峰值得调频斜率估计值。仿真结果表明，新方法对参数具有较好的估计效果，且计算复杂度低于二维峰值搜索方法、接近于离散多项式相位变换法，因此更利于快速高精度的参数测量。

[1]Kelly E J.The radar measurement of range, velocity and acceleration [J].IEEE Trans on Military Electronics,1961, MIL-5:51-57.

[2]Li Y, Fu H, Pooi Y K.Improved, approximate, time-domain ML estimators of chirp signal parameters and their perform analysis [J].IEEE Trans.on Signal Processing , 2009, 57(4) :1260- 1272.

[3]Abatzoglou T J.Fast maximum likelihood joint estimation of frequency and frequency rate [J].IEEE Trans on AES, 1986, 22(6):708-715.

[4]李文臣，王雪松，刘佳琪，等.线性调频参数估计方法的数学统一[J].信号处理, 2009,25(8) :1292-1297.

[5]张贤达，保铮.非平稳信号分析与处理[M].北京：国防工业出版社，2001,158-164.

[6]苏军海, 吕孝雷，邢孟道.窄带雷达高速多目标检测及其运动参数估计[ J].系统工程与电子技术, 2009,31(7):1539-1543.

[7]齐林，陶然，周思永，等.基于分数阶Fourier 变换的多分量LFM信号的检测和参数估计[J ].中国科学(E),2003,33(8):749-759.

[8]屈海涛, 齐林, 穆晓敏, 等.基于FRFT的多分量LFM信号DOA估计[J].计算机工程与应用, 2007, 43(35):65-67.

[9]Barbarossa S.Analysis of multi component LFM signals by a combined Wigner-Hough transform [J].IEEE Trans on Signal Processing, 1995, 43(6):1511-1515.

[10]Wood J C, Barry D T.Linear signal synthesis using the Radon-Wigner transform[ J].IEEE Trans on Signal Processing, 1995, 43(6):1511-1515.

[11]Peleg S , Porate B.Estimation and classification of polynominal-phase signals[ J].IEEE Trans on Information Theory, 1991, 37(2):422-430.

[12]Peleg S , Porate B.Linear FM signal parameters estimation from discrete time observations[ J].IEEE Trans on AES, 1991, 27(4):607-616.

[13]程佩青.数字信号处理教程[M].北京：清华大学出版社，2001,172-177.

[14]陈祝明，丁义元，向敬成.采用 Chrip-Z变换提高 LFMCW 雷达的测距离精度[J].信号处理,2002,18(2):110-112.

[15]Ozaktas H M, Arikanet O, Kutay M A,Bozdagl G.Digital computation of the fractional Fourier transform [J].IEEE Trans on Signal Processing, 1996, 44(9):2141-2150.