定量变量的分级方法对logistic模型影响的研究*

周凌峰 安胜利

logistic回归分析是用于筛选影响因素及建立预测模型的最常用的方法之一，它的综合预报效果具有很好的稳健性和非模糊性[1-2]。在logistic回归分析中，常会用到三种自变量类型：定量变量、等级变量及分类变量，为使得OR值具有更明确的临床意义或便于预测模型的实际应用，研究者[3-5]常将有统计学意义的定量变量转化为两个或两个以上等级，并赋予相应的分数。但目前等级划分方法大多是由研究者主观决定，若分界点选择不当，其模型预测效果便会受到影响，甚至会影响到研究结论的正确性。本研究拟在计算机上以常用的非条件二分类logistic回归分析为例进行模拟研究，在不同的参数条件下，对有统计学意义的自变量进行不同数量、不同方式的等级划分，建立预测模型，考察其预测效果的变化规律，并对所得结论以实例进行考核，以期发现各种参数条件下合理的等级划分方法。为建立更准确、实用的logistic预测模型提供可靠的变量转化依据。

方 法

为了便于解释，本研究将模拟数据简化设计为仅有一个自变量X(连续变量)及一个因变量Y(0-1变量)，然后观测各种转换方法对预测模型的影响规律，进而延伸说明多个自变量情况下该指标的变化状况。

1.自变量

利用R语言，模拟产生单个自变量，考虑三种分布状况，即标准正态分布、正偏态分布、负偏态分布。标准正态分布使用rnorm( )语句直接生成。正(负)偏态则采取以下方法产生。以正偏态为例，生成1000例标准正态分布数据，并截掉大于0.8的部分，同时再生成1000例0至5.5服从均匀分布的数据，合并二者后，从中选取1500例，最后得到近似正偏态的数据。负偏态自变量采取类似方法。

2.因变量

为了保证原始数据中自变量与因变量经logistic回归分析具有一定的联系，因变量可利用自变量通过公式产生；鉴于因变量0、1的分布在实际数据中存在不同，我们通过调整OR值来改变Y的分布。方法如下：

利用logistic回归模型计算阳性事件发生概率P：

(1)

式中e为随机误差，服从标准正态分布。

假定β0为任意已知常数，如0.2，取βm为log(OR)，并取多种OR值情况(如OR=1.5～5,以0.5为间隔)。当确定某OR值后，便可通过上式计算相应的阳性事件发生概率P，对应的因变量Y则由0-1二项分布函数计算得到。

3.确定样本含量

对上述产生的数据逐步增加样本含量，并观察自变量转换后，其与因变量的关系变化，当这种关系稳定时所对应的样本含量即为所需模拟的样本含量大小。经测试，样本量为1500时满足上述要求。

4.自变量分级方法

共考虑三种分级数，即二级、三级、四级分类。

(1)二级分类

均数分级：以均数为分割点分为两级；中位数分级：以中位数为分割点分为两级；ROC分级：对自变量与因变量做ROC曲线，取约登指数最大的自变量值为分割点。分别赋为0、1。

(2)三级分类

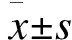
(3)四级分类

百分位四等分：将自变量从小到大排序，并依据总的样本量平均分为四级，各级观察单位数约占总样本量的25%；极差四等分分级：自变量最大值减最小值所得区间平均分为四份，分别赋为0、1、2、3。

5.评价指标

从现行的一些研究来看，学者们[6-9]较为关注两个方面，一方面是分级后的自变量对因变量的预测准确程度；另一方面，分级后变量在回归中的拟合效果。对于前者，人们普遍采用ROC曲线下面积AUC[10]来衡量其优劣程度，本研究亦采用AUC作为其中一种评价指标。在第二方面，本研究拟采用AIC信息量[11]。

在各种参数条件下(OR=1.5～5,以0.5为间隔)，对模拟数据(分别对不分级、各分级情形)计算AUC，同时再进行logistic回归计算AIC信息量，重复模拟1000次，并计算上述两指标的平均值及标准差。

6.模拟次数确定

不同分布、不同OR值下，当AUC、AIC均值达到稳定时所对应的模拟次数即为所需模拟的总次数。经过测试，本研究各种情况下模拟次数取1000次即可达到稳定。

结 果

正态和部分正偏态分布模拟结果见图1-图5。

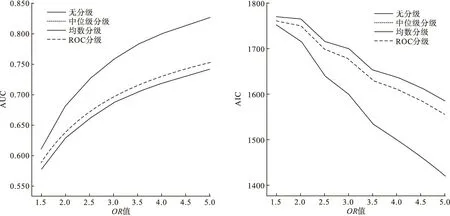
图1 正态分布分二级

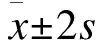
1.二级分级

正态分布下均数与中位数分级结果基本没有区别(理论上也应如此)。分级首选为ROC分级，其次为均数或中位数分级。

偏态分布时，首选ROC分级，其余方法AUC和AIC两指标无法同时最优，若以AIC为首选指标，则最优为均数分级，若以AUC为首选指标则最优为中位数分级。

2.三级分级

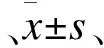
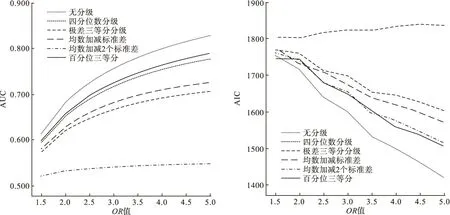
图2 正态分布分三级

偏态时，均数±标准差不宜作为统计描述指标，因此不做模拟，从优到劣的分级方法顺序为百分位三等分、四分位数分级、极差三等分分级。

3.四级分级

正态分布或偏态分布下，方法优先顺序均为百分位数四等分分级、极差四等分分级，其中偏态分布下，OR值<3时，AIC信息量曲线略有交叉，OR>3后百分位数四等分分级AIC略优于极差四等分，但二者区别不大。

实例考核

1.实例背景

某研究在各个时间点均获得57名病人的各指标结果，如neu,wbc,crp等，并以记录病人是否发生了感染(1-发生感染，0-未发生感染)，目的是用特定时间的指标建立诊断、预测感染的模型。现假设需要对其中的第9个时间点的某定量指标(neu9)进行分级，将其转换为等级变量来建立预测感染模型。

2.实例分级验证

首先，确定该定量变量(neu9)的分布，经Kolmogorov-Smirnov以及Shapiro-Wilk正态性检验，P值均大于0.10，可以近似看作正态分布。经logistic回归分析，有统计学意义，并计算出该变量OR值为1.1，假定欲将neu9分别分为二级、三级、四级，所得结果如表1。

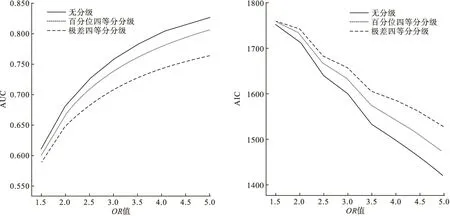
图3 正态分布分四级

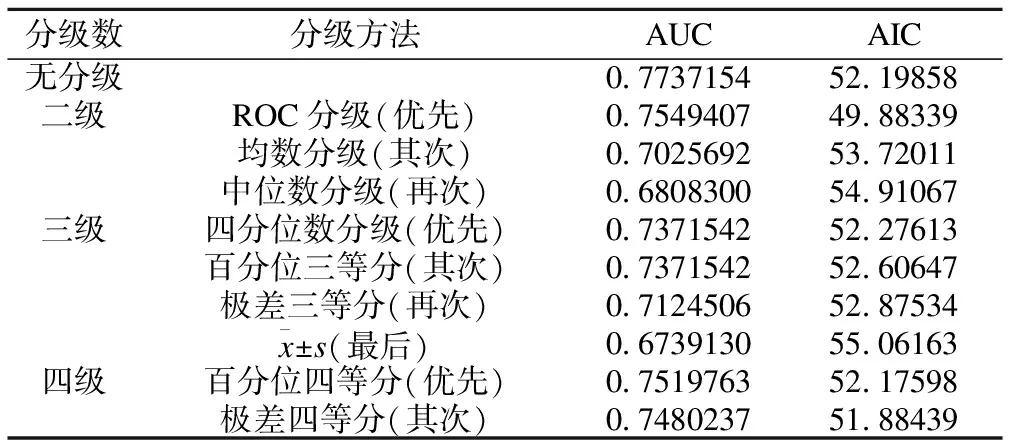
表1 实例考核结果

该定量变量OR<1.5，对比前述模拟结果，由表1可知，实例数据所得结论基本符合模拟结果给出的预期结论。

由此，综合以上结论分析，我们可以给出OR为1.5～5内的一个简明的分级建议，见表2。

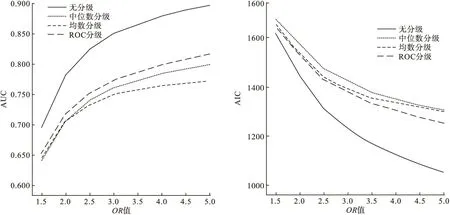
图4 正偏态分布二级

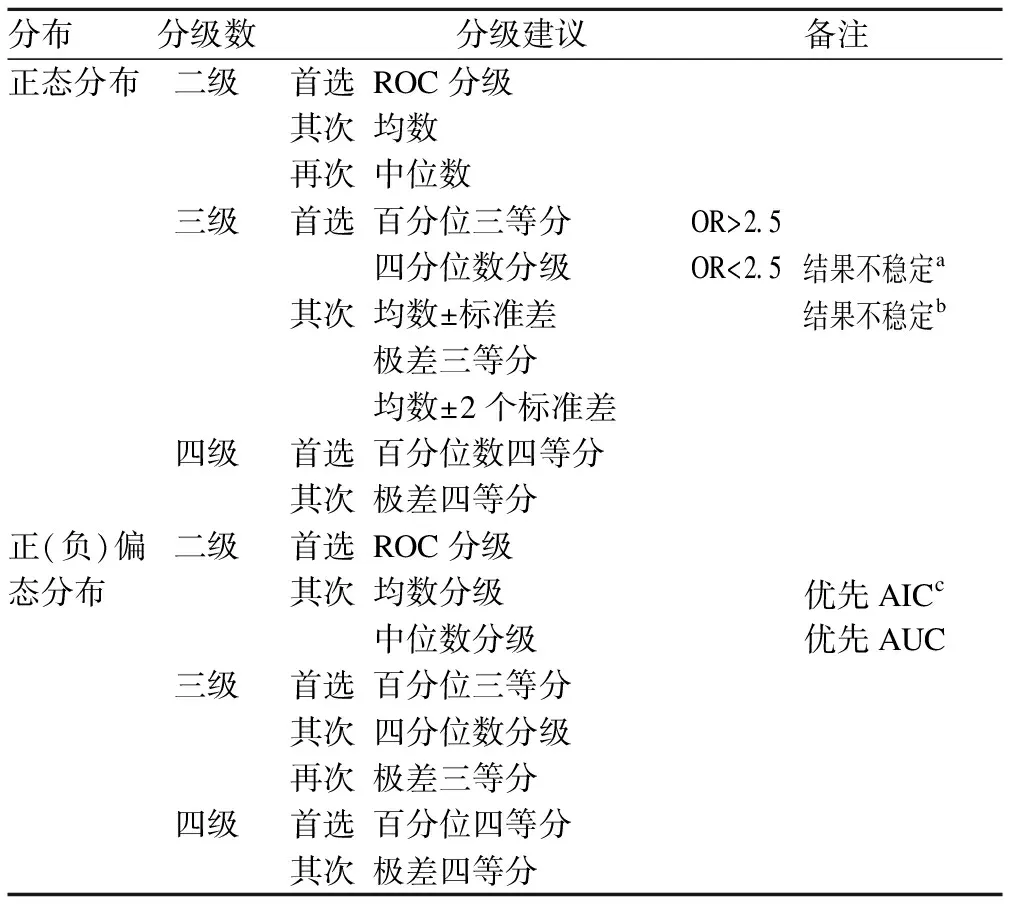
表2 三种分布分级建议

其他数据分布若与上述特定分布存在较大偏差，则最优分级方法可能会与上述分级建议不一致。建议通过比较不同分级方法下的ROC曲线下面积、AIC信息量两指标，择优选择。

改进方向

目前还有一些其他学者提出的分级方法未能在本研究中进行演示，拟在今后的研究中，继续拓展分级方法，给出更多的分级参考。另外，由于偏态分布模拟没有特定的参数标准，实际的偏态分布形式多样。经本研究的验证，不同偏态分布数据可能得到不同最优分级方法，因此对于特定偏态分布本研究的分级建议参考价值有限。本研究在数据模拟中，OR值取值范围为常见的1.5～5(以0.5为间隔)，如果继续扩大OR值的取值范围，AUC和AIC结果会否出现其他结论？其对分级方法的选择又有何影响？这将在以后的研究中继续探讨。

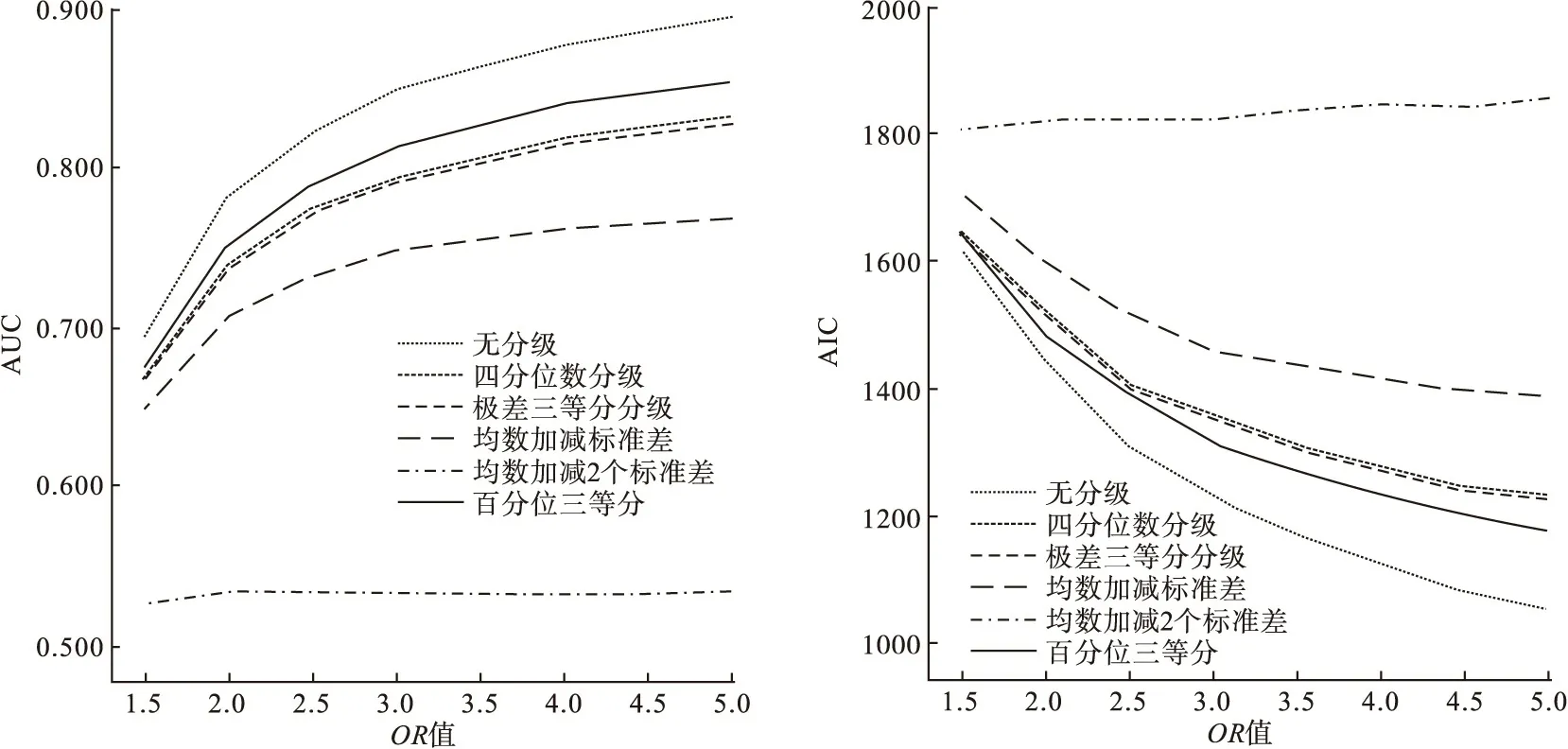
图5 正偏态分布三级

参 考 文 献

1.钟晓妮,周燕荣.女性乳腺癌预报模型研究.数理医药学杂志,2002,15(1):4-6.

2.Steyerberg EW,Eijkemans MJ,Harrell FE Jr.Prognostic modeling with logistic regression analysis:in search of a sensible strategy in small data sets.Medical Decision Making,2001,21 (1):45-56.

3.万伟.影响老年高血压患者血压控制率因素的Logistic回归分析.高血压杂志,2001,9(1):74-75.

4.陈晖,王小波,张丽萍，等.中老年人牙列缺损危险因素的Logistic回归分析.山东医药,2010,50(48):48-49.

5.Subherwal S,Richard GB,Anita YC,et al.Baseline Risk of Major Bleeding in Non-ST-Segment-Elevation Myocardial Infarction.Circulation,2009,119:1843-1845.

6.刘宝利,杨宝友,郑桂敏，等.logistic回归和ROC曲线综合评价检测四种尿蛋白排泄对早期肾小球疾病的诊断价值.中国中西医结合肾病杂志,2011,12(8):695-697.

7.Kheterpal S,Kevin KT，Heung M,et al.Development and Validation of an Acute Kidney Injury Risk Index for Patients Undergoing General Surgery.Anesthesiology,2009,110:505-15.

8.Kim MY,Jang HR,Wooseong Huh.Incidence,Risk Factors,and Prediction of Acute Kidney Injury After Off-Pump Coronary Artery Bypass Grafting.Renal Failure，2011,33(3):316-322.

9.Palomba H,de Castro I,Neto ALC,et al.Acute kidney injury prediction following elective cardiac surgery:AKICS Score.Kidney International，2007 (72):624-631.

10.李康.连续变量诊断试验数据的ROC分析.中国卫生统计,2007,14(1):1-4.

11.王济川,郭志刚.Logistic回归模型——方法与应用.北京:高等教育出版社.2001.