采用多自由度转子模型的电磁轴承支承特性测试方法

蒋科坚， 祝长生， 乔晓利， 陈亮亮

(1．浙江理工大学信息学院，浙江 杭州 310018； 2．浙江大学电气工程学院，浙江 杭州 310027)

引 言

主动电磁轴承(active magnetic bearing, AMB,以下简称电磁轴承)是一种新型的转子支承技术。它采用主动电磁力把转子悬浮在期望位置，实现与传统机械轴承相类似的转子支承能力。相比较，电磁轴承不仅可以无接触地支承转子，避免传统机械轴承出现的摩擦发热、润滑、疲劳等问题，满足转子高速旋转的要求，而且还可以通过控制策略对轴承的动力学特性进行实时调节，实现对转子系统振动的主动控制。

在传统的转子动力学研究中，通常采用轴承的刚度阻尼模型来描述轴承的支承特性。在电磁轴承研究领域，为了描述电磁轴承的支承特性也沿袭了轴承的刚度阻尼概念，称之为等效刚度和等效阻尼。虽然描述电磁轴承的支承特性有多种方式，但等效刚度和阻尼是最广泛采用的表示形式。然而，电磁轴承的支承特性不仅与轴承的结构尺寸有关，还决定于其控制器所采用的控制策略和参数，因此从理论上对电磁轴承等效刚度和阻尼参数的分析和确定十分困难。已有的研究表明，如果要理论计算电磁轴承的支承特性(即轴承的刚度和阻尼)，必须已知控制系统的传递函数。然而，目前很多实际电磁轴承控制系统的输入输出关系不能够简单的归结出一个传递函数表达式。再者，当融入了数字信号处理和振动控制算法的控制策略更难以用传递函数的形式来表示。这种无法得出传递函数的情况在电磁轴承控制中是普遍存在的，导致了理论计算电磁轴承支承特性的困难。因此，采用近似估算，并通过实验测量验证估算方法的正确性，显得尤为重要。

目前对电磁轴承刚度阻尼参数的测量和推导，以及基于等效刚度和等效阻尼的电磁轴承转子动力学分析已有大量研究。Tsai等应用小波变换识别电磁轴承的等效刚度和阻尼[1]，分析了等效刚度阻尼的非线性阶次，并发现电磁轴承等效阻尼可能为负值的现象，意味着在某些位移和转速下，控制是不稳定的。Lim等采用激励的方法[2]，识别了PID控制策略下电磁轴承的等效刚度和阻尼参数，分析其变化规律。Kim等提出了基于自适应滤波器的方法[3]，通过最小均方误差自适应收敛得到电磁轴承的电流刚度系数和位移刚度系数。Mehmet等和Lim等提出多频激励方法进行电磁轴承等效刚度的识别[4，5]，采用施罗德谐相序列有效避免了因激励信号峰值叠加引起的激励饱和问题。Bauomy分析了电磁轴承转子系统在周期时变刚度条件下的非线性响应行为[6]，并用4阶Runge-Kutta法分析了系统在同步振动和子谐波共振下的稳定性。Sayyad研究了用可变刚度的电磁减震器控制悬臂梁的振动[7]，其工作原理与单自由度方向上电磁轴承通过调节刚度抑制转子振动是相同的。在国内，对电磁轴承支承特性也做了大量研究。虞烈较早地对电磁轴承-转子系统支承特性展开了系统的理论研究[8]。胡业发等研究了由电磁轴承结构引起的等效刚度和阻尼交叉现象[9]。赵雷等研究了定转子气隙和定子静态偏置磁通密度与等效刚度的关系[10]，认为其线性范围决定轴承的最优性能，以此为依据得到最优等效刚度对应的轴承结构参数。吴华春等对滤波、滞后、衰减等因素对电磁轴承等效刚度的影响进行了理论分析[11]。杨作兴等提出了单自由度复刚度的测试方法[12]。赵晶晶等提出基于激振识别的单自由度等效刚度和阻尼的测量方法[13]。

1 问题的提出

首先需要讨论的是，由于电磁轴承控制策略设计的复杂多样性，用传统的刚度和阻尼概念来表示电磁轴承的支承特性，是否存在描述的局限性。因为只有在等效刚度和等效阻尼的概念描述适用的前提下，再来讨论如何分析或测试电磁轴承的等效刚度和阻尼才显得有意义。

其次是如何对一个实际电磁轴承的等效刚度和阻尼参数进行实验测试，以使得理论推导与实验测试相互验证。目前已有的电磁轴承等效刚度和阻尼测试方法大多都是基于单自由度模型的，不能适用于实际多自由度转子系统的测试，甚至无法实际操作。譬如，若要对多自由度的电磁轴承-转子系统支承特性进行测试，许多文献采用的方法是将转子一端搁在备用轴承上作为支点，另一端用电磁轴承悬浮并施加激励测试。此时转子系统近似成杠杆结构，可等效为一个单自由度的质量-弹簧-阻尼系统。最后，基于这个近似的单自由度模型，实现等效刚度和阻尼的振动参数识别。

这种单自由度电磁轴承等效刚度和阻尼的测试方法显然是存在问题的。对于水平放置的转子结构，虽然可以利用转子重量使转子一端搁在备用轴承上，可近似为支点。但是，因为转子在各自由度上的运动是耦合的，这一端电磁轴承的激励会影响转子另一端与备用轴承的稳定接触。一旦接触不稳定，就会破坏这种近似杠杆结构的等效条件。另一方面，如果是直立的转子结构，这种单端悬浮激励的杠杆等效方法根本无法实现，无法实际操作。

因此，针对上述问题，本文首先分析了多自由度刚性转子系统在电磁轴承支承条件与传统机械轴承支承的差异和联系，理论阐述了采用等效刚度和等效阻尼表示电磁轴承支承特性的适用范围和描述局限性。然后，在适用的前提下，提出了一种基于多自由度转子模型的，在转子正常悬浮条件下能够对电磁轴承径向支承的所有等效刚度和阻尼参数进行同时测量的方法。该方法对于两个电磁轴承支承的刚性转子系统的支承特性测试具有普遍的适用性和可操作性，以满足实际复杂转子动力特性测试的需要。

2 单自由度电磁轴承支承的等效刚度和等效阻尼

对于单自由度的电磁轴承支承，其等效刚度和阻尼的概念是简单明确的，即把电磁轴承-转子系统在某一方向的支承特性等效为传统的单自由度质量-弹簧-阻尼系统。利用与传统机械振动系统刚度和阻尼的对比，得到电磁轴承的等效刚度和阻尼参数。

单自由度质量-弹簧-阻尼系统在时域的运动方程和拉氏变换后的频率特性方程分别为

⟹

(1)

式中F为系统受到的外激励力，X为位移，m为质量，k和d分别表示系统的刚度和阻尼。

一个电磁轴承支承的单自由度系统，在线性电磁力条件下其运动方程为

(2)

式中fAMB为电磁轴承的电磁力，I为控制电流，kx和ki分别为电磁轴承的位移刚度系数和电流刚度系数。

对式(2)进行拉氏变换，并且把控制电流与位移关系表示为传递函数的形式，即I(s)=G(s)X(s)，其中G(s)为电磁轴承控制系统的传递函数，可得到频率特性方程为

⟹

(3)

比较式(1)和式(3)，容易得到单自由度电磁轴承系统的等效刚度k和等效阻尼d表达式

(4)

式中 Re{ }和lm{ }分别表示复数的实部和虚部运算。可见，要理论上计算电磁轴承的等效刚度和阻尼必须要知道电磁轴承控制系统的传递函数G(jω)(以下简写为G)。

另一方面，根据式(1)的频率特性方程关系，也可通过激振实验，测量激励和响应之间的幅值和相角关系，求得k和d的值。大多数基于单自由度模型识别电磁轴承的等效刚度和阻尼的测量方法就是基于这个原理。

3 多自由度电磁轴承-转子系统的径向等效刚度和等效阻尼

目前文献对复杂结构刚度阻尼的概念和定义存在一些差异。为了清楚起见，本文所述的电磁轴承转子径向支承的等效刚度和等效阻尼是指，把电磁轴承对转子的径向支承等效为如图1所示的弹簧-阻尼支承结构。将电磁轴承的电磁力等效为弹簧力和阻尼力，电磁力方向如图分别为xa,xb,ya,yb，且4个方向的弹簧-阻尼支承互相独立，即每个方向上弹簧力和阻尼力只是自己方向上的位移和速度的函数。如此等效后，4个方向支承所体现的刚度和阻尼，共8个参数(虽然由于位移传感器安装尺寸的限制，使得位移检测与电磁线圈不在同一位置。为了简化模型，本文近似认为电磁轴承对转子的电磁力作用点与位移检测点在同一位置)。

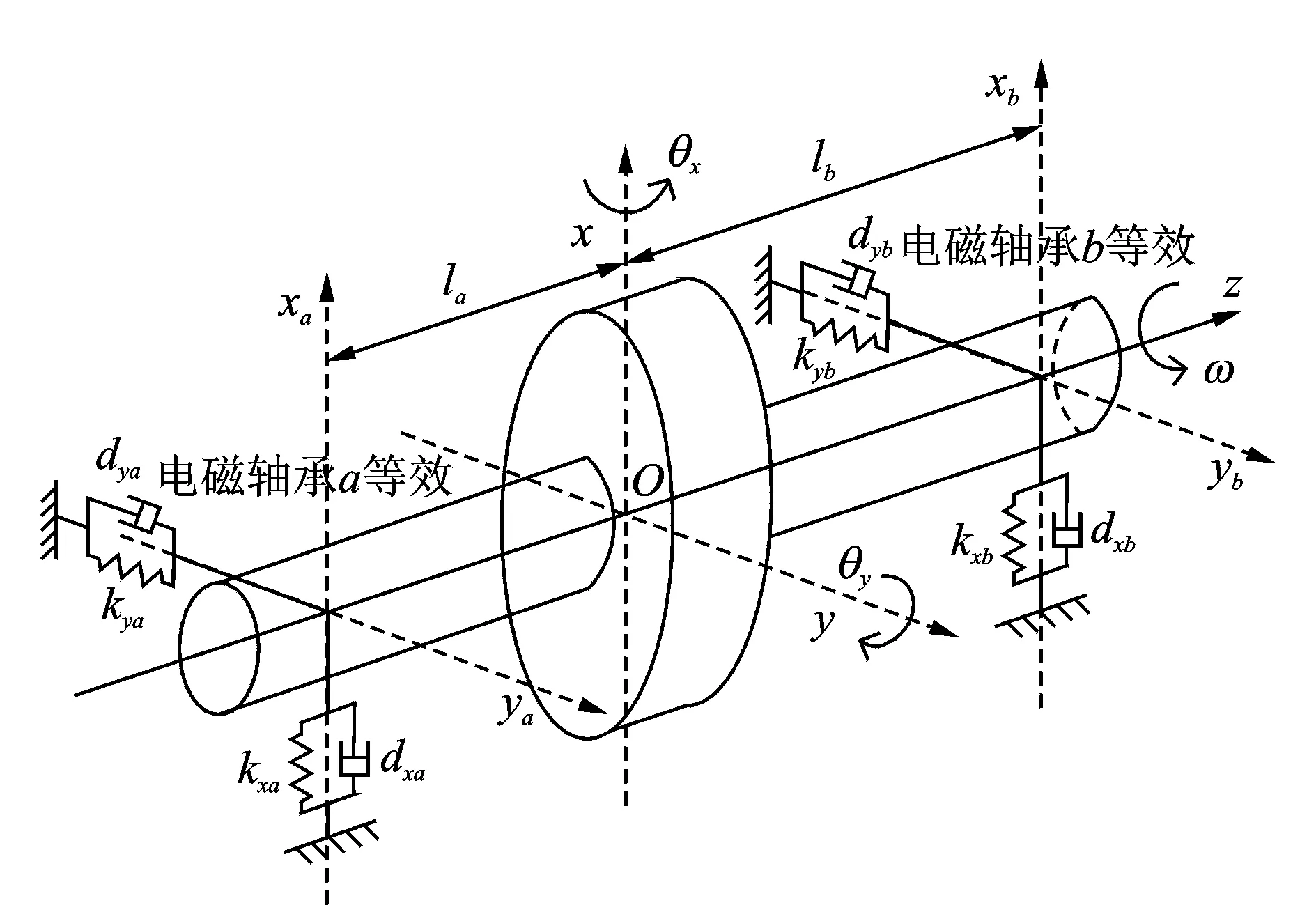
图1 电磁轴承-刚性转子系统的等效模型

根据转子动力学理论，刚性转子在空间的运动姿态可以用6个自由度来描述，分别为按空间3个互相垂直轴方向的平移(2个径向，1个轴向)和绕这3个轴的旋转。已有的研究表明，当转子处于静止或低速旋转时，其径向和轴向之间，以及两个互相垂直的径向平面之间的运动耦合都可以忽略。

对于图1所示的刚性转子系统，在静止或低速旋转条件下，需要获得径向电磁轴承电磁力与转子运动之间的关系。设O为转子系统的质心，z轴为转子旋转轴，两个径向电磁轴承的作用力位置与转子质心的距离分别为la和lb，两个径向电磁轴承间的距离为l=la+lb。设转子运动向量为[X,θy,Y,θx]T，其中X和Y为转子质心在x和y轴方向上的位移，θy为转子绕y轴在xz平面上的转角，θx为转子绕x轴在yz平面上的转角，均以图中所示箭头方向为正。另设[xa,xb,ya,yb]T为转子在两电磁轴承处的位移，则[xa,xb,ya,yb]T与[X,θy,Y,θx]T间的坐标转换关系为

(5)

设径向电磁轴承在各方向上的等效刚度和阻尼分别为kxa,kxb,kya,kyb及dxa,dxb,dya,dyb。为了更贴近实际情况，这里假设电磁轴承各方向上的等效刚度和阻尼参数都不同。

首先，以电磁轴承的等效刚度和阻尼的形式表示图1所示刚性转子系统的运动方程

(6)

式中m和J分别为转子的质量和赤道转动惯量，Fx和Fy分别为x和y方向的外激励力，Mx及My分别为Fx和Fy相对于转子质心的外力矩。

将式(5)代入(6)，并用矩阵表示为

(7)

对式(7)进行拉氏变换，得到的频率特性方程为

(8)

为简化公式书写，其中，ma=mω2la/l，mb=mω2lb/l，Jr=Jω2/l。

然后，以电磁轴承电磁力的形式，重新推导图1所示转子的运动方程。设径向电磁轴承各方向上的电流刚度系数和位移刚度系数分别为ki xa,ki xb,ki ya,ki yb及kx xa,kx xb,kx ya,kx yb，则在电磁力线性范围内，转子系统的运动方程可表示为

(9)

式中Ixa,Ixb,Iya,Iyb分别为径向电磁轴承在各方向上的控制电流。

同样，也将式(5)代入式(9)，整理为矩阵形式

①分散控制策略: 即在某方向上电磁力的控制电流只与该方向上的转子位移有关，可用对角形式的传递函数矩阵表示为

(11)

式中G为控制电流与转子位移间的传递函数关系，其下标表示控制电流和位移方向的对应关系。

对式(10)进行拉氏变换，代入式(11)整理后得

(12)

比较式(12)和式(8)，可以容易得出采用分散控制策略的电磁轴承-转子系统等效刚度和阻尼的表达式为：

kxa=kixaRe{Gxaxa}-kxxa;dxa=kixaIm{Gxaxa}/ω；

kxb=kixbRe{Gxbxb}-kxxb;dxb=kixbIm{Gxbxb}/ω；

kya=kiyaRe{Gyaya}-kxya;dya=kiyaIm{Gyaya}/ω；

kyb=kiybRe{Gybyb}-kxyb;dyb=kiybIm{Gybyb}/ω

(13)

可见，当采用分散控制策略时，转子的径向自由度支承特性可用如图1所示的各方向独立的刚度阻尼结构模型来描述，每个方向的等效刚度阻尼只与本方向的电流刚度系数和位移刚度系数有关。

②同一平面内的交叉控制: 即控制电流与x或y同一平面内的转子两侧位移都有关。在解决转子在同一平面内的机械运动解耦时，经常采用这类控制方法。传递函数矩阵表示如下

(14)

对式(10)进行拉氏变换，代入式(14)整理后得

=

(15)

比较式(15)和式(8)，也可以得出采用同一平面内交叉控制的等效刚度和阻尼的表达式为

(16)

可见，当采用同一平面内的电磁力交叉控制时，转子的径向自由度支承特性仍可用如图1所示的4个方向独立的刚度阻尼结构模型描述。每个方向的等效刚度阻尼参数包含了同平面互相交叉的两个电流刚度系数项，而位移刚度系数项不交叉。

③不同平面之间的交叉控制时，即控制策略中有x和y两平面之间的电磁力交叉控制。在考虑转子的陀螺效应解耦时，会采用这类控制方法，传递函数矩阵表示为

(17)

同样将式(17) 代入式(10)的拉氏变换，整理后与式(8)比较发现，等号左边矩阵的形式不一致，出现了xy平面之间的非零交叉项。这说明传统的刚度阻尼概念无法全面地表达电磁轴承在不同平面之间交叉刚度阻尼的概念。

虽然，在转子动力学中，对传统机械轴承已经有交叉刚度和交叉阻尼的概念，但这与电磁轴承的情况是有本质区别的。原因在于，电磁轴承等效刚度表达式中包含两项，如式(4)，位移刚度系数kx项(一些文献称之为被动刚度)和电流刚度系数ki项(一些文献称之为主动刚度)。传统机械轴承的交叉刚度只能近似于电磁轴承交叉刚度中的被动刚度部分的概念。对于电磁轴承的主动交叉刚度目前尚没有公认的统一的表示方法。目前，有些文献把同平面内和不同平面之间的交叉刚度统一起来表示；另一些文献直接用电磁力在模型中表示；还有一些文献把等效刚度和阻尼考虑为转子的基本悬浮环境，把振动控制，如陀螺交叉解耦、不平衡力控制等，作为附加电磁力处理。但上述都只是针对某一具体问题提出的表示方法，目前尚没有被普遍公认的统一方法或表示参数。

4 多自由度刚性转子系统支承特性测量方法

在电磁轴承-转子系统等效刚度和等效阻尼的测量中，只有上述控制策略的前两种情况，其测量才是有意义的。当采用不同平面之间的电磁力交叉控制，等效刚度和阻尼不能充分描述电磁轴承的支承特性，测量结果也是无意义的。本文所述测量方法只限用于前两种情况。

对于图1所示的径向电磁轴承-刚性转子系统，其系统等效模型的频域形式可用式(8)表示。为了叙述方便，令式中的

Axa=kxa+jωdxa，Axb=kxb+jωdxb，Aya=kya+jωdya，Ayb=kyb+jωdyb

(18)

代入式(8)后，可得

(19)

在式(19)中，激励信号和转子响应在激振测试中是已知量，而4个未知复数量Axa,Axb,Aya,Ayb是待测的。显然，式(19)是一个四元一次复数方程组。如果能通过激振实验得到4个不相关的复数方程，则从方程组(19)中可以解得与等效刚度和阻尼参数相关的4个复系数为

(20)

解出Axa,Axb,Aya,Ayb后，可根据式(18)得到等效刚度阻尼参数的测量结果为

(21)

理论上，两个电磁轴承任何组合形式的激励，都可测得响应数据，完成式(19)的方程组求解。为了简化测试和方便求解过程，本文采用在一个电磁轴承x和y方向的控制电流中分别叠加正弦和余弦激励信号的激励方法，形成矢量轨迹为圆形的激励力。在转子悬浮时，只要在一个电磁轴承叠加激励测量一次，便可得到4个方程，求解所有8个等效刚度阻尼参数。

另外，关于如何在有噪声的全频振动信号中，提取与激励频率对应的同频响应信号成分的方法，可参考文[15,16]或其他文献，因篇幅所限，本文不再重复叙述。

5 实验和分析

5.1 实验装置

实验装置为如图2所示的电磁轴承-立式刚性飞轮转子系统。转子径向由上下两个电磁轴承支承，轴向由一个永磁轴承支承。径向电磁轴承悬浮间隙为0.3 mm，辅助轴承间隙为0.2 mm。如图3是转子结构简图，转子的质量m=58.32 kg，赤道转动惯量J=1.878 kg·m2。以电磁轴承转子的中心作为电磁力作用点，质心位置按转子各分段的材料和尺寸算出，得到la=305 mm,lb=222 mm。两个电磁轴承的电流刚度系数，上电磁轴承为326.15 N/A，下电磁轴承为111.32 N/A。悬浮控制和测量是在d-SPACE DS1103实验平台上实现的。控制器采用4自由度的分散PID控制，增加了数字滤波器和近似微分环节以降低噪声干扰。转子悬浮控制采样频率为50 kHz，激励测试实验在10 kHz采样频率下进行。

图2 电磁轴承-刚性转子实验系统

图3 转子结构简图

为了大致掌握转子系统在1～200 Hz待测频率范围内的振动情况，事先测试了转子各自由度的振动幅频特性。图4和5分别为施加激励后上下电磁轴承处，所检测到的转子振动幅频特性图。由图中可知，在各个方向上，转子随频率变化的振动峰值集中出现在20 Hz和60 Hz频率段。其中在26 Hz和54 Hz处有2个较大的振动峰值，应为转子系统刚体振型的锥动和平动的2个模态频率。其他较小峰值是转子多个自由度之间的运动耦合引起的。由于转子各方向上的等效刚度和阻尼有一定差异，引起了各方向共振频率的差异，并且相互耦合影响。当激励频率超过100 Hz后，转子的振动幅值迅速减小。

图4 上电磁轴承处的转子振动幅频特性

图5 下电磁轴承处的转子振动幅频特性

5.2 实验结果和分析

首先，用上侧电磁轴承施加激励进行测试，分别在x和y方向施加正弦和余弦激励电流，形成圆形矢量轨迹的激励力，激励力幅值为20.83 N。激励力幅值选取原则是能够保证在整个待测频率范围内，施加激励不能破坏转子的悬浮稳定性。即使在临界频率附近振动较大，也至少能维持悬浮状态。通过上侧电磁轴承施加激励测试，得到了上电磁轴承x及y方向和下电磁轴承x及y方向上的等效刚度和等效阻尼的测试结果分别如图6和7所示(等效阻尼由于彼此接近，未标明方向)。

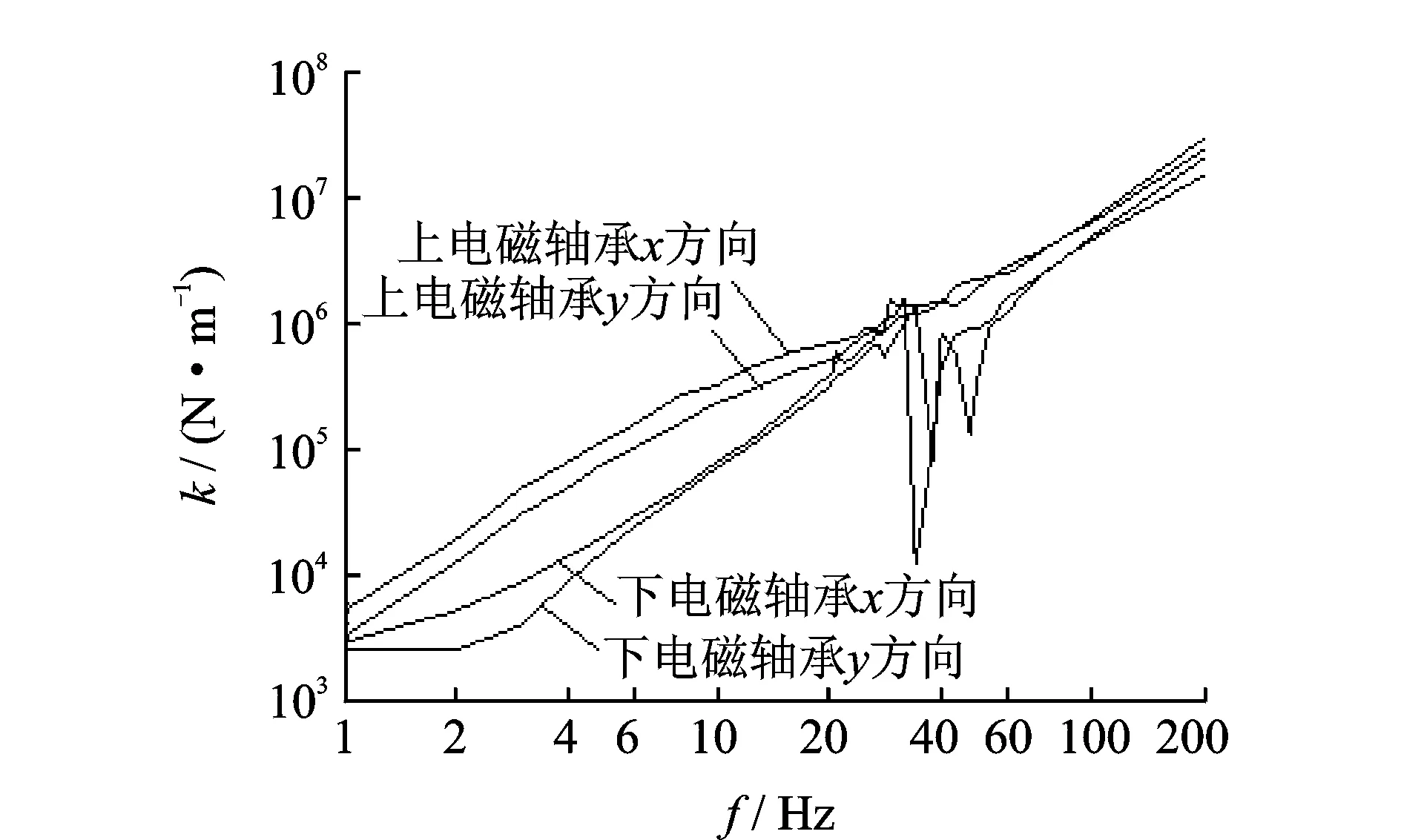
图6 上电磁轴承激励得到的4个方向等效刚度测试结果

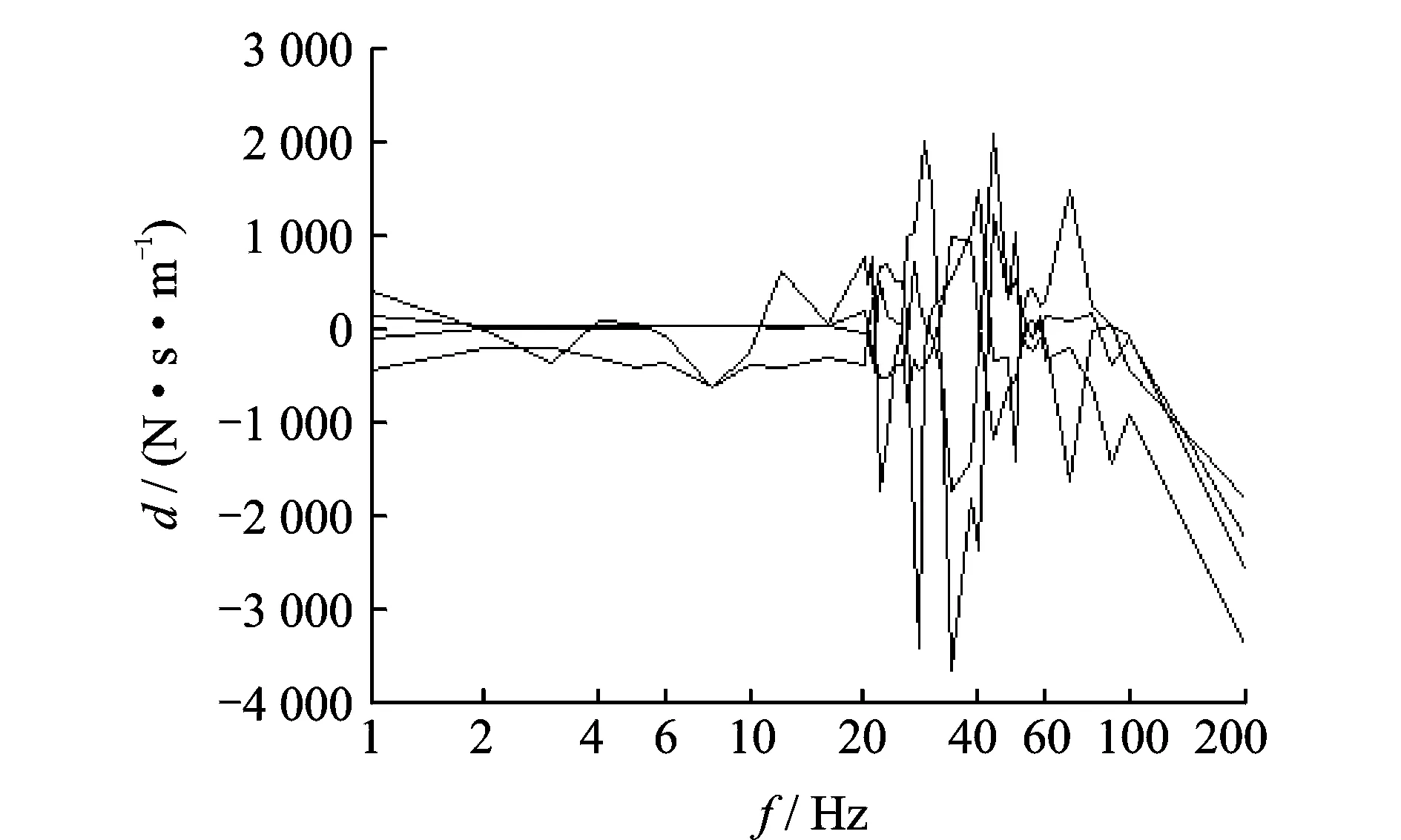
图7 上电磁轴承激励得到的4个方向等效阻尼测试结果

为了检验上述的测量结果，用下侧电磁轴承施加激励重复进行前面的测试实验，得到4个方向上的等效刚度和等效阻尼的测试结果分别如图8和图9所示。

根据两次实验测量可知，用上侧和下侧电磁轴承施加激励，得到的4个方向的等效刚度和等效阻尼的测试结果是相互吻合的。

从图6和8可知，电磁轴承的等效刚度随频率升高而逐渐增大，这与目前电磁轴承刚度特性的理论研究和实验研究文献的结论是一致的，即采用PID控制的电磁轴承，其等效刚度随频率递增。另外，值得注意的情况是等效刚度测量结果在20 Hz和60 Hz频率段中波动较大，有多个下凹的缺口。分析其主要原因：(1) 在靠近转子的固有模态频率时，转子振动特性随频率变化剧烈。并且，转子各方向的固有模态频率彼此有差异，但较接近，互相耦合影响，导致在20～60 Hz频率段的振动较为混乱，信号获取随频率变化剧烈。(2) 在转子的固有模态频率附近，转子的振动幅值较大，使得电磁轴承控制电流增大。由于实验装置中的两个电磁轴承的控制采用了差动结构，当控制电流大于偏置电流后，电磁力只靠单侧线圈产生。因此，等效刚度理论上会衰减一半。对于电磁轴承刚度在固有模态频率点会降低的现象，文献[15]在单自由度的刚度测试实验中就已经观察到。

图8 下电磁轴承激励得到的4个方向等效刚度测试结果

图9 下电磁轴承激励得到的4个方向等效阻尼测试结果

从图7和9可知，电磁轴承的等效阻尼在低频端变化不大，频率升高后，等效阻尼反而会下降。这个变化规律也是和目前研究文献的结论是吻合的。同样也可看到，等效阻尼在转子模态频率点的测量值也有波动。从图7和9中还可注意到，电磁轴承等效阻尼在频率升高后，等效阻尼下降出现负值。一般认为，传统机械轴承的阻尼是不可能出现负值的，而电磁轴承的支承特性可根据控制策略进行调节。电磁轴承的阻尼主要由控制策略的微分环节强弱决定。

本实验中发现电磁轴承的阻尼为负值的情况。电磁轴承的悬浮使转子外阻尼为零，而电磁轴承控制中的微分环节是对速度的控制作用，具有阻尼的特性，称为内阻尼。研究发现，如果电磁轴承控制采用PD控制(比例微分控制)，那么其支承阻尼值始终为正值。如果控制中含有积分环节，如PID控制，或有类似积分环节，那么无论是理论计算还是实际测试，其阻尼值都有可能出现负值。在文献[1、2、5、11、14、15]的电磁轴承特性研究中，都涉及了等效阻尼为负值的情况。由于本文着重论述和分析的是测量方法本身，对于电磁轴承出现负值等效阻尼的问题，篇幅所限，只予以简要介绍，恕不展开讨论。

根据实验的实际情况，在大多数频率段(指固有模态频率以外的频率段)，转子振动信号的幅值和相位的测量都具有非常好的稳定性和重复性，测试效果非常好。在转子的固有模态频率段时，由于转子振动随频率变化剧烈，测量读数会比较不稳定，必须适当减小激励幅度，以控制转子振动在一个适当的程度，激励实验可正常进行。

6 结 论

本文首先分析了多自由度刚性转子系统在电磁轴承支承条件与传统机械轴承的差异和共性，以及用等效刚度和等效阻尼描述电磁轴承-转子系统支承特性的适用范围。然后，提出了一种基于多自由度转子模型的，在转子悬浮条件下，对转子径向支承等效刚度和等效阻尼参数进行测量的方法。

实验结果表明，该方法是可行的，能够直接测量电磁轴承-转子系统在不同频率下的等效刚度和等效阻尼，真实地反映电磁轴承支承特性的实际情况，对于不同结构的电磁轴承-刚性转子系统具有普遍的适用性和可操作性，具有较强的实用意义。

参考文献：

[1] Tsai N, Li H, Lin C, et al. Identification of rod dynamics under influence of active magnetic bearing[J]. Mechatronics, 2011, 21(4): 1 013—1 024.

[2] Lim T, Cheng S. Parameter estimation and statistical analysis on frequency dependent active control forces[J]. Mechanical Systems and Signal Processing, 2007, 21(5):2 112—2 124.

[3] Kim S, Lee C. On-line identification of current and position stiffness by LMS algorithm in active magnetic bearing system equipped with force transducers[J]. Mechanical Systems and Signal Processing, 1999, 13(5): 681—690.

[4] Mehmet N, Matthew O, Cole T, et al. On the use of Schroeder phased harmonic sequences in multi-frequency vibration control of flexible rotor/magnetic bearing systems[A]. Proceedings of 8th International Symposium on Magnetic Bearings[C]. Mito, Japan, 2002:218—222.

[5] Lim T, Cheng S, Poh C. Parameter estimation of one-axis magnetically suspended system with a digital PID controller[A]. Proceedings of 1st International Conference on Sensing Technology[C]. New Zealand, 2005:419—424.

[6] Bauomy H. Stability analysis of a rotor-AMB system with time varying stiffness[J]. Journal of the Franklin Institute, 2012, 349(2): 1 871—1 890.

[7] Sayyad F, Gadhave N. Variable stiffness type magnetic vibration absorber to control the vibration of beam structure[J]. Journal of Vibration and Control, 2013, 7:1—7.

[8] 虞烈. 可控磁悬浮转子系统[M]. 北京：科学出版社. 2003.

[9] 胡业发，周祖德，江征风. 磁力轴承的基础理论与应用[M]. 北京：机械工业出版社. 2006.

[10] 赵雷，张德魁，杨作兴. 电磁轴承的最优刚度与系统结构参数间的关系[J]. 机械工程学报, 2000, 36(12):62—64.Zhao Lei, Zhang Dekui, Yang Zuoxing. Study on relationship between optimal stiffness and the structure parameter of AMB[J]. Chinese Journal of Mechanial Engineering, 2000, 36(12):62—64.

[11] 吴春华，胡业发，江征风. 磁力轴承支承特性的影响因素研究[J].设计与研究, 2007, (4):7—10.Wu Huachun, Hu Yefa, Jiang Zhengfeng. Study on Effect Factor for Magnetic Bearing Suspension Characteristic[J]. Design and Research, 2007, (4):7—10.

[12] 杨作兴，赵雷，赵鸿宾. 电磁轴承动刚度的自动测量[J]. 机械工程学报, 2001, 37(3):25—29.Yang Zuoxing, Zhao Lei, Zhao Hongbi. Automatic measurement of dynamic stiffness for active magnetic bearings[J]. Chinese Journal of Mechanial Engineering, 2001, 37(3):25—29.

[13] 赵晶晶，周燕，时振刚，等. 电磁轴承刚度阻尼自动测试[J]. 机械工程学报, 2010, 46(20):48—52.Zhao Jingjing, Zhou Yan, Shi Zhengang, et al. Automatic measurement of stiffness and damping of active magnetic bearings[J]. Chinese Journal of Mechanial Engineering, 2010, 46(20):48—52.

[14] 左从杨，周瑾. 控制参数对转子振动电磁阻尼器的等效刚度阻尼的影响[A]. 第4届中国磁悬浮轴承学术会议[C].上海，2011:59—63.Zuo Chongyang, Zhou qing. Control Parameter's Influence on Equivalent Stiffness and Damping of Magnetic Damper for Rotor Vibration Control[A]. The 4th Chinese Symposium on Magnetic Bearings(CSMB4)[C]. Shanghai, 2011:59—63.

[15] 蒋科坚，祝长生. 未知传递函数情况下主动电磁悬浮系统支承特性在线测定[J]. 中国机械工程, 2010, 21(8): 883—888.Jiang Kejian, Zhu Changsheng. On-line measurement of supporting characteristic of active magnetic levitations with unknown transfer function[J]. Chinese Mechanial Engineering, 2010, 21(8): 883—888.

[16] 蒋科坚，祝长生. 基于不平衡识别的主动电磁轴承转子系统自动平衡[J]. 振动工程学报, 2009, 22(6):559—564.Jiang Kejian, Zhu Changsheng. Auto balance of active magnetic bearings supporting rotor system by means of unbalance identification[J]. Journal of Vibration Engineering, 2009, 22(6):559—564.