基于空腔流动特性的汽车侧窗风振噪声控制方法研究

谷正气 ， 王 宁,2， 汪怡平， 张 勇 ， 刘龙贵

(1.湖南工业大学机械工程学院， 湖南 株洲 412007;2.湖南铁道职业技术学院铁道牵引与动力学院， 湖南 株洲 412001； 3.武汉理工大学汽车工程学院， 湖北 武汉 430070)

引 言

驾驶员长期在车内驾驶时，由于车内环境较为封闭，空气得不到更新，很容易使驾驶员感到疲倦，这时如果打开车窗就可以有效地改善车内的空气环境，缓解驾驶疲劳。但是打开车窗时很容易产生风振噪声，这是一种频率很低但是强度很高的气动噪声[1]，虽然它不易被人耳听到，但它产生的脉动压力却使驾驶员感到烦躁，进而会影响驾车的安全性。因此，为了确保驾驶员的乘坐舒适性和驾驶安全性，在汽车设计阶段考虑风振噪声的控制十分必要的。

对风振噪声的研究始于20世纪60年代，Bodger和Jones率先开展了客车后窗开启时的风振噪声研究[2]。他们指出当侧窗开启时，整个车厢形如Helmholtz共振腔，当气流流经窗口时，产生涡的脱落，进而产生共振，并从理论上提出了三种解决风振噪声的办法；Karbon等人采用非结构化网格和基于有限元法的商用CFD软件对汽车模型进行了仿真分析，获得了与风洞实验结果较吻合的结果[3～5]；Sovani和Hendriana利用CFD软件对某乘用车的侧窗风振噪声进行了研究，得到的仿真结果与实验值差别很小[6]；An等利用CFD软件对某SUV的侧窗风振噪声进行了仿真分析，分析了若干变量对风振噪声的影响，并采取了一些措施来降低后窗的风振噪声[7,8]；湖南大学汪怡平也对汽车风振噪声进行了深入研究，推导出了弱可压缩湍流模型，较为准确地预测了车内风振噪声[9,10]。

前人在研究风振噪声控制方法时，仅提出了一些能够控制风振噪声的方案，没有对方案的机理进行分析，也未对其优化。本文运用CFD方法，针对文献[9]中提到的一种在后窗附近加凹槽来控制风振噪声的方法，结合空腔理论着重阐述了凹槽控制噪声的机理，并对其进行了实车数值仿真计算[11]，结果表明，开式空腔形式的凹槽对风振噪声的控制最为明显。

1 大涡模拟的控制方程

将Navier-Stokes 方程在物理空间进行过滤得到流体LES控制方程[9]

(1)

(2)

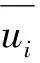
为使控制方程封闭，当前，采用较多的亚格子模型是涡旋黏性模型

(3)

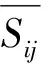
2 空腔噪声计算方法

2.1 空腔噪声数值仿真

汽车侧窗开启时,形状类似于一个开口空腔，为了节约计算资源，且能达到预测风振噪声计算方法的目的，本文选择了一个抽象的简易车厢模型进行仿真分析，整个计算模型形如一个开口的空腔，类比于侧窗开启时的车内乘员舱。如图1所示，模型的长、宽、高尺寸为3.2 m×1.4 m×1 m，车窗开口位于车厢中央，尺寸为0.1 m×0.24 m×0.015 m，监测点位于车厢底部正中央。并对其进行网格划分，网格总数约为320万(图2)，其中附面层第一层的厚度为0.1 mm，并以1.2的比例逐层生长。

本文使用CFD软件Fluent对简易车厢模型进行计算仿真，在进行瞬态计算之前，通常先进行稳态计算，并以此稳态计算得到的结果作为瞬态计算的初始值。在本文的计算中，稳态计算选用realizablek-ε模型，边界条件的具体设置如表1所示。

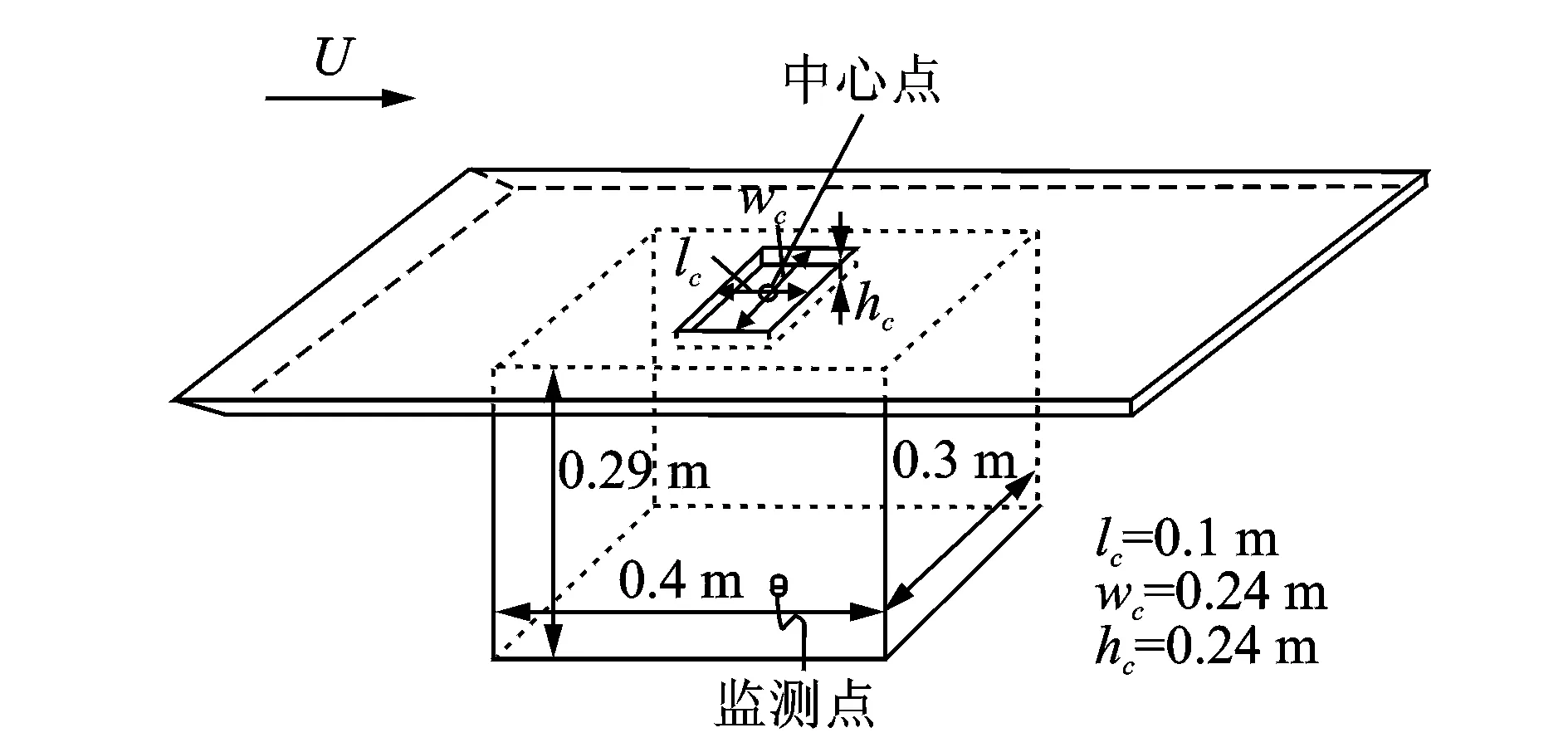
图1 简易车厢的几何模型以及噪声监测点的位置

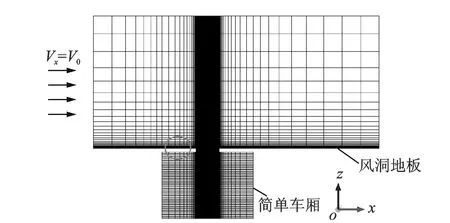
图2 计算域的纵对称面上的网格分布图

表1 计算域边界条件设置

稳态求解器具体设置如表2所示。瞬态计算的湍流模型采用LES计算模型，具体设置见表3。

表2 稳态计算求解参数设置

表3 瞬态计算求解参数设置

瞬态计算的时间步长设为0.002 s，计算总时长为1 s。由于瞬态计算时流场有一个逐步的过程，最后取用的是0.2～1 s的稳定后数据。

2.2 空腔噪声实验

图3 风洞中的模型安装示意图

本文实验是在美国普度大学的Herrick低噪声风洞中完成。实验所用的噪声测试设备为：比利时LMS公司Test.Lab系统。该系统集成了Test Lab 7A实验分析软件系统及16通道SCADAS便携式数据采集前端；丹麦B&K公司的1/4英寸电容式4136型传声器与B&K2609型前置放大器。图3为安装在风洞中的简易车厢箱体。厢体由两根横梁托住，并保持其顶端开口的上表面与风洞的下地板平齐，传声器固定于厢体的底部中心，且其头部与厢体底面平齐。模型安装完毕后，开启风机，风速为25 m/s。

2.3 仿真数据和实验数据对比分析

将仿真结果与实验结果进行了对比，如图4和5所示。

由图4，5所示，同一个监测点处，实验结果显示共振点处频率为103 Hz，声压级为123 dB；仿真结果显示共振频率在123 Hz，声压级达到了120 dB。实验值的谐振很明显，首先最高值出现在第一个峰值点，在0～500 Hz的频段内出现了4个峰值点，且呈现出依次减弱的态势，而使用LES模型仿真所得到的频谱图谐振不是很明显，LES模型在整个频段上出现了4个峰值点，第三个峰值点处声压级最大。综上，在整个频率段内仿真数据与实验数据基本吻合，说明本文采用的网格方案及仿真方法的可靠性。造成误差的原因主要有以下3方面：1.风洞实验和数值仿真在边界条件设置时存在差异，如湍流模型等；2.本文将空气类型看作是理想气体，和真实的气体状态存在一定的差别；3.测量精度、温度、压强等环境因素的影响。

图4 仿真得到的监测点处声压频谱图

图5 实验得到的监测点的声压频谱图

3 控制方案及其机理研究

在对空腔噪声计算方法研究的基础之上，本文使用简单的空腔模型，通过单个空腔和串联空腔对比的方法，对串联空腔的降噪机理进行了研究。由文献[10]可知空腔噪声是反馈机制和声共振共同作用的结果，而空腔噪声的产生又和气流的流动有着密切的关系，不同的气流流态所引起的风振噪声大小也各不相同。下图所示为单个空腔和串联空腔的流线图、湍动能云图和同一接收点处声压级对比图。

由图6所示单个空腔的流线图可知，气流流经上边缘时产生气流分离，一部分气流形成涡旋，并未生长完成就冲击到了底面和上边缘的壁面，另一部分气流直接冲击到空腔的下边缘。由图8的湍动能云图可知，气流回旋处和下游气流直接冲击处的湍动能比较大；当加入串联空腔之后(图7)，空气在前腔体中形成涡旋，将气流向上导出，使气流在流经后面空腔的时候，大部分的气流回旋在腔体中，且涡旋得到了充分的成长，只有小部分的气流直接撞击后边缘，在整个过程中也使进入后空腔的能量减少了很多(图9)。由图10所示的声压级对比图可知串联空腔的声压级要比单个空腔低5 dB左右。

图6 单个空腔纵对称面上流线图

图7 串联空腔纵对称面上流线图

图8 单个空腔纵对称面上的湍动能云图

图9 串联空腔纵对称面上的湍动能云图

图10 接受点处声压级

由上述分析可知，串联空腔的加入，一方面将一部分向后流动的气流从后空腔中导出，另一方面减少了引起空腔共鸣的能量。这样做不但减弱了气流的反馈作用，而且也减少空腔产生共振能量，从而起到了有效地控制风振噪声的作用。

4 控制方案实车数值模拟

4.1 计算域和网格化分

在前述对串联空腔研究的基础之上，将其应用到实车之上，即在B柱上加一个凹槽，使凹槽和开后窗后的车内空间形成一个串联空腔。本文所用的轿车模型见图11，在不影响计算精度的情况下，对车身进行了简化处理，省略了车灯、门把手、天线等，并将轿车底部简化为平面，模型长L=4 700 mm，宽W=1 740 mm，高H=1 470 mm。图11为凹槽的形状和位置，图12为其局部放大图，凹槽的形状尺寸为L/D=5开始空腔，L=100 mm，D=20 mm。

图11 凹槽的形状及其位置

图12 凹槽横截面的局部放大图(单位：mm)

计算域为包围汽车模型的长方体(图13)长11L，宽5W，高约4H。图14为车身表面网格分布图，车身处使用密度盒进行局部加密，生成局部精细的网格。本文采用四面体网格，网格数量7×106万左右，为了模拟附面层效应，在车身表面，生成了三层精细的棱柱网格。

本文使用前述经实验验证过的计算方法对实车模型进行了数值仿真，风速为30 m/s，监测点选择在驾驶员的左、右耳旁，其具体坐标为：(1.586 m，-0.463 m，0.804 m)、(1.586 m，-0.281 m，0.804 m)。采样时间设为2 s，由于流场从开始计算到稳定需要一个过程，因此只记录1～2 s的时域信号；时间步长决定了能计算的最高频率，风振噪声主要集中在低频[10]，所以本次计算的最高频率设定在250 Hz，为了便于观察，图形最高频率只显示到100 Hz(图22，23)，时间步长为0.002 s，因此总步数为1 000步，每时间步迭代20次。

图13 计算域模型

图14 车身纵对称面上的网格分布图

4.2 计算结果分析

4.2.1 车内空腔速度场和湍动能分析

由前述空腔控制机理可知，串联空腔控制气动噪声是气流的导出效应和能量耗散效应的结合。

图15，16为原车和加凹槽车z=0.804 m截面位置稳态的流线图和速度云图。图15中由于气流直接从后窗进入车内，后排座附近气流流速较高，且形成很多较大的涡旋，当气流在车内回旋流向前排时，气流流态非常复杂，驾驶员和副驾驶周围存在较多的涡旋，气流在此处的流速和流量也都比较大；由图16可知，加入凹槽后，由于凹槽对气流的干扰作用，气流从后窗流入车内的路径被改变，气流直接流向了乘员舱后部，再回旋至前排，云图显示进入车内气流的流速明显减小，且涡旋大小和数量都比原车有所减少。气流流量和流速的减小必然导致驾驶员耳旁声压级的降低。

图15 原车横截面上速度云图

图16 加凹槽后横截面的速度云图

图17，18为原车和开槽后车横截面上的湍动能云图。研究表明，气流流经车体表面时，由于A柱的阻挡，在其后部形成强烈的湍流后再次附着在侧窗表面形成层流[9]。由图17可知，由于后窗附近为层流附面层，因此进入车内的能量较多。由图18可知，加入凹槽后，使后窗附近的层流边界层转化为湍流边界层，一部分能量在这个过程中耗散，使得进入到乘员室内的湍动能的强度和面积与原车相比都有所减少，进而引起空腔共振的能量也减少了很多，风振噪声得到了有效地抑制。这和文献[10]中提到的湍流边界层引起空腔噪声的声场强度比层流弱的原理相吻合。

图17 原车横截面上湍动能云图

图18 加凹槽后横截面的湍动能云图

4.2.2 车内空腔压力场分析

汽车在开启后窗时，乘员舱相当于一个有一定体积的空腔，不能完全等同于一个开口空腔。外部气体的运动能量通过侧窗开口处的空气传入车内空腔，车内的空气如同“弹簧”一样被压缩、膨胀，气流速度越高、车内压力范围波动越大，气体的压缩与膨胀过程就越剧烈，引起的风振噪声相应地也会更高。

如图19，20所示原车开启左后窗时和加凹槽车开启左后窗时z=0.75 m截面位置稳态压强云图对比。由图19可知，车身两侧都为负压区，一部分气流直接撞击到C柱前缘，在局部形成一个高压区；另一部分气流则从左侧后窗进入车内，使车内压力波动较大。由图20可知，B柱加入凹槽后，使得压强在后窗附近形成高低交替的状态，车外负压区域有所减少，车内压力波动的范围也有明显的减小。图21为原车与加凹槽后驾驶员左耳处脉动压力对比，监测点处脉动压力最大降低了150 Pa。

图19 原车横截面上压力云图

图20加凹槽后横截面的压力云图

图21 原车与加凹槽后驾驶员左耳处脉动压力对比

图22 原车与加凹槽之后驾驶员左耳处声压级对比

将原车与加凹槽后车的声压级计算结果进行对比，如图22所示。原车在开启后窗时的风振噪声峰值在129 dB，加凹槽之后的风振噪声峰值在117 dB，风振噪声降低了12 dB，可见凹槽的加入对汽车侧窗的风振噪声起到了抑制作用。

由上述分析可知，凹槽的加入减小了车内压力波动范围，同时也降低了车内气体的流速和湍动能。对汽车后窗风振噪声起到了很好的抑制作用。

5 控制方案优化

空腔流动类型主要受其长深比(L/D)决定，依据不同L/D下腔内的静态压力分布将空腔分为三种类型，即闭式空腔 (L/D>13)、过渡式空腔(10≤L/D≤13)和开式空腔(L/D<10)[11]。

本文前述所使用的凹槽L/D=5，属于开式空腔，为了更好研究凹槽对车内起到噪声的影响，需要对其他两种形式的空腔也进行数值模拟计算。本文在此选取了L/D=12的过渡时空腔和L/D=14的闭式空腔。如图23为三种空腔形式的驾驶员左耳旁声压级频谱图。

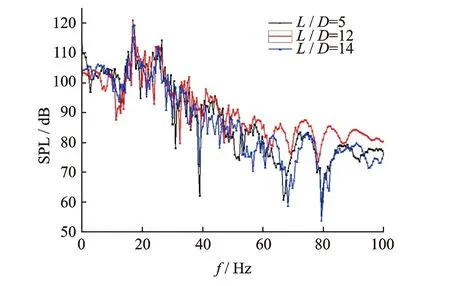
图23 三种不同形式凹槽的声压级频谱图

由图23可知，三种不同形式下的风振噪声最大值频率都在17 Hz，而L/D=12时的风振噪声最大，达到了121 dB；L/D=5时最小，只有117 dB； 当L/D=14时为119 dB。可见当凹槽形状为开式空腔时降噪效果最明显。

开式空腔的的范围是L/D<10，为了找出凹槽控制车内风振噪声的最优化方案。本文选取不同尺寸下的凹槽进行数值模拟，计算结果如表3所示。

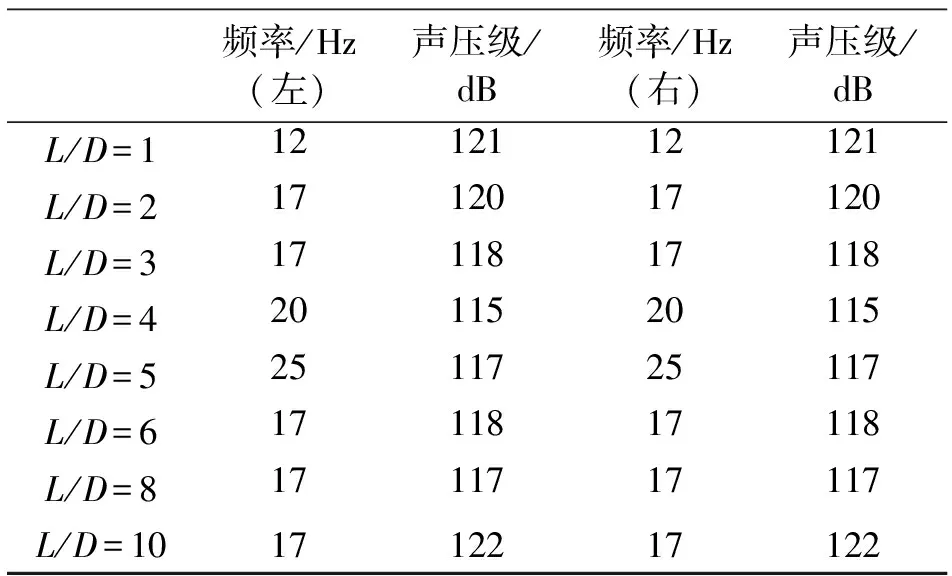
表3 不同尺寸下风振噪声声压级对比

由表3可知，当L/D=1时风振噪声达到121dB，并随着L/D的增加而逐渐减小；当L/D=4时，声压级最小，为115dB，这时声压级开始随着L/D在增加而增大；到L/D=10时，声压级增加到122dB。由此可见L/D=4的长深比对控制风振噪声最为有利。

6 结 论

通过对凹槽控制车内风振噪声的机理研究，并对不同形式的凹槽进行的对比分析，可得出以下结论：

(1)原车的侧窗风振噪声峰值处于一个较高的水平，噪声压级达到129dB(14Hz)。

(2)凹槽对实车风振噪声的控制主要是通过降低进入车内气流的流速和湍动能，减小乘员舱内部的压力脉动来实现的。

(3)通过在B柱上加一个凹槽的方法可以有效地控制汽车侧窗的风振噪声。对不同尺寸的凹槽的进行对比分析后发现，L/D=4的开式空腔对风振噪声的抑制明显，最大降幅14dB。

参考文献：

[1] 谷正气,肖朕毅,莫志姣.汽车风振噪声的CFD仿真研究现状[J].噪声与振动控制,2007，8(4)：65—68.GU Zhengqi , XIAO Zhenyi, MO Zhijiao. Review of CFD simulation vehicle wind buffeting[J].Noise and Vibration Control,2007，8(4):65—68.

[2] Bodger W K, Jones C M． Aerodynamic wind throbin passenger cars[R] . SAE Technical Paper 640797,1964.

[3] Karbon K J, Kumarasamy S. Computational aero acoustics applications in automotive design[A]．First MIT Conference on Computational Fluid and Solid Mechanics[C]． Boston,USA,2001:871—878.

[4] Karbon K J, Kumarasamy S, Singh R. Applications and issues in automotive computational aeroacoustics [A]. Proceedings of the 10th Annual Conference of the CFD Society of Canada[C]. Taylor & Francis,2002：25—28.

[5] Karbon K J, Singh R K. Simulation and design of automobile sunroof buffeting noise control[A]. Proceedings of the 8th AIAA/CEAS Aeroacoustics Conference & Exhibit[C]．2002:23—24．

[6] Sovani S D, Hendriana D. Predicting passenger car window buffeting with transient external aerodynamics simulation[A]． Proceedings of the 10th Annual Conference of the CFD Society[C]．2002:130—143．

[7] An C F, Mitchell M, Puskarz, et al. Attempts for reduction of rear window buffeting using CFD [R].SAE Technical Paper 2005-01-06 03,2005.

[8] An C F, Alale S M, Sovani S D, et al. Side window buffeting characteristicso fan SUV [R]. SAE Technical Paper 2004-01-0230,2004.

[9] 汪怡平.汽车风窗噪声与风振噪声的机理及控制方法研究[D].长沙：湖南大学，2011.WANG Yiping. Comprehensive study of generation mechanism and reduction methods of vehicle wind rush noise and buffeting noise [D].Changsha: Hunnan University,2011．

[10] 汪怡平.汽车气动噪声分析与控制[D]. 长沙：湖南大学，2009.WANG Yiping. The numerical analysis and controlment for the automotive eaerodynamic noise[D]. Changsha:Hunnan University，2009.

[11] 张强.流动诱导空腔振荡频率方程的改进[J].振动工程学报，2004,17(1):53—57．Zhang Qiang. Development of the frequency equation used for prediction of fluid induced pressure oseillation in cavities[J] .Journal of Vibration Engineering, 2004,17(1):53—57．