轴对称横观各向同性饱和土中单桩竖向振动的简化模型求解
高洪波
(信阳师范学院土木工程学院,河南 信阳 464000)
引 言
桩基在许多工程领域有着广泛的应用。由于桩基承受地震激励、风荷载等动态激励的作用,对于桩基在动态荷载作用下力学特性的研究就显得十分重要,不少学者相继对桩基的振动特性进行了研究。目前针对均质单相土介质和均质饱和土中桩基振动问题已有不少的研究,Nogami T等将土层视为均质黏弹性介质研究了桩-土之间的竖向动力相互作用[1,2],并在时域内研究了单桩的轴向动态响应;Novak M等对线黏弹性土层中桩基的水平振动进行了研究[3];Militano G等在考虑瞬态扭转和轴向力的作用下[4],研究了层状土体中桩基的动态响应问题;李强等和Wang JH等基于Biot饱和土理论[5,6],分别对饱和土中单桩和群桩的纵向振动特性进行了研究;Orlando M等提出了两相饱和土中群桩的三维有限元模型[7],并对饱和土中群桩的振动特性进行了研究;张智卿等研究了三维饱和土中端承桩的扭转耦合振动问题[8]。
天然土体由于其粘土颗粒及其组构单元排列造成了土体的各向异性,土体在沉积过程中,由于扁平介质颗粒排列的取向性,土体竖向和水平向的性质存在着差异,往往会形成层状结构的粘土层,相互交错的薄层矿物成分及物理力学性质各不相同,横观各向同性力学模型比较符合天然土体的这一特性[9]。因此,为了较为合理准确地研究天然土体中桩基的动态特性,需要考虑土体的横观各向同性效应。然而,针对横观各向同性饱和土中桩基振动问题的研究较少,张智卿等利用Biot饱和土理论描述土体的力学特性[10],对轴对称横观各向同性土体中桩基的扭转振动进行了初步研究。由于当桩-土体系作竖向振动时,饱和土层固相骨架的径向位移和环向位移相对较小[1],参照单相土-桩的研究假定,这里忽略土体径向位移和环向位移的影响。本文借助饱和多孔介质理论研究横观各向同性饱和土中单桩的竖向振动问题。
1 横观各向同性饱和土层竖向振动简化模型及控制方程
桩周土视为横观各向同性饱和土,忽略流相和固相间的质量及能量交换,则饱和土的流固混合物动量方程,孔隙流体动量方程及体积分数方程可分别表示为[11,12]
(1)
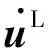
TS=-nSpI+TSE,TF=-nFpI+TLE,pF=-pS=pgradnF+pLE
(2)
式中TSE,TLE为固相土骨架和液相的有效应力张量,pLE为额外数量,p为饱和土的有效孔隙水压力。通常假设TLE=0,体积分数nS和nF满足平衡方程nS+nF=1。
对于横观各向同性介质,其应力应变关系为[13]
σr=C11εr+C12εθ+C13εz
(3)
σθ=C12εr+C11εθ+C13εz
(4)
σz=C13εr+C13εθ+C33εz
(5)
τθz=C44γθz,τrz=C44γrz,τrθ=C66γrθ
(6)
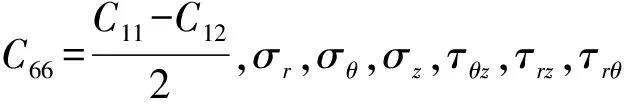
(7)
同时,额外数量pLE满足
(8)
式中sν为耦合系数, 它描述固相和液相的耦合作用。
由式(1)~(8)可得横观各向同性饱和土层的竖向振动控制方程为
(9)
(10)
(11)
2 横观各向同性饱和土层竖向振动的求解
在桩顶简谐荷载的作用下,桩-土作简谐振动,由于方程左右两边都存在eiωt项,在以后的计算中去掉eiωt项,由式(9)~(11)得
(12)
(13)
(14)
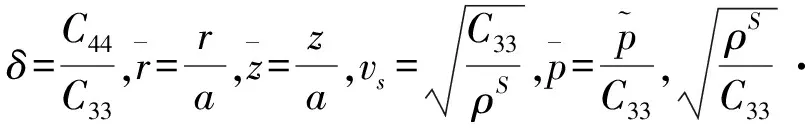
(15)
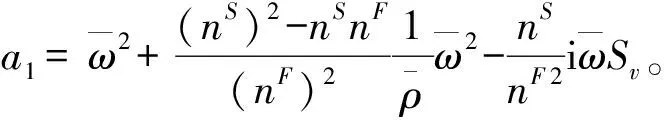
(16)
(17)
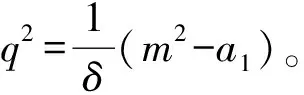
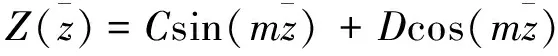
(18)
(19)
考虑到无穷远处应力和位移为零的条件,可知B=0。由饱和土体表面应力为零得D=0。由此可得
(20)
(21)
对方程(20),(21)两边积分,并考虑土层水平方向无穷远处位移为零,得
(22)
(23)
由式(13),(14)求得
(24)
综上所述,可以将位移和剪应力写成级数的形式
(25)
(26)
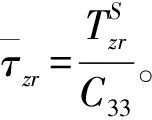
3 桩的竖向振动求解
考虑式(26),很容易建立无量纲化的横观各向同性饱和土中单桩的竖向振动控制方程为
(27)
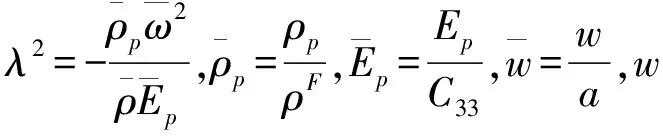
(28)
E1,E2为待定系数,可由桩端的边界条件求得。设桩端的边界条件为
(29)
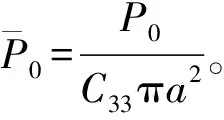
由此可得
(30)
假设桩土完全接触,则接触面处桩基和土体的位移相等,则有
(31)
利用三角函数的正交性
(32)
可得
则非齐次方程(27)的解为
(33)
由桩的竖向位移可以求出桩身任一点的分布力,进而可以得到桩顶位移频率响应函数为
(34)
由桩顶复刚度的定义可得桩的复刚度为
(35)
4 数值算例与讨论
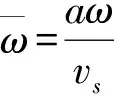
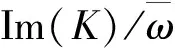
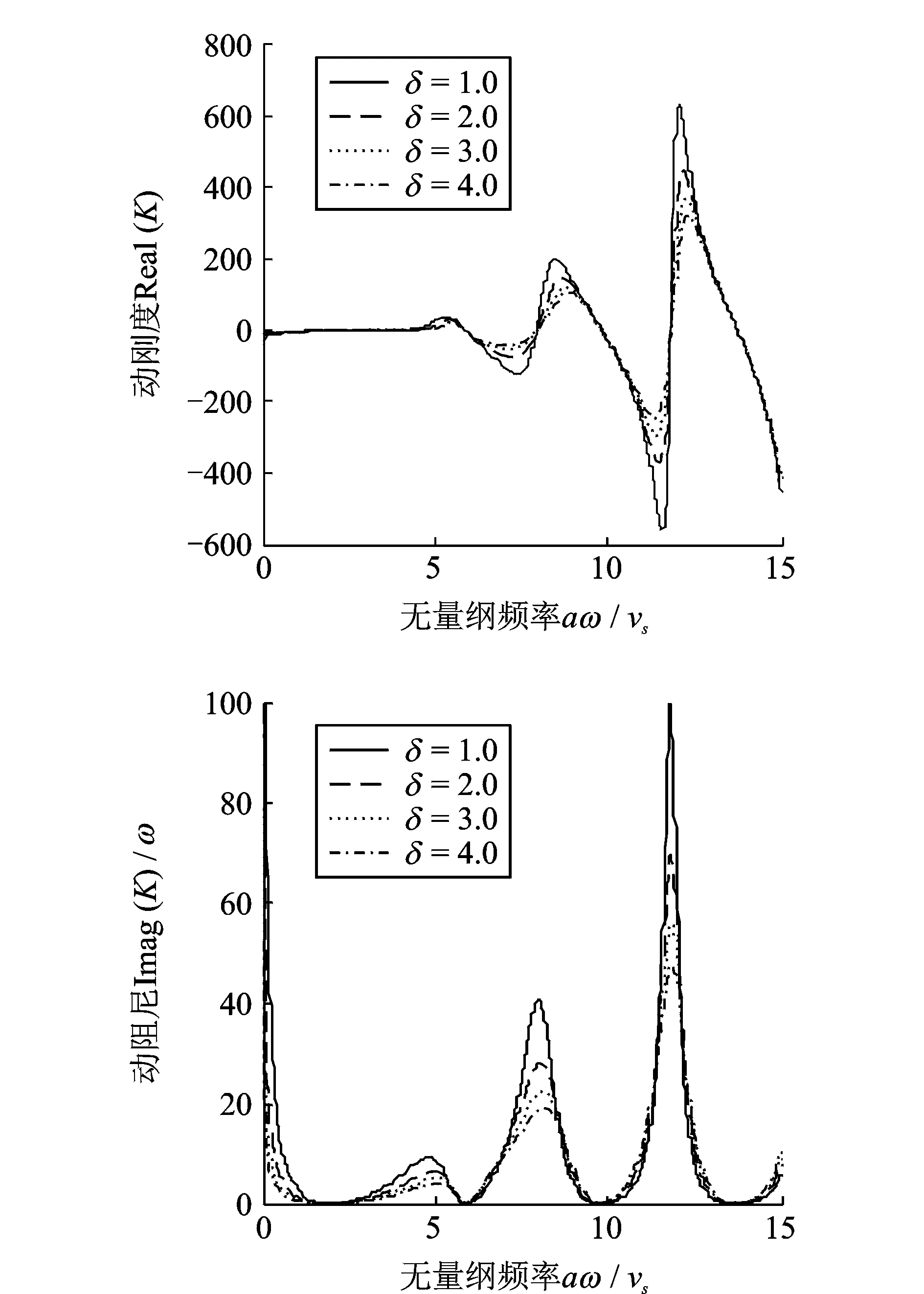
图1 各向异性参数δ对桩顶复刚度的影响
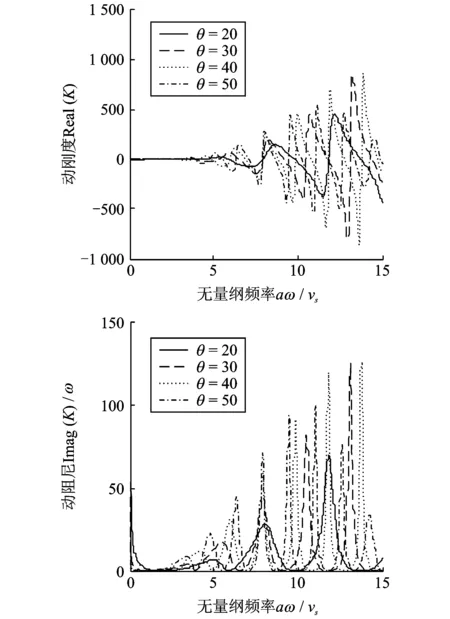
图2 长径比对桩顶复刚度的影响
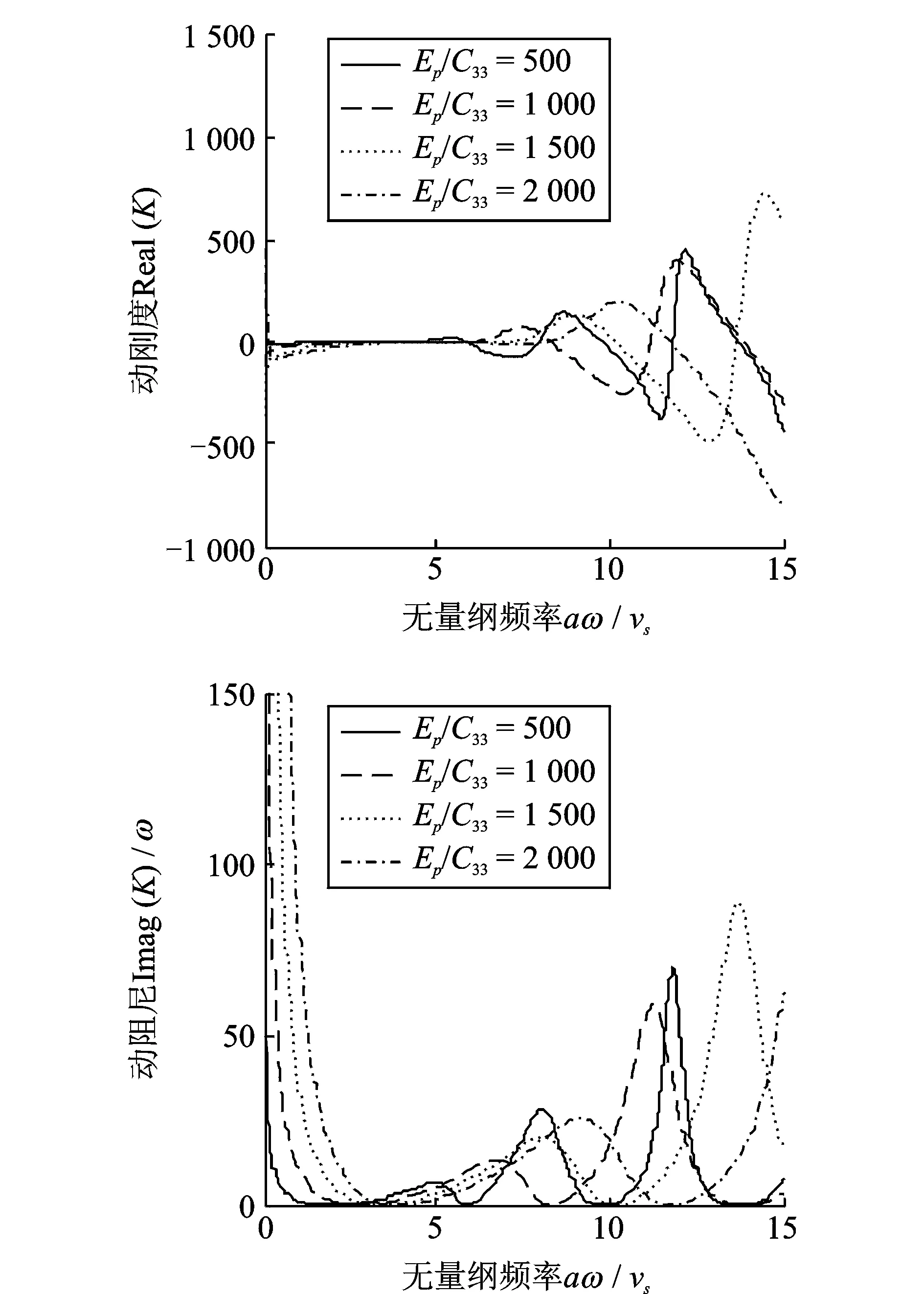
图3 模量比对桩顶复刚度的影响
5 结束语
为了考虑横观各向同性效应对饱和土体中单桩竖向振动的影响,将桩周土体视为横观各向同性介质,针对横观各向同性饱和土中单桩的竖向振动问题进行了研究分析,得到的结论主要有:1)横观各向同性参数对桩顶竖向复刚度的影响较为复杂,在低频和高频时对动刚度的影响存在差异,在低频时各向同性参数对动刚度几乎没有影响,在高频时各向同性参数越大,动刚度越小;而动阻尼随着各向同性参数的增大则减小;2)长径比的大小对桩基的振动影响规律不一样,当长径比小于临界长度时,长径比对桩基振动有较大的影响,而当长径比超过临界长度时,由于长径比较大,桩基抵抗共振的能力较强,所以长径比较大时对桩基振动影响不大;3)由于土体的横观各向同性对饱和土中单桩的竖向振动有影响,所以,对于天然地基中桩基的抗震设计和检测,应尽量考虑土体的各向异性对桩振动特性的影响。
[1] Nogami T, Novak M. Soil-pile interaction in vertical vibration[J]. Earthquake Engineering and Structural Dynamics, 1976, 4(3): 277—293.
[2] Nogami T, Konagai K. Time domain axial response of dynamically loaded single piles[J]. Journal Engineering Mechanics, 1986, 12(11):1 241—1 252.
[3] Novak M, Nogami T. Soil-pile interaction in horizontal vibration [J]. Earthquake Engineering and Structural Dynamics, 2006, 5(3): 263—281.
[4] Militano G,Rajapakse R K N D. Dynamic response of a pile in a multilayered soil to transient torsional and axial loading[J].Geotechnique, 1999, 49(1): 91—109.
[5] 李强,王奎华,谢康和,饱和土中端承桩纵向振动特性研究[J].力学学报,2004, 36(4):435—442.Li Qing, Wang Kuihua, Xie Kanghe. Vertical vibration of an end bearing pile embedded in saturated soil [J]. Acta Mechanical Sinica,2004, 36(4):435—442.
[6] Wang J H, Zhou X L, Lu J F. Dynamic response of pile groups embedded in a poroelastic medium [J]. Soil Dynamics and Earthquake Engineering, 2003, 23(3): 235—242.
[7] Orlando Maeso, Juan J Aznarez, Fidel Grcia. Dyanmic impedances of piles and groups of piles in saturated soils [J]. Computer & Structures, 2005, 83(10/11): 769—782.
[8] 张智卿,王奎华,谢康和. 饱和土层中桩的扭转振动响应分析[J].浙江大学学报(工学版),2006, 40(7): 1 211—1 218.Zhang Zhiqing, Wang Kuihua, Xie Kanghe. Study on torsional vibration of pile embedded in saturated soil[J].Journal of Zhejiang University (Engineering Science), 2006,40(7): 1 211—1 218.
[9] 蔡袁强, 占宏, 郑灶峰, 等. 横观各向同性饱和土体振动分析[J]. 岩土力学,2005,26(12):1 917—1 920.Cai Yuanqiang,Zhang Hong, Zheng Zaofeng, et al. Vibration analysis of transversely isotropic saturated soils[J]. Rock and Soil Mechanics, 2005, 26(12):1 917—1 920.
[10] 张智卿,王奎华,靳建明. 轴对称横观各向同性土体中桩的扭转振动响应研究[J]. 振动工程学报,2011, 24(1):60—66.Zhang Zhiqing,Wang Kuihua,Jin Jianming. Torsional vibration of pile embedded in axisymmetric transversely isotropic soil[J]. Journal of Vibration Engineering, 2011, 24(1):60—66.
[11] R de Boer, Ehlers W, Liu Z. One-dimensional transient wave propagation in fluid-saturated incompressible porous media[J]. Archive of Applied Mechanics,1993, 63(1): 59—72.
[12] 杨骁,张燕.一维流体饱和粘弹性多孔介质层的动力响应[J].力学季刊,2005, 26(1):44—52.Yang Xiao,Zhang Yan.Dynamical response of one dimension liquid saturated viscoelastic porous medium layer[J]. Chinese Quarterly Mechanics, 2005, 26(1): 44—52.
[13] 黄小岗,黄义. 横观各向同性饱和层状地基的三维稳态动力响应[J].工程力学,2006, 23(5):132—138.Huang Xiaogang, Huang Yi. 3-D dynamic response of transversely isotropic saturated layered soils to an arbitrary harmonious source[J]. Engineering Mechanics,2006, 23(5): 132—138.
[14] 段靓靓,梁锴,方理刚.岩石各向横观同性参数试验研究[J].土工基础,2008, 22(3):80—85.Duan Liangling, Liang Kai, Fang Ligang. Test research for transverse isotropy parameter of rock[J].Soil Engr. and Foundation, 2008, 22(3):80—85.

