旋翼/机身耦合问题的CFD/CSD分析方法

陈全龙， 韩景龙， 员海玮

(南京航空航天大学机械结构力学与控制国家重点实验室， 江苏 南京 210016)

引 言

直升机乘坐舒适性要求的提高，对减小直升机振动水平提出了更高的要求。直升机的振动主要来自于旋翼系统及其与机身之间的相互耦合。旋翼/机身耦合系统的振动响应分析，是进行减振处理，降低全机振动水平的基础。

已有许多国外学者对直升机振动响应分析进行了研究。早期的工作大多是分别求出旋翼和机身的阻抗，令两者的阻抗在桨毂处匹配，进而求得机身的振动响应[1～3]。Warmbrodt和Friedmann最先建立了旋翼/机身耦合系统的非线性气动弹性响应分析模型，考虑了机身的6个刚体自由度[4]。Fledel通过有限元方法，对旋翼/机身耦合系统的振动响应进行了研究，考虑了旋翼与机体的运动和惯性载荷之间的相互耦合[5]。之后，Friedmann和Chopra等分别建立了旋翼/弹性机身的非线性气动弹性方程，采用梁单元建立了机身的三维有限元模型，对机身典型位置的振动响应进行了研究[6～9]。

准确的机身结构模型和旋翼流场分析，是直升机振动响应分析的关键。上述研究均采用准定常或半经验的二维气动力公式，机身则采用刚体模型或基于梁单元的简化模型，其分析精度还有待进一步提高。

近年来，随着计算机技术和计算流体力学(CFD)的迅速发展，基于非定常Euler/N-S方程的CFD方法，成为目前最有效的旋翼流场分析方法[10～12]。这为旋翼/机身耦合系统分析精度的提高，提供了新的思路。目前CFD方法已经用于求解单独旋翼的气动弹性问题，但对于旋翼/机身耦合系统的响应分析，由于问题难度更大，还未见到相关文献。

本文将CFD方法引入到旋翼/机身耦合系统的振动响应分析中，通过动态嵌套网格与动网格技术来实现桨叶网格的刚体运动和弹性变形，利用CSD软件建立精细的机身三维有限元模型，然后通过带配平的松耦合迭代方法求解系统响应。该方法能准确模拟机身结构和旋翼流场的特性，具有较高的分析精度和工程适用性。以某型两片桨叶跷跷板式直升机为算例，对悬停及定常前飞状态下，机身典型位置的振动响应进行了分析，将计算结果与实验值进行了比较，并考察了机身弹性对系统响应分析的影响。

1 计算方法及理论

1.1 旋翼/机身耦合动力学方程

旋翼为两片桨叶跷跷板式构型，桨叶采用15自由度的中等变形梁单元[13]。理论气动力采用准定常气动力模型和Drees线性入流模型。旋翼运动方程与机身方程通过桨毂中心点耦合在一起，旋翼载荷通过桨毂传到机身上，而机身的运动也会影响到旋翼载荷。

在常规的旋翼气动弹性响应分析中，仅考虑桨毂力常值部分对全机配平方程的影响，在定常前飞时，则假定机身固定不动。但桨毂力的谐波部分会使机身产生刚体运动，进而与旋翼运动发生耦合。因此，在机身振动水平分析中，还必须考虑机身的刚体运动自由度。

系统的动力学方程通过哈密顿变分原理得到

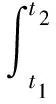
(1)

式中 δU为弹性能变分，δT为动能变分，δW为外力虚功。对这些能量有贡献的是桨叶和机身，各能量的变分可表示为：

(2)

(3)

(4)

下标b，F分别表示桨叶和机身，Nb表示桨叶片数。

此次分析中，通过MSC/Nastran软件建立机身的有限元模型，并根据模态试验结果，对有限元模型进行修正，以保证模型有足够的分析精度。然后将机身方程与旋翼方程组装起来，得到旋翼/机身耦合系统的动力学方程。

机身有限元模型如图1所示，机身主承力结构采用梁单元和壳单元，其他设备质量则采用集中质量单元分布到对应位置处。机身前10阶弹性模态的计算值和实验结果见表1，可以看出，有限元模型的固有模态计算值与实验结果吻合良好。

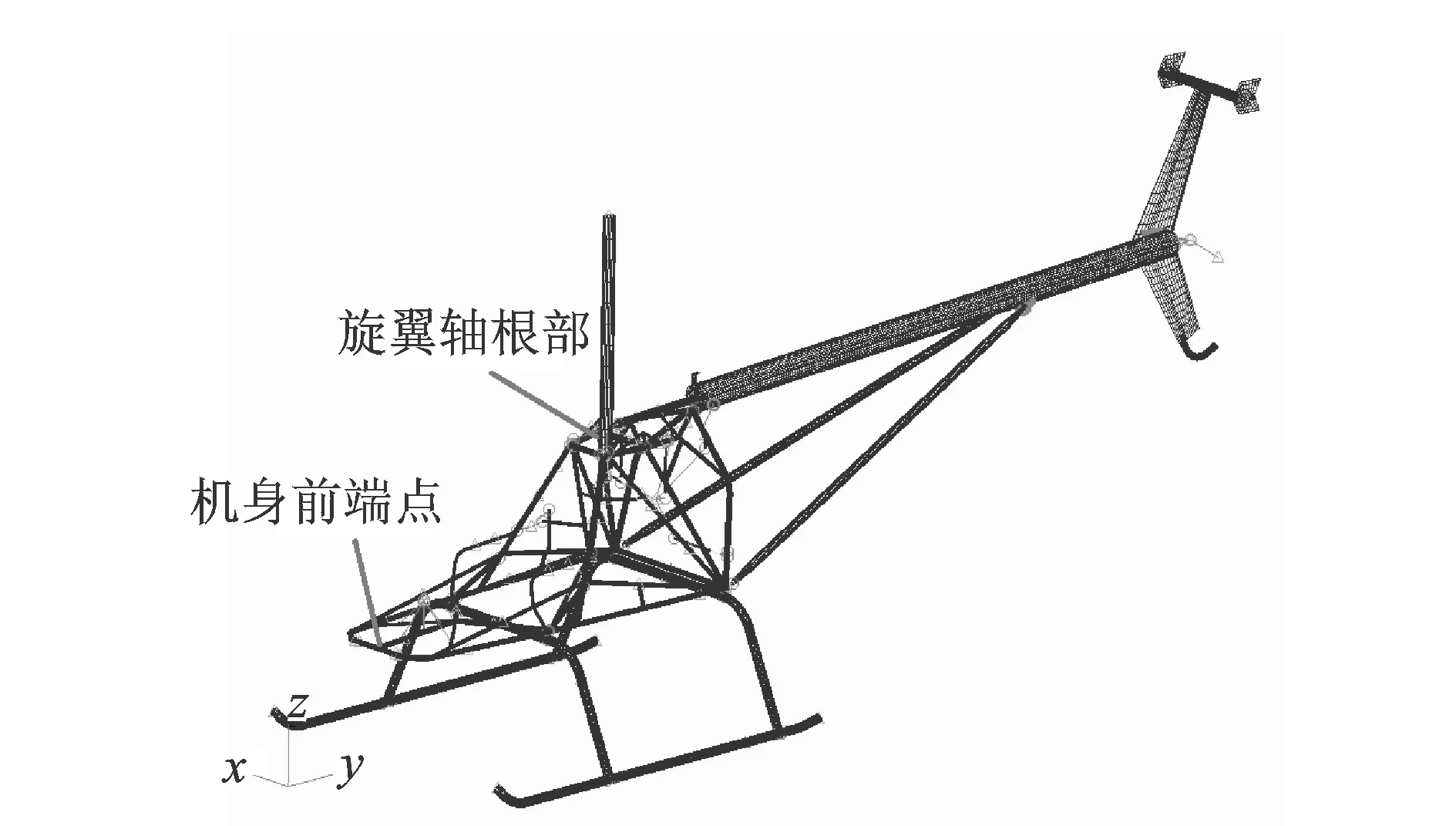
图1 机身有限元模型

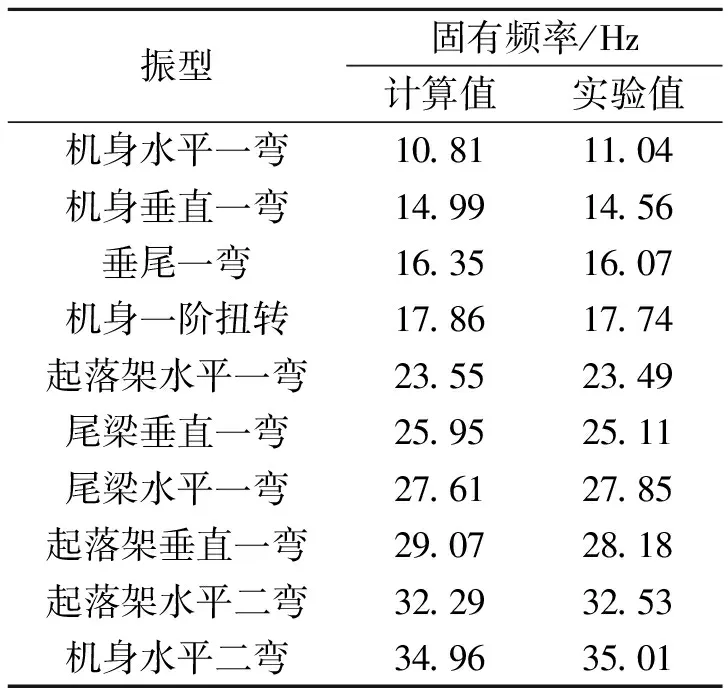
表1 机身弹性模态

为减小计算量，对桨叶运动方程和机身弹性运动方程进行了模态缩聚。为避免出现矩阵奇异，将机身刚体运动自由度分开来，放到方程右端。惯性坐标系下，得到旋翼-刚体/弹性机身耦合系统的非线性动力学方程为：

(5)

式中M，C，K为系统的质量、阻尼和刚度矩阵；FL和FNL表示线性和非线性力向量；p是模态缩聚后的广义坐标。下标b，G，r和e分别表示与桨叶、桨毂万向铰、机身刚体运动和机身弹性模态相对应的自由度。旋翼/机身耦合系统方程是一个非线性，周期系数常微分方程组，本文采用时间有限元方法进行求解。机身刚体运动则由配平方程来求解，并通过与式(5)迭代，得到耦合方程的解。

1.2 CFD分析模型

旋翼流场采用非定常Euler/N-S方程进行求解，并通过动网格与动态嵌套网格方法来实现桨叶的弹性变形和刚体运动。为节省计算时间，本文控制方程采用非定常Euler方程。计算中采用双时间步进行时间推进，每个旋转周期进行360个物理时间步的计算，每个物理时间步内进行20个伪时间步的迭代计算，对流通量采用Roe格式计算。

图2(a)是旋翼系统的嵌套网格装配示意图，其中背景网格由7个网格块组成，总网格单元数为1 749 000。单片桨叶网格如图2(b)所示，桨叶采用C-H型结构网格，由8个子网格块组成，共171 900个网格单元。两组桨叶网格和背景网格组成整个嵌套网格系统，网格总单元数为2 092 800。

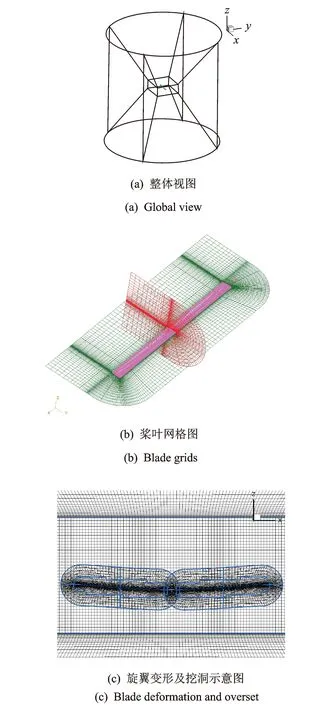
图2 旋翼系统网格图

1.3 分析流程

直升机的配平计算是旋翼气动弹性分析中不可缺少地重要环节，本文采用自由飞行条件下的6自由度平衡方程，来计算直升机的操纵输入(包括总距θ75和周期变距θ1c,θ1s)、飞行姿态角(俯仰角αs和滚转角φs)和尾桨总距θT。

旋翼-刚体/弹性机身耦合系统的响应，采用带配平的松耦合迭代方法进行求解，CFD和CSD数据每旋转一周交换一次，具体分析步骤如下：

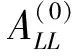
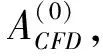
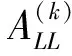
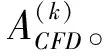
5．重复步骤3和4直到系统的响应收敛。此时机身的振动响应即为旋翼/机身耦合系统的非线性振动响应。

2 结果与讨论

本文以某两片桨叶跷跷板式直升机为算例，直升机的具体参数如表2所示。每片桨叶划分为6个具有15自由度的中等变形梁单元，各个单元的截面参数见表3。其中，li/R是无因次化的单元长度，mi/m0是无因次化的桨叶线密度，该算例中取参考线密度m0=2.63 kg/m。EIz/m0Ω2R4，EIy/m0Ω2R4和GJ/m0Ω2R4分别为无因次化的摆振、挥舞和扭转刚度。

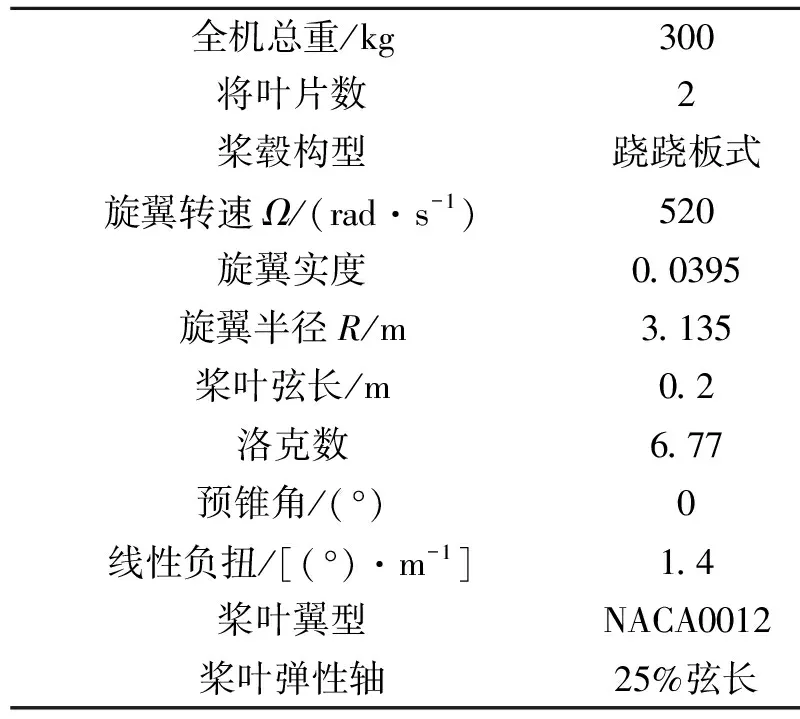
表2 直升机参数

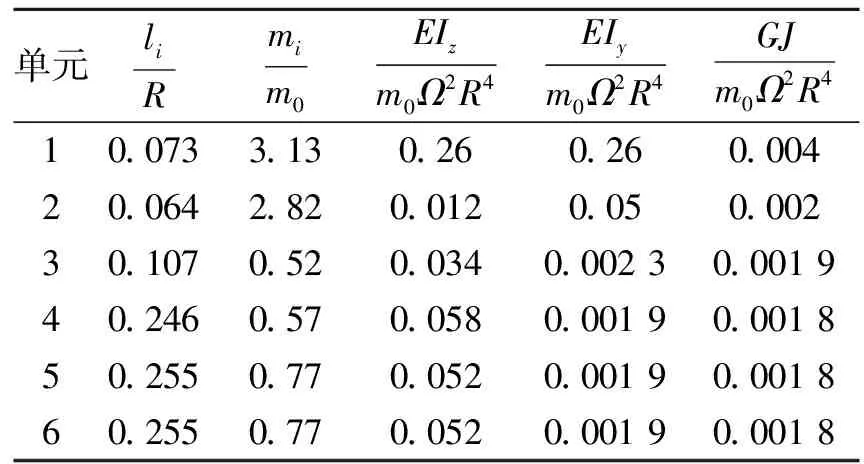
表3 桨叶单元参数

2.1 悬停状态

在悬停状态下，采用本文所提出的旋翼-刚体/弹性机身耦合系统分析方法，对旋翼轴根部和机身前端点(如图1所示)的振动响应进行分析，并将计算结果与实验值进行比较。

图3是旋翼轴根部振动加速度功率谱密度曲线的计算值和实验值的对比。可以看出，对于2倍通过频率(2/rev)和4倍通过频率(4/rev)的振动响应，计算值与实验值吻合良好。试验中有一定的通过频率响应成分，而计算中没有，这主要是由旋翼各片桨叶的气动和质量不平衡造成的，而在计算中没有考虑这些因素。此外，实验中还有较大的52～54 Hz频率响应，这是由发动机(额定转速3 200 r/min)振动造成的。旋翼轴根部靠近发动机，因此其受发动机振动的影响较大，从图3(c)中可以看出，当主旋翼所引起的响应较小时，发动机振动和噪声的影响将明显增大。

图4是机身前端点处的加速度功率谱密度曲线，由于此点远离发动机，因此其振动受发动机的影响明显减小。

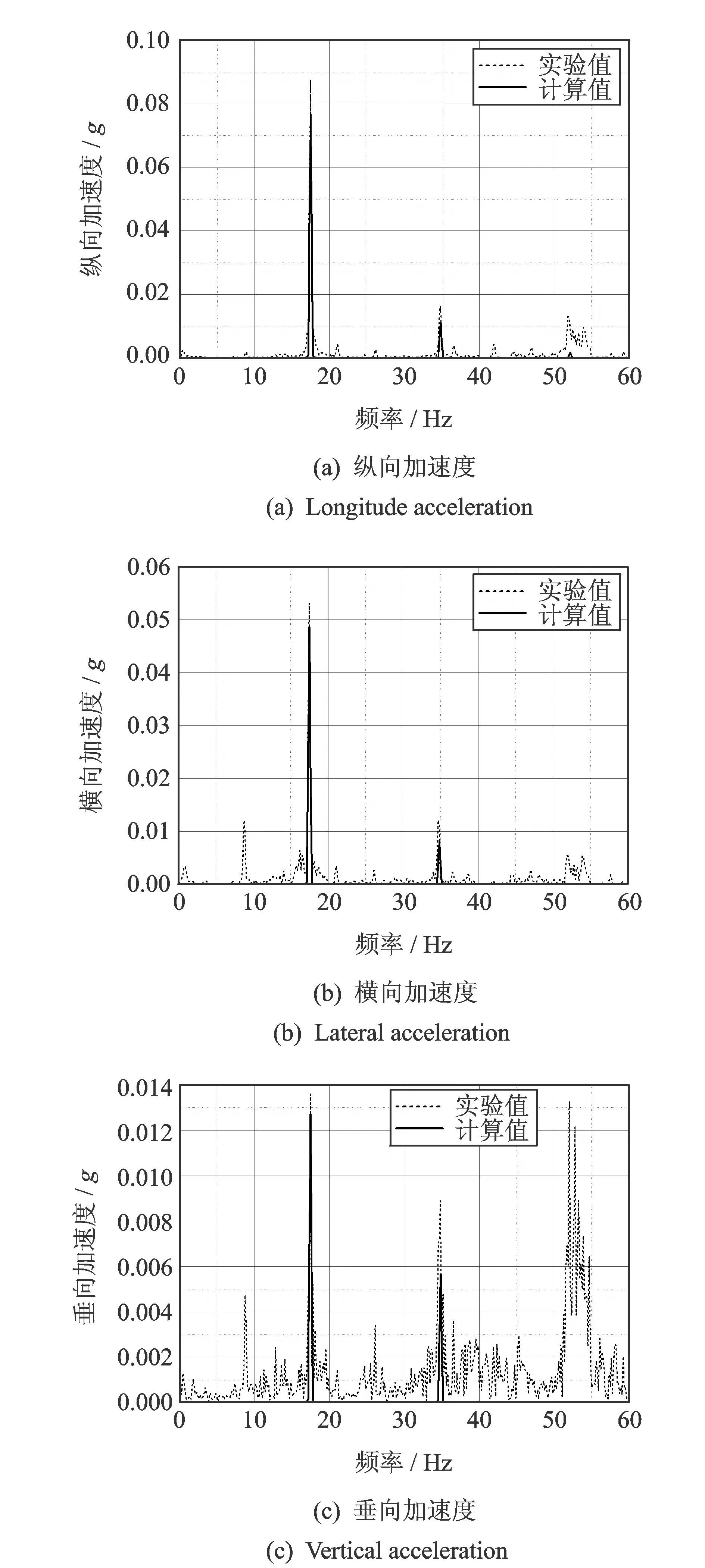
图3 旋翼轴根部振动自功率谱密度曲线

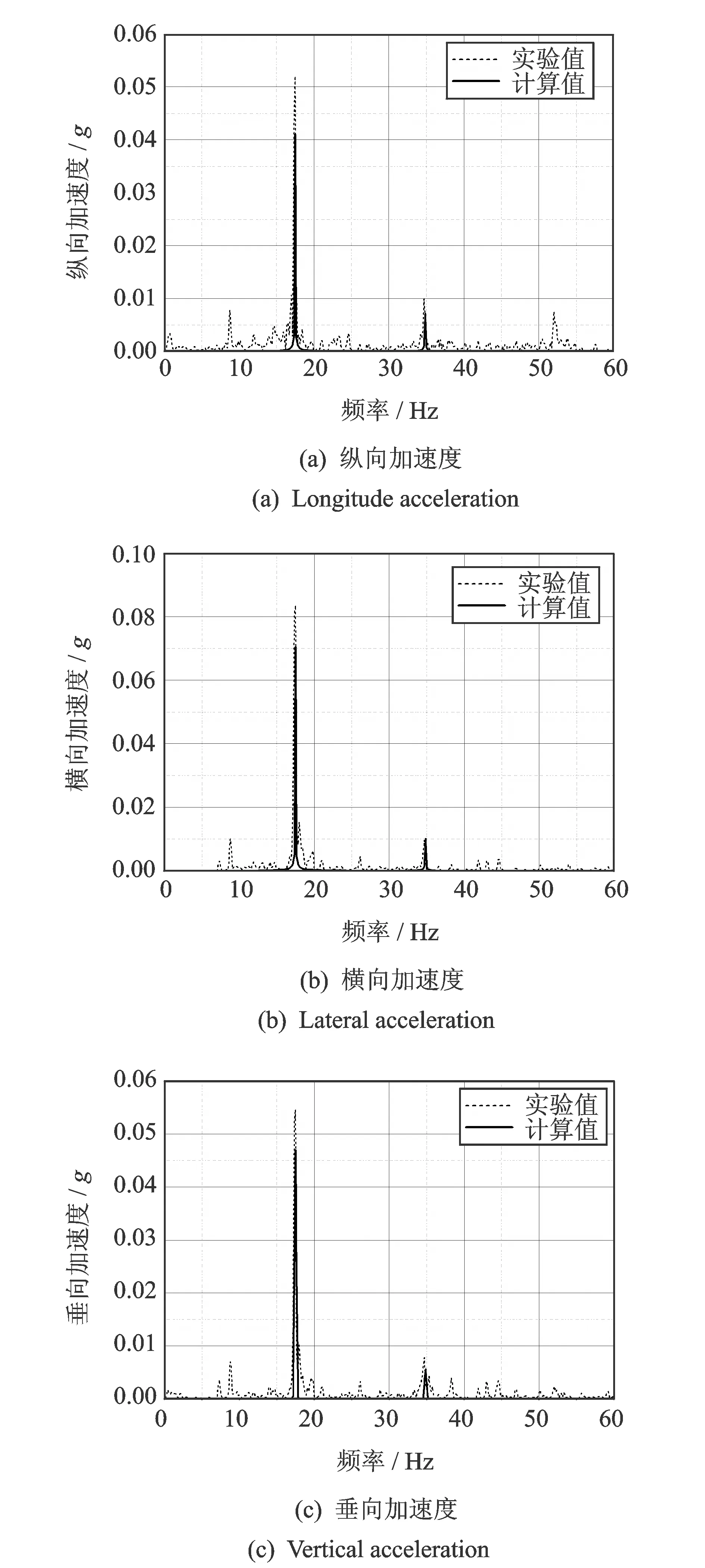
图4 机身前端点振动自功率谱密度曲线

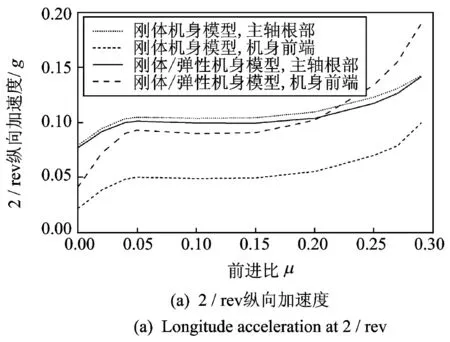
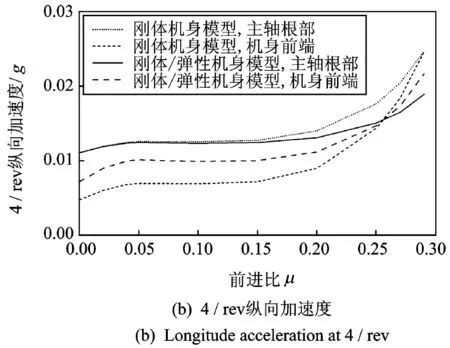
图5 机体纵向振动随前飞速度的变化

2.2 前飞状态

在定常前飞状态下，对机身前端点和旋翼轴根部的振动响应进行计算，研究前飞速度对机身振动水平的影响，并比较考虑和不考虑机身弹性运动对分析结果的影响。

图5～7是机体的纵向、横向和垂向加速度响应幅值随前飞速度的变化曲线。从图中可以看出，当直升机由悬停转入前飞状态时，机体振动水平会随着前飞速度的增加而迅速增大，并在前进比μ=0.05左右时到达一个局部峰值；当前进比μ在0.05～0.2范围内时，机体振动水平则基本保持不变；当μ>0.2后，机体的振动水平又会随着前飞速度的增加而迅速增大。

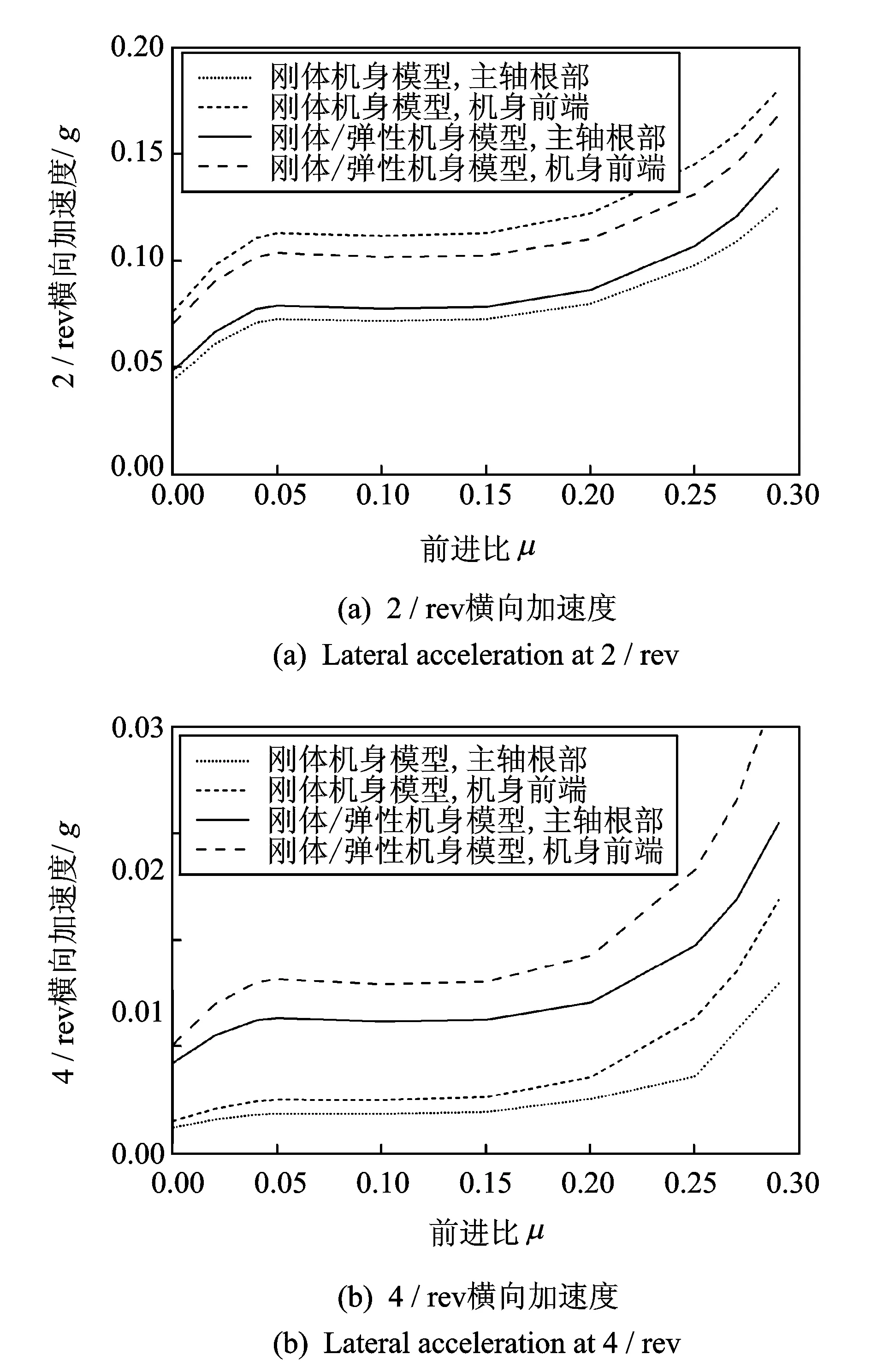
图6 机体横向振动随前飞速度的变化

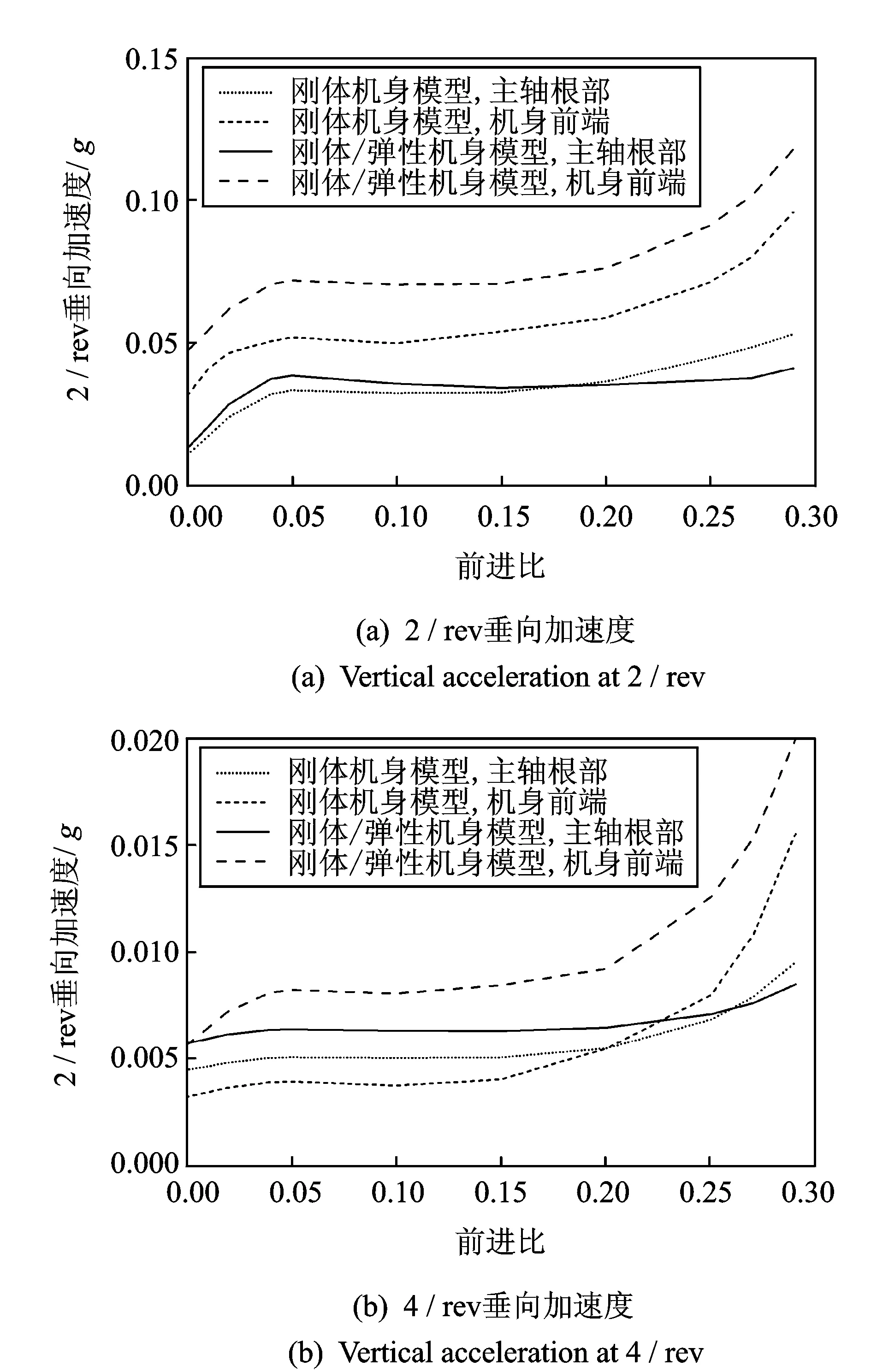
图7 机体垂向振动随前飞速度的变化

对比图5～7可以看出，机体的纵横向振动响应明显高于垂向振动响应，这说明旋翼的横向力扰动相对较大。在前进比μ<0.2时，各个自由度均以2/rev的频率响应分量为主，4/rev频率的响应相对较小。而当μ>0.2时，4/rev频率的振动响应所占比重则逐渐增大。

对比仅考虑机身刚体运动和综合考虑刚体/弹性运动两种分析模型，可以看出，对旋翼轴根部位置，两者的分析结果误差较小；而对机身前端点，两者的误差则较大。这是因为旋翼轴弹性相对较小，因此旋翼轴根部振动主要以刚体运动为主；而机身前端点远离旋翼，且结构弹性较大，因而其振动中弹性运动所占的分量比较大。由此可见，在进行直升机振动水平分析时，机身的弹性影响是不能忽略的。

3 结 论

本文提出了一种直升机旋翼-刚体/弹性机身耦合系统振动响应分析方法，综合考虑了桨叶的几何非线性，机身的弹性和刚体运动等。桨叶采用15自由度中等变形梁单元，通过基于动网格和动态嵌套网格技术的非定常Euler/N-S方程，与准定常气动力模型相结合的方法来求解弹性旋翼流场，利用CSD软件建立精细的机身三维有限元模型，最后用松耦合迭代方法对系统的响应进行分析。该方法能准确模拟机身结构动力学和旋翼流场的特性，具有很好的分析精度和工程适用性，可广泛应用于直升机振动水平分析和减振设计。

以某小型直升机为例，通过MSC/Patran软件建立精细的机身三维有限元模型，并根据模态试验对模型进行修正。计算了悬停状态下机身典型位置的振动响应，计算结果与实验值吻合良好。研究了前飞速度对机身振动水平的影响，结果表明，在小速度和大速度前飞时，机身振动水平随前飞速度的增加而增大，在中等速度段，机体振动水平基本保持不变。

分析中采用了仅考虑机身刚体运动和综合考虑刚体/弹性运动两种模型，结果表明，在旋翼轴根部，机身振动以刚体运动为主，而在机身前端处的机体振动响应中，结构弹性的影响非常大。因此，在进行直升机振动水平分析时，必须考虑机身结构弹性的影响。

参考文献：

[1] Gerstenberger W, Wood E R. Analysis of helicopter aeroelastic characteristics in high speed flight[J]. AIAA Journal, 1963, 1(10): 2 366—2 381.

[2] Staley J A, Sciarra J J. Coupled rotor/airframe vibration prediction methods[R]. NASA SP-352, 1974, 81—90.

[3] Hsu T K, Peters D A. Coupled rotor/airframe vibration analysis by a combined harmonic-balance impedance-matching method [J]. Journal of the American Helicopter Society, 1982, 27(1): 25—34.

[4] Warmbrodt Friedmann. Formulation of coupled rotor/fuselage equations of motion [J]. Vertica, 1979, 3: 245—271.

[5] Fledel. Coupled rotor/airframe vibration analysis[D]. Aerospace Engineering, University of Maryland, 1989.

[6] Thiem Chiu, Peretz P Friedmann. A coupled helicopter rotor/fuselage aeroelastic response model for ACSR[A]. AIAA Conference[C]. New Orleans,USA.1995, 574—600.

[7] Richard C Cribbs, Peretz P Friedmann, Thiem Chiu. Coupled helicopter rotor/flexible fuselage aeroelastic model for control of structural response[J]. AIAA Journal, 2000, 38(10):1 777—1 788.

[8] Senthilvel Vellaichamy, Inderjit Chopra. Aeroelastic response of helicopters with flexible fuselage modeling[A]. AIAA Conference[C]. Dallas,USA.1992： 2 015—2 026.

[9] Hyeonsoo Yeo, Inderjit Chopra. Coupled rotor/fuselage vibration analysis for teetering rotor and test data comparison[J]. Journal of Aircraft, 2001, 38(1):111—121.

[10] Klausdieter Pahlke, Berend G， van der Wall. Chimera simulations of multibladed rotors in high-speed forward flight with weak fluid-structure-coupling [J]. Aerospace Science and Technology, 2005, 9: 379—389.

[11] Mark Potsdam, Hyeonsoo Yeo, Wayne Johnson. Rotor airloads prediction using loose aerodynamic/structural coupling [J]. Journal of Aircraft, 2006，43(3)：732—742.

[12] Jasim Ahmad, Robert T Biedron. Code-to-code comparison of CFD/CSD simulation for a helicopter rotor in forward flight[A]. AIAA Applied Aerodynamics Conference[C]. Honolulu, USA. 2011.