形态分量分析在转子早期碰摩故障诊断中的应用
陈向民, 于德介, 李 星, 李 蓉
(湖南大学汽车车身先进设计制造国家重点实验室,湖南 长沙 410082)
引 言
转子碰摩是转子系统中经常发生的主要故障之一,轻则引起机器的异常振动、磨损,重则导致断轴等恶性事故,带来巨大的经济损失甚至人员伤亡[1]。因此,对转子早期碰摩故障进行研究具有重要的实际意义。
目前围绕转子碰摩故障的研究主要包括两个方面:碰摩故障的非线性动力学特性分析和碰摩故障的故障诊断方法研究[2,3]。对于碰摩故障诊断方法,目前主要有共振解调、小波变换、经验模态分解 (Empirical mode decomposition,EMD)等方法[4~10],并取得了一定的成果。
在转子早期单点碰摩故障中,碰撞表现出很强的周期性,并引发出系统的冲击响应,导致故障信号中出现周期性冲击成分。但由于处于碰摩的早期,故障振动信号中的冲击成分微弱,容易被工频及其谐波淹没,不易察觉。而重要的故障信息往往包含在冲击成分中,因此,如能从碰摩故障振动信号中有效地提取出冲击成分,并识别其周期,则可对碰摩故障的诊断提供重要的依据[11]。
最近,Starck等基于信号的稀疏表示和形态多样性提出了形态分量分析(Morphological component analysis,MCA)[12],并在此基础上发展了其扩展算法广义形态分量分析(Generalized morphological component analysis,GMCA)。形态分量分析的主要思想是利用信号组成成分的形态差异性(可以由不同的字典稀疏表示)进行分离[13],该方法首先应用于图像处理和脑信号分离中[14~16],近来,GMCA方法被引入机械故障诊断领域,并用于齿轮箱复合故障诊断中[17,18],取得了较好的效果,但GMCA方法需要同时采集多路传感器信号,在一定情况下会增加工程应用难度。MCA方法能从单路传感器信号中分离出不同形态的信号分量,工程上应用较为简便,因此本文将MCA方法引入故障振动信号分析。
在MCA算法中采用了软阈值方法对小波系数进行阈值去噪处理,由于软阈值方法在去噪的同时也削弱了信号,效果不佳。Bobin等提出了一种 最大平均(Mean of Max,MOM)机制对MCA的算法性能进行了改善[19],并采用硬阈值方法对小波系数进行阈值去噪。其研究表明,采用硬阈值法比软阈值法有更好的分离效果。但由于硬阈值方法在阈值点是不连续的,会对重构信号带来较大的方差。
Gao等针对软阈值方法和硬阈值方法的不足[20],在对小波系数阈值去噪的研究中提出了一种折中的阈值去噪方法,即半软阈值方法。研究表明,半软阈值方法在阈值去噪方面比软阈值方法和硬阈值方法更具优势。因而,本文将半软阈值方法引入MCA方法中,用于小波系数的阈值消噪处理。
本文将形态分量分析引入转子早期碰摩故障诊断中,并对其阈值去噪进行了改进,提出了基于半软阈值的形态分量分析的转子早期碰摩故障诊断方法。当转子发生早期碰摩故障时,其振动信号中往往会出现周期性的冲击成分,但由于处于碰摩故障的早期,冲击成分微弱,容易淹没在工频及谐波信号中,不易察觉。形态分量分析根据信号中周期成分与冲击成分形态的差异,采用不同的过完备字典分别进行稀疏表示(每种成分能且仅能用一种字典进行稀疏表示),实现信号中工频及其谐波成分与冲击成分的分离,并通过对冲击成分周期的识别诊断转子早期碰摩故障。算法仿真和应用实例表明了该方法的有效性。
1 形态分量分析方法简介
1.1 形态分量分析原理
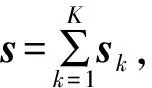
(1)
由于式(1)为非凸函数,难于求解,且算法复杂度随着字典列数的增加指数上升。因此,根据基追踪算法,可将式(1)中的0范数转化为1范数,此时,可将式(1)转化为可优化求解的线性规划形式
(2)
放宽式(2)的约束条件,可将式(2)转换为
(3)
式中λ为给定的阈值。
根据sk=Φkαk,给定sk,便可以得到αk
(4)
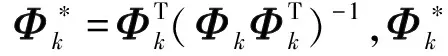
根据式(3)和式(4),从而可将式(1)中系数{α1,…,αK}的优化求解问题转化为式(5)中信号分量{s1,…,sK}的优化求解问题
(5)
1.2 阈值函数的选择
对于式(5)的优化求解问题,Starck等在块协调松弛(Block-Coordinate-Relaxation,BCR)算法的基础上[12],给出了MCA的数值实现步骤。在这一算法步骤中,变换系数αk的阈值去噪采用了软阈值方法
(6)
式中 sgn(·)为符号函数。但由于软阈值方法在保证信号连续性的同时,却削弱了有用信号,故效果不佳。Bobin等提出了一种MOM机制对MCA的算法性能进行了改善[19],并在变换系数αk的阈值去噪处理上采用了硬阈值方法
(7)
然而,由于硬阈值法在阈值点不连续,会给信号带来较大的方差。
针对软阈值处理和硬阈值处理的不足,Gao等提出了半软阈值法[20]
(8)
式中δk2为上阈值,δk1为下阈值,一般δk2=2δk1。
半软阈值法是软阈值法和硬阈值法的一种折中形式,能更有效地降低均方差,同时抑制噪声,较好地解决了抑制噪声与保留信号细节之间的权衡问题。因此,本文采用半软阈值方法对变换系数αk进行消噪处理。
2 基于形态分量分析的转子碰摩故障诊断原理
当转子系统中出现动静碰摩故障时,由于转子与定子的周期性碰撞,其故障振动信号中往往伴有周期性冲击成分,该周期性冲击成分包含了碰摩故障的重要信息。但在早期碰摩故障中,冲击成分微弱,常淹没在转子工频及其谐波成分中,不易察觉。因此,如能从转子碰摩故障信号中提取出周期性冲击成分,并识别其周期,将为转子碰摩故障的诊断提供重要的依据。
由于转子早期碰摩故障振动信号往往由以转频及其谐波为主要成分的周期成分、包含转子早期碰摩故障信息的冲击成分及随机噪声组成。周期成分表现为信号的光滑部分,而冲击成分表现为信号的细节部分,因此,可根据周期成分与冲击成分的形态差异,利用MCA方法对转子早期碰摩故障信号进行分析,实现周期成分与冲击成分的分离,再对冲击成分中的冲击周期进行识别即可诊断转子早期碰摩故障。基于形态分量分析的转子早期碰摩故障诊断步骤如下:
1) 构建局部离散余弦变换与离散正弦变换字典用于稀疏表示转子工频及其谐波,构建8阶消失矩Symlet小波字典用以稀疏表示信号中的冲击成分[17];迭代次数的大小会影响算法的计算量和精度,下文中迭代次数取100;MCA方法提供了两种阈值选择方式,一种是用户自己自定义输入阈值;另一种为根据信号自适应确定阈值,但需选定停止准则参数stop的值,下文中stop值取3;
2) 利用基于半软阈值的MCA方法对转子碰摩故障信号进行分析,得到包含转子工频及其谐波的正弦成分、包含转子碰摩故障信息的冲击成分以及两成分之和与原始转子信号的差值,即噪声信号;
3) 对包含转子碰摩故障信息的冲击成分进行分析,根据冲击出现的周期即可诊断转子早期碰摩故障。
3 算法仿真
为验证形态分量分析对正弦信号和冲击信号的分离效果,设置下式所示仿真信号
x(t)=h(t)+s(t)+n(t)
(9)
式中n(t)为噪声成分,以模拟随机干扰;h(t)表示正弦成分,由K个幅值为Ai、频率为fi的正弦成分构成,其表达式如下式所示
(10)
s(t)表示周期冲击成分[23],由M个幅值为Bm、衰减系数为β、共振频率为fr的单冲击信号构成,冲击之间的时间间隔为Tp,其表达式如下式所示
cos[2πfr×(t-mTp)]u(t-mTp)
(11)
式中u(t)为单位阶跃函数。
取采样频率为1 024 Hz,采样点数为512点,将表1中各参数值代入式(10)和(11)中,得到的正弦分量和冲击分量分别如图1(a)和图1(b)所示。将式(10)和(11)代入式(9),并加入幅值为0.3的随机噪声(如图1(c)),得到的仿真合成信号如图1(d)所示。从图1(d) 中可知,冲击分量已淹没在信号中。
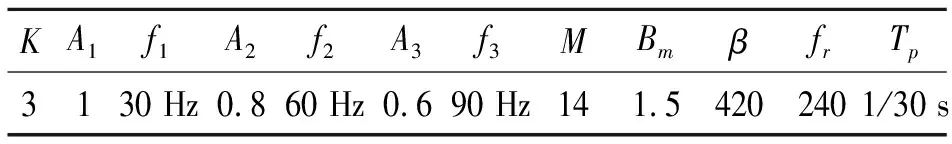
表1 仿真信号的各参数值
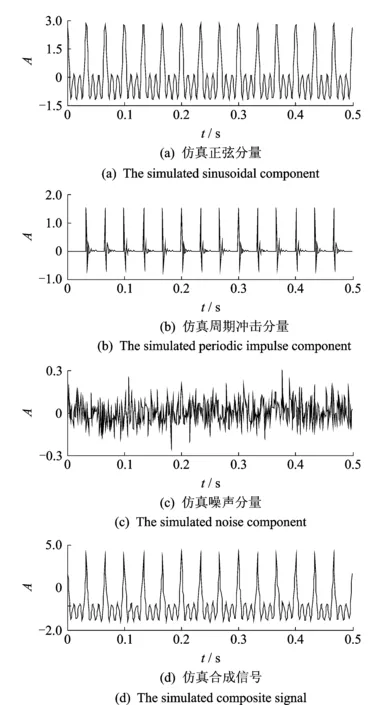
图1 仿真信号
利用基于半软阈值的形态分量分析对图1(d)所示仿真合成信号进行分析,得到的结果如图2所示。对比图1可知,正弦分量与冲击分量已基本分离,仅在信号幅值方面略有差异。
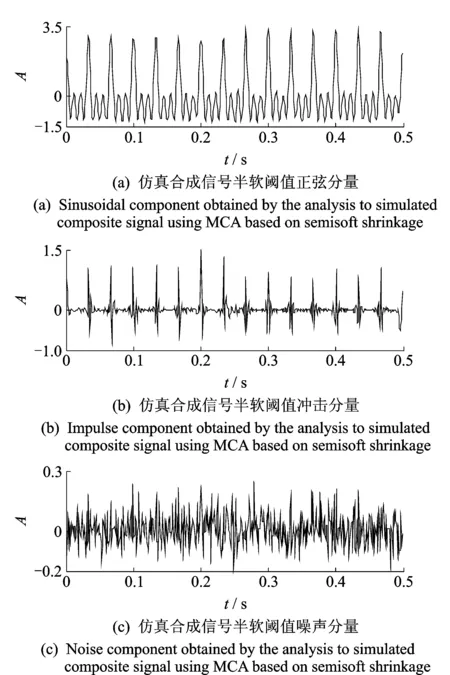
图2 基于半软阈值的仿真合成信号形态分量分析
利用基于硬阈值的形态分量分析对图1(d)所示仿真合成信号进行分析,得到的分解结果如图3所示。对比图1可知,信号中的正弦分量已被较好地分离出来,冲击成分的周期也依稀可见,但幅值存在较大的差异,且在噪声分量中存在较多的冲击。对比与图2,3的分离效果要远逊色于图2。
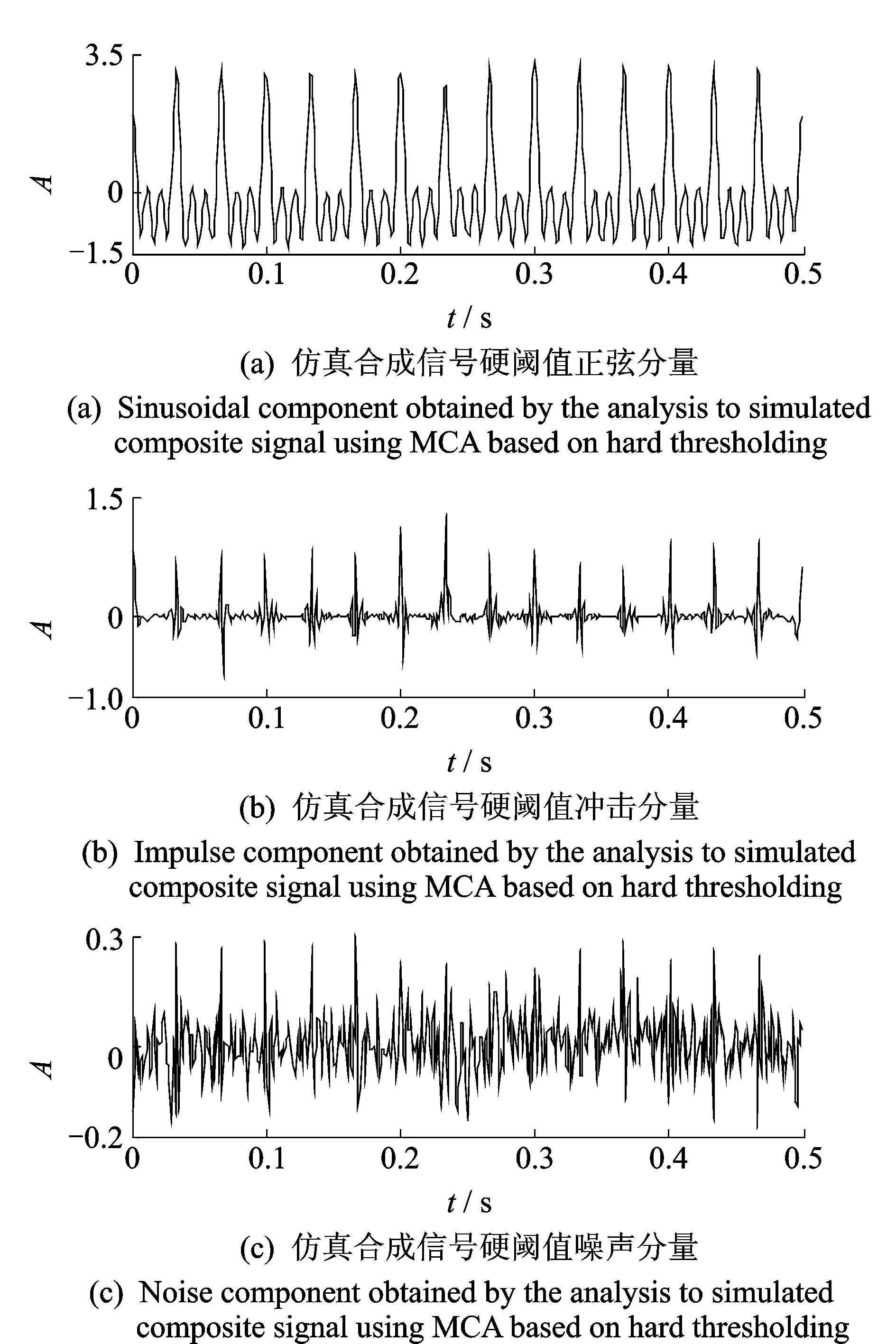
图3 基于硬阈值的仿真合成信号形态分量分析
4 应用实例
为验证基于半软阈值的MCA方法从转子早期碰摩故障信号中提取冲击成分的有效性,进行了转子单点碰摩实验。转子碰摩实验装置结构示意图如图4所示。图中采用一个可调间隙的轴承(部件8)来实现碰摩故障的模拟实验。
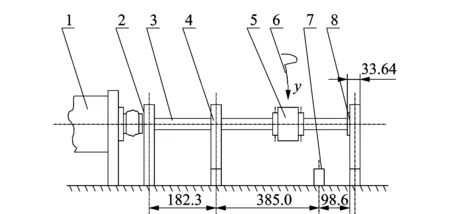
1.电机; 2.轴承1; 3.轴(Φ10); 4.轴承2;5.圆盘; 6.电涡流位移传感器(测垂直方向);7.尺寸定位块; 8.可调间隙轴承
实验中采用电涡流位移传感器拾取位移信号,转轴工频为3 000 r/min,采样频率为6 400 Hz,采样点数为1 024。拾取的转子动静碰摩位移信号如图5所示。
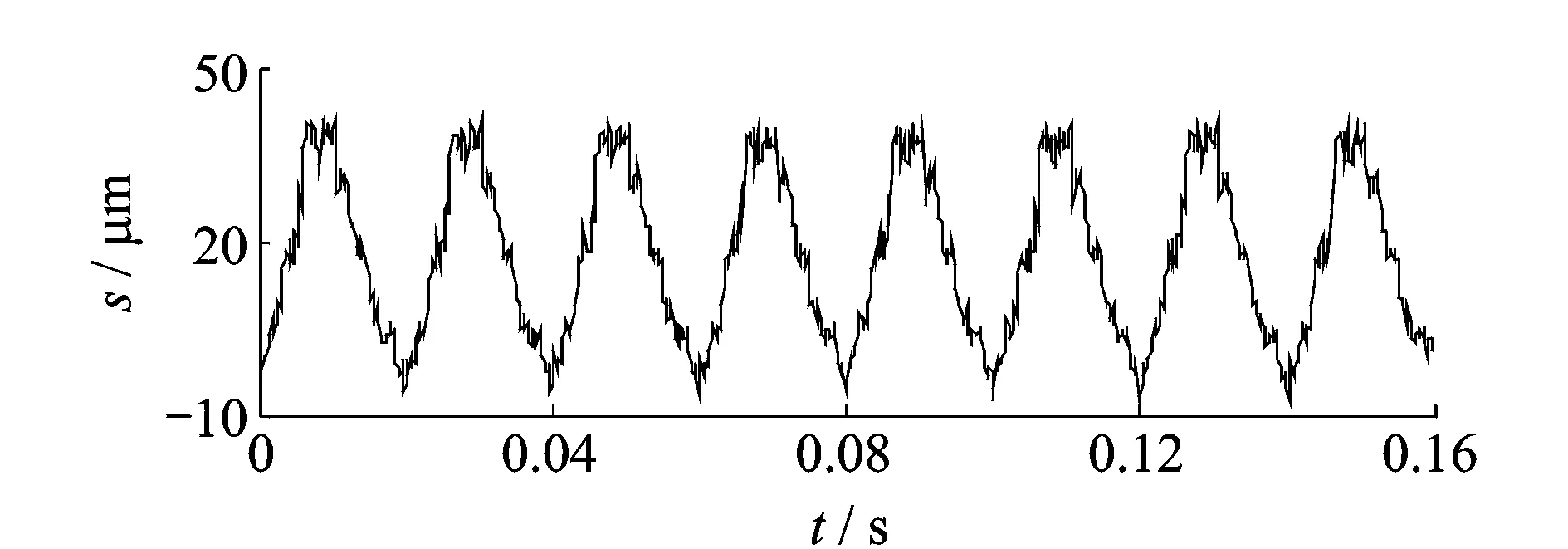
图5 转子碰摩原始信号
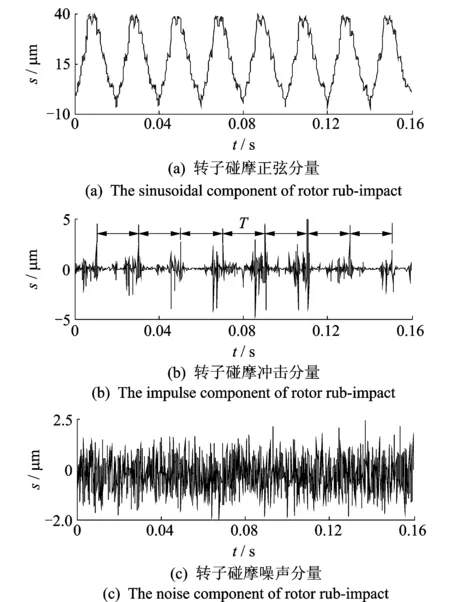
图6 基于半软阈值的转子碰摩信号形态分量分析
利用基于半软阈值的MCA方法对图5转子碰摩原始信号进行分析,得到的各分量如图6所示。图6(a)主要由工频及其谐波分量构成,由于去除了噪声和冲击成分,信号较图5光滑。图6(b)为分离出的冲击分量,图中存在周期性冲击现象,冲击之间的时间间隔T≈0.02 s,即冲击出现的频率为50 Hz,说明转子每转一圈产生一个冲击,与转子单点碰摩故障相符,验证了方法的有效性。
同时,采用db8小波对图5所示转子早期碰摩信号进行4层小波分解,图7为分解得到的第一层细节分量的时域波形图,图中也可依稀辨别冲击的周期性,但其中包含了较多的噪声成分,冲击效果要逊色于图6(b)。
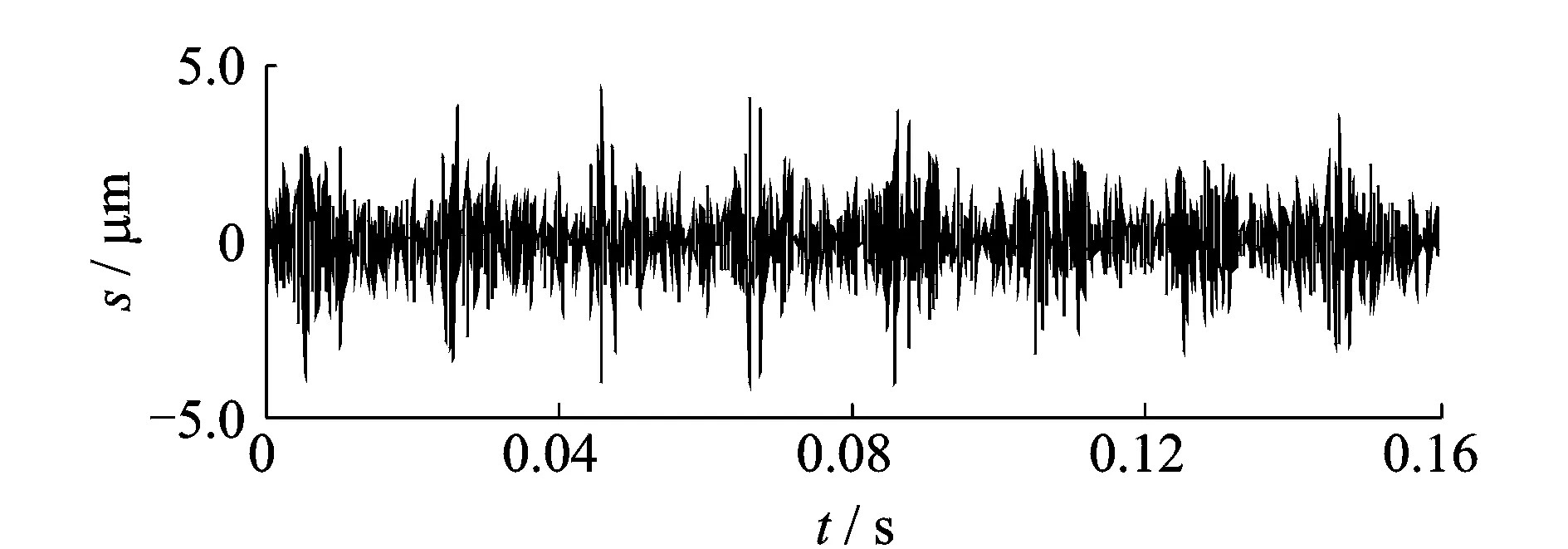
图7 基于db8小波分解的第一层细节分量
5 结 论
本文将形态分量分析引入转子早期碰摩故障诊断,提出了基于半软阈值的形态分量分析的转子早期碰摩故障诊断方法,主要研究结论如下:
1) 算法仿真结果表明,在分离效果上,基于半软阈值的MCA方法要明显优于基于硬阈值的MCA方法。
2) 应用实例表明,基于半软阈值的MCA方法应用于转子早期碰摩故障诊断,能有效地分离出淹没在信号中的冲击成分,从而能根据冲击成分的冲击周期进行转子早期碰摩故障诊断。
3) 本文将形态分量分析用于单通道信号的成分分离,取得了一些效果,但还有很多地方尚需进一步研究,如字典的自适应优化选择、强背景噪声环境下的形态成分分离等。
参考文献:
[1] 罗洁思,于德介. 基于MCSSD的转子碰摩故障早期检测[J]. 振动工程学报,2010,23(2):221—224.Luo Jiesi,Yu Dejie. Early detecting the rub-impact fault in rotors based on MCSSD method[J]. Journal of Vibration Engineering,2010,23(2):221—224.
[2] 刘耀宗,胡茑庆. Jeffcott转子碰摩故障试验研究[J]. 振动工程学报,2001,14(1):96—99.Liu Yaozong,Hu Niaoqing. Some observations of rub-impact fault on Jeffcott rotor[J]. Journal of Vibration Engineering,2001,14(1):96—99.
[3] 杨树华,郑铁生,张文. 油膜支承转子碰摩动力学行为研究[J]. 振动工程学报,2004,17(S):34—36.Yang Shuhua,Zheng Tiesheng,Zhang Wen. Study on dynamic behavior of rub-impact rotor system supported by oil film bearings[J]. Journal of Vibration Engineering,2004,17(S):34—36.
[4] 孙云岭,张永祥,常汉宝. 基于定子振动的转子碰摩故障诊断方法研究[J]. 振动工程学报,2009,22(4):391—394.SUN Yunling,ZHANG Yongxiang,CHANG Hanbao. Method of rotor rub-impact faults diagnosis based on stator vibration signal[J]. Journal of Vibration Engineering,2009,22(4):391—394.
[5] 王善永,陆颂元,马元奎,等. 汽轮发电机组转子动静碰摩故障检测的小波分析方法研究[J]. 中国电机工程学报,1999,19(3):1—5.WANG Shanyong,LU Songyuan,Ma Yuankui,et al. Application of wavelets to turbo generator unit for impact fault detection[J]. Proceedings of the CSEE,1999,19(3):1—5.
[6] 彭志科,何永勇,卢青,等. 用小波时频分析方法研究发电机碰摩故障特征[J]. 中国电机工程学报,2003,23(5):75—79.PENG Zhike,HE Yongyong,LU Qing,et al. Using wavelet method to analyze fault features of rub rotor in generator[J]. Proceedings of the CSEE,2003,23(5):75—79.
[7] 宋友,柳重堪,李其汉. 基于小波变换的转子动静件碰摩故障诊断研究[J]. 振动工程学报,2002,15(2):319—322.SONG You,LIU Zhongkan, LI Qihan. Research on rub-impact fault between rotor and stator using wavelet transform[J]. Journal of Vibration Engineering,2002,15(2):319—322.
[8] 王学军,马辉,孙伟,等. 基于小波分析的转子碰摩故障特征提取[J]. 农业机械学报,2008,39(4):147—151.Wang Xuejun,Ma Hui,Sun Wei,et al. Feature extraction of rotor fault based on wavelet analysis[J]. Transaction of the Chinese Society for Agricultural Machinery,2008,39(4):147—151.
[9] 何田,刘献栋,单颖春,等. 改进Hilbert-Huang变换及其在转静子碰摩仿真中的应用[J]. 航空动力学报,2007,22(10):1 779—1 784.He Tian,Liu Xiandong,Shan Yingchun,et al. Improved Hilbert-Huang transform and its application in rotor stator rub[J]. Journal of Aerospace Power,2007,22(10):1 779—1 784.
[10] Cheng Junsheng,Yu Dejie,Tang Jiashi, et al. Local rub-impact diagnosis of the rotor systems based on EMD[J]. Mechanism and Machine Theory,2009,44(4):784—791.
[11] 李允公,刘杰,张金萍. 基于实测冲击响应的转子碰摩故障特征提取方法[J]. 机械工程学报,2007,43(4):224—228.Li Yungong,Liu Jie,Zhang Jinping. Signature extracting method of the fault of rubbing rotor based on measured impulse response[J]. Chinese Journal of Mechanical Engineering,2007,43(4):224—228.
[12] Starck J L,Moudden Y,Robin J. Morphological component analysis[J]. Proceedings of SPIE,2005,59(14):1—15.
[13] 李映,张艳宁,许星. 基于信号稀疏表示的形态成分分析:进展和展望[J]. 电子学报,2009,37(1):146—152.Li Ying,Zhang Yanning,Xu Xing. Advances and perspective on morphological component analysis based on sparse representation[J]. Acta Electronica Sinica,2009,37(1):146—152.
[14] Starck J L,Elad M,Donoho D. Redundant multiscale transforms and their application for morphological component separation[J]. Advances in Imaging and Electron Physics,2004,132(82):287—384.
[15] Elad M,Starck J L,Querre P. Simultaneous cartoon and texture image inpainting using morphological component analysis(MCA)[J]. Journal on Applied and Computational Harmonic Analysis ACHA,2005,19(3):340—358.
[16] Yong X Y,Ward R K,Birch G E. Generalized morphological component analysis for EEG source separaton and artifact removal[A]. Proceeedings of the 4th International IEEE EMBS Conference on Neural Engineering Antalya[C]. Turkey,2009:343—347.
[17] 杨杰,郑海起,关贞珍,等. 基于形态成分分析的轴承复合故障诊断[J]. 轴承,2011,(8):38—42.Yang Jie,Zheng Haiqi,Guan Zhenzhen,et al. Compound fault diagnosis for bearings based on morphological component annlysis[J]. Bearing,2011,(8):38—42.
[18] 李辉,郑海起,唐力伟. 基于改进形态分量分析的齿轮箱轴承多故障诊断研究[J]. 振动与冲击,2012,31(12):135—140.Li Hui,Zheng Haiqi,Tang Liwei. Bearing multi-fault diagnosis based on improved morphological component analysis[J]. Journal of Vibration and Shock,2012,31(12):135—140.
[19] Bobin J,Starck J L,Fadili J. Morphological component analysis:an adaptive thresholding strategy[J]. IEEE Transaction on Image Processing,2007,16(11):2 675—2 681.
[20] Gao Hongye,Bruce A G. Waveshrink and semisoft shrinkage[J]. StaSci Research Report,1995,39:5—8.
[21] Chen S S,Donoho D L,Saunders M A. Atomic decomposition by basis pursuit[J]. SIAM J. Sci. Comput.,1998,20(1):33—61.
[22] Mallet S G,Zhang Z F. Matching pursuit with time-frequency dictionaries[J]. IEEE Transaction on Signal Processing,1993,41(12):3 397—3 415.
[23] Liang M,Bozchalooi I S. An energy operator approach to joint application of amplitude and frequency- demodulations for bearing fault detection[J]. Mechanical Systems and Signal Processing,2010,24(5):1 473—1 494.

