移动荷载列作用下简支梁振动响应参数研究
王昆鹏, 夏 禾, 郭薇薇, 曹艳梅
(北京交通大学土木建筑工程学院, 北京 100044)
引 言
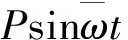
1 分析模型
1.1 问题描述
假定简支梁为等截面(EI为常数),恒载质量均
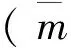
δ(x-Vt)P(t)
(1)
式中y(x,t)为梁体的竖向位移;δ为Dirac函数。
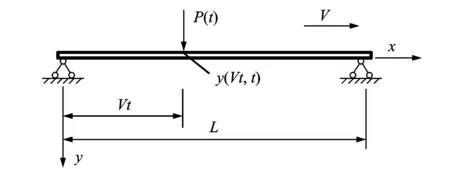
图1 移动集中力作用下的简支梁模型
1.2 问题求解
式(1)可以采用振型叠加法进行求解。对于一维的连续体,有变换表达式
(2)
式中qi(t)为振型的广义坐标,φi(x)为结构振型,对理想简支梁有φi(x)=sin(iπx/L)[4]。
将式(2)带入式(1),同时式(1)两边都乘上φn(x)并沿梁长进行积分,利用振型的正交性,整理可以得到第n阶振型的广义坐标qn(t)的运动方程
(3)
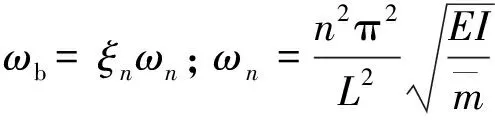
通过Duhamel积分方法求解式(3),在低阻尼及临界阻尼情况下,第n阶振型广义坐标qn(t)的特解为
(4)
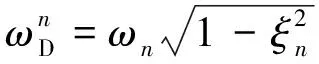
根据求得的广义坐标qn(t),利用振型叠加法得到移动荷载作用下简支梁振动位移特解的表达式
(5)
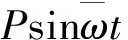
为了便于讨论各种因素对桥梁振动响应的影响,现引入2个无量纲参数α,β,以分别考虑荷载移动速度及桥梁阻尼的影响
(6)
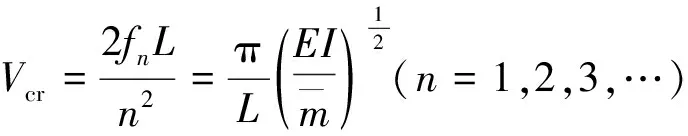
2 特殊情况求解及讨论
2.1 P(t)为移动恒定荷载 (P(t)=P)
当荷载P(t)为移动恒定荷载P时,利用三角函数积化和差公式和分部积分方法求解式(4)得到qn(t)的精确解,再利用振型叠加法得到移动荷载P作用下简支梁振动位移特解的表达式,整理得到
{n2(n2-α2)sinnωt-
(7)
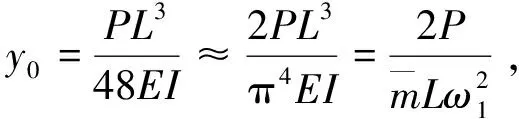
式(7)是单个移动荷载时的桥梁响应。一般将列车荷载简化为N个等间距为车辆全长lv的移动集中力荷载列,见图2。由于假定梁体变形为小变形,此时移动荷载列作用下梁体振动位移特解可表示为
(8)
式中yi(x,t)通过式(7)进行计算。
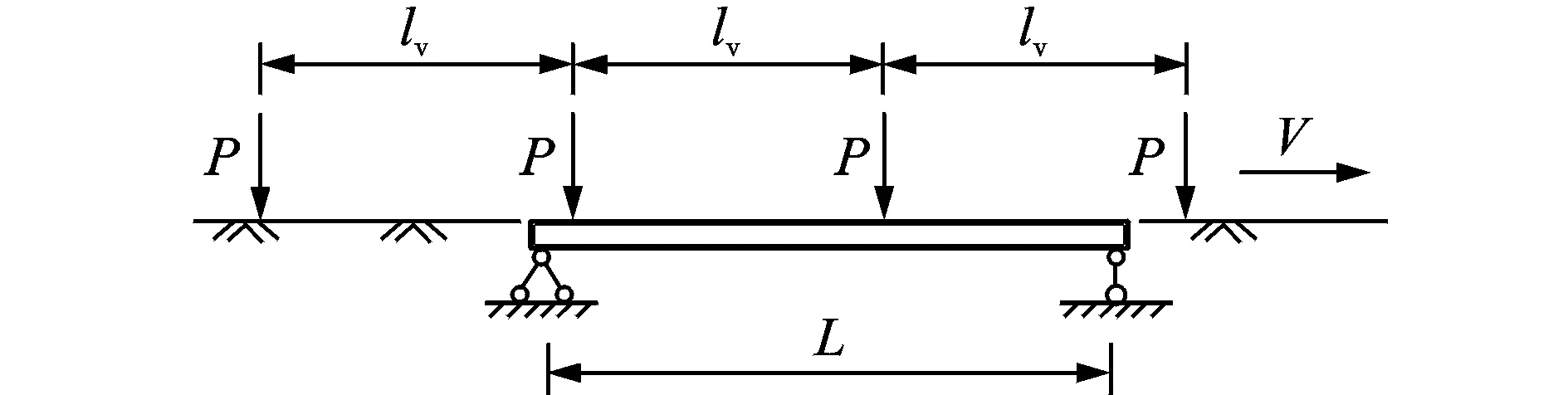
图2 通过桥跨的车辆荷载列
根据式(7)再详细地讨论几种特殊情况:
2.1.1 无阻尼情况及消振、共振分析(β=0)
a)α不为整数,β=0
如果让β=0,则式(7)可化为
(9)
实际工程中,一般有α≪1,根据式(10)可知此时梁体第一阶振型对位移的贡献最大。因此,在求解动力作用下梁体的位移响应时,仅使用第一阶振型即可以达到很高的求解精度[5]。
对式(9)中括号内的部分进行分析,如果令此项在荷载出桥时刻为零(t=L/V),则有
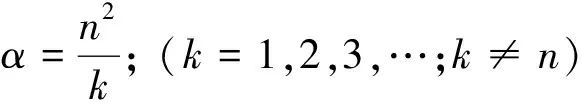
(10)
通过式(10)可以发现,当α=n2/k的时候,梁体第n阶振型的位移分量会在荷载出桥时刻归零,本文称式(10)中的速度VD= 2n2f1L/k为消振速度。在实际工程中,第一阶振型的位移分量占梁体位移的大部分,如果令n=1,此时梁体的位移会在荷载出桥时刻趋近于零。
荷载出桥以后(t>L/V),梁体处于自由振动状态,此时梁体的运动方程为
yn(x,L/V)cosωnt]
(11)
式中yn(x,L/V)=
当荷载以消振速度VD出桥时,梁体的速度却不一定为零。荷载出桥时,梁体的振动速度如下所示
(12)
从式(12)中可以看出,当n,k同奇偶时,式(12)等于零,即荷载出桥时刻,梁体第n阶振型的位移分量与速度分量同时为零;当n,k非同奇偶时,荷载出桥时刻仅有梁体第n阶振型的位移分量为零,因此在荷载出桥以后梁体第n阶振型对桥梁的后续振动依然有贡献。对于式(10)中给出的速度VD=2n2f1L/k,当n,k奇偶性相同时定义为全消振速度;当n,k奇偶性不同时定义为位移消振速度。
在线弹性阶段,梁体的位移等于各个荷载产生位移的线性叠加,当荷载列以全消振速度移动时,即α=1/k(k为奇数),梁体的动力响应会在荷载列移出梁体以后趋近于零。
b)α为整数,β=0
如果让α=k,β=0,此时式(7)的第n=k项为0/0型表达式,通过对该项求极限,可以得到简支梁振动位移特解的表达式
(13)
根据式(13)可以发现,当α=k,β=0时,梁体上任意点x处的位移是随着时间t的增大而增大的,并在t=L/V时位移达到最大值,但不会达到无穷大。这种情况相当于移动荷载P与桥梁发生了共振,说明不但移动荷载列以某个特殊速度通过桥梁时会引起桥梁共振[1,2],单个移动荷载以特殊的速度通过桥梁时也会使桥梁产生共振。
当k=n时,即荷载的加载频率是第一阶自振频率的n倍,有sin(nπVt/L)=sinn2ω1t,相当于移动荷载与简支梁的第n阶振型产生了共振,在此称速度VR=2kf1L为共振速度,对于k=1的情况,位移的共振放大系数最大,这种共振速度在文献[1,6,7]中也有介绍。
2.1.2 低阻尼情况(β≪1)
a)α≠k,β≪1
当梁体的阻尼很小时,可以忽略式(7)中包含β及β2的项,这时式(13)可以化为下面的形式,其与式(9)是极其类似的
(14)
虽然当α→k时,式(14)计算误差较大不再适用,但由于列车的实际行驶速度很难达到α=k的情况(即V=kVcr),同时实际桥梁结构的阻尼一般很小,因此,式(14)在工程实际中具有很高的实用性。
当荷载移动速度较低时(α≪1 ),且仅取桥梁的一阶振型来简化求解车辆在桥梁上行走时桥梁的位移响应,此时式(14)可简化为如下形式
(15)
b)α=k,β≪1
此种情况的推导与α=k,β=0的情况是类似的,下面直接给出梁体位移表达式
(16)
低阻尼情况和无阻尼情况具有很多类似的性质,比如无阻尼情况下得到的消振速度VD和共振速度VR在低阻尼情况下同样适用。
2.1.3 临界阻尼情况(β=βcr=k2)
当阻尼比ξk= 1时,说明此时桥梁的阻尼对于第k阶振型为临界阻尼,此时有
(17)
当n=k时,振型广义坐标qn(t)的积分变换形式可进行简化,此时简支梁第k阶振型对位移的贡献为
{(k2-α2) sinkωt-2kαcoskωt+
(18)
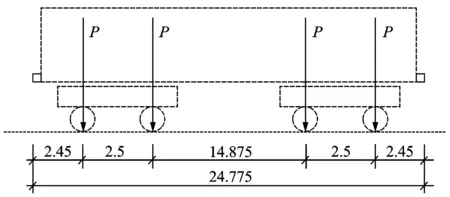
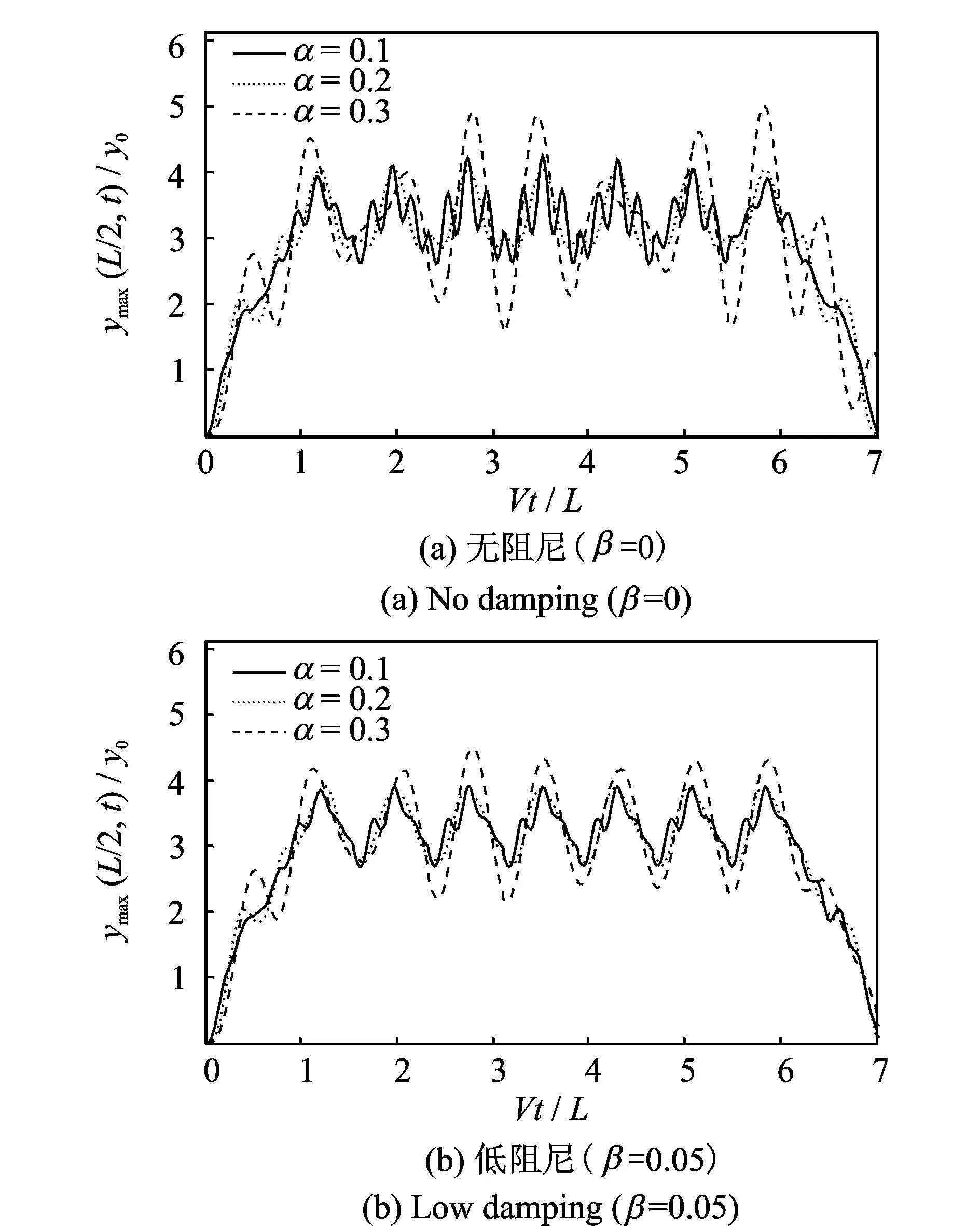
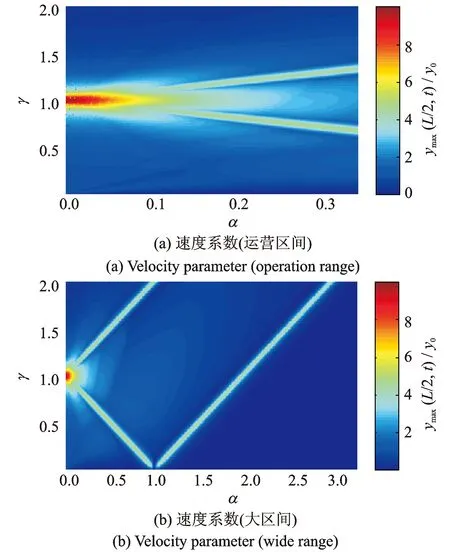
当β=βcr=k2时,并非对桥梁所有振型都是临界阻尼。对于桥梁的第n阶振型,如果n>k,此时桥梁的阻尼为低阻尼情况,可以按照式(7)求解第n阶振型的广义坐标qn(t);如果n 2.1.4 超阻尼情况(β>βcr=k2) (19) 同理,可得简支梁第n阶振型对位移的贡献为 (20) (21) (22) (23) βsinωt] (24) 根据上面的理论,编制计算程序,研究移动荷载通过简支梁时桥梁位移响应的振动特性。 列车荷载列参数:列车荷载列按照(3动+1拖)×2编组的德国ICE3高速列车的轮对位置布置,即选取荷载个数N=4×8=32;德国ICE3高速列车的动车和拖车轴距相同,具体如图3所示。 图3 德国ICE3列车的轴距 (单位:m) 对于简支梁跨中位移而言,梁第二阶振型的贡献量为零,因此以梁体1/4跨处的位移为例,研究荷载以不同速度过桥时简支梁各阶振型对梁体位移的贡献量。图4是利用不同桥梁振型阶数计算得到的梁体位移响应(相对值,以下同),图中实线及点线分别表示仅取简支梁的第一阶振型及前两阶振型计算得到的梁体位移。这里也计算了利用桥梁前3阶及3阶以上振型得到的梁体位移,它们与仅取前2阶振型得到结果几乎完全一致,说明其贡献很小,为简化分析,在此不再给出相应曲线。 图4 跨中位移与振型阶数关系图(β=0) 从图4中可以看出,当荷载移动速度较低时,梁体位移主要由桥梁的第一阶振型贡献,随着移动速度的提高,桥梁第二阶振型的位移贡献量逐渐增大,如当α=2时,点线最大位移响应仅为实线最大位移响应的一半。由于简支梁的第二阶振型对跨中位移的贡献量为零,在速度系数α=0~2的情况下,仅选取简支梁的第一阶振型计算梁体的跨中位移即可达到非常高的求解精度。 图5是无阻尼情况下,单个荷载以不同的速度过桥时梁体的位移响应。可以看出:在低速情况下,梁体跨中最大位移出现在荷载移动到跨中附近时,与文献[9]通过计算簧上质量过桥给出的结论一致;随着移动速度的增大,跨中最大位移出现时,荷载在桥上的位置逐渐向出桥方向移动;达到一定速度以后,跨中位移在荷载出桥时刻达到最大。 图5 跨中位移与时间及荷载速度关系图(β=0) 图6是无阻尼情况下,等间距移动荷载列以不同的荷载间距及速度过桥时梁跨中的最大位移响应,其中荷载间距lv= 0.1L~1.5L。 图6 跨中位移与荷载间距及荷载速度关系图(β=0) 从图6(a)中可以看出,当荷载列以某些特定速度过桥时,简支梁会出现共振响应。其中,共振速度与荷载间距lv的关系如下式所示 (25) 当i=1时,桥梁的位移响应最大。 从图6(b)中可以看出,沿式(25)所示的关系曲线,随着荷载移动速度的增大,梁体跨中的最大位移响应并非呈现单调增大趋势,而是在某些速度点处(即α=1/k,k为奇数)出现极小值,该速度即为本文定义的全消振速度。当荷载列以式(25)所示的速度通过简支梁时,两个相邻荷载的上桥时间间隔为iT1(T1为简支梁第一阶自振周期),说明移动荷载列引起的桥梁共振实质上是荷载列中单个荷载引起的桥梁余振响应的最大叠加。由于荷载以全消振速度通过简支梁时,桥梁的动力响应会在荷载出桥时刻趋近于零,因此,当由式(25)计算得到的共振速度同时为桥梁的全消振速度时,桥梁的共振响应将会被抑制。 图7是不同的桥梁阻尼情况下,荷载以不同速度通过简支梁时,梁体跨中的最大位移响应。可以看出:单个移动荷载通过桥梁时,桥梁最大位移响应并非随着速度的增大而单调增大,而是表现出一种类似正弦但波幅逐渐增大的形式,此趋势与文献[6,9,10]中通过计算簧上质量过桥得到的规律相同;列车荷载列过桥时,梁体的动力响应可视为由4个等间距移动荷载列引起动力响应的叠加,此时在某些速度点处桥梁出现共振[1],表现出一种完全不同的响应规律;阻尼的存在会减小梁体的最大位移响应,其对共振时桥梁的动力响应抑制更为明显。 图7 最大跨中位移与荷载速度及阻尼关系图 图8是在荷载出桥时刻(t=L/V),不同速度系数α所对应的梁体跨中位移。正如前面的讨论,单个移动荷载过桥时,在某些特殊速度下,梁体位移在荷载出桥时刻归零,低阻尼情况和无阻尼情况有着相同的变化规律。列车荷载列过桥时,在共振速度点处,桥梁位移响应出现峰值,表现出一种完全不同的响应规律。 图8 荷载出桥时跨中位移与荷载速度关系图 图9是不同的桥梁阻尼情况下,列车荷载列以不同速度过桥时,梁体跨中的位移时程。 图9 跨中位移时程曲线 从图9可以看出,低阻尼情况和无阻尼情况比较类似;随着速度的提高,跨中振动幅值增大;无阻尼情况下,当列车速度系数α=0.1,0.2时,梁体跨中位移在荷载列出桥时刻归零。 图10 动力放大系数与荷载频率及速度关系图(β=0.05) 可以看出,当速度系数很低时,有荷载移动产生的加载频率ω对桥梁位移的响应影响很小,位移响应表现出类似静力作用下的响应,即在速度系数α相同的条件下,当γ=1时桥梁位移响应最大;随着速度系数α的增大,由荷载移动产生的加载频率ω对梁体位移响应的影响逐渐加大,梁体在γ=1时的最大位移呈现逐渐减小趋势,而且在速度系数α相同的条件下,桥梁位移响应达到最大时,γ不再等于1。 1) 荷载移动速度较低时,简支梁的跨中位移主要由其第一阶振型贡献,随着移动速度的提高,高阶振型的位移贡献量逐渐增大。但在工程计算中,仅选取简支梁的第一阶振型计算梁体跨中位移即可达到非常高的求解精度; 2) 无阻尼情况下,桥梁跨中出现最大位移响应时的荷载位置随着速度的增大逐渐由跨中向出桥方向移动;桥梁最大位移响应随速度的增大呈现出一个类正弦波的形式。 3) 移动恒定荷载通过简支梁上时,在一定速度下会引起共振或消振现象。共振速度与移动荷载列的间距有直接关系,共振时桥梁的动力响应被放大;消振速度下,所引起的桥梁余振会在荷载出桥的时刻趋近于零。当共振速度同时又是消振速度时,共振现象会被抑制。 4) 移动简谐荷载作用下桥梁的位移响应同时受到加载频率及荷载速度的影响:当速度系数很低时,梁体位移在γ=1时达到最大响应;随着速度系数的增大,梁体在γ=1时的最大位移呈现降低趋势,且梁体位移响应达到最大时,γ不再等于1。 参考文献: [1] Xia H, Roeck G Re, J M Goicolea. Bridge Vibration and Controls [M], New York: Nova Science Publishers. 2011. [2] 高传伟, 唐雅茹, 余华. 基于移动荷载过桥的轨道交通桥梁振动研究[J]. 中国铁道科学, 2005,26(2): 73—76.Gao C W, Tang Y R, Yu H. Study on the vibration of rail transit bridge based on moving load passing bridge [J]. China Railway Science, 2005,26(2): 73—76. [3] 曹雪芹, 刘必胜. 桥梁结构动力分析[M]. 北京: 中国铁道出版社, 1987.Cao X Q, Liu B S. Dynamic Analysis of Bridge Structure [M]. Beijing: China Railway Publishing House, 1987. [4] Clough R, Penzien J. Dynamics of Structures [M]. Berkeley: Computers & Structures, Inc., 2003. [5] Yang Y B, Yau J D, Wu Y S. Vehicle-bridge Interaction Dynamics [M]. World Scientific Publisher, 2004. [6] 王少钦, 夏禾, 郭薇薇,等. 变速移动荷载作用下简支梁桥的动力响应及共振分析[J]. 振动与冲击, 2010,(2): 26—30.Wang S Q, Xia H, Guo W W,et al. Dynamic response and resonance analysis of simple bridge under speed-varying loads[J]. Journal of Vibration and Shock, 2010,(2): 26—30. [7] Xia H, Zhang N, Guo W W. Analysis of resonance mechanism and conditions of train-bridge system [J]. Journal of Sound and Vibration, 2006, 297: 810—822. [8] Fryba L. Vibration of Solids and Structures under Moving Loads [M]. London. Thomas Telford, 1999. [9] 肖新标, 沈火明. 移动荷载速度对简支梁动态响应的影响[J]. 西南交通大学学报, 2002,37(B11): 35—38.Xiao Xinbiao, Shen Huoming. Dynamic response of bridge under moving load [J]. Journal of Southwest Jiaotong University, 2002, 37(B11): 35—38. [10] Garinei A, Risitano G. Vibrations of railway bridges for high-speed trains under moving loads varying in time [J]. Engineering Structures, 2008, 30(3): 724—732.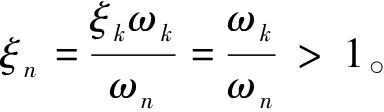
2.2 P(t)为简谐荷载
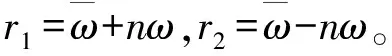
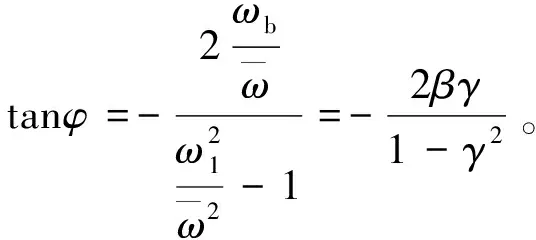
3 数值计算分析
3.1 模型参数
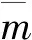
3.2 移动恒定荷载作用下桥梁的位移响应

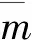
3.3 移动简谐荷载作用下桥梁的位移响应
4 结 论

