周向导波在不同连续性条件多层圆筒中的传播

张慧玲， 何 斌， 宋林辉， 尹晓春

(1.南京工业大学力学部，江苏 南京 211816；2.南京理工大学理学院，江苏 南京 210094)

引 言

多层厚壁圆筒结构，可以根据使用环境和使用功能的要求，对各层材料和结构进行设计，满足耐压、耐磨、耐高温、耐腐蚀等高性能要求，同时又可以节省高品质材料和制造费用。因此，多层圆筒是常用的一类工程结构件，在核反应堆结构、混凝土结构中的腐蚀监测、水下设备，智能结构，薄涂层结构和生物结构模拟等领域都有广泛的应用[1～6]。多层圆筒的疲劳裂纹往往萌生于层间界面。由于它具有曲面边界形式，波的反射特性复杂，导致“超声-回响”等传统的裂纹和缺陷的超声检测方法不能有效地进行检测。因此，需要提出新的有效的无损检测手段，避免裂纹扩展造成严重的后果。

超声导波是一种替代方法，它可以沿着层的方向传播，并在层厚方向形成驻波，具有较远距离、实时检测、充分利用结构几何特性的优势。目前梁、板等结构中导向波的传播已经得到广泛研究[7]，单层圆筒类结构中轴向导波的传播也已被研究[8]。Qu等也研究了圆环、轴筒结构等简单筒体类结构中周向导波的传播[9,10]。考虑到层间界面缺陷，本人已经研究了双层碳纳米管和双层圆筒等双层圆筒结构中的周向导波传播[11,12]。然而，多层圆筒结构的使用工况，更容易造成层间界面处萌生径向裂纹。从外层表面激发的的非轴对称型的周向导波，可以在某些激励频率下，使若干特定的波模态，在层间界面附近集中能量，从而能够检测出清晰的波群信号(反映波的能量传播特征)。因此，有必要仔细研究多层厚壁圆筒的周向导波波场的物理特性。本文研究了不同连续性条件的多层厚壁圆筒结构中周向导波的传播特性，考察了不同连续性条件对频散曲线和位移曲线的影响，为多层圆筒结构中，采用周向导波的无损检测方法来检测界面特性，提供理论依据。

1 周向导波问题的理论推导

不考虑体力时，第i层筒的位移运动方程为[13]

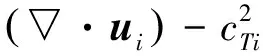
(1)

式中ui为第i层筒的位移矢量，Vi表示该层筒结构占有的空间区域，cLi和cTi分别是第i层筒的纵波波速和剪切波波速, 两波速依赖于第i层筒的材料质量密度ρi、Lamé常数λi和μi。第i层筒的边界条件为

=Fi在Si上

(2)

式中Si表示Vi的边界，n为边界上的外法线单位应力，▽ui表示位移梯度，T表示转置。

图1 多层圆筒结构横截面示意图

由矢量的Helmholtz分解，第i层筒的位移矢量场ui可分解为包含集散波标量势φi和等容波矢量势ψi的表达式

ui=▽φi+▽×ψi

(3)

式中 势函数φi和ψi满足如下波动方程

(4a)

(4b)

在平面运动中，矢量势ψi的只有z方向的分量，即

(4c)

采用分离变量法，可得

φi=fi(r)exp(inθ)exp(-iωt)

(5a)

ψZi=gi(r)exp(inθ)exp(-iωt)

(5b)

式中

(6a)

(6b)

式中Jn(x)和Yn(x)分别为n阶第1类和第2类Bessel函数。

采用极坐标系，第i层筒的位移分量为

(7a)

(7b)

由线弹性材料的Hooke定律，第i层筒的应力分量为

(8a)

(8b)

给定多层圆筒结构的内外表面都为自由表面，则边界条件为

(9)

在多层圆筒这一部分中，变量中的上标1表示内层圆筒， 上标i表示第i层圆筒，上标N表示外层圆筒。

对于光滑连接的多层筒，在接触面上，法向应力和法向位移都连续，切向应力为零，所以连续性条件表述为

(10a)

(10b)

(10c)

(10d)

对于固结连接的多层筒，在接触面上，应力和位移都连续，所以连续性条件表述为

(11a)

(11b)

(11c)

(11d)

将方程(6)代入方程(5)，然后代入方程(7)～(9)和(10)，或和(11)，得到一个含有4N个未知常量A=[A1,B1,C1,D1,…,Ai,Bi,Ci,Di,…,AN,BN,DN，CN]T的4N阶齐次方程组。为了分析问题方便，对变量采取无量纲化处理，令

最后得到表达式

[dmn]A=0

(12)

(13)

这就是多层圆筒中周向导波的频率方程。

频率方程(13)求解之后，代入方程(12)，就可以求出非零特征矢量A=[A1,B1,C1,D1,…,Ai,Bi,Ci,Di,…,AN,BN,CN,DN]T。然后把特征矢量A代入方程(6)，再代入方程(5)和(3)，得到周向导波的位移波型分量

ur(r,θ,t)=Ur(r)exp(inθ)exp(-iωt)

(14a)

uθ(r,θ,t)=Uθ(r)exp(inθ)exp(-iωt)

(14b)

其中

(15)

式中W(r)为一个2×4N阶矩阵。

2 数值计算及讨论

考虑到计算量太大，以表1和2中的参数为数值算例，研究周向导波在不同类型多层厚壁圆筒中的传播特性。

表1 材料参数

表2 几何参数

2.1 频散曲线的基本特征

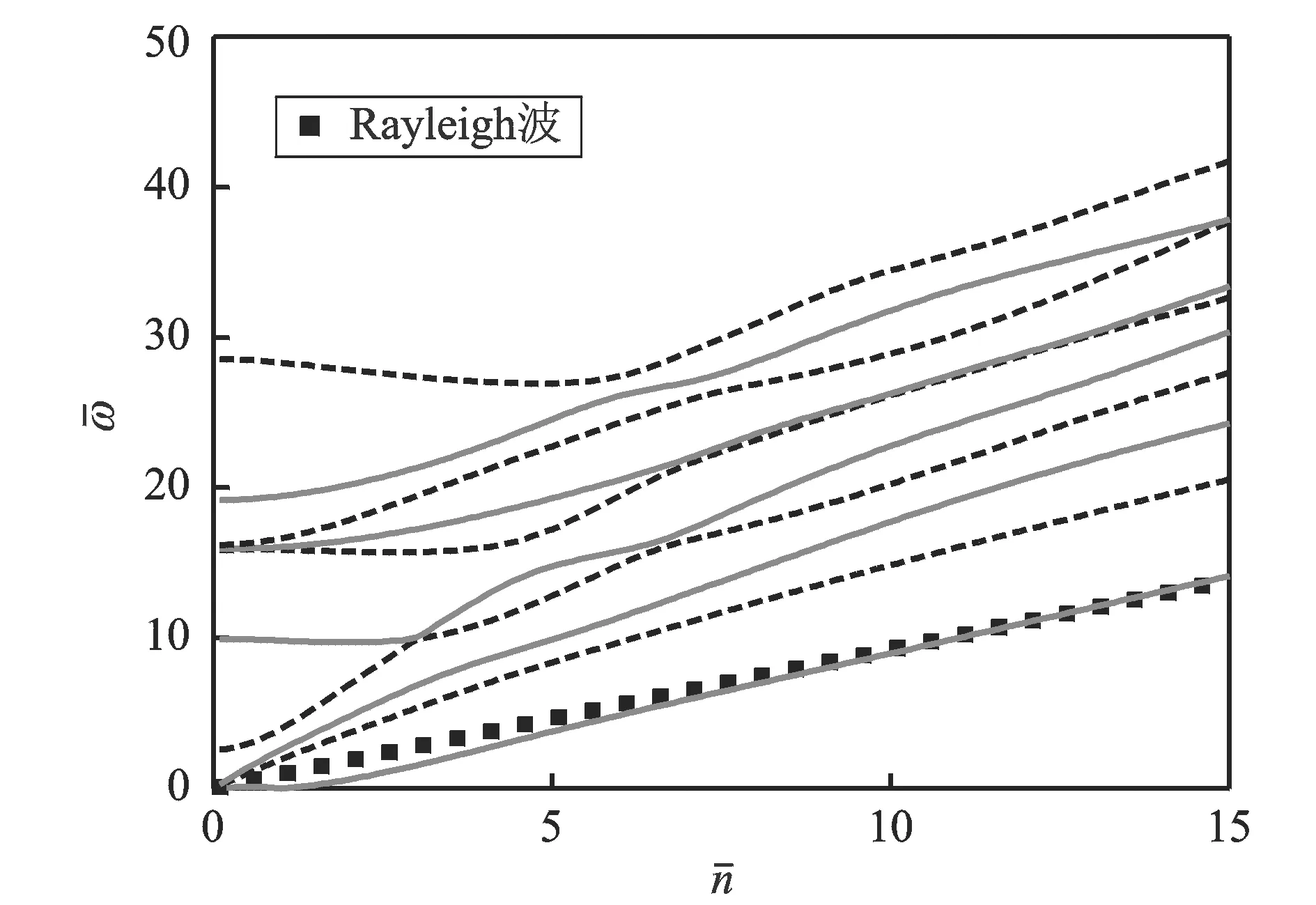
图2 三层光滑连接钢筒中周向导波频散曲线的最初10阶模态和Rayleigh波

2.2 连续性条件对频散曲线的影响

以表2中的光滑连接和固结连接两种连续性条件的三层钢筒TSST和TWST为例，并将它们和三组单层钢筒STST，SIST和SOST的频散曲线一起比较，研究连续性条件对频散曲线的影响。

图3(a)，(b)，(c)，(d)分别为三层圆筒与单层圆筒的频散曲线第1～4阶模态比较，从图3(a)～(d)可以看到，固结三层圆筒TWST的频率始终高于光滑连接三层圆筒TSST，可见光滑连接方式降低了多层圆筒的频率。而对于固结多层圆筒，由其连续性条件特点可知，它在层间界面上的位移与应力均应保持连续一致。也就是说，固结的多层筒实际上就应该和一个同材料、同尺寸的单层圆筒性质完全一致，而图3中的曲线完全印证了这一点，即所有模态中固结三层钢筒TWST与同尺寸同材料的单层钢筒STST的频散曲线完全一致。

从图3(a)～(b)中可以看出，在低阶模态时，三层钢筒TSST和TWST，都比较接近于内层钢筒SIST的频散曲线，特别是光滑连接三层钢筒TSST，在第1阶模态时，频散曲线非常接近于内层钢筒SIST。说明此时内层筒对多层筒的低阶模态频散曲线起主导作用，特别对于光滑连接的多层圆筒来说，用具有第1阶模态的外激励周向导波检测内层筒的裂纹和缺陷更加有效。图3(c)和(d)还显示，对于第3阶和第4阶模态，三层钢筒TSST和TWST的频率始终低于单层内筒和外筒的频率。特别是在比较高的频率时，三层钢筒TSST和TWST都与具有相同内外径的单层筒STST频率非常接近，说明层间界面效应开始弱化，对于同一高阶模态，与双层筒相比[12]，多层筒和同厚度的单层筒曲线要在较高波数时才会出现重合，因此多层筒比双层筒的层间弱化要慢。但是同样像双层筒一样[12]，对于三层筒及至多层筒，也可以得出一个重要结论，检测层间界面裂纹的周向导波的选择范围，应该集中于低阶模态上。

图3 三层圆筒与单层圆筒的频散曲线第1～4阶模态比较

2.3 壁厚对频散曲线的影响

以表3中的变壁厚的三层钢筒为例，每层钢筒(表1中材料参数)取相同的厚度，层间光滑接触，研究壁厚对多层圆筒频散曲线的影响。

表3 几何参数

图4(a)～(f)分别为不同壁厚三层圆筒的频散曲线第1～6阶模态比较，从图4中可以看出，在1阶模态时，壁越厚频率越大，而且差别很大。对于2至4阶模态，频散曲线比较接近，壁厚对频散曲线影响很小；而对于5阶以上模态，随着筒壁越来越薄，频率越来越高。因此，对于周向导波的无损检测方法，选用受壁厚影响较小的2至4阶模态的周向导波，来检测多层筒界面的裂纹和缺陷更加有效。

2.4 连续性条件对位移曲线的影响

(16)

并作正规化处理，即除以各自的最大位移值得

(17)

图4 不同壁厚三层圆筒的频散曲线第1～6阶模态比较

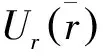
图5 光滑连接位移波型图

图6 固结连接位移波型图

由前面的工作知，检测多层圆筒层间界面裂纹的周向导波选择范围，可能应该集中于低阶模态上。再由图5(b)和图6(b)合成位移分布，无论是光滑连接还是固结连续性条件，多层筒第2阶模态能量同样也集中在界面附近，进一步证实了第2阶模态最具有检测界面裂纹的应用价值。因此，像双层筒一样[12]，应该将变频器设置成优先激发具有第2阶模态频率的周向导波，以实现对界面裂纹的无损检测目的。

3 结 论

(1)周向导波在多层厚壁圆筒中传播时，虽然理论公式和双层筒不一样，但是进行数值分析时发现了许多相同和不同的地方。多层筒同样也会发生明显的频散现象和模态干涉现象，但是多层筒的模态干涉现象更为频繁。

(2)通过和同厚度的单层筒频散曲线比较，发现高阶模态时两者都出现层间界面弱化现象，但是对于同一高阶模态，多层筒和同厚度的单层筒曲线要在较高波数时才出现重合，因此多层筒比双层筒的层间弱化要慢。

(3)从合成位移曲线来看，多层筒进一步说明了第二阶模态具有检测界面裂纹的重要价值，因为它在多层筒的所有界面处都具有集中能量的特点。

参考文献：

[1] Martin D G. Considerations pertaining to the achievement of high burn-ups in HTR fuel[J]. Nuclear Engineering and Design，2002, 213: 241—258.

[2] 李学金，林文山，范平，等. 钢筋腐蚀光纤传感器的研究[J]. 测控技术， 2001，20(8): 10—13.

[3] Ratcliffe C P, Ratcliffe C P, Crane R M. Santiago A L. Experimental modal analysis comparison of the vibration damping properties of composite cylinders measured in-air and underwater[J]. The Journal of the Acoustical Society of America， 1996, 100(4): 2585.

[4] Wu C P, Syu Y S, Lo J Y. Three-dimensional solutions of multilayered piezoelectric hollow cylinders by an asymptotic approach[J]. International Journal of Mechanical Sciences， 2007, 49: 669—689.

[5] Terrón J M, Sánchez-Lavega A, Salazar A. Multiple scattering of thermal waves by a coated subsurface cy-lindrical inclusion[J]. Journal of Applied Physics. 2001, 89(10): 5 696—5 702.

[6] Yang W, Fung T C, Chian K S, et al. Instability of the two-layered thick-walled esophageal model under the external pressure and circular outer boundary condition[J]. Journal of Biomechanics. 2007, 40: 481—490.

[7] Ryden N, Lowe M J S. Guided wave propagation in three-layer pavement structures[J]. The Journal of the Acoustical Society of America, 2004, 116(5): 2 902—2 913.

[8] Gazis D C. Exact analysis of the plane-strain vibrations of thick-walled hollow cylinders[J]. The Journal of the Acoustical Society of America, 1958, 30(8): 786—794.

[9] Liu G, Qu J. Guided circumferential waves in a circular annulus[J]. ASME Journal of Applied Mechanics, 1998, 65: 424—430.

[10] Valle C, Qu J, Jacobs L J. Guided circumferential waves in layered cylinders[J]. International Journal of Engineering Science, 1999, 37: 1 369—1 387.

[11] Zhang H L, Yin X C. Guided circumferential waves in double-walled carbon nanotubes[J]. Acta Mechanica Solida Sinina, 2007, 20(2): 110—116.

[12] 张慧玲，尹晓春. 层间光滑接触的双层厚壁圆筒周向振动导波[J]. 振动工程学报，2008，21(5): 471—475.Zhang H L, Yin X C. Guided circumferential waves in a double-layered thick-walled hollow cylinder with a free-sliding interface[J].Journal of Vibration Engineering, 2008，21(5): 471—475.

[13] Achenbach J D. Wave Propagation in Elastic Solids[M]. Amsterdam：North-Holland, 1984.