车辆传动系统线性弯扭耦合振动响应灵敏度研究

黄 毅， 刘 辉,2， 陈胤奇， 项昌乐,2

(1.北京理工大学机械与车辆学院， 北京 100081；2.北京理工大学车辆传动重点实验室, 北京 100081)

引 言

灵敏度分析的概念起源于电路设计，为达到整体性能最佳，需找出对整体性能影响最大的那些原件。这就是电路设计中灵敏度分析的概念。齿轮传动系统振动特性直接影响机械系统和机械装备的性能和工作可靠性[1]，因此，研究齿轮传动系统动态特性以及灵敏度分析具有重要意义。

机械结构灵敏度分析的目的是对结构进行动态优化，主要包括固有频率问题、振型问题和动力响应振幅问题。其中固有频率问题和振型问题的灵敏度分析统称固有特性灵敏度分析。早期文献在研究系统动态特性时以研究固有特性为主，希望通过修改和优化参数避免机械结构共振的发生或减小发生共振时的振型，以此为目的进行固有特性灵敏度分析能使参数修改和优化更具目的性。R G Parker等以复合行星排为对象[2,3]，分别研究了调谐和失谐系统中固有特性对设计参数的灵敏度，并将其简化成与应变能/动能成比例的表达式，仅获得模态应变能/动能的情况下就能在定性和定量上获得对某阶模态影响最大的参数。文献[4,5]建立集中质量模型，应用系统矩阵法推导了定轴齿轮系统纯扭转振动固有特性对实际系统模型参数的灵敏度公式。文献[6]利用实模态理论计算分析了系统各阶固有频率对转动惯量和刚度的灵敏度，得到了系统的固有频率分布规律和物理参数对固有频率的影响。

在车辆传动系统中，由于发动机的工作转速在一个相对较宽的范围之内，有时不管如何对设计参数进行修改都不能将所有共振频率移出到工作转速之外；或者在某转速下虽然发生了共振现象但共振幅值很小，此时不足以对车辆传动系统造成破坏影响；更进一步的情况是对传动系统振动特性的分析从线性领域扩展到非线性领域以后传统的线性固有特性的概念不再存在。所有这些都要求对车辆系统动态特性的分析从固有特性的分析转向关于动态响应的分析。目前对系统振动响应灵敏度的研究还基本停留在理论研究的阶段，张义民等针对直接法和摄动法进行灵敏度分析时会产生长期项的问题[7]，在对灵敏度方程解耦的基础上，结合傅里叶级数有效消除了长期项并给出了消除长期项判断法则。林家浩等对简单线性系统采用简谐激励和脉冲激励分析了动态响应对设计参数的灵敏度[8]，但其方法仍是基于模态灵敏度的基础上演化而来。在车辆传动领域，刘辉等建立线性纯扭转集中质量模型[9]，并采用直接求导法推导了扭振角位移和轴段附加扭振应力对轴系刚度的灵敏度计算公式。但并未考虑弯曲方向对扭转自由度的影响和耦合作用。在很多情况下，振动能量是在弯曲方向上通过轴承传到箱体引起振动和噪声。本文在纯扭转模型的基础上考虑了轴和齿轮在弯曲方向上的弹性以及轴承的弹性作用，以线性弯扭耦合模型为基础，进行附加扭转力矩和轴承支反力对设计参数灵敏度研究，以获得更为精确的计算结果，并对实际问题中基于响应灵敏度进行参数优化和动力学修改等应用提供理论依据。

1 动力学方程组的建立

车辆传动系统包括齿轮、轴承和离合器等部件，此处将不同部件用统一表达式进行表述。齿轮啮合部分采用平均啮合刚度，忽略综合传动误差等参数激励以及齿侧间隙和偏心等非线性因素。采用拉格朗日法建立齿轮系统动力学方程组，每个质量点在3个自由度方向表达式如下式所示

(1)

式中x，y为平动位移；θ为扭转位移；mj和Jj为质量点j质量和转动惯量；Fb表示弯曲方向上同一根轴上各质量点间相互作用力，Tt表示两质量点间扭转力矩，Fn表示质量点所承受的横向作用力，如果质量点j为轴承，Fn表示轴承支反力；如果质量点j为齿轮，Fn表示齿轮啮合力；如果质量点j为离合器，Fn为零；Tn表示齿轮副啮合力矩，当质量点j为轴承和离合器时，Tn为零，各量表达式如下：

如果质量点j为轴承，有

(6)

如果质量点j为齿轮，有

(7)

式中Rj为所在齿轮基圆半径；Kij为第i根轴上第j个质量点的轴段弯曲刚度，Cij为相应轴段的弯曲阻尼；ktj-1j和ktjj+1为质量点j-1与j，j与j+1间轴段的扭转刚度，ctj-1j和ctjj+1为相应扭转阻尼；kxj和kyj为轴承支承刚度，cxj和cyj为相应支承阻尼；kmk和cmk为第k对齿轮副啮合刚度和阻尼，以上刚度和阻尼均为不随时间变化的定值；αk为第k对齿轮副主被动轮之间位置角，βk为其压力角；Δk为第k对齿轮副啮合线变化量，其表达式为

(8)

2 响应灵敏度方程组的建立

直接法求灵敏度物理概念明确，数学推导简单，数值计算方便，又可进行从一阶到高阶的灵敏度分析，故采用直接求导法建立灵敏度方程组。将通用化动力学方程组对参数a进行求导，a为扭转刚度、转动惯量和轴承支承刚度等参数。对动力学方程组用直接求导法建立的灵敏度方程组(1)如下式

(9)

其中，各量表达式为

式(12)中当a=ktj-1j，有

当a≠ktj-1j有

如果质量点j为轴承，由式(6)可推得灵敏度方程

(13)

如果质量点j为齿轮，由式(7)可推得灵敏度方程

其中

(15)

3 算例分析

3.1 系统力学模型

利用集中参数法对某车辆传动系统样机进行建模。该样机能实现8个前进挡位和4个倒挡，CH，BL，BR，C1，C2，C3，C4为换挡离合器，本文将以4挡为例进行灵敏度的分析，4挡为离合器BL和C4结合，其他离合器分离。另外系统还包括1个输入惯量盘、2个输出惯量盘、11个轴承、7个离合器、4对定轴齿轮副和2个简单行星排共计42个质量点，每个质量点包括x，y和θ三个方向自由度共计126自由度，其动力学模型如图1所示。

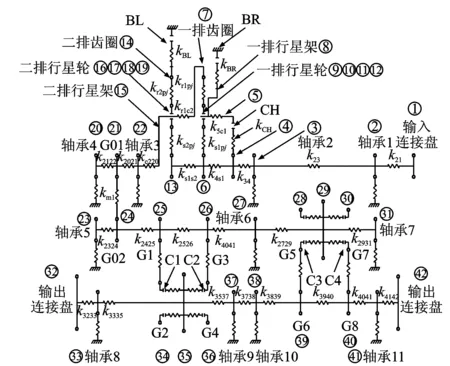
图1 某样机弯扭耦合振动模型

对如图1所示传动系统采用发动机输入，发动机在全油门额定转速，输入转速4 200 r/min，其输入转矩如图2所示。对质量点32和42施加大小相等的负载。计算工况取4挡进行计算。根据式(4)可将响应的一次物理量θ转化为各质量点间轴段的附加扭转力矩。在系统输入转速为4 200 r/min时，各轴段附加扭转力矩最大值的计算结果如图3所示。可以看出附加扭转力矩较大的轴段为20-21,24-25,25-26,26-27,27-29等5段轴。

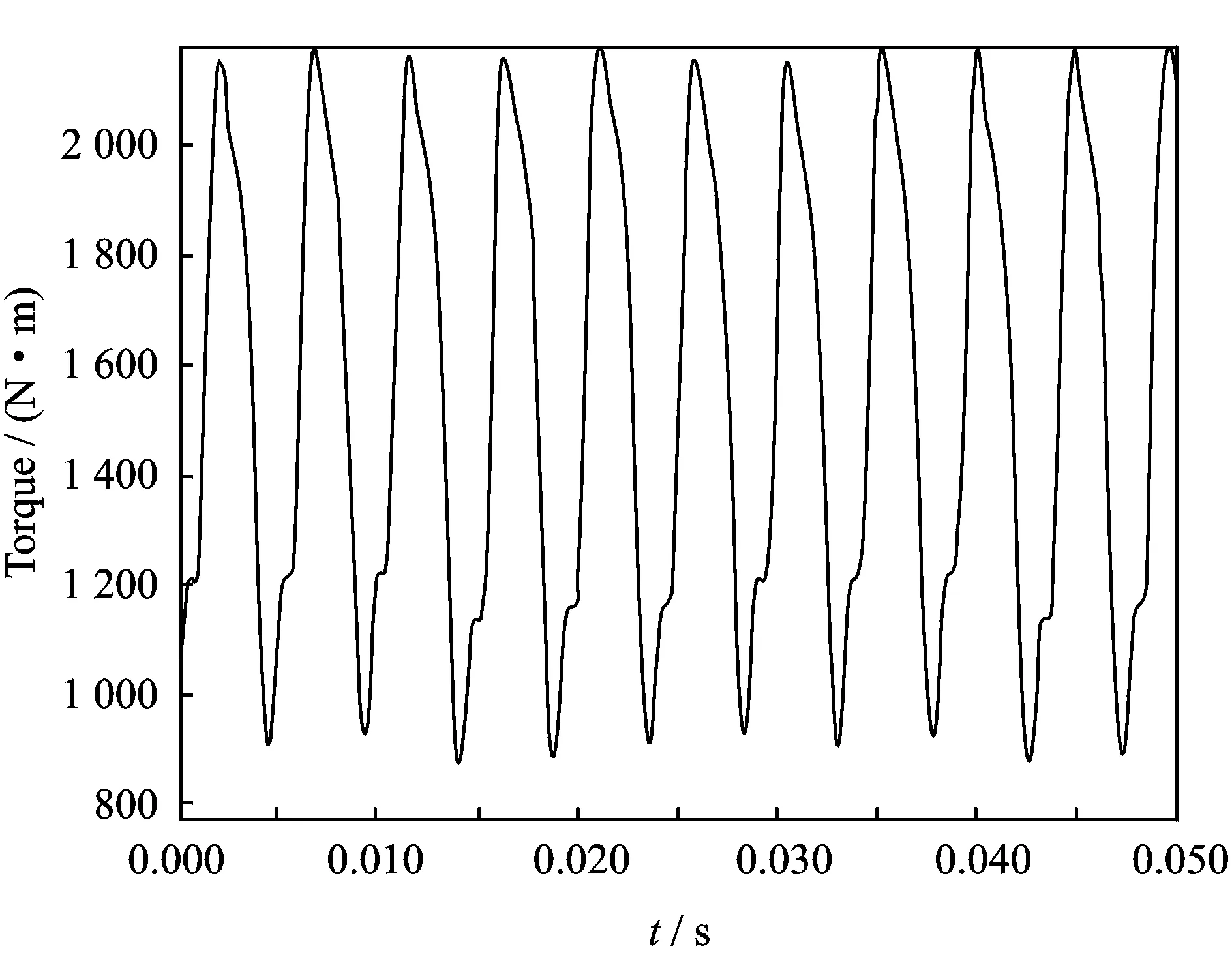
图2 发动机输入转矩

图3 系统各轴段附加扭转力矩波动幅值

3.2 轴段附加扭转力矩对轴段扭转刚度灵敏度

在工程实际中，通常采用调整轴段扭转刚度的方法进行动力学修改。在进行轴段的选取时，首先选取前面5段附加扭转力矩较大的轴段，一轴上选取1-2，s1-s2，21-22以及三轴上选取32-33，33-35，37-38，40-41，41-42共计13个轴段为对象研究其对各轴段扭转刚度的灵敏度，设计参数选取了22段轴扭转刚度。计算通过Matlab编程进行，每个灵敏度程序运行时间约7 min，总时间共计154 min。

根据式(12)定义的灵敏度，此时取a=kti进行轴段附加扭转力矩对各轴段扭转刚度灵敏度计算，其结果如图4所示。

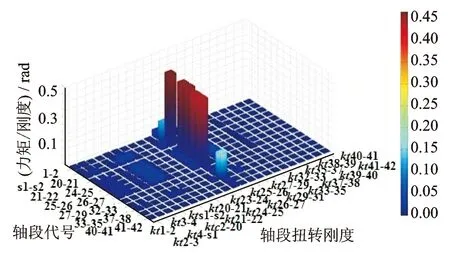
图4 各质量点间轴段附加扭转力矩对各扭转刚度灵敏度

图4所得结果是系统输入端转速为4 200 r/min，输入转矩为如图2所示波形的情况下所得。其中x坐标为各轴段的扭转刚度，y坐标为参与灵敏度比较的13段轴段代号。从左往右剖开来单独看每一轴段对扭转刚度的灵敏度，可以发现各轴段间灵敏度在趋势上趋于一致，各轴段附加扭转力矩对kt25-26的灵敏度高于对其他扭转刚度的灵敏度。接下来对附加扭转力矩影响较大的扭转刚度有：kt 1-2，kt 2-3，kt s1-s2，kt c2-20，kt 24-25，kt 27-29，对这6个量的灵敏度基本处于同一数量级。从表1和图1中可以看出同处在二轴的扭转刚度kt 25-26和kt 29-31的大小明显小于该轴上其他扭转刚度的数值大小，但各轴段附加扭转力矩仅对kt 25-26灵敏度高，而对kt 29-31灵敏度较低，通过观察力矩的传递可以发现kt 25-26在传递路线上，kt 29-31不在传递路线上，结合同样不在传递路线上的扭转刚度kt 21-22，附加扭转力矩对其灵敏度也较低，但kt 21-22本身数值并不明显小于该轴上其他扭转刚度，因此可以认为附加扭转力矩对不在传递路线上的扭转刚度灵敏度低。在一轴上扭转刚度普遍较小， 从图4上可以看出各轴段附加扭转力矩对一轴上各扭转刚度的灵敏度并没有明显高出其他灵敏度的情况出现。因此可以认为出现灵敏度数值较高的情况是由扭转刚度较大的轴段中夹杂一个较小扭转刚度的轴段引起的。

表1 轴段扭转刚度列表

在比较不同轴段对同一扭转刚度灵敏度时发现，不管选哪一扭转刚度为对象，灵敏度高的情况始终出现在轴段20-21，24-25，25-26，26-27，27-29和37-38这6段轴上。从图3可以看出，这6段轴的附加扭转力矩较其他轴段的附加扭转力矩高。

结合上面的分析，可以看出影响附加扭转力矩对扭转刚度灵敏度主要因素有两点：其一是某一轴上是否存在扭转刚度明显小的轴段；其二，该轴段是否具有较大附加扭转力矩。

3.3 轴段附加扭转力矩对质量点惯量灵敏度

在设计阶段，由于可以选择系统中各部件的尺寸等参数来获得对各质量点质量/惯量属性的选取。因此往往将惯量作为可研究的宏观参数进行灵敏度分析。在参数选取时，选取各轴承、齿轮的转动惯量并将轴的惯量等效到各质量点上。对于行星传动部分，选取了太阳轮、齿圈和行星架的质量进行灵敏度分析。设计参数选取了30个质量点转动惯量，每个灵敏度程序运行时间约6 min,总时间共计180 min。其输入条件如前所述，不同轴段附加扭转力矩对各质量点惯量灵敏度如图5所示。

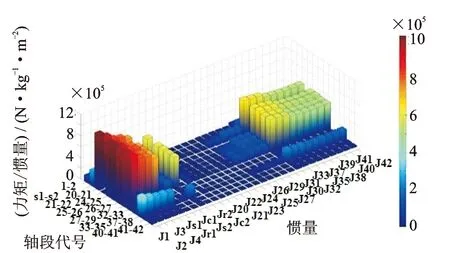
图5 各质量点间轴段附加扭转力矩对各质量点转动惯量灵敏度

在图5中从左往右剖开来看每一轴段对各点惯量的灵敏度，可以发现各轴段间灵敏度在趋势上趋于一致，只不过存在数值上的差异。在趋势上各轴段对各质量点惯量的灵敏度数值较大的情况出现在J1,J2,J3,J4,Js1,Js2以及三轴上各质量点的惯量上。通过表2可以看出，以上惯量大小各异，并没有同时大或者同时小的情况出现。因此，可以认为其灵敏度大小同轴系结构相关，与本身惯量的大小并无太大联系，对附加扭转力矩的影响较大的惯量出现在一个系统的输入和输出端。

表2 质量点惯量列表

而研究同一惯量对不同轴段的影响时，从图中可以看出不管选哪一质量点惯量为对象，灵敏度高的情况始终出现在轴段20-21,24-25,25-26,26-27,27-29和37-38这6段轴上。而从图3可以看出，这6段轴的附加扭转力矩较其他轴段的附加扭转力矩高。因此，可以认为不同轴段对同一惯量灵敏度与该轴段本身的附加扭转力矩的大小相关，当该轴承受较大附加扭转力矩时，其对惯量的灵敏度也较高。

3.4 纯扭和弯扭模型下轴段附加扭转力矩对设计参数灵敏度比较

为了解在弯扭模型下灵敏度规律同纯扭模型的区别，采用文献[9]中的方法对本文研究对象建立了纯扭模型。纯扭模型下，系统动力学方程(1)变成为下式

(16)

其中，Tt定义同式(4)和(5)。如果质量点j为轴承，有

Tnj=0

如果质量点j为齿轮，有

此时有

Δk=R2k-1θ2k-1+R2kθ2k

相应的，灵敏度方程(9)变成

(17)

其中，∂Tt/∂a定义同式(12)。如果质量点j为轴承，有

如果质量点j为齿轮，有

此时有

以质量点20和21间轴段附加力矩为例，在纯扭转模型和弯扭耦合模型下对各轴段扭转刚度和质量点惯量灵敏度如图6(a)和图6(b)所示。

图6 纯扭和弯扭模型下灵敏度比较

从图6(a)可以看出，在趋势上，质量点20和21间轴段附加扭转力矩对各扭转刚度的灵敏度在纯扭模型和弯扭下规律和趋势一致，其附加扭转力矩对各质量点惯量灵敏度如图6(b)所示，也能得出相同结论；但是具体到数值大小，弯扭模型下由于考虑了轴、轴承以及齿轮的弯曲变形，其灵敏度值小于将以上因素考虑为刚体的纯扭模型。表3中给出了质量点20-21间的轴段附加扭转力矩对各扭转刚度的灵敏度在纯扭和弯扭模型的情况下动态灵敏度的各自幅值以及它们的对比信息，可以看出对于大部分灵敏度在弯扭模型下的计算结果比在纯扭模型下的计算结果小10%～20%。其他轴段的情况也类似，在此不在赘述。

表3 不同模型中轴段20-21间附加扭转力矩对扭转刚度灵敏度幅值比较

因此可以认为将弯曲方向上考虑为弹性体时的弯扭耦合模型计算出来的灵敏度是小于将弯曲方向上考虑为刚体时的纯扭转模型计算出来的灵敏度，加上弯曲方向的弹性后一部分能量会转移到弯曲方向上，因此减小了扭转方向上设计参数对附加扭转力矩的影响。

3.5 轴承支反力对轴承支承刚度灵敏度分析

车辆传动系统在工作过程中振动和噪声不仅在扭转方向上存在，在横向上同样存在。横向上的力是造成箱体变形的主要因素，其对齿轮传动系统的稳定性和安全性造成一定程度的影响。

公式(6)对轴承支承刚度ki求偏导可获得支反力对轴承支承刚度灵敏度。当i≠j时，表达式即为公式(13)所示；当i=j时有

(18)

根据式(13)和(18)计算样机中11处轴承所受支反力对支承刚度的灵敏度，计算结果如图7所示。

图7 各轴承支反力对支承刚度灵敏度

根据图7以某一轴承支反力对支承刚度的灵敏度为例发现，轴承支反力首先是对轴承本身的支承刚度灵敏度高，除此之外就整个系统而言各支反力对轴承3、轴承5、轴承6、轴承7、轴承9、轴承10支承刚度灵敏度较高。对于轴承1和轴承2而言，它们的支反力对另外9个轴承的支承刚度灵敏度都较低；对轴承1支反力影响较大的支承刚度是轴承1本身和轴承2的支承刚度，对轴承2支反力影响较大的支承刚度是轴承2本身；对于一轴左侧的两轴承，轴承3支承刚度对各支反力的影响明显大于轴承4；对于二轴上三轴承而言，它们对各支反力影响都较大，其中轴承6支承刚度对二轴上其他两轴承以及三轴上部分轴承的支反力都有较大影响；对于三轴上四轴承的支承刚度而言，中间两轴承即轴承9和轴承10对三轴上各支反力都有较大影响。

因此，调整某轴承支反力首先是考虑到该轴承本身的支承刚度，除此之外对整个系统而言影响较大的支承刚度有轴承3、轴承6、轴承9、轴承10；对于轴承1和轴承2的支反力而言，它们对另外9个轴承的支承刚度都不敏感，其中轴承2的支承刚度对两者影响大于轴承1。

结合各轴承支反力的大小发现，本身支反力大的轴承对各支承刚度的灵敏度也相对较大。从能量的角度出发来看，在某些设计参数变化之后能量大的轴承能量变化率也较大，这同之前扭转方向上灵敏度结论相同。不同之处在于弯曲方向上，各轴承支反力还和同一轴上各质点之间力的相互制约相关，这种情况下除了本身支承刚度对自身支反力影响较大还需要找出系统中对其他轴承支反力影响较大的轴承支承刚度。

3.6 轴承支反力对各点质量灵敏度

除了上述因素，也对各点质量对轴承支反力的影响进行了分析，其结果如图8所示。

图8 各轴承支反力对各点质量灵敏度

根据图8以某一轴承支反力对各点质量的灵敏度为例发现，对各支反力影响较大的质量点包括m1，m2，m3，m4，ms1，ms2以及三轴上从m32到m42的各点质量。这同各质量点惯量对扭转力矩的影响规律类似。以某一质量为例研究对各支反力的影响发现，影响最大的支反力有轴承3、轴承4、轴承5、轴承6、轴承7、轴承10、轴承11，且各质量的规律类似。

因此，为改变各轴承支反力调整各点质量的规律和扭转方向的规律类似。改变质量/惯量参数同时对扭转方向的力矩和弯曲方向的力都能起到较大作用。

4 结 论

本文以某样机系统为研究对象，建立了包含弯曲和扭转方向自由度的动力学模型，并考虑两个方向的耦合作用。通过拉格朗日法建立多自由度动力学方程组，并采用直接求导法获得灵敏度方程组，分别从横向和纵向分析轴段附加扭转力矩和轴承支反力对刚度和质量/惯量的灵敏度，结论如下：

1)考虑了轴、轴承和齿轮弯曲变形的弯扭耦合系统计算出来的附加扭转力矩对设计参数灵敏度与纯扭模型大小排序规律类似，但是由于弯曲方向上考虑为弹性以后的耦合作用，一部分能量分配到弯曲方向上造成弯扭耦合模型的灵敏度数值略小于相对应纯扭模型的数值。

2)影响附加扭转力矩对扭转刚度灵敏度主要因素有两点：其一是某一轴上是否存在扭转刚度明显小的轴段；其二，该轴段是否具有较大附加扭转力矩。

3)附加扭转力矩对各质量点惯量的灵敏度和轴承支反力对各点质量的灵敏度规律类似，本身的力/力矩大，其对同一质量/惯量参数灵敏度较大；从本文来看,对某一轴段附加扭转力矩/轴承支反力影响大的质量点位于输入和输出附近的各质量点。

4)从各轴承支反力对各轴承支承刚度的灵敏度来看，影响最大的首先是各轴承本身的支承刚度；其次由于同一轴上各点在弯曲方向上的力互相作用，因此需要找出对整个系统各轴承支反力影响最大的那几个轴承支承刚度，如本文系统中的轴承3、轴承6、轴承9、轴承10的支承刚度。

5)从能量的角度来看，能量大的各轴段(扭转方向附加扭转力矩)或轴承(弯曲方向支反力)对某一设计参数的灵敏度也越大。

参考文献：

[1] 王建军，李润芳，李其汉.齿轮系统非线性振动研究进展[J].力学进展,2005,35(1):37—51.Wang J J, Li R F, Li Q H. Research advances for nonlinear vibration of gear transmission systems[J]. Advances in Mechanics, 2005,35(1):37—51.

[2] Guo Yichao, Robert G Parker. Sensitivity of general compound planetary gear natural frequencies and vibration modes to model parameters[J]. Journal of Vibration and Acoustics, 2010,132(011006):1—13.

[3] Lin J, Parker R G. Sensitivity of planetary gear natural frequencies and vibration modes to model parameters[J]. Journal of Sound and Vibration, 1999,228(1):109—128.

[4] 项昌乐,廉晓辉,周连景.针对实际传动系统的灵敏度分析与动力学修改[J].中国机械工程,2006,17(3):325—328.Xiang C L, Lian X H, Zhou L J. Sensitivity analysis and dynamic modification based on the physics model of vehicular powertrain[J]. China Mechanical Engineering, 2006,17(3):325—328.

[5] 邵毅敏,张奎,李小侠.基于灵敏度分析的车辆传动系统扭振分析及仿真[J].长沙理工大学学报,2009,6(3):1—5.Shao Y M, Zhang K, Li X X. Torsional vibration analysis and simulation of the vehicle driveline based on sensitivity[J]. Journal of Changsha University of Science and Technology, 2009,6(3):1—5.

[6] 蔡仲昌,刘辉,项昌乐,等.车辆行星传动系统扭转振动固有特性及灵敏度分析[J].中国机械工程,2011,22(1):96—101.Cai Z C, Liu H, Xiang C L, et al. Research on natural characteristics and sensitivity for torsional vibration of a vehicle multistage planetary gears[J]. China Mechanical Engineering, 2011,22(1):96—101.

[7] 张义民,闻邦椿,刘巧伶.动力响应灵敏度分析中的长期项消除[J].振动工程学报,1998,11(4):462—466.Zhang Y M, Wen B C, Liu Q L. Elimination of secular terms from sensitivity analysis of Dynamic responses[J]. Journal of Vibration Engineering, 1998,11(4):462—466.

[8] 林家浩.结构动力优化中的灵敏度分析[J].振动与冲击,1985,(1):1—6.Lin J H. Sensitivity analysis in structural dynamic optimization[J]. Journal of Vibration and Shock, 1985,(1):1—6.

[9] 刘辉,蔡仲昌,曹华夏.车辆动力传动系统扭转强迫振动响应灵敏度研究[J].兵工学报,2011,32(8):939—944.Liu H, Cai Z C, Cao H X. Sensitivity analysis of forced torsional vibration on vehicle powertrain[J]. Acta Armamentarii, 2011,32(8):939—944.