基于ANSYS/LS-DYNA 的弹带挤进过程仿真
马帅,张相炎,游修东,2
(1.南京理工大学,江苏 南京 210094;2.中国人民解放军91388 部队,广东 湛江 524022)
0 引言
弹带挤进是一个瞬态过程,持续时间短,弹丸运动行程也不大,但其对内弹道的影响却很大。传统的实验方法,只能通过分析挤进结束后的弹带或者通过其他间接物理量来推测挤进过程的一些参数,这要求实验者有丰富的经验。随着计算机技术的发展,现在的有限元仿真已经能够模拟微秒甚至更短时间内的动力学过程,利用有限元软件,可以获得挤进过程的完整的动力学响应。
1 计算模型
1.1 有限元模型[1]
现代的火炮膛线为了减小磨损和挤进的冲击,一般采用渐速膛线,而本文研究的是弹带的挤进过程,该过程弹丸行程不大,因此忽略膛线缠角的变化,取膛线的缠角为固定值。因该过程只涉及到身管很有限的一部分,为了节省计算量,只对身管的一部分进行建模,挤进的有限元模型见图1。
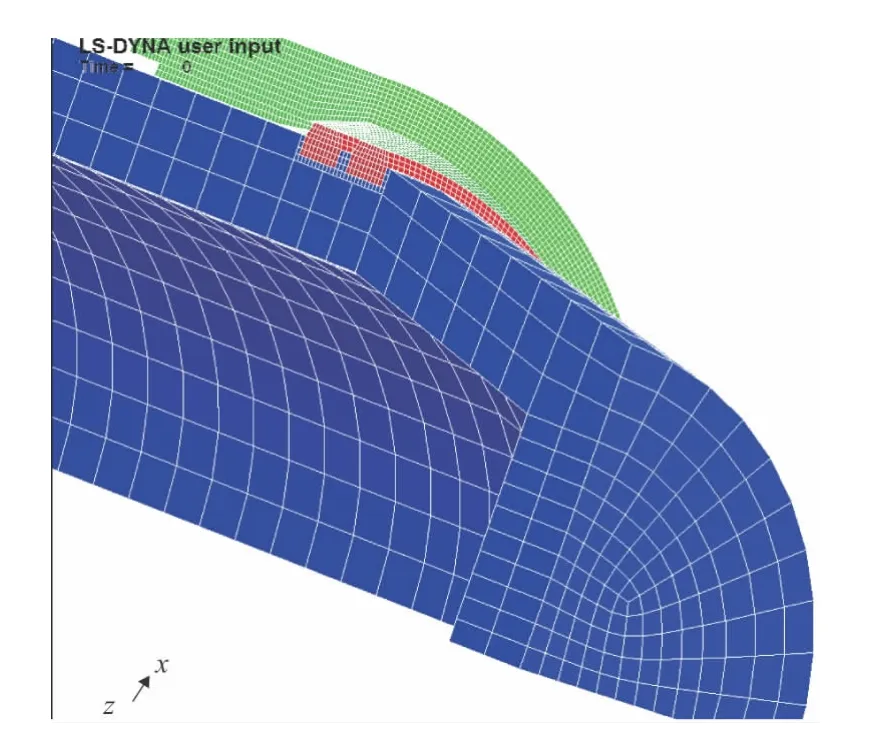
图1 挤进过程的有限元模型
整个模型分为弹丸、弹带和身管三个部件,这三部分都是采用八结点的六面体单元SOLID164 来划分的。这种单元生成刚度矩阵时采用的是单点积分,采用单点积分可能会发生沙漏模式,为了防止沙漏模式,需要打开沙漏控制。实践已经证明,单点积分在显示动力学分析中有很好的精度,同时大大减少了计算量。
在身管的后端面加固定约束,这与实际发射过程相符,弹丸和弹带通过共结点的方式连接在一起,这种连接方式是对实际的一种很好的近似,而且可以大大减少计算量。为了简化处理,只在弹底加压力,由于弹丸挤进过程中摆动很小,这也是对实际的一种很好的近似。由于要模拟弹丸的旋转,载荷曲线跟实际越相近越好,本文用线性增加的压力来近似。
由于弹丸的摆动,挤进过程中会发生弹丸和身管的接触以及弹带和身管的接触,定义弹丸和身管的接触为自动接触,定义弹带和身管的接触为侵蚀接触,这种接触曾普遍用于弹丸的侵彻等。弹丸从0 开始加速,且速度变化范围较大,在挤进结束时可达100 m/s 以上,因此不能将摩擦系数定义为常数,LS-DYNA 采用的是指数衰减的摩擦定律,见式(1):
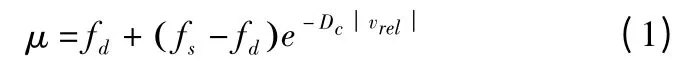
其中:fd为动摩擦系数,fs为静摩擦系数,Dc为衰减系数,vrel为相对滑动速度。
1.2 材料模型
弹丸采用LS-DYNA 中的刚体材料模型,刚体材料模型需给定密度,弹性模量和泊松比,这是为了计算弹丸的惯性并准确地计算接触。弹带材料选择的是紫铜,采用的是Johson-Cook 材料模型,该材料模型综合考虑了应变、应变率和绝热温升对应力的影响,非常适合模拟瞬态的动力学过程。身管材料选某炮钢,采用等向强化的弹塑性材料模型。Johson-Cook 材料模型见式2:

其中:A,B,C,n,m 均为材料常数,εp为有效塑性应变,ε*为相对应变,T=(T- Troom)/(Tmelt- Troom)为相对温度变化。
对于材料的失效,LS-DYNA 采用累积损伤模型,累积损伤模型定义一个损伤变量D,初始时D=0,当D=1时材料失效,单元被删除,D 的定义见式(3):

其中:Δεp为塑性应变增量,εf为材料发生失效时的应变,见式(4):
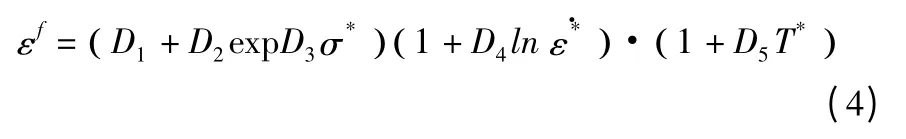
其中:D1~D5皆为材料常数,一般通过实验测定,σ*=p/σeff为应力三轴度,p 为由状态方程求得的压力,σeff为Von mises 有效应力。
2 挤进过程仿真结果及分析
2.1 挤进过程结果
图2-图7 显示了挤进过程中弹带的应力云图。

图2 挤进前:σeff/105 MPa

图3 坡膛挤压第一条弹带,未刻槽:σeff/105 MPa
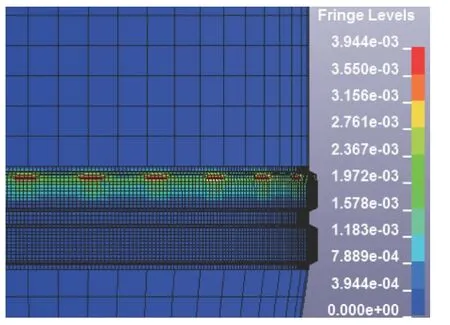
图4 第一条弹带开始刻槽:σeff/105 MPa
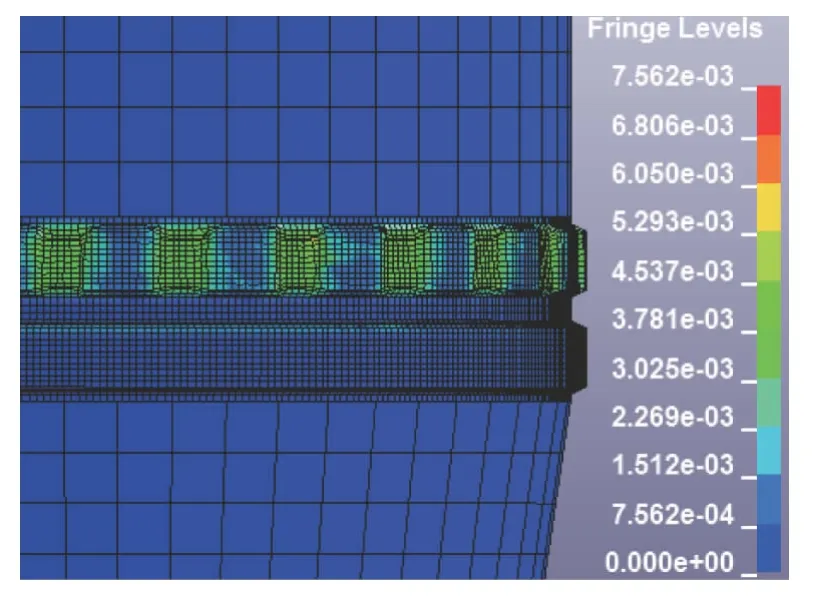
图5 坡膛挤压第二条弹带:σeff/105 MPa
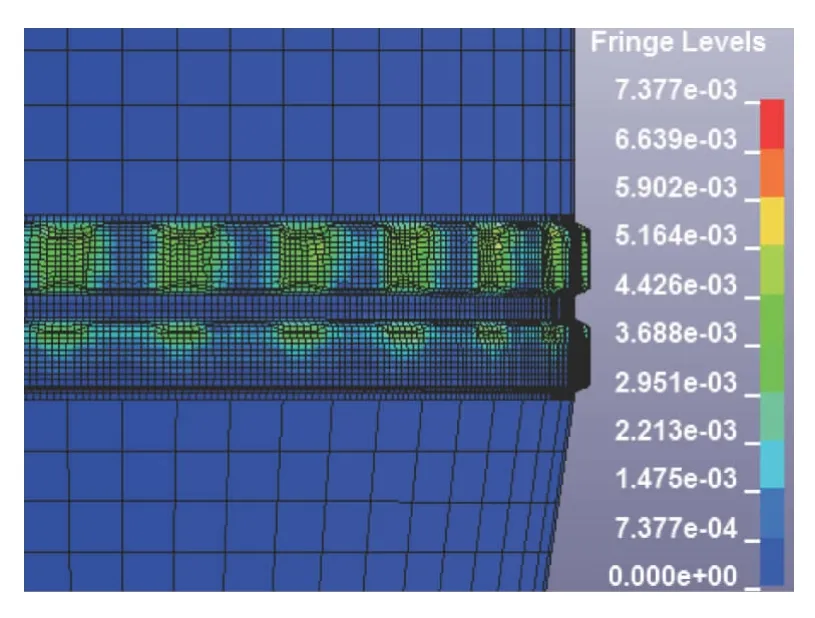
图6 第二条弹带开始刻槽:σeff/105 MPa
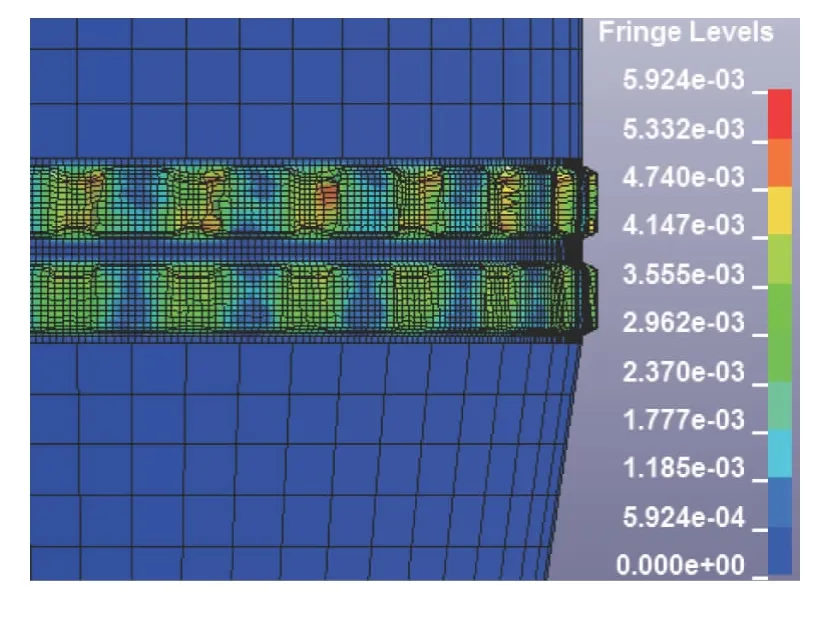
图7 挤进完成:σeff/105 MPa
图2-图7 展示了弹带挤进的详细过程,但所刻槽的倾角不太明显,这是由于弹丸的惯性比较大,其转动有一个滞后效应。由图4 与图6 可以看出,弹带的最大应力位于挤进所刻槽的前部,这表明膛线和弹带刚发生接触即处于较高的应力状态,这种应力冲击可能是膛线磨损的一个原因。因为材料制造过程中不可避免的会有一些缺陷,如微裂纹、微孔洞等,在强的剪切应力下或受到应力冲击,极易导致裂纹扩展,使材料发生破坏或磨损[2]。
2.2 单元应力结果
图8 为某些单元的应力曲线。由于采用的是单点积分单元,该种单元为常应力单元,因此用LS-DYNA 只能得到单元应力结果,而非结点应力。曲线A 和曲线B 可以看出两条弹带对单元应力的影响,曲线都有两个明显的峰,由于挤进速度随时间在增加,第一个峰在时间上宽一些。曲线A 和曲线B 所代表的两个单元材料相同,但A单元的应力却比B 单元大很多。通常认为,应力大的地方磨损也较快,A 单元位于膛线起始部,这可以解释为什么膛线起始部磨损较快[3]。曲线C 为弹带上的单元,该单元在挤进开始后应力几乎不变,表明该处的材料处于塑性流动状态,符合对铜这种材料的认知。以上分析表明,本文的应力计算结果符合实际,可以为实验研究提供理论依据。
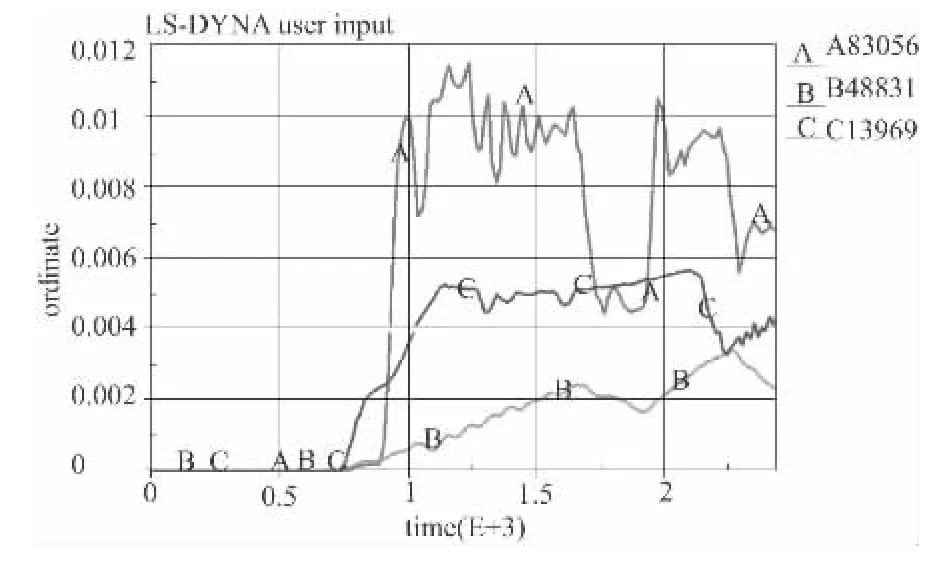
图8 单元的von mises 应力-时间曲线:σeff/105Mpa
3 挤进阻力的计算及分析
图9 和图10 分别为弹丸加速度和位移曲线。由达朗贝尔原理可知,物体所受的力和它的惯性力是平衡力系。对弹丸做轴线方向的受力分析,弹丸受到弹底压力,挤进阻力和惯性力,利用matlab 对数据进行处理,便可求出挤进阻力随时间的变化,再结合图10 位移随时间的变化曲线,即可得挤进阻力随挤进行程的曲线,见图11。

图9 弹丸加速度曲线
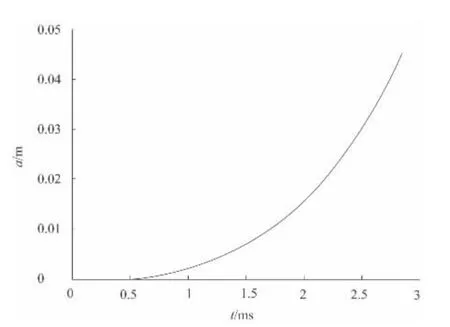
图10 弹丸位移曲线
图12 为文献[4]求得的挤进阻力曲线,张浩等通过对实际物理过程所做的一系列假设,对挤进过程进行了理论分析,分阶段得出了挤进阻力的公式。
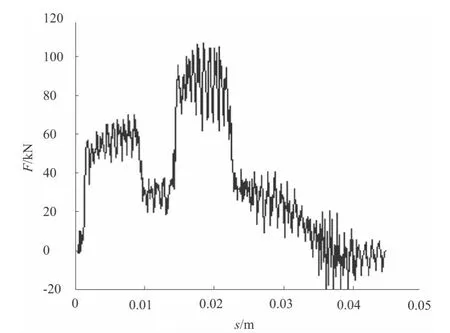
图11 挤进阻力随挤进行程的曲线
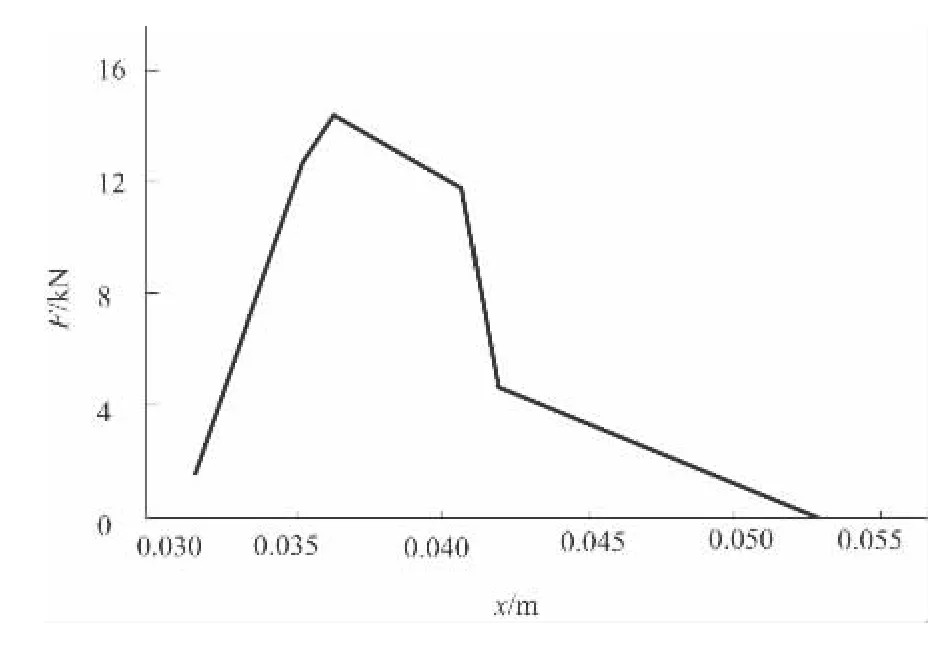
图12 文献[4]得到的理论解
将图11 中第一条弹带的挤进阻力曲线(挤进行程在0.014 m 以前的部分)与图12 进行对比,可以发现两者的变化趋势基本相同,两者都是在弹带与坡膛发生接触到开始刻槽前的这一段位移中阻力急剧上升,在外侧刻槽完毕后阻力开始急剧下降,两者之间是一个阻力缓慢变化区间。但文献[4]是一小口径火炮的结果,而本文是对某一大口径火炮求得结果,两者数值显然不同。通过两条曲线的对比,表明本文的曲线可以体现挤进过程中挤进阻力的变化规律,而且有限元分析可以得到双弹带对挤进阻力的影响。
4 结语
基于ANSYS/LS- DYNA 对弹带挤进过程进行了仿真,通过输出关键时刻的图形,展示了整个挤进过程中弹带的变形规律,然后通过分析模型中某些单元的应力曲线,对膛线起始部的磨损提出了看法。通过仿真获得的加速度曲线和速度曲线,基于达朗贝尔原理,利用matlab 对数据进行处理,得到了挤进阻力曲线,通过与文献[4]阻力曲线的对比,验证了文中计算结果的正确性,表明ANSYS/LS-DYNA 是研究挤进过程的一个很好的工具。
[1]谈乐斌,张相炎,管红根,等.火炮概论[M].北京:北京理工大学出版社,2005:49-57.
[2]孙河洋,马吉胜,李伟,等.坡膛结构变化对弹带挤进过程影响的研究[J].振动与冲击,2011,30(3):30-33.
[3]米粮川,高树滋,赖长缨.内弹道弹带挤进过程仿真研究[J].弹箭与制导学报,2012(2),32(1):133-135.
[4]张浩,周彦煌.埋头弹火炮挤进过程研究[J].弹道学报,2006,18(1):76-79.

