某型火炮膛线优化研究

杜中华

（军械工程学院，石家庄 050003）

0 引言

膛线的出现是枪炮技术发展史上的一次重大革命。一方面，膛线和弹丸配合使得火药气体的密封性更好，枪炮射程更远；更重要的是，旋转的膛线使弹丸旋转起来，弹丸的飞行稳定性变好，枪炮射击精度大大提高。目前大部分枪炮都有膛线。

膛线在结构上是枪炮身管内表面制造出的与身管轴线具有一定倾斜角度的螺旋槽。膛线对炮膛轴线的倾斜角叫缠角，按照缠角从膛线起始部向炮口方向的变化规律，膛线通常分为三种类型：缠角不变的为等齐膛线；缠角逐渐增大的为渐速膛线；由膛线起始部的渐速段和炮口部的等齐段组成的膛线为混合膛线。目前大部分火炮尤其是定型较早的火炮都采用等齐膛线，其加工较为简单；一些炮口初速较小的榴弹炮则采用渐速膛线，其加工较为复杂；随着膛线加工水平的提高尤其是数控加工设备的采用，膛线加工在技术上的障碍已经很小，目前国内少数新型火炮已经开始采用混合膛线。

膛线的选取与膛线导转侧力有很大关系，膛线起始部导转侧力过大会加剧身管的磨损，炮口部导转侧力过大会影响射击精度。目前火炮膛线类型和膛线曲线参数主要依靠经验来进行选取，缺少行之有效地数学模型，很难实现优化。文中以某型线膛火炮身管为研究对象，尝试建立以膛线导转侧力为核心的数学模型，对膛线类型和膛线曲线进行优化。文中的研究方法可以为各种枪炮身管的膛线设计提供借鉴。

1 膛线导转侧力模型[1-4]及常见膛线曲线方程[1-3]

弹丸在膛内运动时，弹带与膛线导转侧间的相互作用力即导转侧力Fn。

对于渐速膛线，其表达式为

式中：n为膛线条数；ρ为弹丸惯性半径；r为弹丸半径；S为炮膛横断面积；pd为弹底压力；α为缠角；x为弹丸直线行程；m为弹丸质量；v为弹丸直线速度。

对于等齐膛线，由于缠角α为固定值，其导转侧力表达式可简化为

等齐膛线的膛线展开为一直线；渐速膛线的膛线展开则为一曲线，常见的曲线方程包括：

式中，a、b均为结构参数。

2 火炮膛线优化模型

2.1 假设

膛线缠角变化会影响弹丸前进的阻力，由于目前膛线缠角都比较小，通常不超过8°，其引起阻力的改变与作用在弹丸底部的火药气体推力相比可以忽略不计。故文中假设膛线的优化不会影响膛压和弹丸直线运动速度。

2.2 自变量的选取

由于身管膛线长度一定，且混合膛线中渐速段在膛线起始部，选取渐速段长度l1与身管膛线总长度l的比值γ作为第一个自变量。γ在0～1之间变化，当γ为0时，膛线类型为等齐膛线，当γ为1时，膛线类型为渐速膛线，当0<γ<1时，膛线类型为混合膛线。

要保证弹丸的飞行稳定性，弹丸出炮口时的旋转速度必须满足一定的要求，也就是炮口处缠角必须满足一定要求。优化膛线时将炮口处缠角α1（也是渐速段的末缠角）作为确定值考虑。膛线起始部初缠角α0可以发生变化，将其作为第二个自变量。α0在0和α1之间变化，当α0=α1时，膛线类型即等齐膛线。

以膛线起始部为原点建立直角坐标系，膛线展开曲线必然要经过原点，另外曲线各处的斜率与tanα是相等的，综合考虑式（3）和式（4），我们选取更为一般的曲线方程（6）作为渐速膛线曲线方程：

选定指数b作为第三个自变量，b≥1。

考虑三种膛线类型，从膛线起始部到炮口，膛线缠角要么逐渐增大，要么保持不变，是不可能减小的。也就是说，=tanα向炮口方向是不能减小的。考察正弦曲线式（5）的导数=abcosbx，由于a、b均大于0，随着x从0开始增大，导数却在减小。故膛线曲线不能采用正弦曲线形式。

最终选择渐速段比例γ、膛线初缠角α0、指数b作为膛线缠角优化模型的自变量，渐速段曲线方程如式（6）所示。

以某型线膛火炮身管为背景，上述3个自变量确定后，就可以用Matlab编制通用程序绘制膛线展开曲线并计算膛线各个截面上的导转侧力。

γ为0时得到等齐膛线展开曲线和导转侧力分别如图1和图2所示；γ为1时得到渐速膛线展开曲线和导转侧力分别如图3和图4所示；γ为0.6时得到混合膛线展开曲线和导转侧力分别如图5和图6所示，

2.3 目标函数

火炮沿身管长度方向上阳线磨损的一般规律如图7所示，膛线起始部磨损较大，炮口也有一个较大的磨损段[2]。膛线磨损影响火炮身管的使用寿命，炮口段磨损还影响射击精度，故这两部分的导转侧力要重点考虑。这里将膛线划分为3段：膛线起始段、中间段和炮口段。膛线起始段从0到lm+1.5d，炮口段从lg－2d到lg，两段中间为中间段，如图6所示。炮口起始段、中间段和炮口段的最大导转侧力依次为Fn1、Fn2、Fn3，取3段的权值分别为3、1和2（权值可以根据需要调整），最终目标函数为：F=3Fn1+Fn2+2Fn3。对膛线的优化归结为使目标函数F最小。

3 火炮膛线优化研究

3.1 自变量影响分析

图1 等齐膛线展开曲线

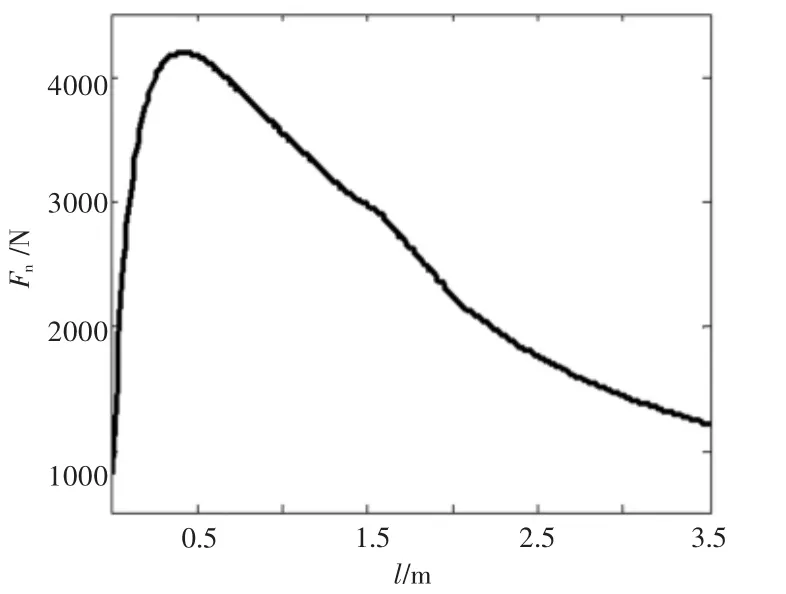
图2 等齐膛线导转侧力

图3 渐速膛线展开曲线

图4 渐速膛线导转侧力

图5 混合膛线展开曲线

图6 混合膛线导转侧力

以γ=0.9，α0=0o，b=2为标准条件，依次改变各自变量来观察目标函数F的变化。F随γ的变化如图8所示，γ取0.9左右，F有最小值，此时膛线为混合膛线，膛线大部分为渐速，只在炮口处有很小一段等齐。F随α0的变化如图9所示，α0取0左右，F有最小值，此时初缠角为0°，弹丸很容易切入膛线。F随b的变化如图10所示，b取2.3左右，F有最小值。取3个自变量正交变化观察目标函数如图11所示，发现当γ=0.9，α0=0o，b=2.3时，F有最小值14 842 N。

3.2 优化研究

图7 沿身管长度上阳线磨损的一般规律

上述自变量影响分析时，自变量均按照等差变化且这个等差值不可能无限小，所以上述分析只能是一种粗略分析。为实现膛线优化，还需要用到专门的优化算法。这里采用常规非线性优化算法、模拟退火算法和遗传算法分别对该问题进行优化[6-10]，分别对应Matlab中的fmincon、simulannealbnd和ga算法。fmincon和simulannealbnd算法需要给定优化初值，simulannealbnd和ga算法具有随机性，为研究算法的稳定程度，每种算法进行5次优化，使用Matlab中的默认算法参数和终止规则。三种算法的优化结果分别如表1、表2和表3所示。可以看出，对于该优化问题，fmincon和simulannealbnd算法对优化初值较为敏感，不同优化初值得到不同的优化结果，或者说这两种算法容易陷入局部极小值。ga算法则比较稳定，几乎每次都能寻到全局最优解。

图8 F随γ的变化曲线

图9 F随α0的变化曲线

图10 F随b的变化曲线

图11 F随3个自变量的变化曲线

表1 fmincon算法优化结果

表2 simulannealbnd算法优化结果

表3 ga算法优化结果

图12 优化后膛线展开曲线

图13 优化后膛线导转侧力

最终优化结果为：γ=0.9514，α0=0o，b=2.2506，目标函数为14351 N。优化后的膛线展开曲线和导转侧力曲线分别如图12和图13所示。膛线为混合膛线，其中渐速段比例为0.9514，渐速段膛线展开曲线为：y=2.1463×10－6x2.2506。从图12也可以看出，膛线起始段和炮口段导转侧力都十分小，达到了优化目的。

4 结论

目前线膛枪炮对于膛线类型和膛线曲线的选取主要依靠经验，还没有一套较为科学的方法。文中尝试建立某型火炮的膛线优化模型，为线膛枪炮设计提供依据。文中编制了涵盖三种膛线类型和常见膛线曲线的导转侧力计算通用程序，选定渐速段比例、膛线初缠角和方程指数为优化变量，以减小膛线起始段和炮口段导转侧力为准则确定目标函数，据此建立了某型火炮的膛线缠角优化模型。在影响因素分析基础上，尝试用非线性优化算法、模拟退火算法和遗传算法对该问题进行优化，得到了满意的优化结果。同时发现，遗传算法对于该问题具有很好的稳定性。研究也发现，目前文献中推荐的正弦曲线形式的渐速膛线对应膛线缠角是渐小的，在实际中是不适用的。

[1] 张相炎,郑建国,袁人枢.火炮设计理论[M].北京:北京理工大学出版社,2014.

[2] 潘玉田.炮身设计[M].北京:兵器工业出版社,2007.

[3] 易声耀,张竞.自动武器原理与构造学[M].北京:国防工业出版社,2009.

[4] 张小兵.枪炮内弹道学[M].北京:北京理工大学出版社,2014.

[5] 薛定宇,陈阳泉.基于Matlab/Simulink的系统仿真技术与应用[M].北京:清华大学出版社,2002.

[6] 云庆夏.进化算法[M].北京:冶金工业出版社,2000.

[7] 康立山,谢云,尤矢勇,等.非数值并行算法:第1册 模拟退火算法[M].北京:科学出版社,1994.

[8] 刘勇,康立山,陈毓屏.非数值并行算法:第2册 遗传算法[M].北京:科学出版社,1995.

[9] 刑文训,谢金星.现代优化计算方法[M].北京:清华大学出版社,1999.

[10] 王小平,曹立明.遗传算法—理论、应用与软件实现[M].西安:西安交通大学出版社,2002.