三角网格曲面上离散曲率改进算法

马献德，谢小峰

1.南京电子技术研究所一部，南京210039

2.南京禄口国际机场动力技术部，南京211113

1 引言

曲率是曲面上一点附近的重要局部几何性质，对于有精确解析形式的曲面模型，其上任一点处的曲率可以根据其坐标，由经典的微分几何方法的解析公式直接计算[1]。对于没有精确解析形式，而只有表面离散点坐标数据及离散点之间拓扑关系的曲面模型，则只能完全借助于待求曲率的点附近各点的分布以及相互之间的拓扑关系，采用数值方法求解。求解曲面上一点处的曲率是获取该曲面几何信息的重要步骤，在离散几何、计算几何、计算机图形学、虚拟现实技术等许多领域广泛应用。

由离散曲面上一点的邻近局部点计算离散曲率，一般先把离散点划分为网格曲面模型，根据待求点各邻近网格的几何信息计算待求点处的曲率。

Chen等[2]在1992年提出，将经典微分几何和曲面论中描述法曲率n、主曲率k1和k2与主方向e1和e2之间关系的Euler公式改写为参数形式，并以圆弧拟合法和最小二乘法求解法曲率参数，从而计算主曲率。此方法容易实现，但圆弧拟合对真实的离散曲面而言过于粗糙，精度不高。

Taubin等[3]在1995年根据曲面微分几何特性，以n、e1和e2积分构造一个矩阵B，并证明B的特征向量就是n、e1和e2，特征值中就包含了k1、k2。通过待求曲率的顶点的邻近三角面加权求和来估算矩阵B，进而计算主曲率。

M eyer等[4]在2003年采用离散化Laplace-Beltram i算子并积分来直接计算平均曲率kh，采用离散化Gauss-Bonnet定理直接计算Gauss曲率kg，并进而求解主曲率。

Dong等[5]在2005年提出基于弧长参数微分计算法曲率的方法，即点p1处的一个法曲率可由点p1及其附近一点p2的法向量及两点各自坐标估算。在此基础上借助上述Chen等提出的方法求解主曲率和主方向，克服了Chen法中圆弧拟合有时导致很大误差的问题。

此外，还有M oreton等[6]提出的拟合法，Chen等[7]提出的重心加权法，Page等[8]提出的法向量投票法，柯映林等[9]提出的通过Shepard曲面插值点线性组合法等。

其中，M eyer的方法具有简明的几何意义，简单易行，计算结果能达到一定的精度，且计算量较小。文献[10]对多种算法进行了对比分析，认为M eyer方法的计算效果最优。

经分析发现，此方法的主要计算步骤可以通过转换得以简化，在计算精度和效率上可得到改进。

2 M eyer方法概述

M eyer提出的计算平均曲率kh和高斯曲率kg的方法[4]为：

其中，N1(pi)是pi的所有直接邻近点（与pi共边的点）的集合，n为pi点处的曲面单位法向量。vij=pj-pi，其余依此类推。符号·表示向量内积运算。各参数的定义如图1所示。

图1 离散曲率计算参数示意图

AMixed称为混合面积，其定义如下：其中，AΔijk是Δpipjpk的面积，而AΔijk，V为Δpipjpk当Δpipjpk为锐角三角形时，图2中四边形ohkpihj的面积（点o为Δpipjpk的外心）。

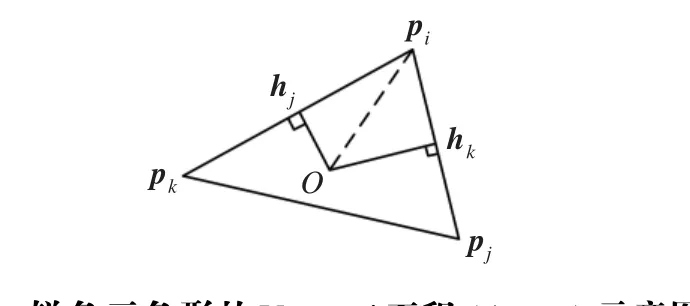
图2 锐角三角形的Voronoi面积(AΔijk，V)示意图

上述公式需要多次计算三角函数值、反三角函数值，由于涉及到三角形的边长、面积的计算，还需要多次开平方，计算中容易引入截断误差和舍入误差，且计算效率较低。以下试图精简计算步骤，提高计算精度和计算效率。

假设pi共有m个直接邻近点，从而有m个邻近三角面（即有一个顶点为pi的三角面），pi及其所有直接邻近点的直角坐标，pi处的曲面单位法向量n均已知。研究目标是根据这些已知条件，以最精简的计算步骤完成以M eyer方法计算pi的离散平均曲率和离散Gauss曲率的过程。设

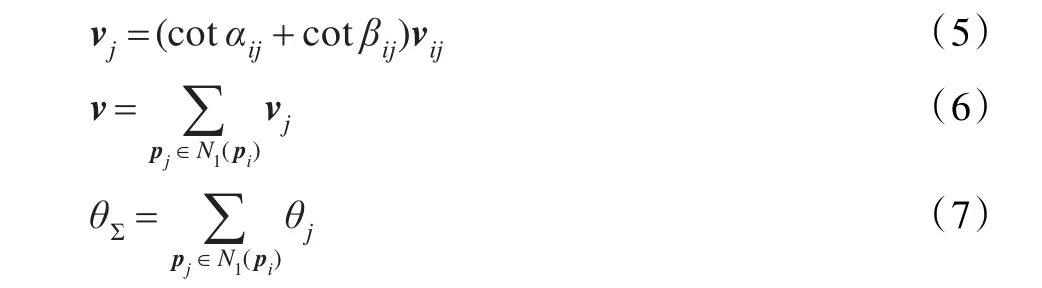
把v称为平均曲率构造向量，把θΣ称为Gauss曲率构造角。可见v、θΣ、AΔijk，V的计算是算法中的主要步骤，决定了整个计算过程的计算量。以下分别寻找这三个参数的改进算法。

3 对平均曲率构造向量的改进算法设计

3.1 平均曲率构造向量的普通算法简述

一般通过计算三角形三边长来计算公式（5）中的两个余切值，则计算vj的步骤如下：

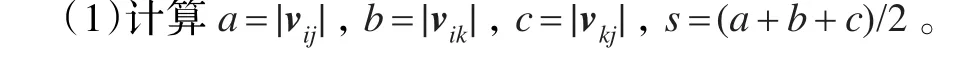
（2）采用三角形的性质来计算三角形内角的余切值。对于cotβij也按同样方法计算：

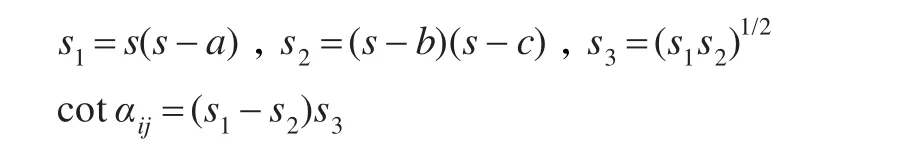
（3）采用公式（5）计算vj。

以上步骤共17m次实数乘法，2m次实数除法，4m次实数开平方（加减法计算量很小，实数乘除2的整数次幂可由位运算实现，故不考虑其计算量）。

3.2 平均曲率构造向量几何意义

首先分析平均曲率构造向量v的几何意义。把平均曲率计算公式中涉及的各个角度变换到一个三角网格内，如图3所示。

图3 Meyer法中各角度和向量变换示意图

比较图1和图3可知，v可改写为：

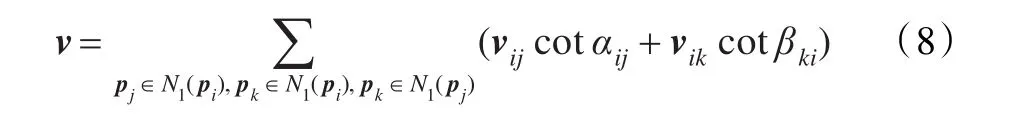
设

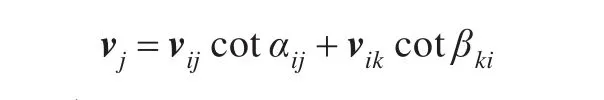
则有

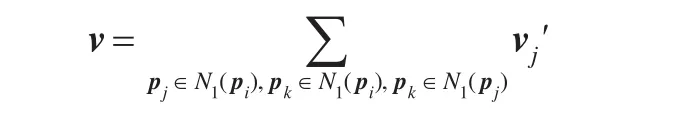
注意vj'与vj并不相同，但对于同一个v，求和号中vj'的数目与vj的数目是相等的，均为m。因为

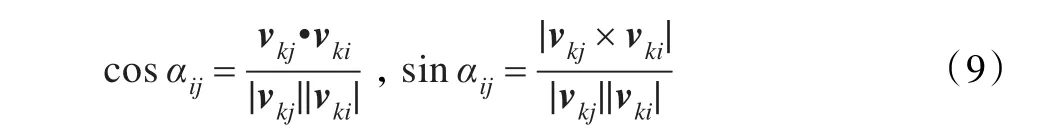
其中，vkj×vki表示向量vkj与vki的外积运算，并依此类推。所以

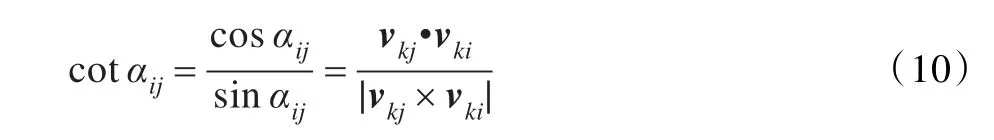
同理

如图4所示，在平面pipjpk内过点pi作直线pjpk的垂线pih，垂足为h。延长线段pih到h′，使得

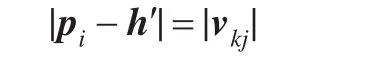
则有

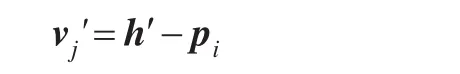
由此可见，v实际上是pi点的所有邻近三角面片中，pi点所在三角形的对边的正交向量的加权和，权值就是pi点对边的长度。这就是平均曲率构造向量v的几何意义。

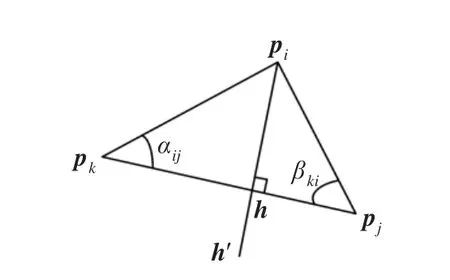
图4 vj'的几何意义示意图

3.3 平均曲率构造向量的改进算法分析

因而得改进算法步骤：

（1）计算

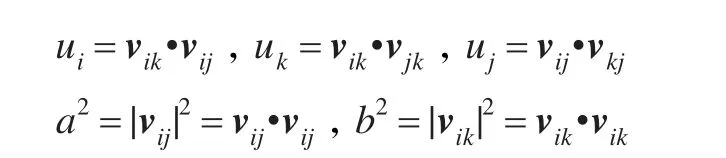
每2个相邻三角形有1条公共边，因而在N1(pi)内a2和b2的总计算量为3m次实数乘法。

（2）计算

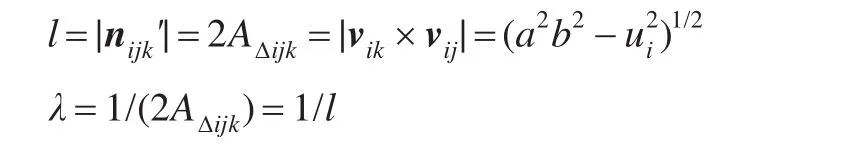
由公式（9）可得：

该步骤实际上附带得到了Δpipjpk的面积，可在后续的计算过程中使用。

（3）计算

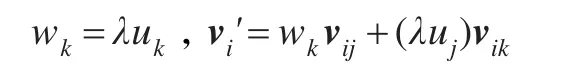
以上步骤共有22m次实数乘法，m次实数除法，m次实数开平方。

4 对Gauss曲率构造角的改进算法设计

4.1 Gauss曲率构造角的普通算法简述

通常，Gauss曲率构造角按如下步骤计算：

（1）对pi的每个直接邻近三角形（即有一个顶点为pi的三角形），根据下式计算角θ：

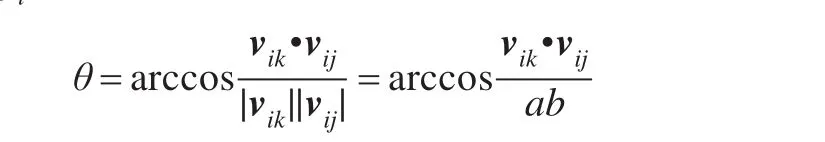
其中a和b在平均曲率构造向量的计算过程中已算出，不必重复计算。

（2）求和：

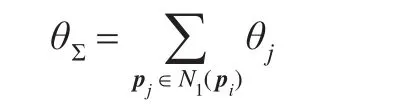
以上步骤共有4m次实数乘法，m次实数除法，m次实数反余弦运算。

4.2 Gauss曲率构造角的改进算法分析

利用了正切函数及两角和的正切公式，所得的改进算法步骤如下：

（1）对于pi的每个直接邻近三角形，计算cotθj的值（或θj=π/2）。根据公式（10）有：

（2）计算cotθΣ的值（或得到θΣ=(2r+1)π/2，r为非负整数），依次计算：

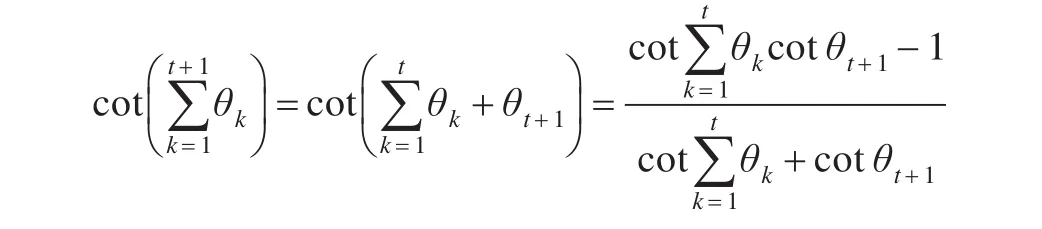
其中t的取值依次为1，2，…，m。注意须先处理分母为零的特殊情况，同时根据参与计算的两个余切值和所得结果的正负号，确定所得结果对应的角度所在的区间。最后得到cotθΣ=x。

（3）计算

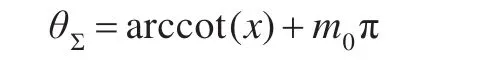
其中，m0为非负整数，由上述得到的θΣ所在的区间而确定。一般而言，m0的值不大，此处的m0π可用少数几次加法实现。

以上步骤共有2m次实数乘法，m次实数除法，1次实数反余切运算。

5 对混合面积的改进算法设计

5.1 混合面积普通算法简述

AΔijk一般可采用如下方法计算：

AΔijk，V的计算步骤如下：

（1）设Δpipjpk外接圆半径为R，则：

（2）计算图2中线段ohj和ohk的长度。

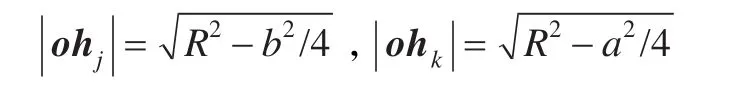
（3）计算面积AΔijk，V：

AΔijk，V=(a|ohj|+b|ohk|)/4

注意到在平均曲率构造向量的普通算法中，实际上已经计算出a2、b2、c2和。因而以上步骤共有5m次实数乘法，2m次实数开平方（假设所有三角面都是锐角三角形，下同）。

5.2 混合面积改进算法分析

如图5所示，连结pio并延长到点pm，使得pkpm||ohj，连结pkpm与pjpm。推导可得

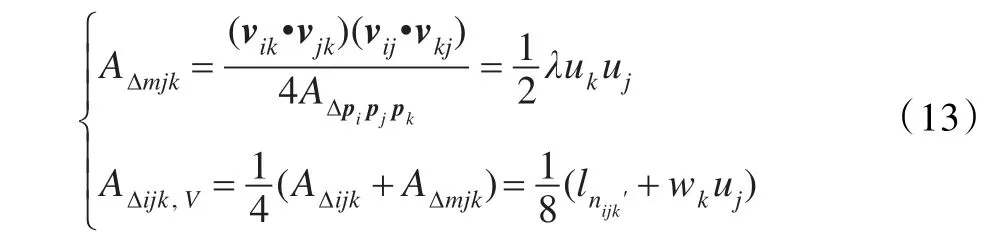
故共需m次实数乘法。

图5 Voronoi面积改进算法构造示意图

5.3 混合面积计算方法的判断

前文已提到，计算混合面积时，对不同的三角形，其计算方法不同。根据前述计算，有

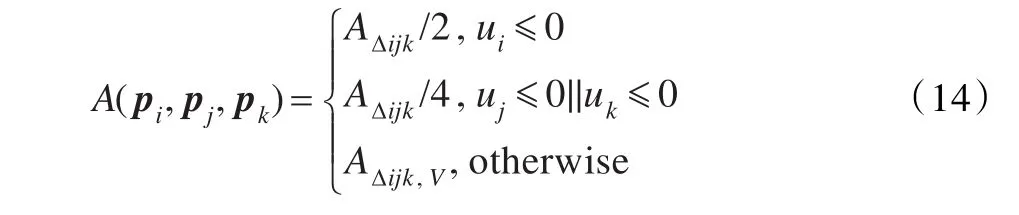
其中ui、uj和uk已在前述计算步骤中得到，因此对每个三角面片，决定采用哪种方法计算其混合面积时，并不需要额外的计算量。

综上所述，当所求点处的直接临近三角形全为锐角三角形时，普通算法共需26m次实数乘法，3m次实数除法，6m次实数开平方，m次实数反三角函数；而改进算法共需25m次实数乘法，2m次实数除法，m次实数开平方，1次实数反三角函数。

可见，改进算法中除了乘法次数与普通算法基本持平外，计算效率很低、耗时很长的除法、开平方和反三角函数的次数减少，因此提高了计算效率，同时更重要的是由于减少了计算量，避免了不必要的截断误差和舍入误差，从而有望减小计算误差，提高计算精度。

6 改进算法的效果

为验证所提算法的有效性，构造离散的椭球面、椭圆柱面、椭圆抛物面、双曲抛物面、双叶双曲面、单叶双曲面等6种离散标准二次曲面，分别按普通算法和所提改进算法计算对比。步骤如下：

（1）给定曲面形式、几何特征和空间范围，随机生成满足这些条件的离散点坐标及其三角网格拓扑结构，并计算各点处平均曲率和Gauss曲率的真实值。

（2）计算各点处的法向量真实值，在上述算法中的离散法向量均直接采用真实值，这样可避免采用离散算法计算法向量带来的误差。

（3）在同等计算条件下，分别采用普通方法和所提改进方法来实现M eyer算法，得到两种方法的相对误差（剔除因真实曲率为0而无法计算相对误差的点）；并记录两种算法所耗费的计算时间，得到计算精度和计算效率的评价。

采用的计算软硬件平台为：Intel®CoreTM2 Duo T5870@2.00 GHz CPU，4.00 GB内存，Window s 7操作系统，Visual C++2008开发平台。

曲率相对误差的统计直方图如图6所示。普通方法的平均曲率相对误差的均方根值为7.722%，Gauss曲率相对误差的均方根值为7.712%；改进方法平均曲率相对误差的均方根值为1.066%，Gauss曲率相对误差的均方根值为1.058%。

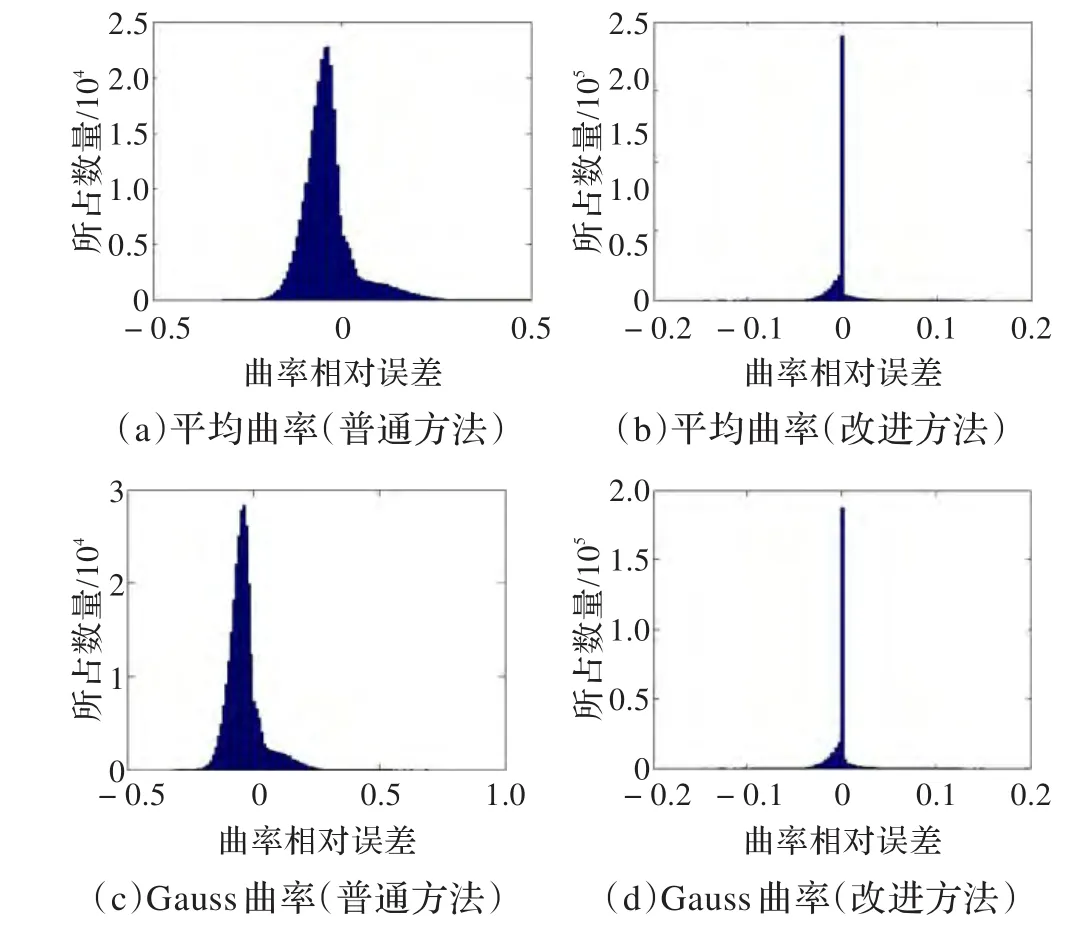
图6 计算精度对比（相对误差直方图）

对一个离散点的平均曲率与Gauss曲率的计算耗时的统计直方图，如图7所示。普通方法的耗时均方根值为1.222m s，改进方法耗时均方根值为1.036m s。

图7 计算效率对比（计算耗时直方图）

由计算结果可见，所提的改进方法大大提高了M eyer算法对离散平均曲率和Gauss曲率的计算精度，同时还提高了其计算效率。

7 结束语

通过分析M eyer所提的离散曲面一点处平均曲率和Gauss曲率的算法，提出了平均曲率构造向量和Gauss曲率构造角的概念，分析了其几何意义，并据此提出了提高计算精度和计算效率的改进算法。对6种典型离散标准二次曲面的仿真计算结果，表明了本文改进算法可大大提高曲率计算精度，同时还可提高计算效率。

[1]do Carmo M.Differential geometry of curves and surfaces[M].Englewood Cliffs，NJ：Prentice-Hall，1976.

[2]Chen Xin，Schmitt，F.Intrinsic surface properties from surface triangulation[C]//Proceedings of the European Conference on Computer Version.Heidelberg：Springer-Verlag，1992，588：739-743.

[3]Taubin G.Estimating the tensor of curvature of a surface from a polyhedral approximation[C]//Proceedings of the Fifth International Conference on Computer Vision.Piscataway，NJ：IEEE，1995：902-907.

[4]Meyer M，Desbrun M，Schröder P，et al.Discrete differential geometry operators for triangulated 2-Manifolds[J].Visualization and Mathematics，2003，3：35-57.

[5]Dong Chenshi，Wang Guozhao.Curvatures estimation on triangular mesh[J].Journal of Zhejiang University Science，2005，6A：128-136.

[6]Moreton H P，Sequin C H.Functional optimization for fair surface design[C]//Computer Graphics Proceedings，Annual Conference Series（ACM SIGGRAPH），Chicago，Illinois，1992：167-176.

[7]Chen S，Wu J.Estimating normal vectors and curvatures by centroid weights[J].Computer Aided Geometric Design，2004，21（5）：447-458.

[8]Page D L，Sun Y，Koschan A F，et al.Normal vector voting：crease detection and curvature estimation on large，noisy meshes[J].Graphical Models，2002，64（3/4）：199-229.

[9]柯映林，陈曦.基于4D Shepard曲面的点云曲率估算[J].浙江大学学报：工学版，2005，39（6）：761-764.

[10]方惠兰，王国瑾.三角网格曲面上离散曲率估算方法的比较与分析[J].计算机辅助设计与图形学学报，2005，17（11）：2500-2507.