景象匹配算法及其适应性分析

李竹林

延安大学计算机学院，陕西延安716000

1 引言

景象匹配技术是飞行器匹配定位辅助导航系统的核心，是利用飞行器装载的图像传感器在飞行过程中采集实时景象图，与预先制备的基准图进行实时匹配，计算出导航定位的相关信息[1]。但是由于成像时的天气、时间、空间等自然条件的变化，成像传感器和成像姿态差异等方面的原因，使得基准图与实时图之间存在着较大的差异，增大了匹配的难度。因此，如何提高景象匹配算法的正确匹配率、时间，以及算法的适应能力是研究景象匹配技术的热点与难点[2-3]。目前，国内外对景象匹配算法的研究表明，基于特征的景象匹配算法在景象匹配中效果较好[2，4]。但算法基本上是针对某一种应用而设计的，较为通用的匹配算法研究是该研究领域的难点之一。本文研究一种基于区域特征的景象匹配算法，充分考虑了景象匹配时图像的灰度、形状、纹理信息等因素的变化情况进行相似性度量，并对其匹配的时间、正确匹配率以及适应性做了大量的仿真实验与分析。结果表明，算法效率较高，适应性较好。

2 区域特征提取

在景象匹配中，所关心的并不是实时图和基准图中所有的像素的对应关系，而是判断图像中是否包含的打击目标。因此，通常对基准图中已提取的区域首先进行人工交互判别，对有意义的标志性区域作标记。这样，景象匹配时，在实时图中只寻找对应的区域即可。所以，基于区域特征的匹配算法比基于特征点的算法更适合景象匹配，而且区域特征比点特征包含更多的信息，可区分性强，可以大大提高匹配的速度和正确匹配率。根据景象匹配技术的需求，文中对M atas[5]提出的MSER算法进行研究应用。

M atas提出了稳定极值区域（M aximally Stable Extrema Regions，MSER）提取算法，其思想是所提取的最大稳定极值区域内的所有像素亮度比区域边界外的像素高，或者比区域边界外的像素低。

设景象图片的像素值为I(i，j)，若

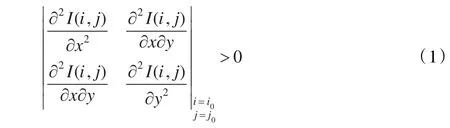
则I在(i0，j0)处取得极值，且当0时，取极小值；当0时，取极大值。

3 景象匹配算法

在前视制导方式下，弹载终端在时间t内，对地形或目标进行拍摄形成实时序列图，来表征目标的影像。其中序列影像的拍摄时间间隔Δt足够小。按照序列影像的先后时序与预先装载的基准图进行匹配，当重叠区域大于90%以上时，认为匹配成功。

3.1 区域属性描述

（1）平均灰度与方差。设M×N区域的平均灰度与方差分别为表达式（2）与（3）[1，6]：

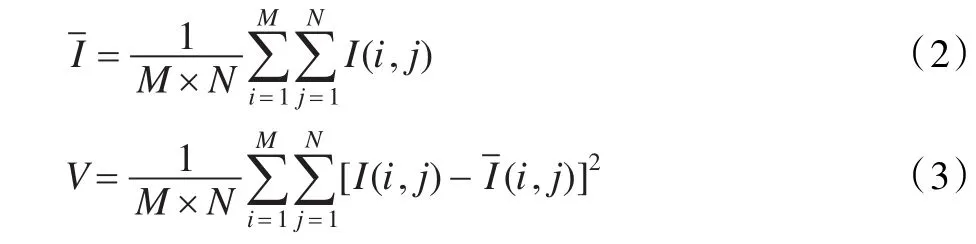
其中，I(i，j)为像素点(i，j)的灰度值；方差V反映了区域总的起伏程度。

（2）仿射不变矩。给定离散化的数字图像f(x，y)，其p+q阶矩定义为：

将一阶矩用零阶矩归一化后即得到目标区域的灰度质心坐标为：

以灰度质心为坐标原点的矩称为中心矩，即

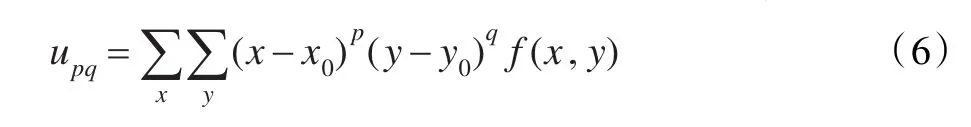
为了使中心矩不随比例缩放而变，进行归一化处理，可以得到归一化的不变矩为：

式（7）中，r=(p+q)/2，p+q=2，3，…。

Jan Flusser用不大于三阶的矩构造了3个不变矩组[7]：

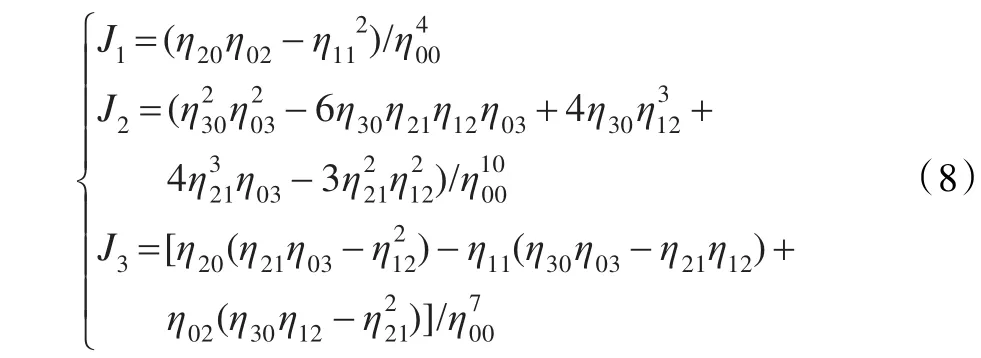
大量实验表明，仿射不变矩在图像发生仿射变换的情况下，仍可清晰地表征图像特性，因此利用仿射不变矩可以识别形状发生变化的局部区域。

（3）纹理信息熵。设区域中相距位置为(Δx，Δy)，且其灰度值差的绝对值|h-k|的像对出现的次数记为mkk，其熵信息可以表示为[8]：

用公式（9）计算已确定的初始对应区域的纹理信息熵。熵的绝对值越大，图像所含信息也越多，就越有利于匹配，反之则不利于匹配。

综上四方面的区域特征描述，即区域灰度、区域总的起伏程度、区域形状以及区域纹理，作为景象匹配时的主要决定因素，增强匹配的适应性与准确性，提高了匹配的正确率。

3.2 相似性度量函数

在景象匹配中，灰度信息、方差、仿射不变矩以及纹理信息熵等6个属性值构成区域的特征矢量λ={，V，J1，J2，J3，fENT}用于度量区域的相似性，而距离法是度量两个矢量最简洁有效的方法。Hausdorff距离是匹配点特征的一种方法，它不需要建立点之间的一一对应关系，只是计算两个点集之间的相似程度（最大距离），所以可以有效地处理很多特征点的情况[8-9]。本文的匹配基元是区域，为了提高匹配的准确性，计算了区域的6个属性变量，可作为Hausdorff相似性度量的点集。因此选择Hausdorff距离作为度量方法可以提高匹配正确率与实时性。

给定两个有限点集A={a1，a2，…，ap}和B={b1，b2，…，bq}，则A、B间的Hausdorff距离H(A，B)定义为：

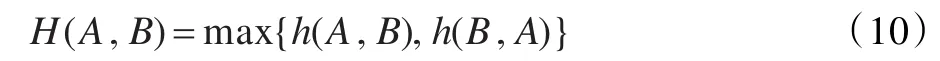
其中，h(A，B)和h(B，A)分别为A→B与B→A的有向Hausdorff距离，定义为：

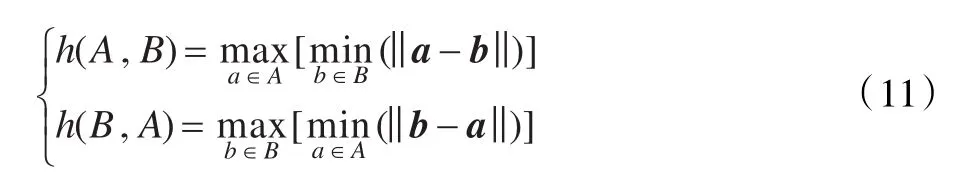
其中符号‖·‖为定义在点集A和B上的某种距离范数，比如欧氏距离。

3.3 匹配算法描述

（1）基准图的处理步骤

步骤1 对基准图进行去噪、增强、剪裁等预处理。

步骤2 用MSER算法检测基准图的稳定极值区域，作为特征区域。

步骤3 通过人机交互的方式，对具有标志性的区域作标记。

步骤4 计算基准图中已标记区域的特征矢量λ={V，J1，J2，J3，fENT}。

（2）景象匹配算法步骤

步骤1 用MSER算法检测出实时图中的稳定极值区域，作为特征区域。

步骤2 计算实时图中检测到的区域特征矢量λ′={'1，V，J′1，J′2，J′3，f′ENT}。

步骤3 计算H(A，B)的值，用Hausdorff距离法实现实时图与基准图间的匹配。

步骤4 若H＜δ（δ为给定的阈值），则说明匹配成功，则转步骤5；否则，若实时图序列不为空，则取下一张实时图像，重新执行步骤1～步骤4。

步骤5 结束。

4 实验结果及适应性分析

在仿真实验的过程中，为了计算简单，取基准图大小为640像素×640像素，实时图大小为160像素×160像素。

4.1 模拟实验结果

对图1（a）～（c）中的示例图进行模拟实验，其中，基准图中的5个标志性区域，如图2（f）所示，它们属性值的实验数据见表1所示，表2给出景象匹配的正确率。

表1 基准图中标记区域的属性值

表2 图像匹配结果

在该实验结果中，由于不变矩的值较大，根据经验值，给定的Hausdorff距离阈值为25，其最佳匹配平均时间可达到0.138 s，最差为0.64 s；最佳正确匹配率为92.67%，满足了前视景象匹配的基本要求[1]。

4.2 算法适应性分析

下面就常发生的一些变换及噪声情况下算法的适应性能力进行实验。以下几种情况所用图像为同一组，每种情况实验次数为100次，然后取平均值。

（1）噪声情况

图像的信噪比是衡量图像质量的一个重要参数，也是景象匹配中描述噪声干扰大小的重要手段。设大小为M×N的原始图像为X(m，n)，-X(m，n)为原始图像的均值图像，含噪声重构图像为X′(m，n)，则图像的信噪比[10]定义为：

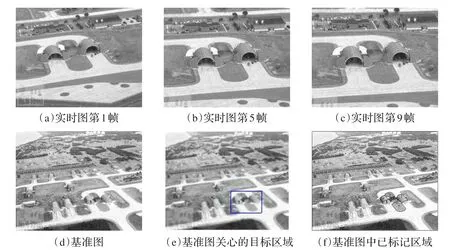
图1 实时图序列和基准图

由于信噪比不是线性属性，为了方便，本文采用加噪级数来代替信噪比，每一级噪声对应其相应的信噪比值。下面选高斯噪声和椒盐噪声这两种典型而常见的噪声模型进行分析。

①高斯噪声。高斯噪声匹配数据如表3（表中平均匹配时间为416.23ms）。数据的采集方法：每一级高斯噪声均值为0，方差为0.1。

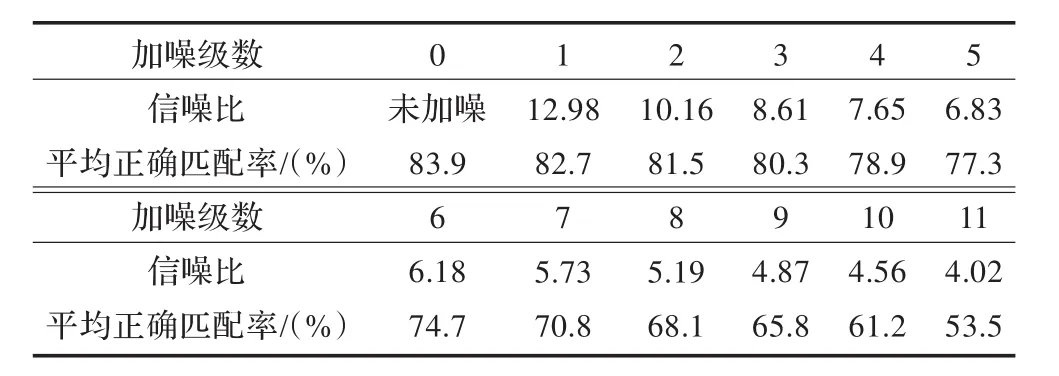
表3 算法在高斯噪声下的匹配数据

②椒盐噪声。椒盐噪声匹配数据如表4（表中平均匹配时间为592.38m s）。数据的采集条件与高斯噪声情况基本相同，只不过每一级高斯噪声换成了强度为0.005的椒盐噪声。

表4 算法在椒盐噪声下的匹配数据

从整体上看，该算法的抗噪能力较强，但在椒盐噪声下的正确匹配率较高斯噪声有所提高。当噪声级数小于5的时候，算法的稳定性非常好。

（2）几何畸变情况

由于巡航导弹在空中的飞行姿态是不断变化的，如爬升、俯冲、侧翻等，这就引起弹上获取实时图的光学系统的视角不断变化，最终造成实时图存在各种几何畸变。本文选取三种典型的几何畸变进行分析。

①旋转失真。旋转失真匹配仿真试验数据见表5（表中平均匹配时间为546.37ms）。

表5 算法在旋转失真下的匹配数据

从表中数据可以看出，随着旋转角度的增加，即畸变幅度的增大，各算法的匹配正确匹配概率降低。但是由于算法的相似性度量时，不仅仅采用灰度相关法，而且考虑到区域的形状信息和纹理信息，因此，对于旋转变化，当旋转的角度不是很大时，算法的适应性较好。

②扭曲失真。匹配仿真试验数据见表6（表中平均匹配时间为582.76m s）。

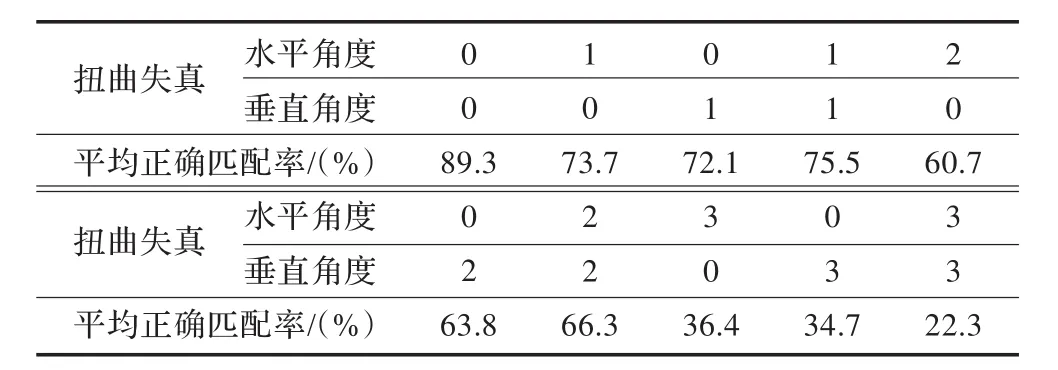
表6 算法在扭曲失真下的匹配数据

从匹配数据上看，当形状发生了严重的畸变时，算法对扭曲失真的适应性不好。

③比例失真。图像是发生均匀比例变换，匹配仿真试验数据见表7（表中平均匹配时间为462.15ms）。

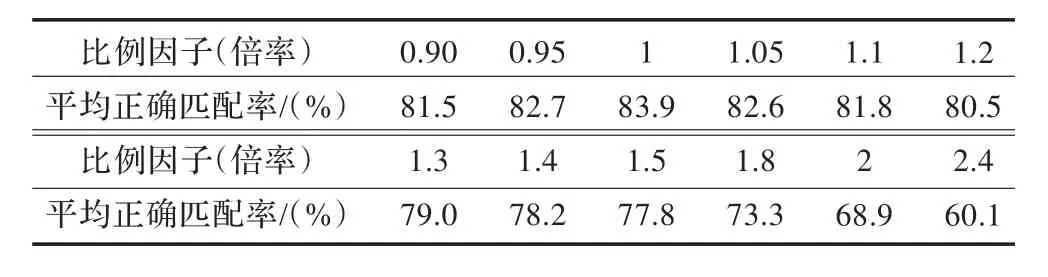
表7 算法在比例失真下的匹配数据

从匹配数据上看，算法对比例失真的适应性较好，这是由于比例失真只是图像的相似性变换，只要相似性度量算法合理，匹配效率就可能基本保持。

（3）灰度畸变情况。

由于各种天候的影响，如晴天、阴天、雨、雪、雾等，容易造成预先获得的基准图与巡航导弹实时摄取的实时图发生整体灰度上的差异，这些差异主要存在于图像的亮度、对比度等。

①亮度失真。亮度失真的匹配数据见表8（表中平均匹配时间为497.54m s）。

表8 算法在亮度失真下的匹配数据

表8中，亮度变化单位lx为勒克司，1 lx=1 lm/m2。

从匹配数据上看，随着亮度的变化，匹配的性能迅速下降。这也是基于灰度特性的匹配算法的面临的一大难题。

②对比度失真。对比度范围从0.58变化至1.80。表9所示为匹配实验数据（表中平均匹配时间为550.78ms）。

如果对比度小于1.00，且越变越小时，图像像素是亮的变暗，暗的变亮。因此随着对比度的降低，正确的匹配率也随之而降。特别是，当对比小于0.70时，由于图像灰度过于集中，使图像特征变得模糊，匹配概率会很低。当对比度大于1.00且越变越大时，图像像素是亮的变得更亮，暗的变得更暗，且各像素变化幅度是相同的。因此，在较高对比度情况下，正确的匹配率基本上不受影响，反而会因为对比度适中匹配效果增强。

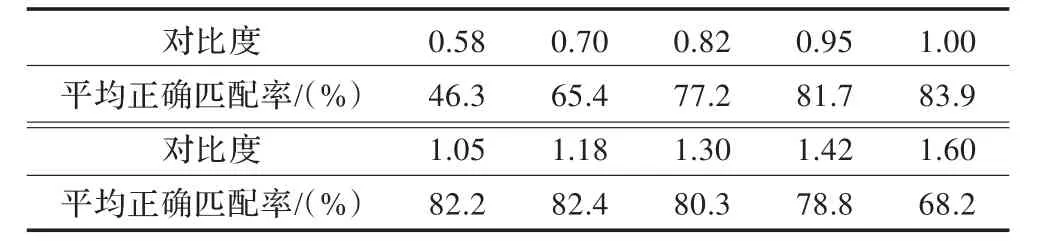
表9 算法在对比失真下的匹配数据

综合上述分析，可以看出，本文的景象匹配算法总体的适应性良好。特别是对旋转、尺度、噪声、灰度变化的适应性较好。但是对于形状发生扭曲、对比度严重失真，以及亮度变换非常大的情况，适应性不好。

5 结束语

提出一种基于区域特征的景象匹配的算法，利用区域的灰度、形状、纹理以及起伏程度特性，构造了相似性度量函数，解决了实时景象与基准图景象的区域块匹配问题。模拟实验和算法适应性分析表明，该方法的正确匹配率与平均匹配时间均可达到要求，且对旋转、尺度、噪声、灰度变化的适应性较好。因此，本文算法对景象匹配具有重要的参考价值。

[1]曹菲.景象匹配制导基准图选定准则研究[D].西安：第二炮兵工程学院，2006.

[2]郭勤.景象匹配技术发展概述[J].红外与激光工程，2007，36（S2）：57-61.

[3]王刚，段晓君，王正明.基于图像区域相关的景象匹配概率与精度研究[J].宇航学报，2009，30（3）：1237-1242.

[4]李竹林.立体匹配技术研究及其在导弹精确制导中的应用[D].西安：第二炮兵工程学院，2008.

[5]Matas J，Chum O，Urban M，et al.Robust wide baseline stereo from maximally stable extremal regions[J].Image and Vision Computing，2004，22（10）：761-767.

[6]孙即详.图像分析[M].北京：科学出版社，2005.

[7]Flusser J，Suk T.Pattern recognition by affine moment invariants[J].Pattern Recognition，1993，26（1）：167-174.

[8]Yang C H，Lai S H，Chang L W.Reliable image matching via modified Hausdorff distance with normalized gradient consistency measure[C]//Proc of International Conf Information Technology：Research and Education，Hsinchu，Taiwan，China，2005：158-161.

[9]牛力丕，毛士艺，陈炜.基于Hausdorff距离的图像配准研究[J].电子与信息学报，2007，29（1）：35-38.

[10]Gonzalez R C，Woods R E.Digital image processing[M].2nd ed.[S.l.]：Prentice Hall，2002.