综合预测模型的构建及预测系统开发研究

何超，刘西林

西北工业大学管理学院，西安710129

1 引言

预测精度不仅与所用数据有关，还与选用的模型有关。预测科学发展至今，已积累了许多行之有效的预测方法，据不完全统计，多达300种[1]。传统的单个预测模型仅是从模型提前假设好的某一方面表示数据规律，通常丢失了大量隐藏在数据中的信息，具有片面性。组合预测（也称综合或复合预测）[2]是一种利用各单项预测得到的预测信息，计算给予不同的权数组合，以获得组合预测值的预测方法。Bates和Granger[3]在1959年首次提出组合预测理论，1969年，Bates和Granger在“运筹学季报”发表“组合预测”[4]，对仅仅是两个预测结果的组合进行了系统研究。对于常见的时间序列，有研究表明，没有哪一种方法能适用于所有的时间序列预测，而应根据实际情况，选择适当的模型与方法[5-6]。国内在20世纪80年代中后期关于组合预测也有一些研究成果，而大部分组合预测[7-14]也都仅是两种方法的组合。通过相关文献检索，发现现有组合预测模型还存在以下不足：（1）组合的兼容性与可增加性。已有的组合方法基本上都是将两种预测方法组合起来，涵盖的范围较窄，一般不能够在组合中再加入第三种预测方法。（2）预测方法与系统结合的不紧密。若能够实现预测方法与系统的结合，将使得预测自动化，这有利于科研成果走进企业应用，实现科研成果的迅速推广。

针对此，本文构建了一般的组合模型，并且从多元线性回归的角度给出权系数的数学计算步骤，避免人工赋权、专家难寻的弊端，使得模型具有可添加性。在此基础上，建立专门的投资预测系统，实现预测的自动化，这使得科研成果能被实际企业应用。

2 综合模型的构建与求解

2.1 综合预测模型的构思

本文构建的综合预测模型试图将多种预测方法得到的预测结果进行组合，使最终的预测结果具有更高的精度。预测精度衡量的标准是最小方差，即将多种预测方法得到的预测值进行加权组合后得到的综合预测值与给出的原始数据之间误差的平方和最小。转化为数学模型为：

式中，x1，x2，…，xp表示p种不同的预测方法计算的预测结果；β1，β2，…，βp则表示p种预测方法各自的权系数。

同时，为了使结果能更加体现各个预测方法在综合模型中的相对重要程度，还需满足条件：

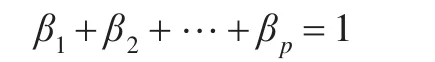
只有满足上述两个条件的β1，β2，…，βp即综合模型所要求的权系数。

2.2 综合预测模型的求解

2.2.1 综合预测模型目标函数的求解

函数：

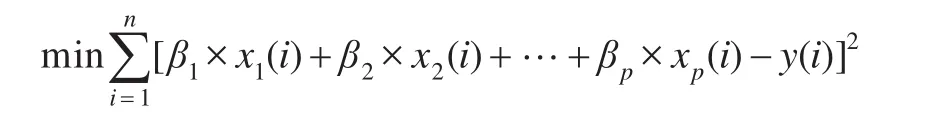
在形式上与p元线性回归方程

相似，本文就是试图利用多元线性回归模型来求解权重β1，β2，…，βp。

从模型意义角度上讲，多元线性回归研究的是因变量与自变量间的因果关系，而综合预测模型与所选取的典型模型方法之间也存在因果关系，典型预测方法的预测结果是影响综合预测结果的因素。

基于此两点，本文建模的求解过程利用了多元线性回归模型的思路。

假设影响结果y的因素有p个：x1，x2，…，xp。假设它们之间有线性关系：

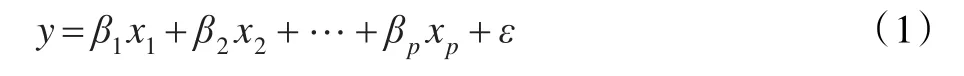
式中x1，x2，…，xp都是可精确测量或可控制的一般变量，y是可观测的随机变量，β1，β2，…，βp是未知参数，ε是服从N(0，σ2)分布的随机误差。对于n组样本

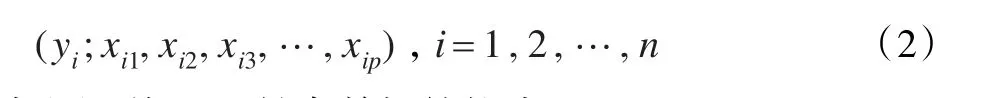
由式（1）可知，yi具有数据结构式：

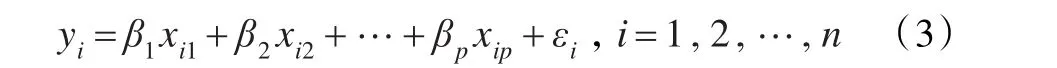
其中各εi(i=1，2，…，n)相互独立，且均服从N(0，σ2)。的估计分别记为那么得到一个p元线性方程：

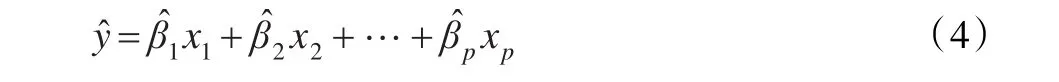
将样本点式（2）代入式（4），可求得相应的值

想要求出β1，β2，…，βp的估计值，使得由式（5）计算得的与yi之间的离差最小。

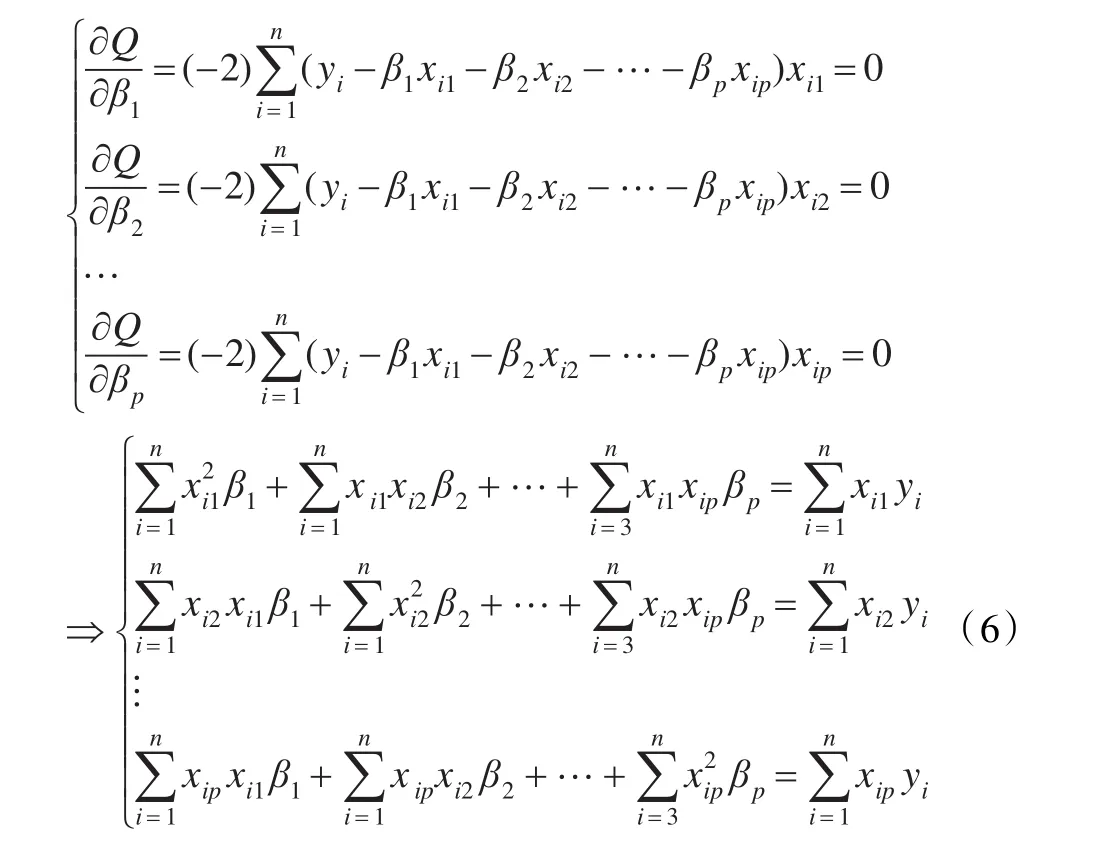
其解β1，β2，…，βp称为最小二乘估计。

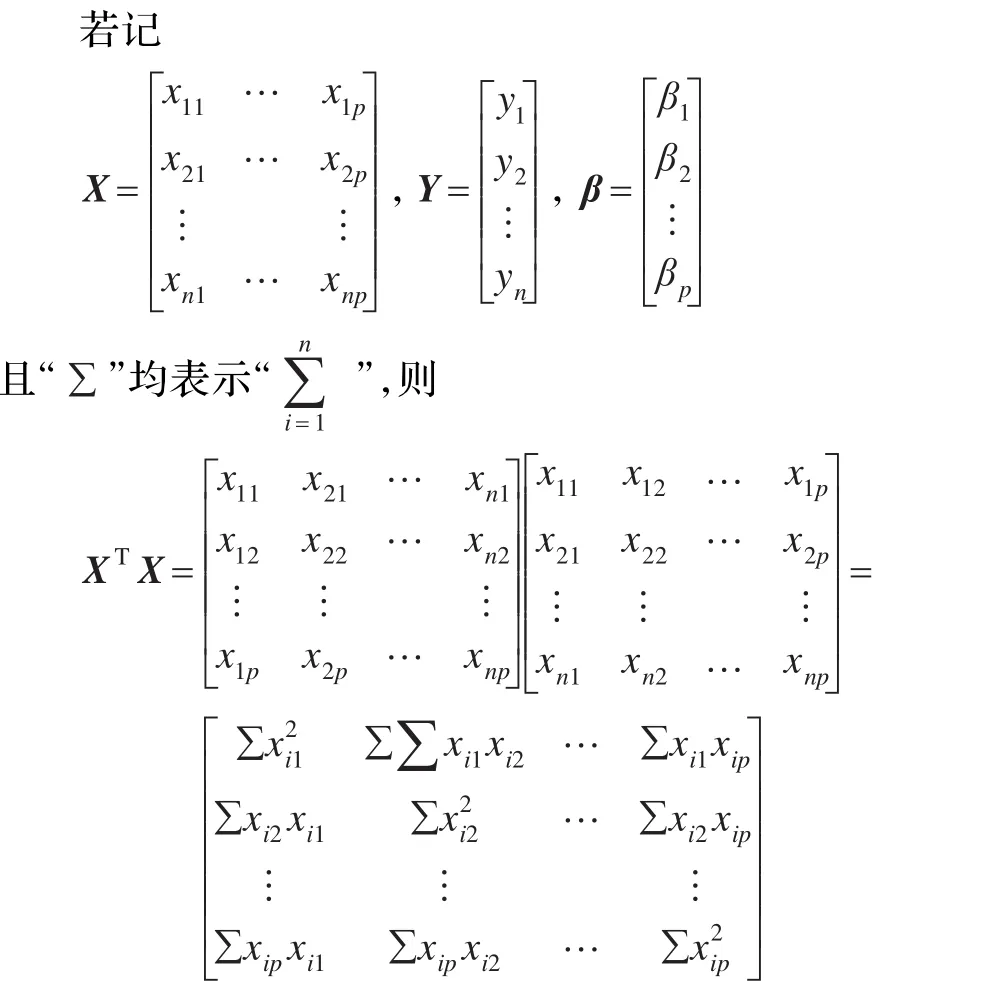
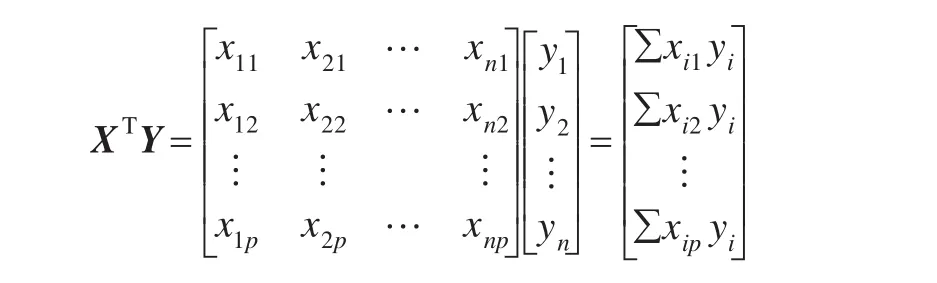
因而式（6）用矩阵形式可简洁地表示为：

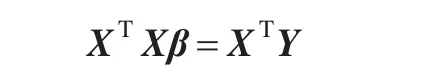
在回归分析中通常(XTX)-1存在，从而最小二乘估计可表示为：

借助多元线性回归的思路完成了β1，β2，…，βp的估计值，使得由式（5）计算得的与yi之间的离差最小。

2.2.2 综合预测模型中约束求解的探索

建模中的第二步，使得权值之和为1，即满足

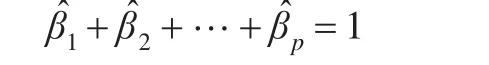
穷举法：借助MATLAB强大的计算能力，但在实际操作过程中会遇到很多问题。如：穷举法的取值间隔不好把握，间隔不可能取到足够小，而取得较大可能导致错过极值点。实验表明，当选取的间隔较小，达到小数点后4位时，穷举法就会有非常大的计算量，导致MATLAB卡死；更重要的是，综合预测模型是选取多种合适的预测方法进行组合，随着更多合适的预测方法被发现，加入到综合模型中的方法越多，使用穷举法的计算量就会大幅上升，用这种方法解决的缺陷就更加明显。

同样借助回归分析思路，可求得权值。但是回归分析的思路过程中，本身不涉及权值和为1这样的条件，若要满足权值和为1，只能通过外部加入。从这样的指导思想出发，设想在外部引入和为1这样一个条件。已知β1，β2，…，βp，如果存在第βp+1种预测方法，则βp+1就应当满足

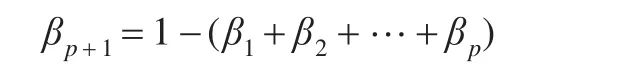
通过这个方程，并经过多次的实验推理后，本文将该函数作为已知条件来解决。具体来讲，已知线性关系：

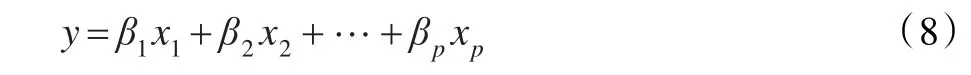
等式约束为：

将式（9）代入到式（8）中，得到：

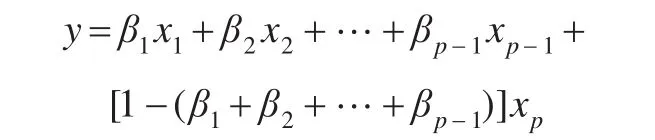
化简得：

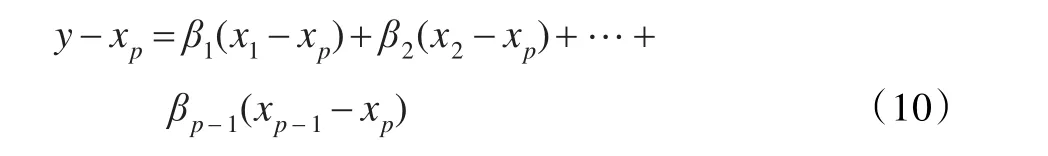
将(y-xp)记为z，将(xi-xp)记为mi，其中i=1，2，…，p-1。

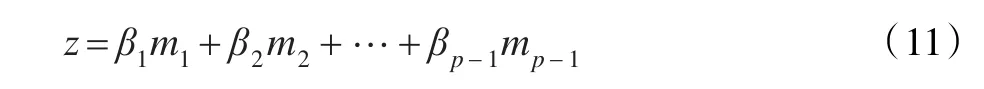
则式（10）可写为：这个式子与p-1元线性回归方程很类似，这时运用上节提供的思路，由式（7）

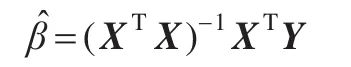
同理推导出来式（11）最小二乘估计：

其中，M=[m1m2m3…mp-1]，Z=[y-xp]n×1。

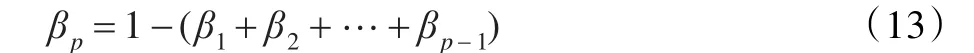
可知βi的估计值也满足：

至此，满足本文最初建模要求

的p种预测模型的权重β1，β2，…，βp完满求得。

3 实例验证

投资预测及决策是油田开发生产企业经济管理的首要环节，合理安排投资规模是保证油田经济稳定发展的基础，投资增长过猛，规模过大，超过资金供给的可能，会给油田经济带来严重的消极后果。一般油田企业在确定某油田有持续开采的经济价值后，需要连续投资。

现以某油田1998年—2007年勘探开发投资规模为例来验证本文提出综合预测模型的正确性。通过对多个单一模型各自使用条件与实际预测结果多次用MATLAB软件仿真比较后，最终选用移动平均法（2阶）、多项式拟合法（4阶）、指数函数法、灰色预测模型作为四种独立的方法对投资规模进行预测（这四种方法的理论在文献[15]中）。在此基础上，完成综合预测模型。

3.1 综合预测模型的计算及M ATLAB软件仿真

综合最优模型所需要用到的是上一章中推导出的四个式子：

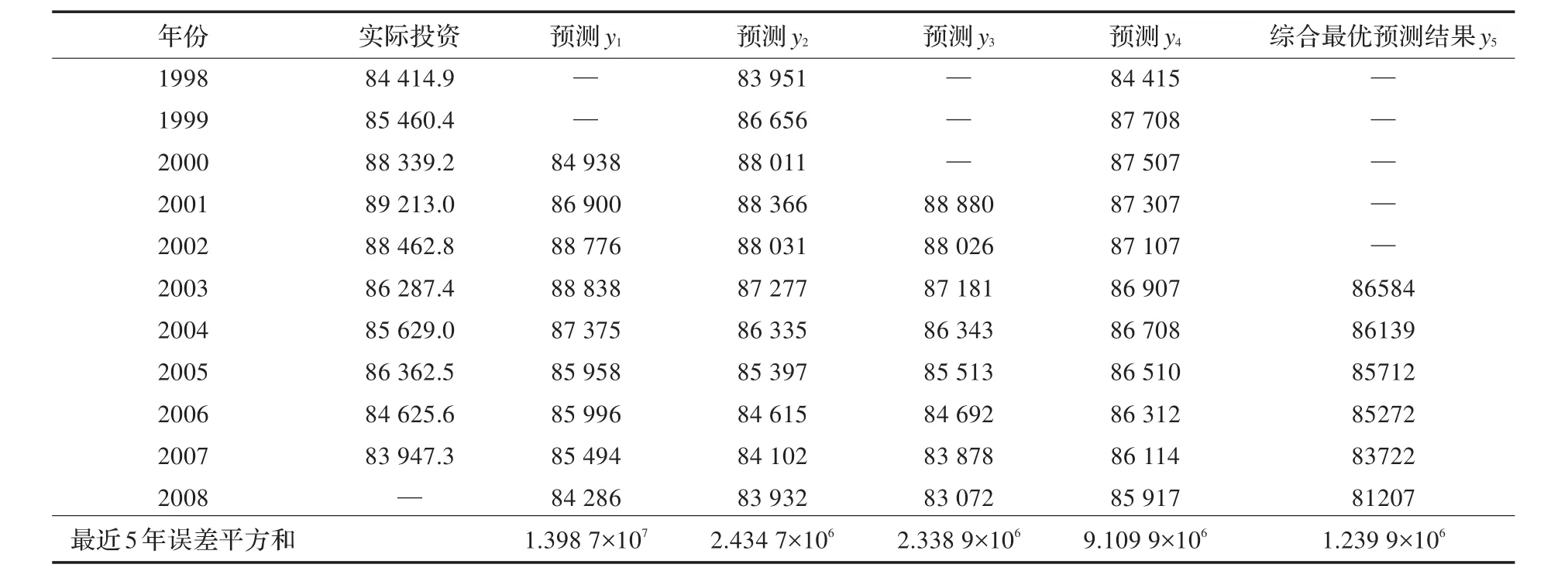
表1 单个模型及综合模型预测结果

利用上一节的结论计算权重。

各单一预测方法及综合预测模型预测结果如表1所示。其中：

y1表示移动平均法（二阶）模型预测结果；

y2表示多项式拟合法（四阶）模型预测结果；

y3表示指数函数模型预测结果；

y4表示灰色预测模型预测结果；

y5表示综合模型预测结果。

从表1结果可看出，组合后的预测结果y5，其误差平方和最小，达到了最初建立综合模型的目的。

用MATLAB软件仿真得各个预测结果趋势图，如图1所示；将2003年—2008年的图像进行放大观察，如图2所示。由图可看出，综合预测模型趋势线对于数据点的拟合情况相比单一的四种预测结果都要好，由此可判断组合后的预测结果精度有所提高，预测结果更可靠。

图1 单个模型及综合最优模型趋势图

综合预测结果可表示为：y5=a×y1+b×y2+c×y3+d×y4。

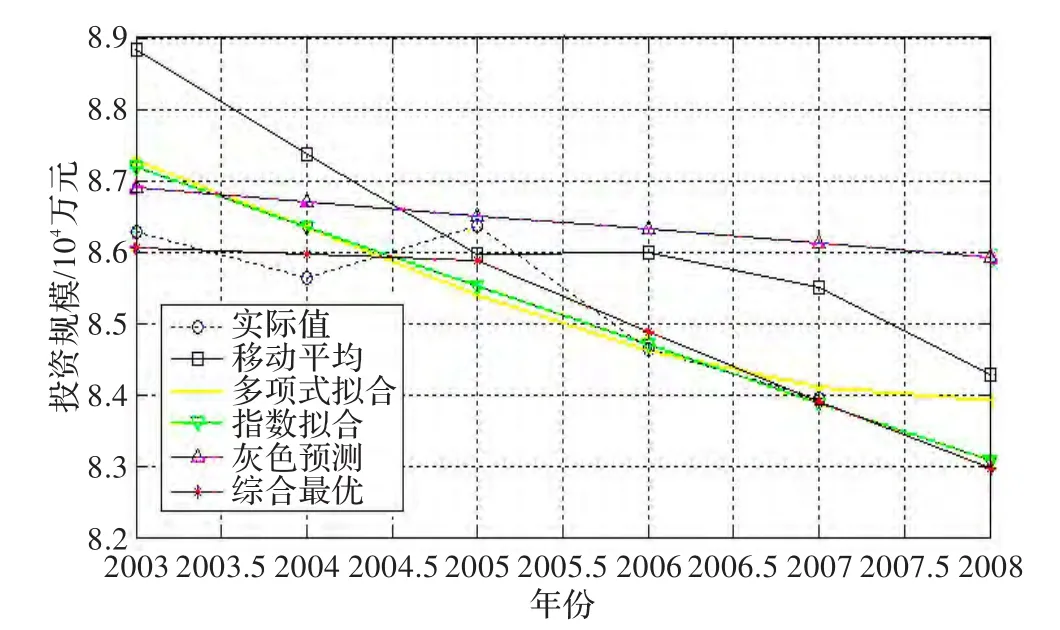
图2 放大的单个模型及综合模型趋势图

计算得到的各权重：a=-0.539 1，b=-0.997 5，c=2.039 1，d=0.497 6。

由表1还可看出四种单一预测模型中指数模型的误差平法和最小，指数模型在综合模型中所占的权重也的确是最大的。这符合常理，预测精度高的模型在综合模型中的权重也会较大。而且从表中结果可以看出，综合后的预测结果y5，其误差平方和最小，达到建立综合模型的目的。

3.2 综合预测系统

初始数据不同，选用拟合方法的不同，都需要重新建模，重新仿真。为了避免重复建模与实现预测的自动化，本文针对上例建立了专门的预测系统，使得预测简单化、自动化，视图直观化。该系统的建立，使得对预测模型不懂的非专业人员也能利用此系统进行预测计算，方便决策者做出决策。此处为说明问题，只简要展示了用户认证模块与数据综合处理模块，如图3～图5，在实际应用中，企业可以根据自身情况，建立更加完善的系统，作为企业内部使用。

3.2.1 登陆模块

登陆模块如图3、图4所示。

图3 登录界面

图4 提示窗口

图5 组合处理模块界面

3.2.2 综合处理模块

各个单独模型及综合模型处理的结果如图5所示，决策者可根据综合预测结果为决策依据，做出投资规模决策。

4 结论

以往的组合预测仅仅是建模、计算，并且主观的人工赋权会直接影响到预测的准确性，而本文建立的通用综合预测模型，不仅从多元线性回归的角度给出权系数的数学计算步骤，而且增加了组合预测模型的可添加性。通过实例验证了本文模型及计算步骤的正确性，并建立了专门的投资预测系统，将预测与系统紧密结合，使得预测自动化，有利于科研成果走进企业应用。

[1]冯文权，茅奇，周毓萍.经济预测与决策技术[M].4版.武汉：武汉大学出版社，2002.

[2]陈春光.组合预测在石油行业预算管理中的应用[D].天津：天津大学，2008：55.

[3]商勇，丁咏梅.最优组合预测方法评述[J].统计与决策，2005（9）.

[4]Bates JM，Granger CW J，The combination of forecasts[J].Operational Research Quarterly，1969，20：451-468.

[5]Dantzig G B，Ramser JH.The truck dispatching problem[J].M anagement Science，1959，10（6）：80-91.

[6]Laporte G，Nobert Y.A branch and bound algorithm for the capacitated vehicle routing problem[J].Operations Research Spektrum，1983，5：77-85.

[7]石慧，王玉兰，翁福利.BP神经网络和模糊时间序列组合预测模型及其应用[J].计算机应用，2011（A 02）：90-91.

[8]戴荣，黄成.飞机飞行事故率预测建模与仿真研究[J].计算机仿真，2011，28（7）：120-123.

[9]刘东君，邹志红.灰色和神经网络组合模型在水质预测中的应用[J].系统工程，2011-09.

[10]鲍单，吴艳萍，何勇.基于GM（1，1）模型和线性回归的组合预测新方法[J].系统工程理论与实践，2004（3）：95-98.

[11]张倩，沈利，蔡焕杰，等.基于灰色理论和回归分析的需水量组合预测研究[J].西北农林科技大学学报：自然科学版，2010，38（8）：223-227.

[12]侯丽敏，马国锋.基于灰色线性回归组合模型铁路客运量预测[J].计算机仿真，2011（7）：1-3.

[13]甘健胜，陈国龙.线性组合预测模型及其应用[J].计算机科学，2006，33（9）：191-194.

[14]许秀莉，罗健.一种新的组合灰色神经网络预测模型[J].厦门大学学报，2002（3）：164-167.

[15]刘思峰，党耀国.预测方法与技术[M].北京：高等教育出版社，2005-08.