含有高阶微分项引力场的自由传播子的计算

明 钢，邵 亮，秦正辉，李 苗，代 熠

（武汉科技大学理学院，武汉430065）

1 符号和记号

引力量子化大体有两种途径.一种是利用引入其它场、延展体、超对称等方法，企图使引力量子化.这些方法中除超弦M－理论外，其余皆因解决可重整性问题无望而无法发展.而M－理论中，关于引力相互作用的核心问题，目前也欠全面和具体的阐明，完成引力的最终量子化，还需长期的过程.另一种是，在引力体制内进行引力的量子化.这种方法历史上提出的具体模式很多，其中最被推崇的是4－导数引力.这种理论是把广义相对论中的微分同胚变换当作规范变换［1］，将模式中的引力场用Faddeev规范场量子化的方式量子化.其优点是可以用（引力）曲率平方项的引入消去引力的发散，理论在表现上具有可重整性.它需要解决的问题是，理论中存在负能量的粒子；若解决负能量问题，可能破坏S矩阵的么正性.尽管如此，这一理论仍是协变方法实现引力量子化进行得最为彻底的一种理论.这一方法在引力量子化历史上曾引起不小的关注，如，Rovelli在文献［2］中回顾引力量子化简史时，曾例举过对Stelle提出的4－导数引力量子化的评述［3］.它指出，尽管4－导数引力存在需要进一步解决的问题，它曾仍被认为是解决量子引力问题的一种可行选择.Gambini和Pullin在文献［4］中谈到引力量子化的可重整性时，也指出了4－导数引力在作用量中引入高次项的方法可以用于治疗引力发散，不过应当去掉它为理论带来的非物理性质.

在微扰量子引力中，协变量子化是应用较多的一种方法.它借助路径积分法研究Einstein引力及其修正理论的量子化传播子的重整化在现代物理中也是一个相当重要的问题.自上世纪初建立量子场论以来，量子场论一直是描述微观高能粒子相互作用的成功理论与有效计算方法.采用微扰理论作低阶（树图）微扰计算较为容易，且不出现“发散”困难；但作高阶（圈图）微扰计算时，将出现“发散”困难.虽然重整化理论能合理消除“发散”，但由此出现的重整化计算问题又将导致理论计算处理上的异常困难.重整化的计算可以分离掉高阶（圈图）计算中非物理“发散量”，而保留所需的物理“有限量”.在许多重要物理问题的深入研究中，尤其需要考虑并寻求至少单圈图计算中的重整化“有限量”，其贡献（辐射修正）虽然十分微小，但在理论的精确描述意义上却显得非常重要.由于重整化计算的重要性以及理论计算上出现的复杂性，致使重整化计算问题研究一直备受学术界关注.然而对于重整化问题作具体理论计算时，至今采用较多的仍然是针对具体物理问题作某些近似考虑后建立的各种近似理论与方法.本文将以引力场的自由传播子为中心，对携有高阶微分项的引力的自由传播子进行微扰计算.

以下对本文使用的符号和记号加以归纳，在Minkowski时空里，协变度规张量密度定义为：

协变度规张量gμν（x）展开为：

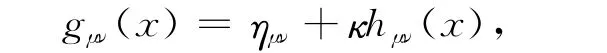
逆变度规张量gμν（x）展开为

其中，ημν是Minkowski背景的度规，hμν（x）代表其在真空中传播的引力子.

逆变度规张量密度g～μν展开为：

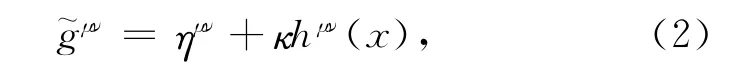
协变度规张量密度g～μν展开为：

2 R＋R 2＋RμνRμν－引力的作用量的引力场hμν展开

N维Minkowski时空中的R＋R2＋RμνRμν－引力作用量为：

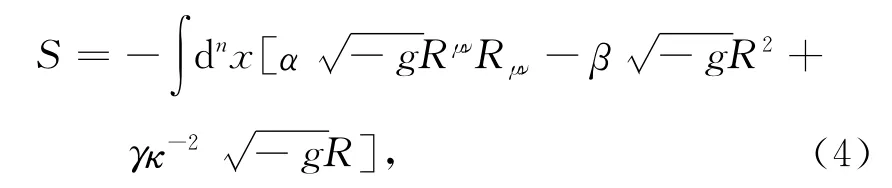
式中，α，β，γ为常数.将（1）式代入Christoffel联络中，计算后得到：

将（2），（3）代入（5）式可得：

Ricci曲率张量为：

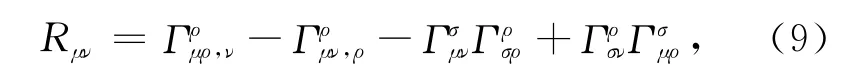
逆变Ricci曲率张量关于引力场hμν的一次展开式为：

根据（4）式，度规张量gμν关于引力场hμν的一次展开式即h（0）次项等于ημν.这样一来，曲率标量关于引力场hμν的最低次展开式即h（1）的项为：

根据（12）式，曲率标量R2关于引力场hμν最低次展开式，即h（2）次的项为

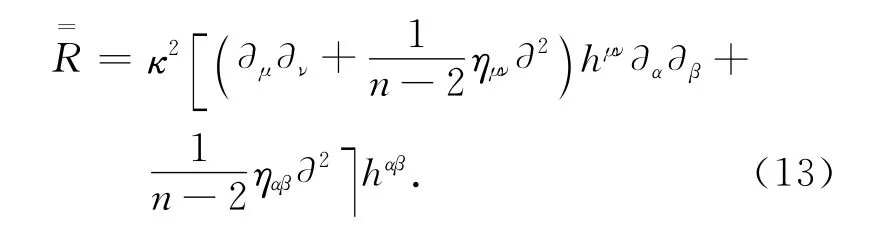
作用量S关于引力场hμν的最低次展开式，即h（1）的项为零.hμν的二次展开式即h（2）的项为

使用分部积分法，得到：

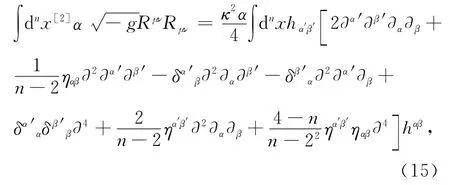
同理，可得：

下面计算（4）的三个积分项：

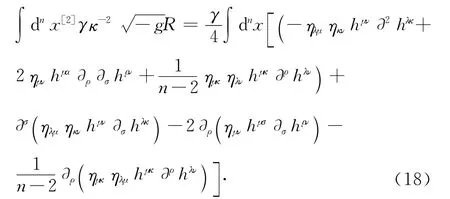
将（15）、（16）和（18）分别代入（3）中，R＋R2＋RμνRμν—引力的作用量关于引力场hμν的二次展开式为：

3 R＋R2＋RμνRμν—引力的量子化生成泛函

根据Fadeev－Popov方法，R＋R2＋RμνRμν—引力的量子化生成泛函由下列项构成：

在本文中

SFPG为Fadeev－Popov鬼粒子场作用量项.SE.S为作用量的外源项.本文采取下面的规范固定项：

其中Δ－1为规范参数.将SGF导入到生成泛函中，得到：

计算后得到规范固定项SGF用下式表示：

4 R＋R2＋RμνRμν—引力的自由传播子

引力的自由传播子，由作用量关于引力场hμν的微扰展开式中的二次项即h（2）的项贡献.有效作用量关于引力场hμν的微扰展开式中的二次项即h（2）用SFPG［2］表示，根据（19）和（25）有：

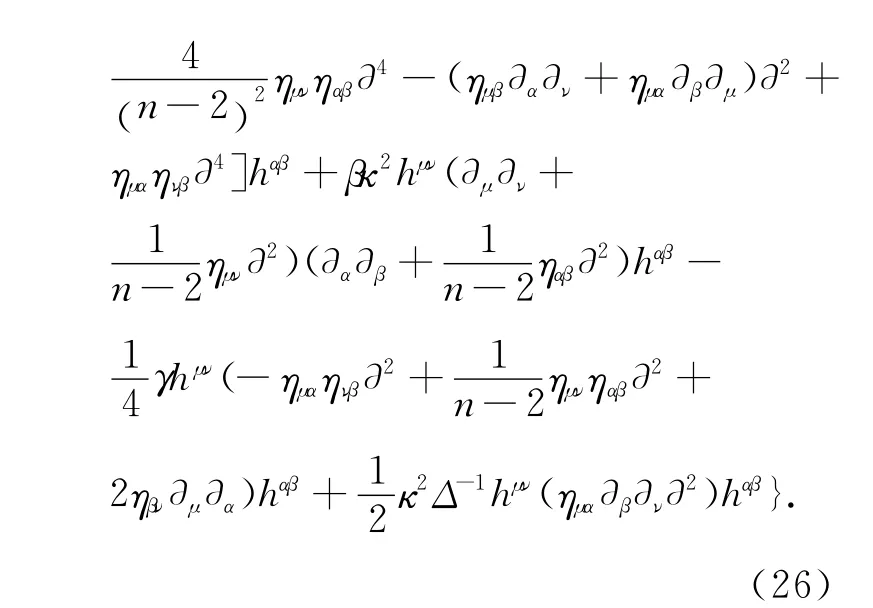
在树图近似下，正则顶点生成泛函等于有效作用量，即：

使用傅里叶变换，得到了动量表象中树图近似下正则顶点为：

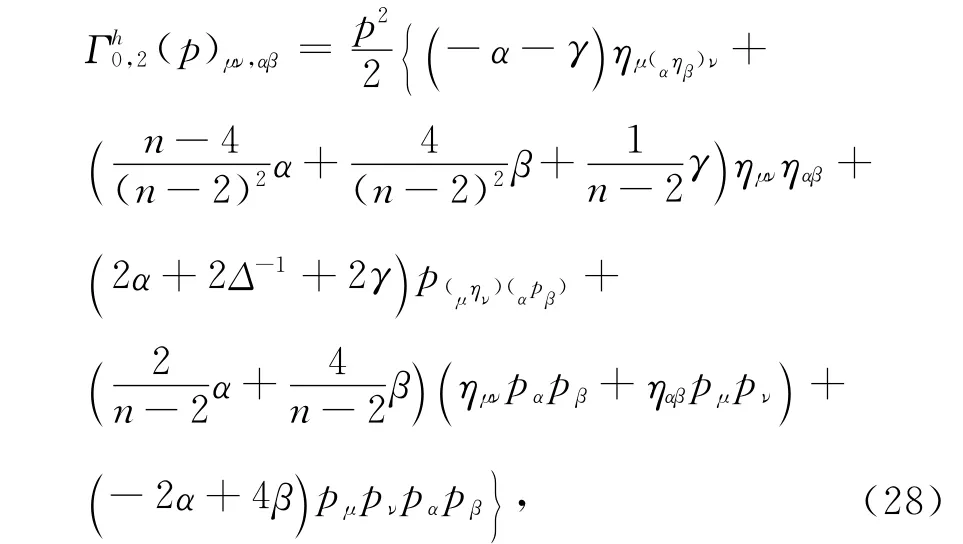
R＋R2＋RμνRμν－引力的引力子传播子由下列形式给出：

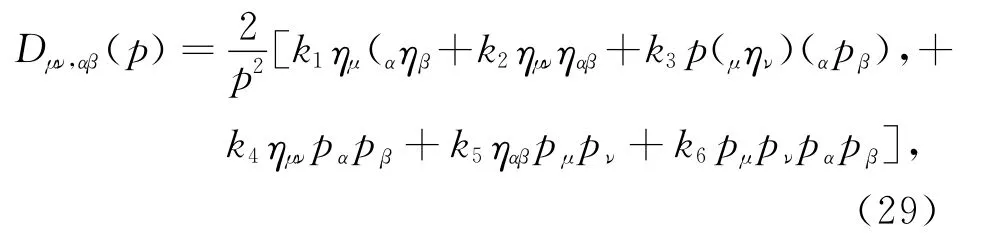
它和R＋R2＋RμνRμν引力的4－导数引力的引力子2点正则顶点Γh0，2（p）μν，αβ间存在倒数关系：

5 结论

通常在计算含引力子的自能圈图时，会产生重整化无法消除的发散，使计算过程无法进行下去.本文利用维数正规化方法，利用度规张量密度态的微扰展开，结合FaddeevPopov的量子化方法计算了携有高阶微分项的R＋R2＋RμνRμν的引力自由传播子.此种微扰法计算出来的结果发散固然存在，但在后续工作中，理论上可采用几何方法消除.文献［3］曾计算过引力场自由传播子，本文与其在原理上是一致的，不过，在具体计算技巧上有不同.本文的结果是直接用作用量中引力场hμν的直接表达式.这一结果计算明确，更便于同广义相对论量子化得到的结果进行比较.

［1］ Peskin M E，Schroeder V D.An Introdaction to Quantum Field Theory［M］.Beijing：World Publishing Crop，2006.

［2］ Battistel O A，Dallabona G.A systematization for one－loop 4D Feynman integrals［J］.Eur Phys J C，2006，45：721－743.

［3］ Stelle K S.Gauss－Bonnet type identity in Weyl－Cartan space［J］.Phys，1976，16：953－957.

［4］ Weinberg S.Gravitation and Cosmology［M］.New York：Wiley，1972.

［5］ Ryder L H.Quantum Field Theory［M］.Cambridge：Cambridge University Press，1985.

［6］ 邵 丹，邵 亮，邵常贵.一种空时体积与引力的激发和跃迁生成模式［J］.物理学报，2011，60：120401－120407.

［7］ 邵 丹，邵 亮，李 苗，等.五维时空中度规的计算［J］.物理学报，2010，59（06）：3700－3703.

［8］ 代 熠，明 钢.介质中的Minkowski动量的守恒［J］.华中师范大学学报：自然科学版，2011，42（2）：211－214.

［9］ 丁兆龙，邵 亮，韩金柱.非平坦时空中相对论性的玻色子和费米子［J］.华中师范大学学报：自然科学版，2008，42（2）：211－214.