凸轮轮廓曲线方程形式的探讨与研究*

邵世权，刘 霞

(菏泽技师学院，山东菏泽 274016)

0 引言

近年来，为了提高产品质量，提高劳动生产率，我国引进了许多国外先进的轻纺机械。这些进口设备的集成度高、结构紧凑、自动化程度高，代表了当今国际上最先进的专业设备水平［1］。为了尽量减少空间结构尺寸，设备上广泛采用了凸轮机构。在凸轮的反求中，求理论轮廓曲线是最关键也是最困难的一步。通过长时间研究凸轮总结了一种新的求解方法。

1 凸轮廓线求解的新思想

一般在求解凸轮廓线之前先要进行数据测量，进行测量数据处理之后，然后进行求解。那么用怎样的方法可快速的求解出符合从动件运动要求的廓线呢?在大量的工作中发现，如果把测量的数据先在绘图软件中初步进行样条拟合，这样既可发现奇异区，又可观察曲线的初步形状。如果有明显奇异点说明在该区间测量误差可能太大，必须进行重新测量或者采取新的测量手段。当没有奇异点时，可初步看出廓线的形状，这样就可初步决定对该曲线进行分段求解还是整体求解。

1.1 分段求解的判别条件

怎样判断出是否进行或者必须进行分段呢?笔者发现在绘图软件中初步拟合的曲线形状如果满足以下要求，即曲线斜率符号的变化次数如果大于曲线与任意一条水平线的交点个数，则必须进行分段求解。

“曲线斜率符号的变化次数如果大于曲线与任意一条水平线的交点个数”这句话的几何意义是无论我们怎样在xoy平面内平移曲线，该曲线与x轴的交点个数小于斜率符号变化的次数。如图1所示。

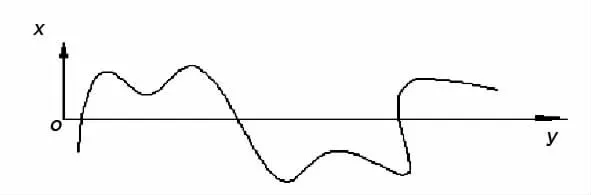
图1 特殊曲线图

图1中曲线的斜率符号变化有8次，而不管怎样移动曲线，曲线最多也只能与x轴的交点个数为6，小于8。不管怎样移动曲线与x轴的交点不可能超过8，即曲线方程最多只可能有6个根。即，不管怎样改曲线方程的常数项，方程根最多只能是6个。出现了根的个数小于斜率变化的次数，就像力学中的超静定问题一样，约束条件过多，无法仅用一个方程来表达整条曲线，必须进行分段。

一般情况是曲线斜率符号的变化次数如果大于曲线与任意一条水平线的交点个数，则必须进行分段求解。那么怎样分段呢?分段的原则是必须保证每段曲线至少与一条水平线交点的个数大于或者等于该段曲线斜率符号变化的次数。

1.2 分段后或不分段曲线方程形式的选择

函数形式的一般选择原则:如果曲线的斜率的符号有多次改变并且曲线形状较平缓，形状象波浪线或正弦线，那么一般不选择多项式，因为一般多项式在斜率频繁变化时很难保证曲线的平缓。这时就应该考虑正弦或余弦函数。如果曲线的斜率只有一次改变或者没有改变且曲线斜率值较大、变化快，则可以考虑多项式，这时用正弦或者余弦函数很难满足要求。初步选定函数的形式后就可进行曲线拟合，这可在Matlab中轻松实现。

如果样条的形状整体看起来是不光滑的，曲线的斜率有突变，在很小的区间内而引起曲率很大的变化甚至变号，那么就应该考虑对这样的曲线最好进行再分段拟合。再分段的原则是一般斜率突变的地方就是分段的地方，有几个突变区间就分几段。分段后，对每一段就可用上面的方法进行求解，各区间曲线用过渡函数进行过度［2］。

3 设计举例

某圆柱凸轮测量廓线的坐标如表1所列。

表1 凸轮坐标点测量

在电子图版中拟合样条的形状如图2所示。

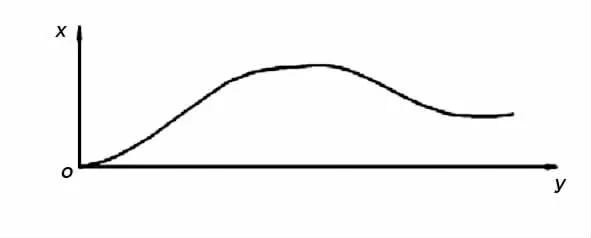
图2 样条曲线图

从样条中可看出，曲线的斜率发生了2次改变，而与水平线最多的交点个数为3，所以可用一个方程来表示曲线，又因为该曲线的形状平缓且形似正弦，所以选择正弦函数为拟合函数。采用最小二乘法解，根据表1中的数据可选择正弦函数［3］，设:

再把F值代入下式中，式中y表示测量值即凸轮上升的高度。

利用Matlab可计算出:

即所求的曲线方程为:

3 结语

在凸轮廓线反求中，由于曲线的形状变化多样，拟合函数也多样，给求解带来了很大困难。但如果按照上述的步骤，充分考虑曲线的斜率，就可使曲线拟合函数的形式大大缩小范围，也简化了计算过程。

［1］ 王福明，贺正辉，索 瑾.应用数值计算方法［M］.天津:科学出版社，1992.

［2］ 管荣法.凸轮与凸轮机构［M］.北京:国防工业出版社，1993.

［3］ 彭国勋.肖正扬.自动机械的凸轮机构设计［M］.北京:机械工业出版社，1990.

［4］ 王省富.样条函数及其应用［M］.西安:西北工业大学出版社，1989.