基于灵敏度分析的导管架海洋平台模型修正技术研究*

郭 琦，周国强，王维刚，陈文策，张晓勇

(1.东北石油大学机械科学与工程学院，黑龙江 大庆 163318; 2.东北石油大学秦皇岛分院井架检测国家计量认证重点实验室，河北秦皇岛 066004; 3.安徽马钢工程技术有限公司，安徽马鞍山 243000;4.抚顺石化公司，辽宁抚顺 113008)

0 引言

目前我国在役多年的导管架海洋平台很多，其结构本身都存在诸多未知的损伤缺陷，对平台进行检测和安全评估已经成为一个备受关注的课题。在平台的强度分析过程中，有限元模型的修正也是重要一环，综合有限元分析和实验静动力分析的模型修正方法式结构损伤和状态评估的有效方法，此方法是通过系统修正结构模型的建模误差、几何误差和物理特性误差来改进分析结果与实验测量结果之间的拟合程度［1－2］。根据修正对象的不同大致可分为矩阵型修正和参数型修正，其中参数型修正是对材料参数，截面形状，几何尺寸进行型修正且物理意义明确，是适合工程应用的一种模型修正方法［3－4］。对此国内外也有很多学者做了大量研究工作，且大都基于结构的动力信息对有限元模型进行修正，基于静力信息的很少，其原因是经历实验条件要求较高，故一直不太为人重视然而结构的静力识别却具有较高的精度与稳定性。Hajela和Soerio［5］对静力识别的前景保持乐观。邓苗毅等曾利用静载实验响应数据:挠度、转角和曲率以及结构分析计算得到的响应之差建立目标函数，通过序列二次规划计算法实现结构分段截面抗弯刚度识别。笔者基于我国海南陆丰13－1平台1: 50模型的静力应变数据探索一种提高有限元模型精度的一种方法。此模型材质为Q235A，模型在加工时由于加工工艺和精度等限制不可避免存在缺陷，因此实测的静力应变数据与理想化有限元模型所计算出的数据会存在一定误差。利用实测的静力应变信息对导管架模型有限元模型进行参数修正。通过迭代过程使得分析应变和实验应变的误差在给定的收敛边界内达到最小称为有限元模型修正技术。根据实测的静力应变数据，采用基于应变残差灵敏度优化设计方法对实验室导管架平台模型进行有限元模型修正。

1 灵敏度分析

灵敏度分析是工程研究中一个很重要而又能构获得良好效益的领域，因而获得了广泛的应用［6－7］。对于八腿导管架海洋平台这类非常复杂的钢结构，静力应变数据通过实验比较容易获得，且识别精度高，所以现在主要从结构的静力应变对物理参数变化的灵敏度出发来进行研究。

结构的损伤可以看做是结构物理参数的一个摄动。为了确定结构物理参数的变化对结构测点处应变的影响，即在结构物理参数有一个摄动时，引起测点应变变化，因此有必要进行应变残差灵敏度分析。把结构的损伤(如局部刚度的降低)视作结构参数的变化，进行结构的灵敏度分析可以看出结构的哪些杆件的损伤对测点处应变影响更大。

按照有限元理论，单元节点应变与节点力之间的关系为:

式中:Pi为节点力;Ki为单元刚度矩阵;Ui为节点位移。

εi和Bi为节点应变和几何函数矩阵。

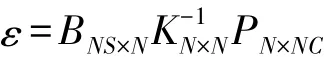
其中有NS个测点和NC个线性无关工况。原计算模型的分析结果与实测值的残差:

残差矩阵eε对各参数求偏导便得到了应变残差灵敏度矩阵:

2 有限元修正方法

利用模型修正的方法进行结构损伤识别时面临的关键问题包括:①修正参数选择;②目标函数的确定;③优化方法等。下面针对这几个问题来分析导管架结构的有限元修正问题。

2.1 修正参数的选择

在修正过程中，修正参数的选择是至关重要的。有限元模型的不精确因素主要来自三个方面:模型结构的误差、模型阶次的误差和模型参数的误差。假定模型参数的误差是有限元误差的主要因素。模型参数误差一般有不精确的材料、几何参数和连结、边界条件估计引起。修正导管架结构有限元模型参数时，假定连接部位都为刚性连结，为了合理的选择修正参数、提高修正效率，修正参数的选择主要通过灵敏度分析实现。导管架结构复杂杆件繁多，通过灵敏度分析选取高灵敏度杆件的有效壁厚和弹性模量为修正参数。

约束优化原理:结构的有限元模型修正问题可以转变成为结构参数的优化问题。有限元元模型的修正过程可以利用结构的实测静力特性(应变)进行参数优化的过程。可以用数学模型描述如下:

式中:f为目标函数;x为设计变量;gihj为状态变量; l，m为约束条件个数。

使用一阶优化算法将有约束多变量规划问题转化成无约束规划问题，即将元目标函数f(x)增加最函数转化为新函数

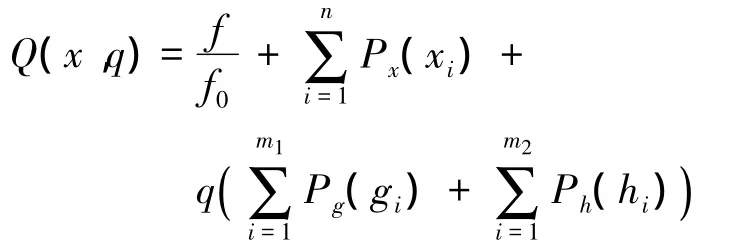
式中:f0为参考目标函数，q为控制约束参数，px为设计变量外罚函数，pg和ph为状态变量混合罚函数。

收敛准则:迭代修正的收敛准则定义为:

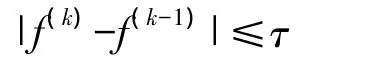
式中:f(k)为第k步迭代后的目标函数;f(k－1)为第k－1次迭代后的目标函数。本文取:

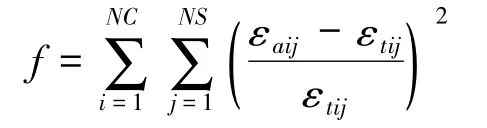
式中:eaij为计算应变;εtij为实测应变;i为工况号;j为片号。

当满足收敛条件时收敛结束，如不满足收敛条件则得到一个新的搜索方向，进行下一轮迭代计算，直至收敛。实验室导管架的静力实验应变分析。

2.2 实验室导管架模型

导管架平台模型为南海陆丰13－1平台以1:50比例，材料为Q235A。使用美国BDI STS－WiFi无线结构测试系统对平台进行应变测试，布片位置见图1黑色箭头位置。井口压力2.5 kN、5.05 kN、6.75 kN、10.87 kN、14.50 kN、18.91 kN，其中14.50 kN和18.91 kN为验证载荷，其余为修正载荷。

2.3 有限元分析

构造有限元模型如图2所示。

图1 实验装置图

图2 有限元模型

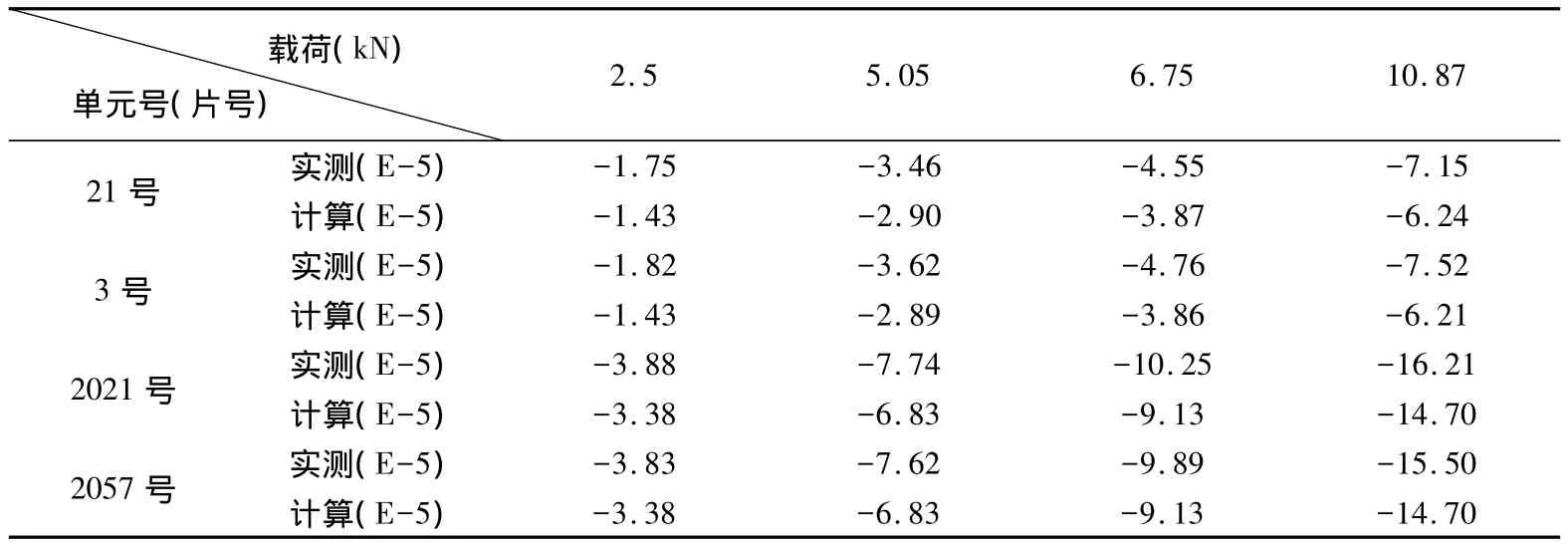
表1 实验前实验与计算应变结果

表2 实验室导管架修正前、后的参数值及其变化

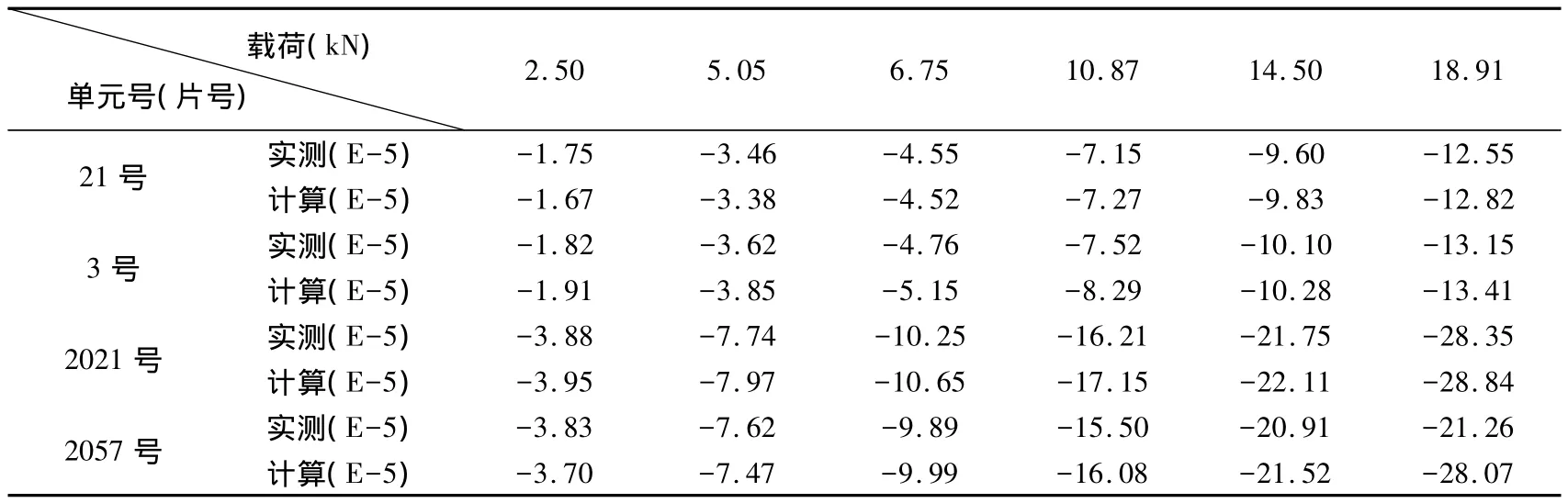
表3 修正后实测应变与计算应变对比

结构所有单元由beam188单元，每个节点6个自由度。每根桩腿和斜支撑都单独付截面参数并划分网格。桩腿下端固结于基底，采用全约束。构造的有限元模型具有2 192个单元，1 734个节点，10 356个自由度。用Ansys进行静力分析，表1为实验所得应变数据。

3 有限元模型修正

鉴于导管架平台模型结构复杂杆件繁多，且在初步的有限元分析后发现横向支撑受力不大，应力分布较均匀，而且Ansys所容许设计变量个数(20个以内效率较高)限制，此研究以每根桩腿、每层斜支撑的有效壁厚、所有横向支撑的有效壁厚和所有杆件的弹性模量为参数初选出待修正参数47个，通过灵敏度分析后选取了其中19个高灵敏度参数，这些参数为此工况下主要承载杆件的有效壁厚和弹性模量。其初始估计值与修正后变化见表2。(表2中DI1、DI5、DO1为最外侧三根最粗桩腿下段部分的内径，DO3、DO5、DO7为最外侧三根最粗桩腿中段段部分的内径，Ds2、Ds6、Ds7、Ds8为最外侧三根最粗桩腿中段段部分的内径，DO10、DO11、DO15、Dh1为中间四根较细桩腿的中、下段内径，Dh6、Dh8、Dh12、Ds1为中间四根较细桩腿的上段内径)。

优化迭代收敛后最大相对误差10.24%，最小相对误差0.7%，各工况下个测点计算应变与实测应变对比见表3(表3中14.5kN和18.91kN为检验工况)，检验况工下各测点最大相对误差32.03%，最小相对误差1.35%。

4 结语

基于结构静力应变对物理参数的灵敏度，探讨了以设计参数型修正方法为基础的导管架海洋平台有限元模型修正技术的可行性，为在役导管架海洋平台的损伤识别和状态评估提一种方法。

采用基于应变残差灵敏度分析的优化设计方法，以实验室导管架海洋平台模型实测静力应变分析结果为依据，对建立的理想有限元模型进行优化修正。结果显示该方法可以较好的修正初始建立的有限元模型修正后其最大误差32.03%最小误差1.35%，使得有限元模型更好的接近实际结构，反应导管架结构的真是状态和实际的工作性能，从而为在役导管架海洋平台的检测和安全评估提供更加准确的有限元模型。

［1］ 李慧彬，郑朝昌.对国内外桥梁损伤诊断的集中方法的评述［J］.工程力学，1998(3):407－414.

［2］ 李华军，杨和振.海洋平台结构参数识别的诊断技术的研究进展－第十三届全国结构.工程学术会议特邀报告［J］.工程力学2004 21(1):114－138.

［3］ 张德文，魏阜旋.模型修正与破损诊断［M］.北京:科学出版社，1999.

［4］ 淳 庆，邱洪兴.钢桁梁桥基于模型修正方法的损伤程度识别研究［J］.地震工程与工程震动，2005，25(2):114－118.

［5］ Hajela P，F J.Recent Developments in Damage Detection Based on System Identification Methods［J］.Structural Optimization，1990 (2):1－10.

［6］ 郭 彤，李爱群，韩大章.基于灵敏度分析与优化原理的大跨桥梁动力模型修正［J］.桥梁建设，2004(6):20－23.

［7］ 范立础，袁万城，张启伟.悬索桥结构基于敏感性分析的动力有限元模型修正［J］.土木工程学报，2000，33(1):9－14.