改进的PTM方法及其在区间估计中的应用

吕 鹏,相荣霞,袁永生

(河海大学 理学院,江苏 南京 210098)

PTM(投影深度削减平均)[1]方法是一种比较稳健的区间估计方法，该方法基于Bootstrap抽样[2-7]，合理地引进深度函数[1,4-5]，抑制异常点[6]、重尾分布以及污染数据的影响.但是，从文献[8-9]提出的PTM方法虽然具有较好的稳健性，但按照深度截尾得到的区间偏左，或可能出现区间“倒置”，而且在小样本情形下，运用该方法可能存在溢出，因此不可用.基于上述可能存在的缺陷，笔者合理地改进了PTM方法，对原来的深度函数进行重新定义,得到了更加合理的，既适合于小样本情形，又适合于大样本情形下的再抽样区间估计方法.

1 Bootstrap抽样方法

Bootstrap实际上就是一种再抽样方法，再抽样的次数通常很大，一般都在200次以上.本文用到2种Bootstrap抽样方法[2,7].

方法1 直接利用原始样本数据作有放回抽样.设从1～n内产生的n个随机整数，以上述随机产生数为下标的原始样本数据作为再生样本.这种方法可能存在如下2个缺点：

1) 抽样后所产生新的样本序列可能并不服从原始样本所服从的总体分布.

2) 抽样之后的样本总体依赖于(0，n)随机发生器，若(0，n)随机发生器产生的数据服从某种分布或者均衡性不好，会使最终的抽样总体存在系统偏差.当然这个问题可以解决.

设原始样本为x1,x2,…,xn，在(0,1)内随机产生n个(0,1)内的小数ri,i=1,2,…,n，其中n为原始样本容量.令αi=(n-1)ri，βi=|αi|+1，i=1,2,…,n，并且令y*i=xβi+(βi-αi+1)(xβi+1-xβi)，i=1,2,…,n，以此作为一个新的样本.如此继续重复抽样B次，得到B个Bootstrap样本[2].

2 改进的PTM方法

对PTM方法进行改进，对原来的深度函数进行重新定义,利用深度函数的大小来去掉原始数据中的异常点, 使得到的参数估计的置信区间更加精确地逼近于真值，从而提高区间估计的精度.

改进的PTM方法的一般步骤.

第1步：定义PTM.

1) 设X=(x1,x2,…,xn)为任意样本，令Med(X)为样本中位数，MAD(X)为{|xi-Med(X)|,(i=1,2,…,n)}的中位数.

2) 定义深度函数

对原来的深度函数进行重新定义，可以克服原来定义中的可能出现溢出的缺陷，使得到的改进的PTM方法更加合理有效.

3) 对于某一个常数β>0，对于所有满足PD(xi,X)≥β的xi(i=1,2,…，k)有

其中，之所以取某一个常数β>0，并对所有满足条件PD(xi,X)≥β的xi取均值，作为均值参数μ的一个估计，其主要思想是利用深度函数的大小来去掉原始数据中的异常点或者“贡献”较小点的影响，使得到的参数估计的置信区间更加精确地逼近于真值或者在样本均值附近，从而提高区间估计的精度.并且可以证明PTMβ(X)渐近趋于均值μ.

第2步：利用Bootstrap抽样方法，得到参数的估计区间：

1) 设X=(x1,x2,…,xn)为来自于经验分布Fn的样本容量为n的任意样本，采用Bootstrap抽样方法，对这组样本进行模拟抽样，得到B组样本容量为n的样本，我们把这B组样本放在一起，记作Y=(X1,X2,…,XB)；

2) 对这B个样本中的每一组样本，分别按照PTM的定义进行计算，得到B个PTMβ值，按照样本下标顺序，我们令得到的PTMβ值分别为

PTMβ1,PTMβ2,…,PTMβB;

3)然后将PTMβ1,PTMβ2,…,PTMβB按照大小排序PTMβ(1),PTMβ(2),…,PTMβ(B)；

将得到的PTMβ1,PTMβ2,…,PTMβB按照大小进行排序，改变了原来PTM方法中按照深度进行排序，这样主要是避免出现置信区间“倒置”的缺陷.

4) 对于给定的精度α，利用百分位法截尾，得到的置信区间为

(PTMβ(⎣B.α/2⎤+1),PTMβ(⎣B.(1-α/2)⎤)).

3 改进的PTM方法的优良性比较

改进的PTM方法是基于左义君PTM方法的优势[8-9]，结合其存在的缺陷，加以改进得到的一种合理的、有效的、稳健的区间估计方法.该方法可以适用于任何分布的指定参数的区间估计.下面本文分别在正态分布、泊松分布、指数分布的情形下，分别基于小样本情形和大样本情形，比较改进的PTM方法和经典方法、百分位法的优良性.

用Matlab软件和数据模拟的方法比较改进的PTM方法与经典t方法、百分位法，以此来研究改进的PTM方法的优良性.

由于本文中Bootstrap抽样方法有2种，且使用较多的是方法1(称为一般的Bootstrap抽样方法)和方法2(称为加权处理的Bootstrap抽样方法[2,10]).因此，基于不同的Bootstrap抽样方法，比较改进的PTM方法和传统方法的优良性.并且在样本容量不同时，各种方法表现出来的优良性也不相同，结合有关样本数目的规定，分别比较当样本容量为7、20、和120，Bootstrap抽样为500时的改进的PTM的优良性.见表1～2.

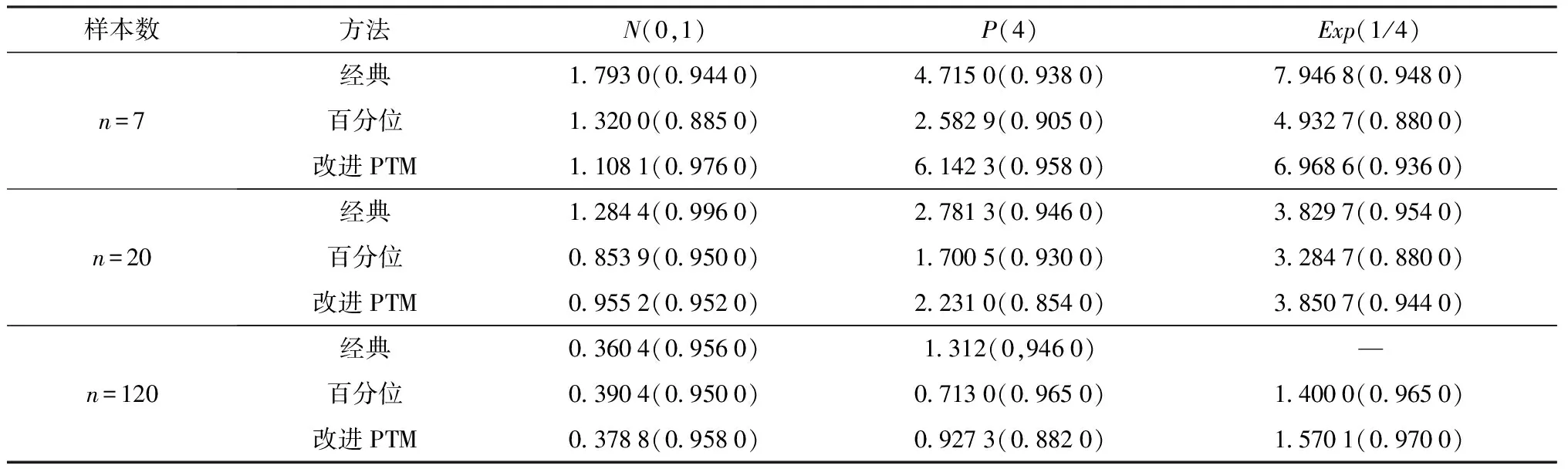
表1 一般Bootstrap抽样下置信水平为95%的随机模拟500次置信区间的平均长度(覆盖率)

表2 加权Bootstrap抽样下置信水平为95%的随机模拟500次置信区间的平均长度(覆盖率)

1)n=7时，改进的PTM方法中的参数β的取值在不同的分布下取不同的值，一般的在正态分布下，令β=0.52，在泊松分布下，令β=0.5，在指数分布下，令β=0.53.N=20，120时，PTM方法中，参数β的取值均取值为0.5.

2) 在实际的问题当中，当样本容量小于15时，经典方法是不适用.在这里我们暂时假设它可以适用，比较得到上述结果.

综合上述多种情形可以看出：在总体为正态分布和指数分布时，改进的PTM都具有较好的优良性.特别是在小样本的情形下，改进的PTM方法较经典方法和百分位法具有更好的优良性：相同置信水平下，较经典方法得到的置信区间平均长度更短，并且真值的覆盖率较高，基本处于95%左右.对于加权处理的 Bootstrap 抽样方法，在相同置信水平下，改进 PTM 方法得到的置信区间平均长度更短，且具有更好的稳健性.在总体分布为泊松分布时，改进的PTM方法的优良性不突出，可能跟泊松分布样本的离散性有关，需要进一步的验证分析.

4 实例验证

数据来自某厂某种灯泡的寿命[11]，已知服从正态分布，现从一批灯泡中随机抽取16个，测得其寿命为 1 510、1 450、1 480、1 460、1 520、1 480、1 490、1 460、1 480、1 510、1 530、1 470、1 500、1 520、1 510、1 470 h.

从表3中可以看出在小样本情况下，一般Bootstrap抽样下的PTM方法所得的所有灯泡的平均寿命的置信区间比用 Bootstrap 4 种方法和常规方法估计的区间宽度短，从而说明对于一般的 Bootstrap 抽样方法，在相同置信水平下，改进 PTM 方法得到的置信区间平均长度更短，且具有更好的稳健性.同时，加权Bootstrap抽样下的PTM方法所得的所有灯泡的平均寿命的置信区间比一般Bootstrap抽样下的PTM方法所得的所有灯泡的平均寿命的置信区间的区间宽度要更小一点，具有更高的精度.

表3 常规方法和 Bootstrap 方法以及PTM方法对灯泡寿命的区间估计

注：PTM1为一般Bootstrap抽样下的PTM方法，PTM2为加权Bootstrap抽样下的PTM方法；上述Bootstrap抽样次数B均为1000.

在小样本情形下，改进的PTM方法较经典方法具有更高的精度，相同置信水平下，改进的PTM方法得到的置信区间平均长度更短，且具有较高的真值覆盖率，所以改进的 PTM 方法得到的置信区间具有较好的稳健性;尤其在加权之后的 Bootstrap 方法下，所得到的区间更加稳健，左右摆动的幅度更小，且区间长度更短.

参考文献:

[1] ZUO Yi-jun.Data depth trimming counterpart of the classicalt(orT2) procedure[J].Journal of Probability and Statistics, 2009(2009):1-9.

[2] 张守玉,封伟书.基于Bootstrap方法的正态分布样本数据生成研究[J].装配指挥技术学院学报,2009,20(2):97-100.

[3] 扎库拉.戈文达拉玉卢.抽样理论与方法(英文版)[M].北京:机械工业出版,2005:324-333.

[4] 李强.两类数据深度及深度加权M估计[D].长沙:国防科学技术大学,2008:10-20.

[5] 范允征,林路.稳健的深度加权小波估计[J].南通大学学报:自然科学版,2008,7(4):78-81.

[7] 吴昌莉.小子样样本均值区间估计方法及其比较[C]//第七届全国核仪器及其应用学术会议暨全国第五届核反应堆用核仪器学术会议论文集.北京市:中国电子学会核电子学与核探测技术分会,2009：37-40.

[8] LIU Xiao-hui, ZUO Yi-jun.Computing projection depth and its associated estimators[M].New York: Springer Science, 2012.

[9] ZUO Yi-jun.A note on finite sample breakdown points of projection dased multivariate location and scatter statistics[J].Metrika,2000,(51):259-265

[10] BRADLEY EFRON.Better Bootstrap confidence intervals[J].Journal of American Statistical Association,1987,82(97):171-185.

[11] 赵慧琴.Bootstrap 方法在区间估计中的应用[J].江西科学,2010, 4:429-431.